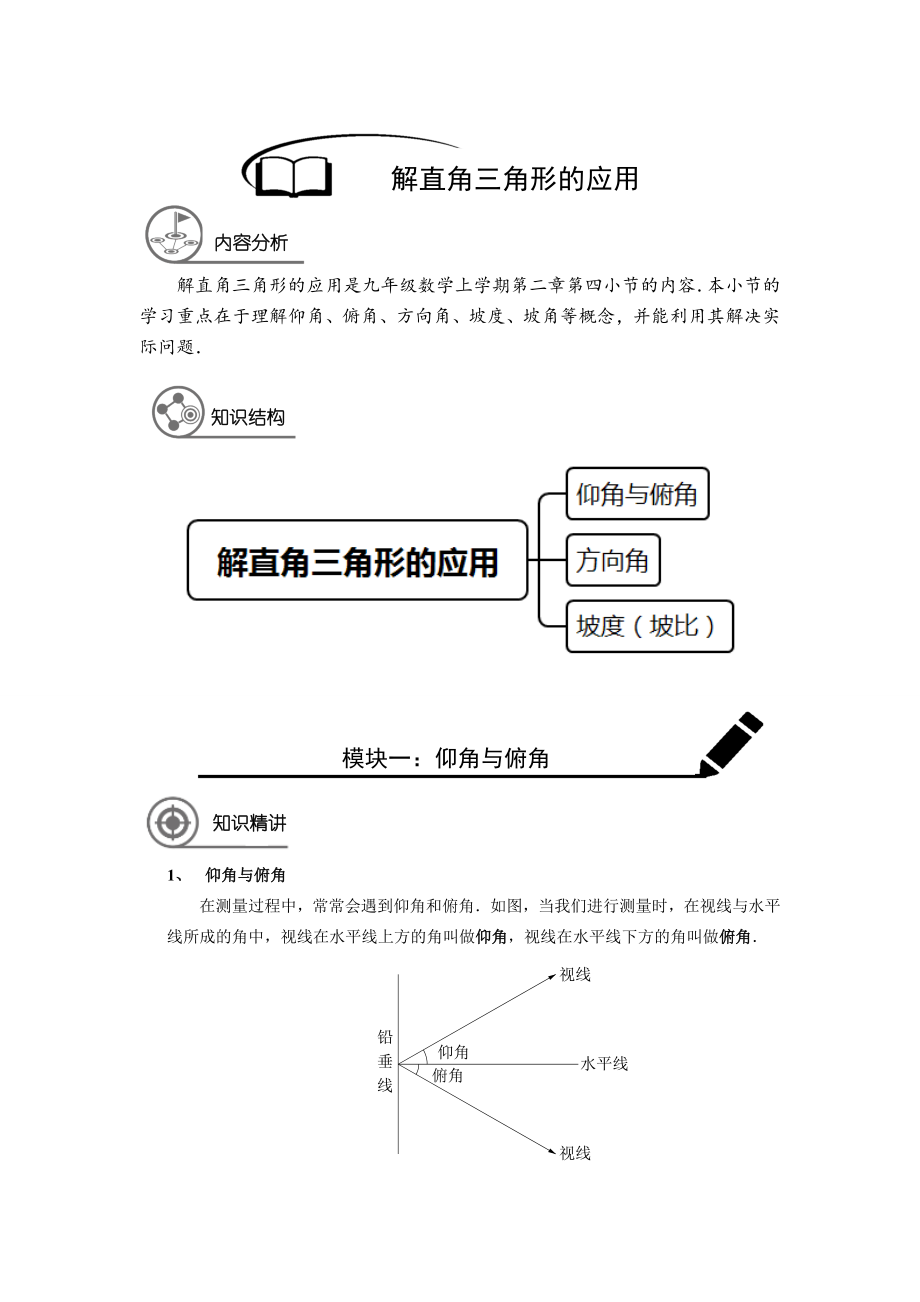
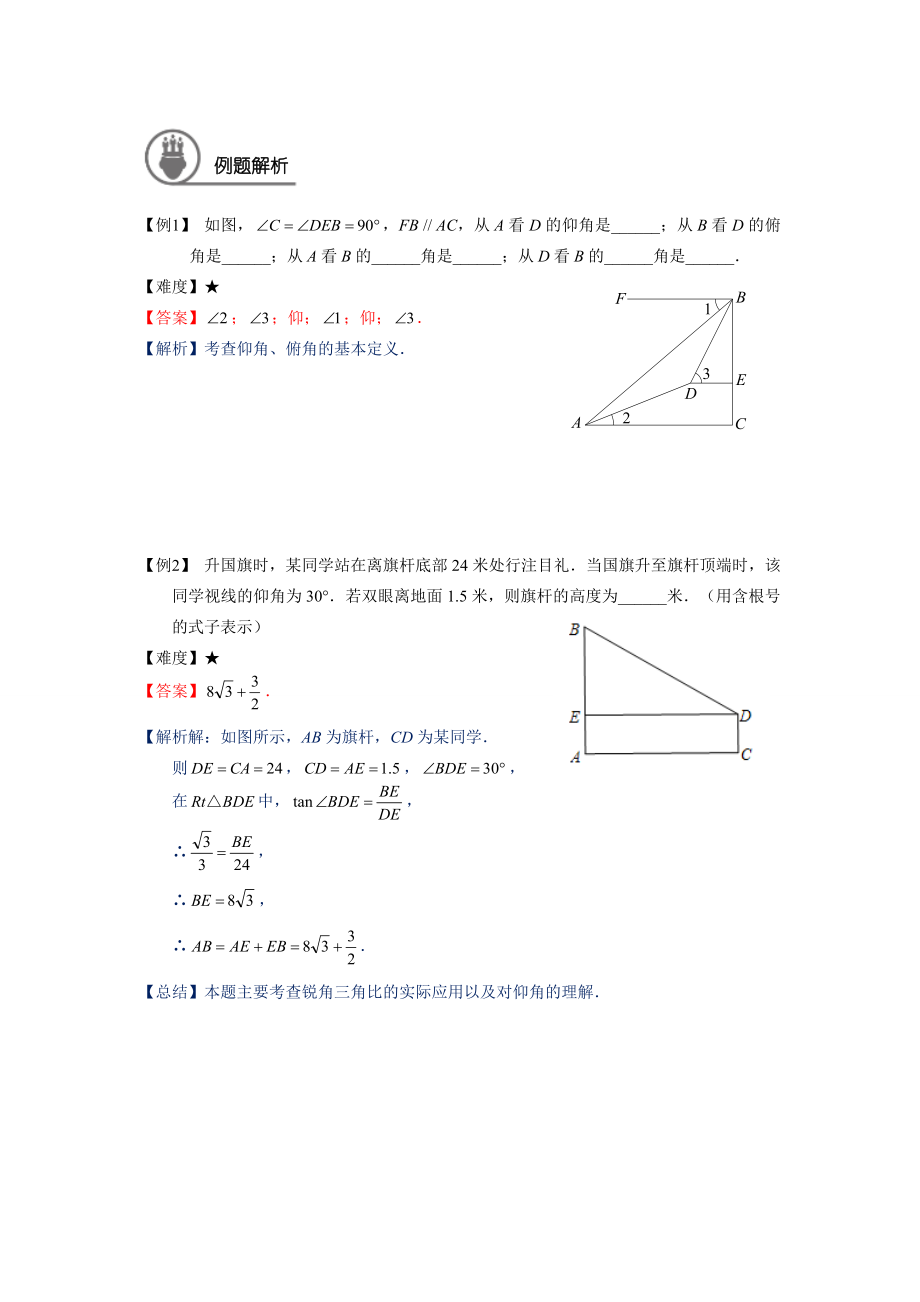
1、解直角三角形的应用内容分析解直角三角形的应用是九年级数学上学期第二章第四小节的内容本小节的学习重点在于理解仰角、俯角、方向角、坡度、坡角等概念，并能利用其解决实际问题知识结构模块一：仰角与俯角知识精讲1、 仰角与俯角在测量过程中，常常会遇到仰角和俯角如图，当我们进行测量时，在视线与水平线所成的角中，视线在水平线上方的角叫做仰角，视线在水平线下方的角叫做俯角仰角视线水平线视线俯角铅垂线例题解析【例1】 如图，FB / AC，从A看D的仰角是_；从B看D的俯角是_；从A看B的_角是_；从D看B的_角是_ABCDEF123【难度】【答案】；仰；仰；【解析】考查仰角、俯角的基本定义【例2】 升国旗时，
2、某同学站在离旗杆底部24米处行注目礼当国旗升至旗杆顶端时，该同学视线的仰角为30若双眼离地面1.5米，则旗杆的高度为_米（用含根号的式子表示）【难度】【答案】【解析解：如图所示，AB为旗杆，CD为某同学则，在中，【总结】本题主要考查锐角三角比的实际应用以及对仰角的理解【例3】 如图，两建筑物水平距离为a米，从点A测得点C的俯角为，测得点D的俯角为，则较低建筑物CD的高为（）Aa米B（）米C米D米ABCDE【难度】【答案】D【解析】过C作CEAB，垂足为E由题意有：，在中，在中，【总结】本题主要考查锐角三角比的实际应用以及对俯角的理解【例4】 如图，河对岸有一座铁塔AB，若在河这边C、D处分别用
3、测角仪器测得顶部A的仰角为30、45，已知CD = 30米，求铁塔的高（结果保留根号）【难度】ABCD【答案】【解析】解：由题意可得：，设，则，在中，解得：【总结】本题主要考查锐角三角比的实际应用以及对仰角的理解【例5】 如图，热气球的探测器显示，从热气球看一栋高楼顶部的仰角为60，看这栋高楼底部的俯角为30，热气球与高楼的水平距离为120m，请问：这栋高楼有多高？（结果精确到0.1m）ABCD【难度】【答案】277.1米【解析】解：由题意可得：，在中，在中， 【总结】本题主要考查锐角三角比的实际应用以及对仰角、俯角的理解和运用【例6】 如图，某幢大楼顶部有一块广告牌CD，甲、乙两人分别在相距
4、8米的A、B两处测得点D和点C的仰角为45和60，且A、B、E三点在一条直线上，若BE = 15米，求这块广告牌的高度（取，计算结果保留整数）ABCDE【难度】【答案】3【解析】解：由题意可得：，在中，在中， 【总结】本题主要考查锐角三角比的实际应用以及对仰角的理解和运用【例7】 某高层建筑物图中AB所示，小明家住在高层建筑物附近的“祥和”大厦（图中CD所示），小明想利用所学的有关知识测量出高层建筑物AB的高度他先在自己家的阳台（图中的Q点）测得AB的顶端（点A）的仰角为37，然后来到楼下，由于附近建筑物影响测量，小明向AB方向走了84米，来到另一座高楼的底端（图中的点P处），测得点A的仰角为
5、45已知点C、P、B在一条直线上，小明家的阳台距地面60米，请你画出示意图，并根据上述信息求出AB的高度ABCDPQE（参考数据：，）【难度】【答案】492米【解析】过Q作AEAB，垂足为E解：由题意可得：，设，则在中，【总结】本题综合性较强，需要认真分析题目中的条件，然后利用锐角三角比解决实际问题【例8】 如图，为某小区的两幢10层住宅楼，由地面向上依次为第1层、第2层、第10层，每层的高度为3米，两楼间的距离AC = 30米现需了解在某一时间段内，甲楼对乙楼采光的影响情况假设某一时刻甲楼楼顶B落在乙楼的影子长EC = h，太阳光线与水平线的夹角为（1）用含的式子表示h；（2）当= 30时，
6、甲楼楼顶B的影子落在乙楼的第几层？从此时算起，若每小时增加10，约几小时后，甲楼的影子刚好不影响乙楼采光（结果精确到0.01）ABCD甲楼乙楼太阳光EF【难度】【答案】(1)；（2）第4层，6小时【解析】解：(1)由题意可得：过E作FEAB，垂足为F在中， （2）如图2，若每小时增加10，需要1.5小时才能从30到90【总结】本题综合性较强，需要认真分析题目中的条件，然后利用锐角三角比解决实际问题模块二：方向角知识精讲1、 方向角指北或指南方向线与目标方向线所成的小于90的角叫做方向角如图：北偏东30，北偏西70，南偏东50，南偏西45北北偏东30南偏西45北偏西70南偏东5030704550
7、例题解析【例9】 如果由点A测得点B在北偏东15的方向，则由B测点A的方向为（ ）A北偏东15B北偏西75C南偏西15D南偏东75【难度】【答案】B【解析】考查方向角的定义ABC东南西北D【例10】 如图，小明从A地沿北偏东30方向走米到B地，再从B地向正南方向走200米到C地，此时小明离A地_米【难度】【答案】100【解析】解：由题意可知：在中，【总结】本题主要考查对方位角的准确理解和运用【例11】 如图，一艘轮船由海平面上A地出发向南偏西40的方向行驶40海里到达B地，再由B地向北偏西20的方向行驶40海里到达C地，则A、C两地相距（ ）A30海里B40海里北北ABCC50海里D60海里【
8、难度】【答案】B【解析】解：，为等边三角形【总结】本题主要考查利用方位角解决实际问题【例12】 在位于O处某海防哨所的北偏东60相距6海里的A处，有一艘快艇正向正南方向航行，经过一段时间快艇到达哨所东南方向的B处，则A、B间的距离是_海里（精确到0.1海里，）【难度】【答案】5.5【解析】解：由题意可知：，在中，【总结】本题主要考查利用方位角解决实际问题【例13】 如图，一艘海轮位于灯塔P的北偏东65方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东34方向上的B处，请问，此时，海轮所在的B处距离灯塔P有多远？（精确到0.01海里，）东南西北ABPC【难度】【答案
9、】130.23【解析】解：在中，在中，【总结】本题主要考查利用方位角解决实际问题ABC东北D【例14】 如图，A、B为湖滨的两个景点，C为湖心一个景点景点B在景点C的正东方向，从景点A看，景点B在北偏东75方向，景点C在北偏东30方向一游客自景点A驾船以20米/分的速度行驶了10分到达景点C，之后又以同样的速度驶向景点B，该游客从景点C到景点B需用多长时间？（，精确到1分）【难度】【答案】27分【解析】过A作ADBC的延长线于D由题意可得：，在中，在中，【总结】本题主要考查利用方位角解决实际问题【例15】 如图，某船以36海里/时的速度向正东方向航行，在点A测得某岛C在北偏东60方向上，航行半
10、小时后到达点B，测得该岛在北偏东30方向上，已知该岛周围16海里内有暗礁（1）试说明点B是否在暗礁区域外？（2）若继续向东航行有无触礁危险？请说明理由东北ABCD【难度】【答案】（1）B在暗礁区外；（2）有危险【解析】解：（1）由题意可得：，B在暗礁区外（2）在中，若继续向东航行有触礁危险【总结】本题主要考查利用方位角解决实际问题，注意在触礁问题中的最小距离指的是垂直距离【例16】 如图，AC是某市环城路的一段，AE、BF、CD都是南北方向的街道，其与环城路AC的交叉路口分别是A、B、C经测量，花卉世界D位于点A的北偏东45方向、点B的北偏东30方向上，AB = 2千米，ABCDEF环 城 路
11、和平路文化路中山路G（1）求B、D之间的距离；（2）求C、D之间的距离【难度】【答案】（1）2；（2）【解析】解：(1)由题意得：，(2)过C作CGBD，垂足为G在中，【总结】本题主要考查利用方位角解决实际问题，要注意认真分析题意【例17】 如图，甲、乙两只捕捞船同时从A港出海捕鱼，甲船以每小时千米的速度沿北偏西60的方向前进，乙船以每小时15千米的速度沿东北方向前进，甲船航行2小时到达C处，此时甲船发现渔具丢在乙船上，于是甲船加快速度（匀速）沿北偏东75的方向追赶，结果两船在B处相遇（1） 甲船从C处追赶上乙船用了多少时间？（2） 求甲船加快速度后，追赶乙船时的速度？（结果保留根号）东北东北
12、ABCD【难度】【答案】（1）4小时；（2）【解析】解：由题意可得：， ， 在中， ， ， ， （1）；（2）【总结】本题主要考查利用方位角解决实际问题，要注意认真分析题意【例18】 如图，在航线l的两侧分别有观测点A和B，点A到航线l的距离为2千米，点B位于点A北偏东60方向且与点A相距10千米处现有一艘轮船从位于点B南偏西76方向的C处，正沿该航线自西向东航行，5分钟后该轮船行至点A正北方向的点D处（1）求观测点B到航线l的距离；（2）求该轮船航行的速度（结果精确到0.1千米/时）ABCDEl东北FH（参考数据：，）【难度】【答案】（1）3；（2）40.4【解析】解：（1）由题意有：，在中
13、，(2)在中，【总结】本题主要考查利用方位角解决实际问题，要注意认真分析题目中给出的条件模块三：坡度（坡比）知识精讲1、 坡度（坡比）、坡角 在修路、挖河、开渠等设计图纸上，都需要注明斜坡的倾斜程度如图，坡面的铅垂高度h和水平宽度l的比叫做坡面的坡度（或坡比），记作i，即hl坡度通常写成1 : m的形式，如坡面与水平面的夹角叫做坡角，记作坡度i与坡角之间的关系：例题解析【例19】 某人沿着坡度为3 : 4的斜坡前进了10米，则他所在的位置比原来的位置升高_米【难度】【答案】6【解析】考查坡度的定义【例20】 某铁路路基的横断面是等腰梯形，其上底为10米，下底为13.6米，高1.2米，则腰面坡角
14、的正切值为_【难度】【答案】【解析】考查等腰梯形双高的辅助线【例21】 如图，坡角为30的斜坡上两树间的水平距离AC为2米，则两树间的坡面距离AB为（ ）ABCA4米B米C米D米【难度】【答案】C【解析】考查坡角的定义【例22】 如图，燕尾槽的横断面中，槽口的形状是等腰梯形，其外口宽AD = 15毫米，槽的深度为12毫米，的正切值为，则它的里口宽BC = _ABCD【难度】【答案】33毫米【解析】考查等腰梯形双高的辅助线【例23】 河堤横断面是梯形，上底为4米，堤高为6米，斜坡AD的坡度为1 : 3，斜坡CB的坡角为45，则河堤横断面的面积为_平方米【难度】【答案】96【解析】考查坡角的基本定
15、义【例24】 如图，一个大坝的横断面是一个梯形ABCD，其中坝顶AB = 3米，经测量背水坡AD = 20米，坝高10米，迎水坡BC的坡度i = 1 : 0.6，求迎水坡BC的坡角的余切值和坝底宽CDABCDEF【难度】【答案】；【解析】过A、B作AECD，BFCD由题意可得：，在中，在中，【总结】本题主要考查坡脚和坡比的概念【例25】 如图，某村开挖一条长1600米的水渠，渠道的横断面为等腰梯形，渠道深0.8米，下底宽1.2米，坡度为1 : 1求一共挖土多少立方米？ABCD【难度】【答案】2560【解析】，【总结】考查等腰梯形双高辅助线的做法和坡度的基本定义ABCDEF【例26】 如图，小杰
16、发现垂直地面的旗杆AB的影子落在地面和斜坡上，影长分别为BC和CD，经测量得BC=10米，CD=10米，斜坡CD的坡度为，且此时测得垂直于地面的1米长标杆在地面上影长为2米，求旗杆AB的长度 （答案保留整数，其中）【难度】【答案】13【解析】解：延长AD和BC交于点E，过D作DFBE由题意可知：，在中，设，则，在中，在中，【总结】本题主要考查利用坡脚和坡比的概念以及锐角三角比的相关概念解决实际问题【例27】 如图，斜坡的坡度为，坡长为26米，在坡顶A处的同一水平面上有一座古塔BC，在斜坡底P处测得该塔的塔顶B的仰角为45，在坡顶A处测得该塔的塔顶B的仰角为76求：（1）坡顶A到地面PQ的距离；
17、（2）古塔BC的高度（结果精确到1米）ABCPQDE（参考数据：，）【难度】【答案】（1）10；（2）19【解析】解：延长BC交PQ于点E，过A作ADPQ由题意可知：，在中，设，则，在中，设，在中，【总结】本题主要考查利用坡脚和坡比的概念以及锐角三角比的相关概念解决实际问题【例28】 如图，某堤坝的横截面是梯形ABCD，背水坡AD的坡度i为1 : 1.2，坝高为5米现为了提高堤坝的防洪能力，市防汛指挥部决定加固堤坝，要求坝顶CD加宽1米，形成新的背水坡EF，其坡度为1 : 1.4，已知堤坝总长度为4000米（1）求完成该工程需要多少立方米的土？ABCDEFGH（2）该工程由甲、乙两个工程队同时
18、合作完成按原计划需要20天准备开工前接到上级通知，汛期可能提前，要求两个工程队提高工作效率，甲队工作效率提高30%，乙队工作效率提高40%，结果提前5天完成问这两个工程队原计划每天各完成多少立方米？【难度】【答案】（1）30000；（2）甲：1000；乙：500【解析】由题意可知：，在中，在中，（2）设原计划甲工程队每天完成立方米，乙工程队每天完成立方米，则根据题意可得：，解得：原计划甲工程队每天完成1000立方米，乙工程队每天完成500立方米【总结】本题主要考查利用坡脚和坡比的概念以及锐角三角比的相关概念解决实际问题ABCDEFGH【例29】 如图所示，在风景区观测塔高时，塔的底部不能直接到
19、达测绘员从观景台（横截面为梯形）的底部沿坡面方向走30米到达顶部处，用测角仪（测角仪的高度忽略不计）在点处测得塔顶E的仰角是45，沿方向走20米到达点处测得塔顶E的仰角是60已知坡面的坡度是，根据上述测量数据能否求出塔高？若能，请求出塔高（精确到1米）；若不能，说明还需测出哪些量才能求出塔高【难度】【答案】能，62米【解析】由题意可知：，过B作BHAD在中，设，在中，【总结】本题主要考查利用坡脚和坡比的概念以及锐角三角比的相关概念解决实际问题，注意认真分析题目中的条件，分析清楚仰角分别指的是哪个角【例30】 如图，小智所住的楼房在一个不高的斜坡EF上，楼房旁边不远处有一棵笔直而垂直于水平地面B
20、E的大树HD小智想要测量这棵大树HD的高度在下午的某个时刻，他观察到这棵大树树梢H的影子落在楼房的外墙面上的点G处同时，他又观察到在大树旁边有一根笔直而垂直于水平地面BE的木柱AB，它在水平地面BE上的影子BC也清晰可见小智通过测量得到以下一些数据：AB = 1.6米，BC = 3.2米，DE = 7.2米，EF = 2.6米，斜坡EF的坡度i =1 : 2.4，FG = 1.6米试求大树HD的高ABCDEFGHMN【难度】【答案】7.4米【解析】解：由题意可得：，过F作FMHD，过F作FNDN在中，设，则，在中，【总结】本题主要考查利用坡脚和坡比的概念以及锐角三角比的相关概念解决实际问题，注
21、意认真分析题目中的条件随堂检测【习题1】 某飞机在离地面1200米的上空测得地面控制点的俯角为60，此时飞机与该地面控制点之间的距离是_米【难度】 【答案】【解析】考查俯角的定义【习题2】 一船在海上点B处沿南偏东10方向航行到点C处，这时在小岛A测得点C在南偏西80方向，则_【难度】【答案】90【解析】考查方向角的定义【习题3】 某人沿着有一定坡度的坡面前进了10米，此时他与水平地面的垂直距离为米，则这个坡面的坡度为_【难度】【答案】1:2【解析】考查坡度的定义ABCDE【习题4】 如图，已知楼房AB高50米，铁塔塔基距楼房房基间的水平距离BD = 50米，塔高DC为米，下列结论中，正确的是
22、（ ）A由楼顶望塔顶仰角为60B由楼顶望塔基俯角为60C由楼顶望塔顶仰角为30D由楼顶望塔基俯角为30【难度】【答案】C【解析】解：由图可知：， 在中， 由楼顶望塔顶仰角为30【总结】本题主要考查利用已知条件解直角三角形，再利用锐角三角比的值求出角的度数【习题5】 A港在B地的正南千米处，一艘轮船由A港开出向西航行，某人第一次在B处望见该船在南偏西30，半小时后，有望见该船在南偏西60，则该船速度为_【难度】【答案】40【解析】解：在中，解得：在中，解得：，【总结】本题主要考查利用方位角解决实际问题DABCNM【习题6】 如图，一架飞机在高度为5千米的点A时，测得前方的山顶D的俯角为30，水平
23、向前飞行2千米到达点B时，又测得山顶D的俯角为45，求这座山的高度DN（结果可保留根号）【难度】【答案】米【解析】解：由题意可得：，设，则在中，解得：，【总结】本题主要考查利用仰角和俯角的有关概念解决实际问题【习题7】 小岛B正好在深水港口A的东南方向，一艘集装箱货船从港口A出发，沿正东方向以每小时30千米的速度行驶，40分钟后在C处测得小岛B在它的南偏东15方向，求小岛B离深水港口A的距离(精确到0.1千米)ABC北北D（参考数据：，）【难度】【答案】38.6千米【解析】解：由题意可得：，过C点作CDAB在中，解得：，在中，解得：【总结】本题主要考查利用方位角解决实际问题【习题8】 如图，以
24、水库大坝横断面是梯形ABCD，坝顶宽6米，坝高23米，斜坡AB的坡度，斜坡CD的坡度（1）求斜坡AB和坝底AD的长度；ABCDEF（2）若要把坝宽增加3米，同时背水坡AB的坡度由原来的1 : 3变为1 : 5，请求出大坝横断面的面积增加了多少平方米【难度】【答案】（1），132.5；（2）598【解析】解：由题意可得：，在中，解得：在中，解得：（2）由（1）可得：在中，【总结】本题主要考查利用坡度来解决实际问题，注意对题目中条件的认真分析ABCDEFGH【习题9】 某城市规划期间，欲拆除河岸边的一根电线杆AB（如图），已知距电线杆AB水平距离14米处是河岸，即BD = 14米，该河岸的坡面CD
25、的坡比为1 : 2，岸高CF为2米，在坡顶C处测得杆顶A的仰角为30，D、E之间是宽2米的人行道，请你通过计算说明在拆除电线杆AB时，为确保安全，是否需要将此人行道封上？（在地面上以点B为圆心，以AB长为半径的圆形区域为危险区域）【难度】【答案】不需要将此人行道封上【解析】解：由题意可知：，在中，解得：，在中，解得：，不需要将此人行道封上【总结】本题主要考查利用坡度来解决实际问题，注意对题目中条件的认真分析【习题10】 如图，小唐同学在操场上放风筝，风筝从A处起飞，一会儿便飞抵C处，此时，在AQ延长线B处的小宋同学，发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上（1）已知旗杆高为10米，若
26、在B处测得旗杆顶点P的仰角为30，A处测得点P的仰角为45，试求A、B之间的距离；ABCDPQE（2）此时，在A处背向旗杆又测得风筝的仰角为75若绳子在空中视为一条线段，求绳子AC约为多长？（结果保留根号）【难度】【答案】【解析】解：（1）由题意可知：，在中，解得：，（2） 由题意有：过A作AEBC，在中，解得：，在中，解得：【总结】本题综合性较强，主要是利用已知条件，结合仰角和俯角的运用解直角三角形课后作业【作业1】 身高相同的三个小朋友甲、乙、丙放风筝，他们放出的线长分别为300米，250米，200米，线与地面所成的角度分别为30，45，60（假设风筝线是拉直的），则三人所放的风筝（ ）A
27、甲的最高B乙的最低C丙的最低D乙的最高【难度】 【答案】D【解析】由仰角的定义和解直角三角形可得：甲的风筝离地面150米，乙的风筝离地面米，丙的风筝离地面米乙的风筝最高【总结】本题主要考查方位角的概念以及特殊角的锐角三角比的值【作业2】 小明在东西方向是沿江大道A处，测得江中灯塔P在北偏东60方向上，在A处正东400米的B处，测得江中灯塔P在北偏东30方向上，则灯塔P到沿江大道的距离为_米【难度】【答案】【解析】解：由题意可知：，过P作PCAB，垂足为C在中，【总结】本题主要考查方位角的概念及运用【作业3】 某人从地面沿着坡度的山坡走了100米，这时他离地面的高度是_米【难度】【答案】50【解
28、析】考查坡度的定义和解直角三角形【作业4】 如图，一渔船上的渔民在A处看见灯塔M在北偏东60的方向，这艘渔船以28海里/时的速度向正东航行，半小时到达B处，在B处看见灯塔M在北偏东15的方向，此时灯塔M与渔船的距离是（ ）ABM北东CA14海里B海里C7海里D海里【难度】【答案】D【解析】解：由题意有：，过B作BCAM，垂足为C在中，；在中，【总结】本题主要考查利用方位角结合锐角三角比解决实际问题ABCDEF【作业5】 如图，在同一地面上有甲、乙两幢楼AB、CD，甲楼AB高10米，从甲楼AB的楼顶测得乙楼CD的楼顶C的仰角为30，从乙楼CD的楼顶C拉下的节日庆典条幅CE与地面所成的角为60，这
29、时条幅与地面的固定点E到甲楼B的距离为24米，求条幅CE的长度【难度】【答案】米【解析】解：由题意可知：，设，则，在中，【总结】本题主要考查利用仰角和俯角的相关概念结合锐角三角比解决实际问题【作业6】 如图，水坝的横截面是梯形，上底= 4米，坝高米，斜坡的坡比，斜坡的坡比（1）求坝底的长；（结果保留根号）（2）为了增加水坝的抗洪能力，在原来的水坝上增加高度，使得水坝的上底米，求水坝增加的高度（精确到0.1米，参考数据）ABCDNMABCDNMEFGH【难度】【答案】（1）；（2）0.7米【解析】解：（1）在中，在中，(2)在中，在中，设，则，【总结】本题主要考查利用坡度和坡比的相关概念结合锐角
30、三角比解决实际问题ABCDC1【作业7】 如图，某人在建筑物AB的顶部测得一烟囱CD的顶端C的仰角为45，测得点C在湖中的倒影C1的俯角为60，已知AB = 20米，求烟囱CD的高【难度】E【答案】米【解析】解：由题意可得：，过A作AECD，垂足为E设，则C和C1关于BD对称，在中，【总结】本题主要考查利用俯角的相关概念结合锐角三角比解决实际问题，注意认真分析ABCDEFGHMN【作业8】 如图，一水渠的横断面是等腰梯形，已知其迎水斜坡AD和BC的坡度为1：0.6，现在测得放水前的水面宽EF为1.2米，当水闸放水后，水渠内水面宽GH为2.1米，求放水后水面上升的高度【难度】【答案】放水后水面上
31、升的高度为0.75米【解析】解：由题意可知：四边形GEFH为等腰梯形过E作EMGH，过F作FNGH由等腰梯形的性质可得：在中，放水后水面上升的高度为0.75米【总结】本题主要考查利用坡度和坡比的相关概念结合锐角三角比解决实际问题【作业9】 台风是一种自然灾害，它以台风中心为圆心，在周围数十千米范围内形成气旋风暴，有极强的破坏力据气象观测，距沿海某城市的正南方向220千米的处有一台风中心，其中心最大风力为12级，每远离台风中心20千米，风力就减弱一级，该台风中心现在以每小时15千米的速度沿北偏东方向往移动，且台风中心风力不变，若城市所受风力达到四级，则称受台风影响（1）该城市是否会受这次台风影响
32、？请说明理由（2）若受台风影响，那么台风影响该城市的持续时间会有多长？ABC（3）该城市受台风影响的最大风力是几级？【难度】D【答案】（1）受影响；（2） ；（3） 6.5级【解析】解：（1）会受到台风影响 过A作ADBC台风在移动时，距离A最近D处时，在中，11020=5.5；12-5.5=6.5；6.5超过4级，受台风影响（2）当台风在移动，其与A距离是时开始受影响或结束影响持续时间为（3）由（1）可得：该城市受台风影响的最大风力是6.5级【总结】本题主要考查对方位角的理解以及是否受影响的理解，解题时要认真分析题意【作业10】 如图，小明发现在小丘上种植着一棵香樟树AB，它的影子恰好落在丘顶平地BC和斜坡的坡面CD上小明测得BC = 4米，斜坡的坡面CD的坡度为，CD =2.5米如果小明同时还测得附近的一根垂直于地面的2米高的木柱MN的影长NP = 1.5米，求这棵香樟树AB的高度ABCD光线PNMEF【难度】【答案】6.5米【解析】解：由题意可得：，设，在中，【总结】本题综合性较强，考查的知识点比较多，要认真分析题意，并且熟练使用相似的性质以及通过锐角三角比解直角三角形的方法
