1、第 1 页 共 9 页2017年九年级数学中考模拟试卷一 、填空题：1.若|2x1|=3，则 x= 2.如图,已知AFEC,ABCD,A=65,则C= 度3.分解因式：x 2+2x-3=_.4.正多边形的一个外角等于 20，则这个正多边形的边数是_5.设 x1，x 2是一元二次方程 x22x3=0 的两根，则 x12+x22= 6.如图所示，正方形 ABCD对角线 AC所在直线上有一点 O，OA=AC=2，将正方形绕 O点顺时针旋转 60，在旋转过程中，正方形扫过的面积是 二 、选择题：7.据统计 2014年我国高新技术产品出口总额 40570亿元，将数据 40570亿用科学记数法表示为（ ）
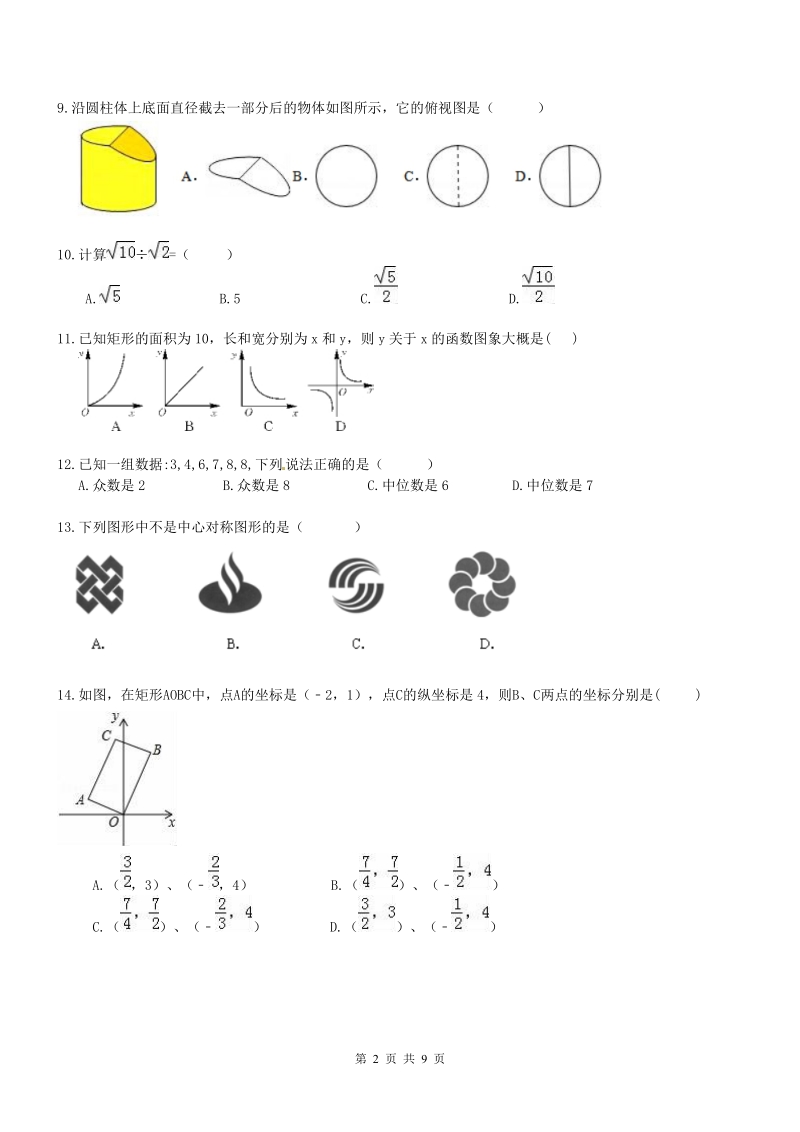
2、A.4.0570109 B.0.405701010 C.40.5701011 D.4.057010128.小华同学接到通知，她的作文通过了我的中国梦征文选拔，需尽快上交该作文的电子文稿，接到通知后，小华立即在电脑上打字录入这篇文稿，录入一段时间后因事暂停，过了一小会儿，小华继续录入并加快了录入速度，直至录入完成，设从录入文稿开始所经过的时间为x，录入字数为y，下面能反映y与x之间的关系的大致图象是（ ）A. B. C. D.第 2 页 共 9 页9.沿圆柱体上底面直径截去一部分后的物体如图所示，它的俯视图是（ ）10.计算 =（ ）A. B.5 C. D.11.已知矩形的面积为 10，长和宽分
3、别为 x和 y，则 y关于 x的函数图象大概是( ) 12.已知一组数据:3,4,6,7,8,8,下列 说法正确的是（ ）A.众数是 2 B.众数是 8 C.中位数是 6 D.中位数是 713.下列图形中不是中心对称图形的是（ ）14.如图，在矩形AOBC中，点A的坐标是（2，1），点C的纵坐标是 4，则B、C两点的坐标分别是( )A.（ ，3）、（ ，4） B.（ ）、（ ） C.（ ）、（ ） D.（ ）、（ ）第 3 页 共 9 页三 、解答题：15.解不等式组： ，并把解集在数轴上表示出来16.如图，ABC 和ADE 都是等腰三角形，且BAC=90，DAE=90，B，C，D 在同一条直
4、线上求证：BD=CE17.倡导健康生活,推进全民健身,某社区要购进 A,B两种型号的健身器材若干套,A,B 两种型号健身器材的购买单价分别为每套 310元,460 元,且每种型号健身器材必须整套购买（1）若购买 A,B两种型号的健身器材共 50套,且恰好支出 20000元,求 A,B两种型号健身器材各购买多少套？（2）若购买 A,B两种型号的健身器材共 50套,且支出不超过 18000元,求 A种型号健身器材至少要购买多少套？第 4 页 共 9 页18.如图，四边形ABCD中，对角线AC、BD相交于点O，AO=CO，BO=DO，且ABC+ADC=180（1）求证：四边形ABCD是矩形（2）若A
5、DF：FDC=3：2，DFAC，则BDF的度数是多少？19.某校为了了解本校九年级女生体育项目跳绳的训练情况，让体育老师随机抽查了该年级若干名女生，并严格地对她们进行了 1分钟跳绳测试，同时统计每个人跳的个数（假设这个个数为 x），现在我们将这些同学的测试结果分为四个等级：优秀（ x180），良好（150 x179），及格（135 x149）和不及格（ x134），并将统计结果绘制成如下两幅不完整的统计图。根据以上信息，回答下列问题：（1）本次共测试了 名女生，其中等级为“良好”的有 人；（2）请计算等级为“及格”所在圆心角的度数；（3）若该年级有 300名女生，请你估计该年级女生中 1分钟“
6、跳绳”个数达到优秀的人数。第 5 页 共 9 页20.如图，AB为O的直径，C为O上一点，AD和过C点的直线互相垂直，垂足为D，且AC平分DAB（1）求证：DC为O的切线；（2）若O的半径为 5，BC=6，求CD的长21.可以在箱子里先后摸出两个球（第一次摸出后不放回）商场根据两小球所标金额的和返还相等价格的购物券，购物券可以在本商场消费某顾客刚好消费 300元（1）该顾客至多可得到 元购物券；（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于 50元的概率22.如图，排球运动员站在点 O处练习发球，将球从点 O正上方 2米的点 A处发出把球看成点，其运行的高度y（米）与运行
7、的水平距离 x（米）满足关系式 y=a（x6） 2，已知 球网与点 O的水平距离为 9米，高度为2.43米，球场的边界距点 O的水平距离为 18米（1）当 h=2.6时，求 y与 x的函数关系式（2）当 h=2.6时，球能否越过球网？球会不会出界？请说明理由（3）若球一定能越过球网，又不出边界则 h的取值范围是多少？第 6 页 共 9 页23.如图甲，ABBD，CDBD，APPC，垂足分别为 B、P、D，且三个垂足在同一直线上，我们把这样的图形叫“三垂图”（1）证明：ABCD=PBPD（2）如图乙，也是一个“三垂图”，上述结论成立吗？请说明理由（3）已知抛物线与 x轴交于点 A（1，0），B（
8、3，0），与 y轴交于点（0，3），顶点为 P，如图丙所示，若 Q是抛物线上异于 A、B、P 的点，使得QAP=90，求 Q点坐标第 7 页 共 9 页参考答案1.答案为：2 或12.答案为：653.答案为：(x+3)(x-1)；4.答案为：185.答案为：106.答案为：2+27.D8.C9.D10.A11.C12.B13.B14.D15.答案为：1x3.16.【解答】证明：ABC 和ADE 都是等腰直角三角形AD=AE，AB=AC，又EAC=90+CAD，DAB=90+CAD，DAB=EAC，在ADB 和AEC 中 ADBAEC（SAS），BD=CE17.【解答】解：（1）设购买 A种型号
9、健身器材 x套，B 型器材健身器材 y套，根据题意，得： ，解得： ，答：购买 A种型号健身器材 20套，B 型器材健身器材 30套（3）设购买 A型号健身器材 m套，根据题意，得：310m+460（50m）18000，解得：m33 ，m 为整数，m 的最小值为 34，答：A 种型号健身器材至少要购买 34套18.（1）证明：AO=CO，BO=DO四边形ABCD是平行四边形，ABC=ADC，ABC+ADC=180，ABC=ADC=90，四边形ABCD是矩形；（2）解：ADC=90，ADF：FDC=3：2，FDC=36，DFAC，DCO=9036=54，四边形ABCD是矩形，OC=OD，ODC=
10、54BDF=ODCFDC=1819.20.解：（1）证明：连接OC如图 1所示AC平分DAB，DAC=OAC，第 8 页 共 9 页OA=OC，OCA=OAC，DAC=OCA，DAOC，ADDC，ADC=90，OCD=90，即OCDC，OC为半径，DC为O的切线（2）解：连接BC，如图 2所示：AB是O的直径，AB=10，ACB=90=ADC，AC=8，又DAC=OAC，ACDABC， ，即 ，解得：CD=4.821.【解答】解：（1）则该顾客至多可得到购物券：50+20=70（元）；故答案为：70；（2）画树状图得：共有 12种等可能的结果，该顾客所获得购物券的金额不低于 50元的有 6种情况，该顾客所获得购物券的金额不低于 50元的概率为：0.522.23.【解答】（1）证明：ABBD，CDBD，B=D=90，A+APB=90，第 9 页 共 9 页APPC，APB+CPD=90，A=CPD，ABPPCD，AB:PD=PB:CD，ABCD=PBPD；（2）ABCD=PBPD 仍然成立理由如下：ABBD，CDBD，B=CDP=90，A+APB=90，APPC，APB+CPD=90，A=CPD，ABPPCD，AB:PD=PB:CD，ABCD=PBPD；
