1、第 1 页（共 35 页）2016 年北京市顺义区中考数学一模试卷一、选择题（本题共 30 分，每小题 3 分）下面各题均有四个选项，其中只有一个是符合题意的1中国传统节日清明节距今已有二千五百多年的历史，是最重要的祭祀节日之一，是祭祖和扫墓的日子2016 年 4 月 4 日是今年的清明节，全国各地迎来群众集中祭扫高峰根据民政部清明节工作办公室对全国 150 个祭扫观察点数据统计分析，当日共接待祭扫群众 5 433 000 人次，把 5 433 000 用科学记数法表示正确的是（ ）A5.433 107 B5.43310 6 C543.3 104 D543310 32实数 a，b 在数轴上的对
2、应点的位置如图所示，化简|ab|的结果是（ ）A0 Ba+b Ca b Db a3一个三棱柱如图所示，它的主视图是（ ）A B C D4九（2）班“环保小组”的 5 位同学在一次活动中捡废弃塑料袋的个数分别为：4，6 ，8 ，16 ，16 这组数据的中位数、众数分别为（ ）A16， 16 B10，16 C8，8 D8，165下列交通标志中，是轴对称图形的是（ ）A B C D6如图，为测量池塘岸边 A、B 两点之间的距离，小亮在池塘的一侧选取一点O，测得 OA、OB 的中点 D、E 之间的距离是 14 米，则 A、B 两点之间的距离是第 2 页（共 35 页）（ ）A18 米 B24 米 C2
3、8 米 D30 米7小林给弟弟买了一些糖果，放到一个不透明的袋子里，这些糖果除了口味和外包装的颜色外其余都相同，袋子里各种口味糖果的数量统计如图所示，他让弟弟从袋子里随机摸出一颗糖果则弟弟恰好摸到橘子味糖果的概率是（ ）A B C D8若关于 x 的一元二次方程 x22x+m3=0 有两个不相等的实数根，则 m 的取值范围是（ ）Am 2 Bm4 Cm4 Dm49某公司有如表几种手机 4G 套餐：（1G=1024M）套餐内包含内容 套餐外资费套餐类型 月费（元/月）国内数据流量国内电话（分钟）流量 国内电话套餐 1 76 400M 200套餐 2 106 800M 300套餐 3 136 1G
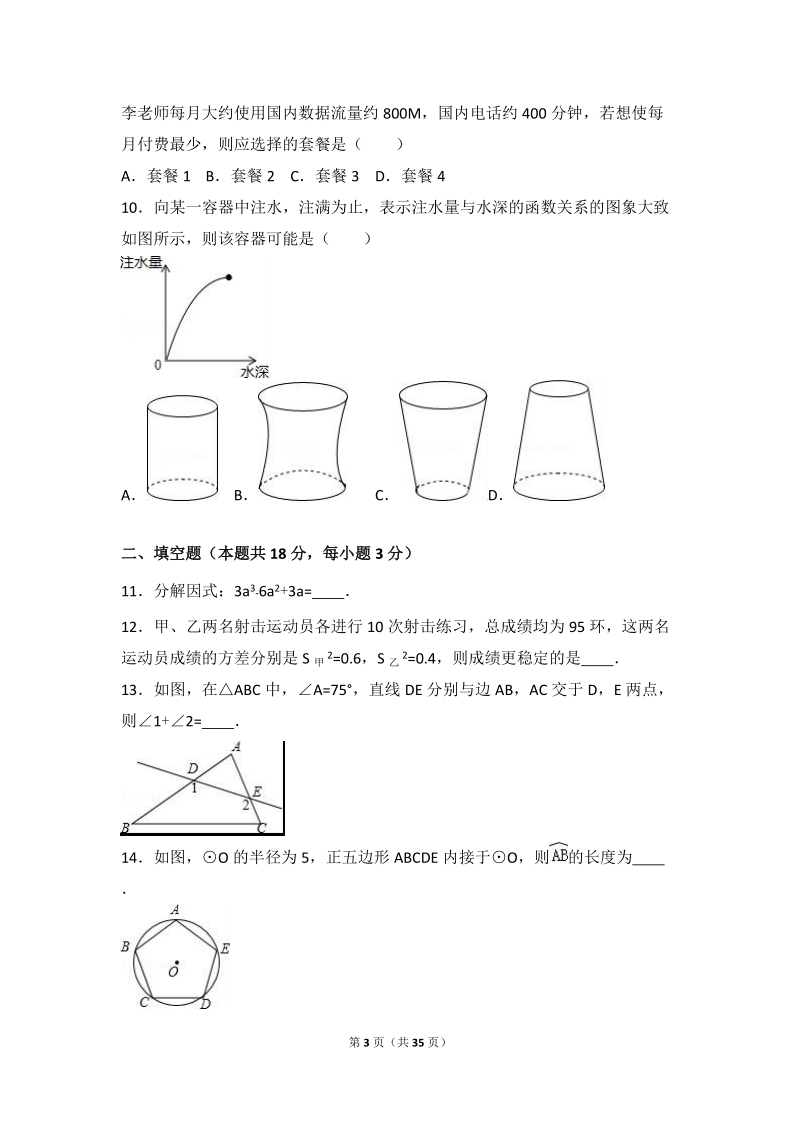
4、 500套餐 4 166 2G 5000M200M 时，0.3 元/M201M1G 时，60元0.15 元/分钟第 3 页（共 35 页）李老师每月大约使用国内数据流量约 800M，国内电话约 400 分钟，若想使每月付费最少，则应选择的套餐是（ ）A套餐 1 B套餐 2 C套餐 3 D套餐 410向某一容器中注水，注满为止，表示注水量与水深的函数关系的图象大致如图所示，则该容器可能是（ ）A B C D二、填空题（本题共 18 分，每小题 3 分）11分解因式：3a 36a2+3a= 12甲、乙两名射击运动员各进行 10 次射击练习，总成绩均为 95 环，这两名运动员成绩的方差分别是 S 甲
5、 2=0.6，S 乙 2=0.4，则成绩更稳定的是 13如图，在ABC 中， A=75，直线 DE 分别与边 AB，AC 交于 D，E 两点，则1+2= 14如图，O 的半径为 5，正五边形 ABCDE 内接于O，则 的长度为 第 4 页（共 35 页）15 算法统宗是中国古代数学名著，作者是我国明代数学家程大位在算法统宗中有一道“ 荡秋千” 的问题：“平地秋千未起，踏板一尺离地送行二步与人齐，五尺人高曾记仕女佳人争蹴，终朝笑语欢嬉良工高士素好奇，算出索长有几？”译文：“有一架秋千，当它静止时，踏板离地 1 尺，将它往前推送 10 尺（水平距离）时，秋千的踏板就和人一样高，这个人的身高为 5
6、尺，秋千的绳索始终拉得很直，试问绳索有多长？”设秋千的绳索长为 x 尺，根据题意可列方程为 16数学课上，同学们兴致勃勃地尝试着利用不同画图工具画一个角的平分线小明用直尺画角平分线的方法如下：（1）用直尺的一边贴在AOB 的 OA 边上，沿着直尺的另一条边画直线 m；（2）再用直尺的一边贴在AOB 的 OB 边上，沿着直尺的另一条边画直线 n，直线 m 与直线 n 交于点 D；（3）作射线 OD射线 OD 是AOB 的平分线请回答：小明的画图依据是 三、解答题（本题共 72 分，第 17-26 题，每小题 5 分，第 27 题 7 分，第 28题 7 分，第 29 题 8 分）解答应写出文字说
7、明，演算步骤或证明过程17计算：（ ） 2（3） 0 4cos30第 5 页（共 35 页）18已知 2x2+3x12=0，求代数式 x（32x）+（2x+3） （2x 3）的值19解不等式： ，并写出它的所有正整数解20已知：如图，B，A，E 在同一直线上，AC BD 且 AC=BE，ABC= D求证：AB=BD21进入春季，大家都喜欢周末户外踏青郊游，住在顺义同一小区的大明和小丽都和全家自驾车到金海湖旅游，下图是网上提供的驾车路线方案：实际出行时，大明选择了方案 1，小丽选择了方案 2，小丽平均每小时比大明多行 35 公里，结果大明所用时间是小丽的 1.5 倍，求两人去金海湖各用了多长时间
8、？22如图，在平面直角坐标系 xOy 中，直线 y=x+b 与双曲线 y= 相交于 A，B 两点，已知 A（2，5） （1）求 k 和 b 的值；（2）求OAB 的面积第 6 页（共 35 页）23如图，已知 E、F 分别是ABCD 的边 BC、AD 上的点，且 BE=DF（1）求证：四边形 AECF 是平行四边形；（2）若 BC=10，BAC=90，且四边形 AECF 是菱形，求 BE 的长24学习了数据的收集、整理与表示之后，某小组同学对本校“自主选修活动课”比较感兴趣，他们以问卷的形式随机调查了 40 名学生的选课情况（每人只能选一项） ，并统计如下：科目 篮球 围棋 剪纸 舞台剧 茶艺
9、 交谊舞 其它课计数 正正 正 正一 正一（1）请选择一种统计图将上表中的结果表示出来；（2）该校共有 500 名学生，请估计选修篮球课的人数；并说明你估计的理由；（3）谈谈你对该校“自主选修活动课”的科目设置有哪些建议？25如图，D 为O 上一点，点 C 在直径 BA 的延长线上，且CDA= CBD（1）求证：CD 是O 的切线；（2）过点 B 作O 的切线交 CD 的延长线于点 E，若 BC=6，tanCDA= ，求BE 的长26我们把过三角形的一个顶点且能将这个三角形分割成两个等腰三角形的线第 7 页（共 35 页）段称为该三角形的“ 等腰线段” 例如：RtABC，取边 AB 的中点 D
10、，线段 CD 就是ABC 的等腰线段（1）请分别画出下列三角形的等腰线段；（2）如图，在EFG 中，若G=2 F，且EFG 有等腰线段，请直接写出F的度数的取值范围27在平面直角坐标系 xOy 中，抛物线 y=ax22x 的对称轴为 x=1（1）求 a 的值及抛物线 y=ax22x 与 x 轴的交点坐标；（2）若抛物线 y=ax22x+m 与 x 轴有交点，且交点都在点 A（ 4，0） ，B（1 ，0）之间，求 m 的取值范围第 8 页（共 35 页）28已知：在ABC 中， BAC=60 （1）如图 1，若 AB=AC，点 P 在ABC 内，且APC=150，PA=3，PC=4，把APC 绕
11、着点 A 顺时针旋转，使点 C 旋转到点 B，得到ADB，连结 DP依题意补全图 1；直接写出 PB 的长；（2）如图 2，若 AB=AC，点 P 在ABC 外，且 PA=3，PB=5，PC=4，求APC 的度数；（3）如图 3，若 AB=2AC，点 P 在ABC 内，且 PA= ，PB=5，APC=120 ，直接写出 PC 的长29在平面直角坐标系 xOy 中，点 P（a，b ）的“变换点”Q 的坐标定义如下：当a b 时，Q 点坐标为（b ，a） ；当 ab 时，Q 点坐标为（ a，b） （1）求（2，3） ， （6，1）的变换点坐标；（2）已知直线 l 与 x 轴交于点 A（4，0） ，
12、与 y 轴交于点 B（0，2） 若直线 l 上所有点的变换点组成一个新的图形，记作图形 W，请画出图形 W，并简要说明画图的思路；（3）若抛物线 y= x2+c 与图形 W 有三个交点，请直接写出 c 的取值范围第 9 页（共 35 页）2016 年北京市顺义区中考数学一模试卷参考答案与试题解析一、选择题（本题共 30 分，每小题 3 分）下面各题均有四个选项，其中只有一个是符合题意的1中国传统节日清明节距今已有二千五百多年的历史，是最重要的祭祀节日之一，是祭祖和扫墓的日子2016 年 4 月 4 日是今年的清明节，全国各地迎来群众集中祭扫高峰根据民政部清明节工作办公室对全国 150 个祭扫观
13、察点数据统计分析，当日共接待祭扫群众 5 433 000 人次，把 5 433 000 用科学记数法表示正确的是（ ）A5.433 107 B5.43310 6 C543.3 104 D543310 3【考点】科学记数法表示较大的数【分析】科学记数法的表示形式为 a10n 的形式，其中 1|a |10，n 为整数确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位， n 的绝对值与小数点移动的位数相同当原数绝对值1 时，n 是正数；当原数的绝对值1 时，n 是负数【解答】解：将 5 433 000 用科学记数法表示为 5.433106故选 B2实数 a，b 在数轴上的对应点的位置如图所
14、示，化简|ab|的结果是（ ）A0 Ba+b Ca b Db a【考点】实数与数轴【分析】根据数轴可得 b0a，再根据负数的绝对值是它的相反数即可解答【解答】解：由数轴可得 b0a，a b0 ，第 10 页（共 35 页）|a b|=ab，故选：C3一个三棱柱如图所示，它的主视图是（ ）A B C D【考点】简单几何体的三视图【分析】直接利用几何体的形状进而得出其主视图【解答】解：如图所示：这个三棱柱，它的主视图是 故选：B4九（2）班“环保小组”的 5 位同学在一次活动中捡废弃塑料袋的个数分别为：4，6 ，8 ，16 ，16 这组数据的中位数、众数分别为（ ）A16， 16 B10，16 C
15、8，8 D8，16【考点】众数；中位数【分析】根据众数和中位数的定义求解找出次数最多的数为众数；把 5 个数按大小排列，位于中间位置的为中位数【解答】解：在这一组数据中 16 是出现次数最多的，故众数是 16；而将这组数据从小到大的顺序排列后，处于中间位置的数是 8，那么由中位数的定义可知，这组数据的中位数是 8故选 D5下列交通标志中，是轴对称图形的是（ ）第 11 页（共 35 页）A B C D【考点】轴对称图形【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可【解答】解：A、是轴对称图形，故此选项
16、正确；B、不是轴对称图形，故此选项错误；C、不是轴对称图形，故此选项错误；D、不是轴对称图形，故此选项错误；故选：B6如图，为测量池塘岸边 A、B 两点之间的距离，小亮在池塘的一侧选取一点O，测得 OA、OB 的中点 D、E 之间的距离是 14 米，则 A、B 两点之间的距离是（ ）A18 米 B24 米 C28 米 D30 米【考点】三角形中位线定理【分析】根据三角形中位线定理可知 DE= AB，由此即可解决问题【解答】解：OD=DA，OE=EB，DE= AB，DE=14m，AB=28m，故选 C第 12 页（共 35 页）7小林给弟弟买了一些糖果，放到一个不透明的袋子里，这些糖果除了口味和
17、外包装的颜色外其余都相同，袋子里各种口味糖果的数量统计如图所示，他让弟弟从袋子里随机摸出一颗糖果则弟弟恰好摸到橘子味糖果的概率是（ ）A B C D【考点】概率公式；条形统计图【分析】先利用条形统计图得到葡萄味糖果有 3 颗，草莓味糖果有 3 颗，椰子味糖果有 5 颗，苹果味糖果有 3 颗，然后根据概率公式求解【解答】解：根据统计图得葡萄味糖果有 3 颗，草莓味糖果有 3 颗，橘子味糖果有 5 颗，苹果味糖果有 3 颗，所以小明抽到橘子味糖果的概率= = 故选 B8若关于 x 的一元二次方程 x22x+m3=0 有两个不相等的实数根，则 m 的取值范围是（ ）Am 2 Bm4 Cm4 Dm4【
18、考点】根的判别式【分析】根据一元二次方程的根的判别式，建立关于 m 的不等式，求出 m 的取第 13 页（共 35 页）值范围即可【解答】解：关于 x 的一元二次方程 x22x+m3=0 有两个不相等的实数根，=b 24ac=441（m 3）0，m4m 的取值范围是 m4；故选 D9某公司有如表几种手机 4G 套餐：（1G=1024M）套餐内包含内容 套餐外资费套餐类型 月费（元/月）国内数据流量国内电话（分钟）流量 国内电话套餐 1 76 400M 200套餐 2 106 800M 300套餐 3 136 1G 500套餐 4 166 2G 5000M200M 时，0.3 元/M201M1G
19、 时，60元0.15 元/分钟李老师每月大约使用国内数据流量约 800M，国内电话约 400 分钟，若想使每月付费最少，则应选择的套餐是（ ）A套餐 1 B套餐 2 C套餐 3 D套餐 4【考点】有理数的混合运算【分析】根据每种套餐的优惠方法分别求出每种套餐的费用，再找出最划算的套餐即可【解答】解：套餐 1：76+2000.3+60+0.15=76+60+60+0.15200=76+60+60+30=226（元） ；套餐 2：106 +0.15第 14 页（共 35 页）=106+0.15100=106+15=121（元） ；套餐 3：136 元；套餐 4：166 元121 136 16622
20、6，应选择的套餐是套餐 2故选：B10向某一容器中注水，注满为止，表示注水量与水深的函数关系的图象大致如图所示，则该容器可能是（ ）A B C D【考点】函数的图象【分析】根据函数的图象和所给出的图形分别对每一项进行判断即可【解答】解：当容器是圆柱时，容积 V=r2h，r 不变，V 是 h 的正比例函数，其图象是过原点的直线，则 A 不满足条件；由函数图象看出，随着高度的增加注水量也增加，但随水深变大，每单位高度的增加，体积的增加量变小，图象上升趋势变缓，则容器平行底的截面的半径由下到上逐渐变小则 B、C 不满足条件；而 D 满足条件；故选：D第 15 页（共 35 页）二、填空题（本题共 1
21、8 分，每小题 3 分）11分解因式：3a 36a2+3a= 3a（a 1） 2 【考点】提公因式法与公式法的综合运用【分析】先提取公因式 3a，再根据完全平方公式进行二次分解完全平方公式：a22ab+b2=（ab） 2【解答】解：3a 36a2+3a=3a（a 22a+1）=3a（a1） 2故答案为：3a（a1 ） 212甲、乙两名射击运动员各进行 10 次射击练习，总成绩均为 95 环，这两名运动员成绩的方差分别是 S 甲 2=0.6，S 乙 2=0.4，则成绩更稳定的是 乙 【考点】方差【分析】由方差反映了一组数据的波动情况，方差越小，则数据的波动越小，成绩越稳定可以作出判断【解答】解：
22、S 甲 2=0.6，S 乙 2=0.4，则 S 甲 2S 乙 2，可见较稳定的是乙故答案为：乙13如图，在ABC 中， A=75，直线 DE 分别与边 AB，AC 交于 D，E 两点，则1+2= 255 【考点】三角形内角和定理【分析】根据三角形的内角和定理结合A 的度数，即可得出ADE+AED 的度数，再由ADE 与1 互补、AED 与2 互补，代入数据即可得出结论【解答】解：A=75，ADE+AED=180 A=105，第 16 页（共 35 页）又1=180ADE，2=180AED，1+2=360（ADE+AED）=255故答案为：25514如图，O 的半径为 5，正五边形 ABCDE
23、内接于O，则 的长度为 2 【考点】正多边形和圆；弧长的计算【分析】利用正五边形的性质得出中心角度数，进而利用弧长公式求出即可【解答】解：如图所示：O 为正五边形 ABCDE 的外接圆，O 的半径为 5，AOB= =72， 的长为： =2故答案为 215 算法统宗是中国古代数学名著，作者是我国明代数学家程大位在算法统宗中有一道“ 荡秋千” 的问题：“平地秋千未起，踏板一尺离地送行二步与人齐，五尺人高曾记仕女佳人争蹴，终朝笑语欢嬉良工高士素好奇，算出索长有几？”译文：“有一架秋千，当它静止时，踏板离地 1 尺，将它往前推送 10 尺（水平距离）时，秋千的踏板就和人一样高，这个人的身高为 5 尺，
24、秋千的绳索始终拉得很直，试问绳索有多长？”设秋千的绳索长为 x 尺，根据题意可列方程为 x 2=102+（x 4） 2 第 17 页（共 35 页）【考点】勾股定理的应用【分析】设秋千的绳索长为 x 尺，根据题意可得 AB=（x4）尺，利用勾股定理可得 x2=102+（x4） 2【解答】解：设秋千的绳索长为 x 尺，根据题意可列方程为：x2=102+（x4） 2，故答案为：x 2=102+（x4） 216数学课上，同学们兴致勃勃地尝试着利用不同画图工具画一个角的平分线小明用直尺画角平分线的方法如下：（1）用直尺的一边贴在AOB 的 OA 边上，沿着直尺的另一条边画直线 m；（2）再用直尺的一边
25、贴在AOB 的 OB 边上，沿着直尺的另一条边画直线 n，直线 m 与直线 n 交于点 D；（3）作射线 OD射线 OD 是AOB 的平分线请回答：小明的画图依据是 到角的两边距离相等的点在这个角的角平分线上 第 18 页（共 35 页）【考点】作图基本作图【分析】利用画法可点 D 到 OA 和 OC 的距离相等（尺的宽度相等） ，然后根据角平分线的性质定理判断四边形 EEOC 为菱形，然后根据菱形的性质可判定 OD 为AOB 的平分线【解答】解：由画法可知，点 D 到 OA 和 OC 的距离相等，所以 OD 平分AOB故答案为到角的两边距离相等的点在这个角的角平分线上三、解答题（本题共 72
26、 分，第 17-26 题，每小题 5 分，第 27 题 7 分，第 28题 7 分，第 29 题 8 分）解答应写出文字说明，演算步骤或证明过程17计算：（ ） 2（3） 0 4cos30【考点】实数的运算；零指数幂；负整数指数幂；特殊角的三角函数值【分析】原式利用零指数幂、负整数指数幂法则，二次根式性质，以及特殊角的三角函数值计算即可得到结果【解答】解：原式=41+2 4 =3第 19 页（共 35 页）18已知 2x2+3x12=0，求代数式 x（32x）+（2x+3） （2x 3）的值【考点】整式的混合运算化简求值【分析】原式利用单项式乘以多项式，平方差公式化简，去括号合并得到最简结果，
27、把已知等式变形后代入计算即可求出值【解答】解：2x 2+3x12=0，2x 2+3x=12，则原式=3x2x 2+4x29=2x2+3x9=129=319解不等式： ，并写出它的所有正整数解【考点】一元一次不等式的整数解；解一元一次不等式【分析】去分母，去括号，移项，合并同类项，系数化成 1 即可求得不等式的解集，然后确定正整数解即可【解答】解：去分母，得 3（x+3 ） 2（2x 1）6，去括号，得 3x+94x+26，移项，得 3x4x692，合并同类项，得x5，系数化成 1 得 x5则正整数解是 1，2，3，420已知：如图，B，A，E 在同一直线上，AC BD 且 AC=BE，ABC=
28、 D求证：AB=BD【考点】全等三角形的判定与性质第 20 页（共 35 页）【分析】根据平行线的性质和全等三角形的判定和性质证明即可【解答】证明：ACBD，BAC=DBE，在ABC 与BDE 中，ABCBDE （AAS） ，AB=BD21进入春季，大家都喜欢周末户外踏青郊游，住在顺义同一小区的大明和小丽都和全家自驾车到金海湖旅游，下图是网上提供的驾车路线方案：实际出行时，大明选择了方案 1，小丽选择了方案 2，小丽平均每小时比大明多行 35 公里，结果大明所用时间是小丽的 1.5 倍，求两人去金海湖各用了多长时间？【考点】分式方程的应用【分析】设小丽用 x 小时，则大明用 1.5x 小时，根
29、据“大明所用时间是小丽的1.5 倍”列出方程，解方程即可【解答】解：设小丽用 x 小时，则大明用 1.5x 小时，根据题意得： ，解得：x=1，经检验：x=1 是原方程的解，且符合题意，第 21 页（共 35 页）1.5x=1.5，答：小丽用 1 小时，则大明用 1.5 小时22如图，在平面直角坐标系 xOy 中，直线 y=x+b 与双曲线 y= 相交于 A，B 两点，已知 A（2，5） （1）求 k 和 b 的值；（2）求OAB 的面积【考点】反比例函数与一次函数的交点问题【分析】 （1）由直线 y=x+b 与双曲线 y= 相交于 A，B 两点，A（2，5） ，即可得到结论；（2）过 A 作
30、 ADx 轴于 D，BEx 轴于 E 根据 y=x+3，y= ，得到 B（5， 2） ，C（ 3，0） ，求出 OC=3，然后根据三角形的面积公式即可得到结论【解答】解：（1）直线 y=x+b 与双曲线 y= 相交于 A，B 两点，已知A（2 ，5 ） ，5=2+b，5= ，解得：k=10，b=3；（2）过 A 作 ADx 轴于 D，BEx 轴于 E，k=10，b=3，y=x+3，y= ，B（5， 2） ，C （3，0） ，第 22 页（共 35 页）OC=3，S AOC = OCAD= 35= ，S BOC = OCBE= 32=3，S AOB =SAOC +SBOC = 23如图，已知 E
31、、F 分别是ABCD 的边 BC、AD 上的点，且 BE=DF（1）求证：四边形 AECF 是平行四边形；（2）若 BC=10，BAC=90，且四边形 AECF 是菱形，求 BE 的长【考点】平行四边形的判定与性质；菱形的性质【分析】 （1）首先由已知证明 AFEC，BE=DF ，推出四边形 AECF 是平行四边形 （2）由已知先证明 AE=BE，即 BE=AE=CE，从而求出 BE 的长【解答】 （1）证明：四边形 ABCD 是平行四边形，ADBC，且 AD=BC，AFEC，BE=DF ，AF=EC，四边形 AECF 是平行四边形（2）解：四边形 AECF 是菱形，第 23 页（共 35 页
32、）AE=EC ，1=2，3=902，4=90 1，3=4，AE=BE，BE=AE=CE= BC=524学习了数据的收集、整理与表示之后，某小组同学对本校“自主选修活动课”比较感兴趣，他们以问卷的形式随机调查了 40 名学生的选课情况（每人只能选一项） ，并统计如下：科目 篮球 围棋 剪纸 舞台剧 茶艺 交谊舞 其它课计数 正正 正 正一 正一（1）请选择一种统计图将上表中的结果表示出来；（2）该校共有 500 名学生，请估计选修篮球课的人数；并说明你估计的理由；（3）谈谈你对该校“自主选修活动课”的科目设置有哪些建议？【考点】用样本估计总体；统计图的选择【分析】 （1）根据统计给出的数据画出条
33、形统计图即可；（2）用该校的总人数乘以修篮球课的人数所占的百分比即可得出答案；（3）根据统计给出的数据给出合理的建议即可，答案不唯一【解答】解：（1）根据题意画图如下：第 24 页（共 35 页）（2）根据题意得：500 =125（人） 答：选修篮球课的人数是 125 人；理由是：样本估计总体；（3）该校“自主选修活动课”的科目应多设置些围棋课，学生学围棋的较少25如图，D 为O 上一点，点 C 在直径 BA 的延长线上，且CDA= CBD（1）求证：CD 是O 的切线；（2）过点 B 作O 的切线交 CD 的延长线于点 E，若 BC=6，tanCDA= ，求BE 的长【考点】切线的判定与性质
34、；圆周角定理；相似三角形的判定与性质【分析】 （1）连 OD，OE，根据圆周角定理得到ADO+1=90，而CDA=CBD，CBD=1，于是CDA+ADO=90；（2）根据切线的性质得到 ED=EB，OEBD ，则 ABD=OEB，得到tanCDA=tanOEB= = ，易证 RtCDORt CBE，得到 = = = ，求得 CD，然后在 RtCBE 中，运用勾股定理可计算出 BE 的长第 25 页（共 35 页）【解答】 （1）证明：连 OD，OE，如图，AB 为直径，ADB=90 ，即ADO+1=90，又CDA= CBD，而CBD=1，1=CDA，CDA+ADO=90 ，即 CDO=90，C
35、D 是O 的切线；（2）解：EB 为O 的切线，ED=EB，OEDB ，ABD+DBE=90，OEB+DBE=90，ABD=OEB，CDA=OEB 而 tanCDA= ，tanOEB= = ，RtCDORtCBE， = = = ，CD= 6=4，在 RtCBE 中，设 BE=x，（x+4） 2=x2+62，解得 x= 即 BE 的长为 第 26 页（共 35 页）26我们把过三角形的一个顶点且能将这个三角形分割成两个等腰三角形的线段称为该三角形的“ 等腰线段” 例如：RtABC，取边 AB 的中点 D，线段 CD 就是ABC 的等腰线段（1）请分别画出下列三角形的等腰线段；（2）如图，在EFG
36、 中，若G=2 F，且EFG 有等腰线段，请直接写出F的度数的取值范围【考点】作图复杂作图；等腰三角形的性质【分析】 （1）利用三角形的等腰线段的定义画图；（2）设F=x ，则G=2x，讨论：如图 2，线段 EM 是等腰线段，则EM=EG，ME=MF，所以F=MEF=x ，EMG=G=2x ，根据三角形内角和得到2x90，则 x45 ；如图 3，GN 为等腰线段，第 27 页（共 35 页）则 NF=NG，GN=GE，所以F=NGF=x，E=ENG=2x，根据三角形内角和得到 x+2x+2x=180，解得 x=36，于是得到F 的度数的取值范围为 0x 45 【解答】解：（1）三角形的等腰线段
37、如图所示，（2）设F=x ，则G=2x，如图 2，线段 EM 是等腰线段，EMG 是等腰三角形，EM=EG，ME=MF，F= MEF=x，EMG=G=2x，2x90，x45 ；如图 3，GN 为等腰线段，NF=NG，GN=GE，F= NGF=x，E=ENG，EGN=x，ENG=2x，E=2x ，x+2x+2x=180 ，x=36，F 的度数的取值范围为 0x 45 第 28 页（共 35 页）27在平面直角坐标系 xOy 中，抛物线 y=ax22x 的对称轴为 x=1（1）求 a 的值及抛物线 y=ax22x 与 x 轴的交点坐标；（2）若抛物线 y=ax22x+m 与 x 轴有交点，且交点都
38、在点 A（ 4，0） ，B（1 ，0）之间，求 m 的取值范围【考点】抛物线与 x 轴的交点【分析】 （1）利用抛物线的对称轴方程得到 x= =1，解方程求出 a 即可得到抛物线的解析式为 y=x22x；然后解方程 x22x=0 可得到抛物线与 x 轴的交点坐标；（2）抛物线抛物线 y=x22x+m 由抛物线 y=x22x 上下平移|m|和单位得到，利第 29 页（共 35 页）用函数图象可得到当 x=1 时，y0，即1 2+m0；当 x=1 时，y0，即1+2+m0，然后解两个不等式求出它们的公共部分可得到 m 的范围【解答】解：（1）根据题意得 x= =1，解得 a=1，所以抛物线的解析式
39、为 y=x22x；当 y=0 时， x22x=0，解得 x1=0，x 2=2，所以抛物线与 x 轴的交点坐标为（ 2，0） ， （0，0） ；（2）抛物线抛物线 y=x22x+m 由抛物线 y=x22x 上下平移|m|和单位得到，而抛物线的对称轴为直线 x=1，抛物线 y=x22x+m 与 x 轴的交点都在点 A（ 4，0） ，B（1，0）之间，当 x=1 时，y 0 ，即1 2+m0，解得 m3；当 x=1 时，y 0，即1+2 +m0，解得 m1，m 的取值范围为1m328已知：在ABC 中， BAC=60 （1）如图 1，若 AB=AC，点 P 在ABC 内，且APC=150，PA=3，
40、PC=4，把APC 绕着点 A 顺时针旋转，使点 C 旋转到点 B，得到ADB，连结 DP依题意补全图 1；直接写出 PB 的长；（2）如图 2，若 AB=AC，点 P 在ABC 外，且 PA=3，PB=5，PC=4，求APC 的度数；（3）如图 3，若 AB=2AC，点 P 在ABC 内，且 PA= ，PB=5，APC=120 ，直接写出 PC 的长第 30 页（共 35 页）【考点】几何变换综合题【分析】 （1）由旋转的性质得到ADP 为等边三角形，从而判断出BPD 为直角三角形，根据勾股定理计算即可；（2）由旋转的性质得到DAP 是等边三角形，根据勾股定理得逆定理判断出BPD 为直角三角形，即可；（3）作出ABQACP，判断出APQ 为直角三角形，从而得到BPQ 为直角三角形，根据勾股定理计算即可【解答】解：（1）依题意补全图形，如图 1 所示，由旋转有，AD=AP，BD=PC，DAB=PAC，DAP=BAC=60，ADP 为等边三角形，DP=PA=3， ADP=60 ，ADB=APC=150，BDP=90，在 RtBDP 中，BD=4，DP=3，根据勾股定理得，PB=5；（2）如图 2，
