辽宁省沈阳市皇姑区2016年中考数学二模试卷含答案解析

《辽宁省沈阳市皇姑区2016年中考数学二模试卷含答案解析》由会员分享，可在线阅读，更多相关《辽宁省沈阳市皇姑区2016年中考数学二模试卷含答案解析（30页珍藏版）》请在七七文库上搜索。

1、第 1 页（共 30 页）2016 年辽宁省沈阳市皇姑区中考数学二模试卷一、 （下列各题的备选答案中，只有一个是正确的，每小题 2 分，满分 20 分）1下列运算正确的是（ ）A3 13=1 B （a 3） 2=a6 C =2 D|3|=32实数 ，3.14，0， 中，无理数共有（ ）A1 个 B2 个 C3 个 D4 个3下列说法正确的是（ ）A要了解人们对“ 低碳生活 ”的了解程度，宜采用普查方式B一组数据 5，5，6，7 的众数和中位数都是 5C必然事件发生的概率为 100%D若甲组数据的方差是 3.4，乙组数据的方差是 1.68，则甲组数据比乙组数据稳定4如图，ABC 和A 1B1C1

2、 是以点 O 为位似中心的位似三角形，若 C1 为 OC 的中点，AB=4，则 A1B1 的长为（ ）A1 B2 C4 D85下列各点中，在反比例函数 图象上的是（ ）A （2 ，1 ） B （ ，3） C （ 2，1） D （1，2）6如图，用尺规作出了 BFOA，作图痕迹中，弧 MN 是（ ）第 2 页（共 30 页）A以 B 为圆心，OD 长为半径的弧 B以 C 为圆心，CD 长为半径的弧C以 E 为圆心，DC 长为半径的弧 D以 E 为圆心，OD 长为半径的弧7不等式组 的整数解有（ ） 个A1 B2 C3 D48函数 y=kx+b（k、b 为常数， k0）的图象如图，则关于 x 的不

3、等式kx+b0 的解集为（ ）Ax 0 Bx0 Cx2 Dx29如图，平行线 a，b 被直线 c 所截，1=4238，则2 的度数为（ ）A15762 B13722 C13762 D472210如图，教师在小黑板上出示一道题，小华答：过点（3，0） ；小彬答：过点（4，3） ；小明答：a=1；小颖答：抛物线被 x 轴截得的线段长为 2你认为四人的回答中，正确的有（ ）A1 个 B2 个 C3 个 D4 个二、填空题（共 6 小题，每小题 3 分，满分 18 分）11计算 cos60= 12从 1，3，5 三个数中选取一个数作为 x，使二次根式 有意义的概率为 第 3 页（共 30 页）13如图

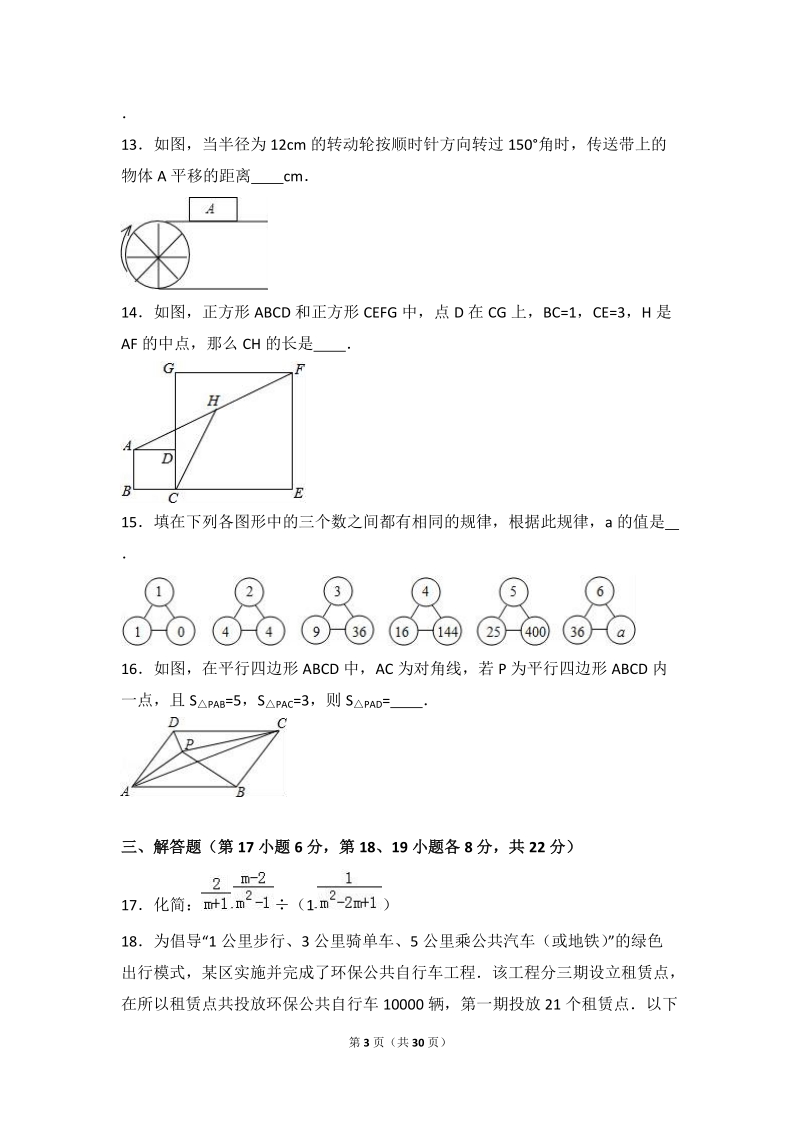
4、，当半径为 12cm 的转动轮按顺时针方向转过 150角时，传送带上的物体 A 平移的距离 cm14如图，正方形 ABCD 和正方形 CEFG 中，点 D 在 CG 上，BC=1，CE=3，H 是AF 的中点，那么 CH 的长是 15填在下列各图形中的三个数之间都有相同的规律，根据此规律，a 的值是 16如图，在平行四边形 ABCD 中，AC 为对角线，若 P 为平行四边形 ABCD 内一点，且 SPAB =5，S PAC =3，则 SPAD = 三、解答题（第 17 小题 6 分，第 18、19 小题各 8 分，共 22 分）17化简： （ 1 ）18为倡导“1 公里步行、3 公里骑单车、5

5、 公里乘公共汽车（或地铁） ”的绿色出行模式，某区实施并完成了环保公共自行车工程该工程分三期设立租赁点，在所以租赁点共投放环保公共自行车 10000 辆，第一期投放 21 个租赁点以下第 4 页（共 30 页）是根据相关数据绘制的自行车投放数量统计图（如图） ，以及投放的租赁点统计图（如图） ；”根据以上信息解答下列问题：（1）请根据以上信息，求第三期投放租赁点多少个？（2）直接补全条形统计图和扇形统计图；（3）该工程完成后，如果每辆自行车每天平均使用 4 次，每次骑行距离约3km，折算成驾车出行每 10km 消耗汽油 1 升，按照“消耗 1 升汽油=排 0.63kg碳”来计算，全区一天大约减

6、少碳排放 kg19某微博为了宣传邮票，推出时长为 5 秒的“转转盘、抢红包”活动如图，转盘被分为四等分，1、2、3、4 四个数字分别代表鸡、猴、鼠、羊四种生肖邮票，鸡年邮票面值“80 分”，其它邮票都是面值“1.20 元”，转动转盘后，指针每落在某个数字所在扇形一次，就抢到一个对应邮票面值的红包（假设每次转动后指针都不落在边界上） （1）如果在有效时间任意转动转盘一次，抢到 1.20 元红包的概率是 ；（2）如果在有效时间任意转动转盘两次，请用画树状图或列表法求两次共获得2.4 元红包的概率20如图，四边形 ABCD 中，BD 垂直平分 AC，垂足为点 F，E 为四边形 ABCD外一点，且AD

7、E=BAD，AEAC第 5 页（共 30 页）（1）求证：四边形 ABDE 是平行四边形；（2）如果 DA 平分BDE，AB=5，AD=6，求 AC 的长21列方程或方程组解应用题：在“春节”前夕，某花店用 13 000 元购进第一批礼盒鲜花，上市后很快销售一空根据市场需求情况，该花店又用 6 000 元购进第二批礼盒鲜花已知第二批所购鲜花的盒数是第一批所购鲜花的 ，且每盒鲜花的进价比第一批的进价少 10 元问第二批鲜花每盒的进价是多少元？22如图点 A、B、C 为O 上三点，AC 为O 的直径，AB CD，AC=CD连接 BD 交 AC 于点 E，交O 于点 F，AB= ，BC=3（1）求线

8、段 BD 的长；（2）线段 CF 的长为 （直接填空）23某商场有 A，B 两种商品，若买 2 件 A 商品和 1 件 B 商品，共需 80 元；若买 3 件 A 商品和 2 件 B 商品，共需 135 元（1）设 A，B 两种商品每件售价分别为 a 元、b 元，求 a、b 的值；（2）B 商品每件的成本是 20 元，根据市场调查：若按（1）中求出的单价销售，该商场每天销售 B 商品 100 件；若销售单价每上涨 1 元，B 商品每天的销售量就减少 5 件求每天 B 商品的销售利润 y（元）与销售单价（ x）元之间的函数关系？求销售单价为多少元时，B 商品每天的销售利润最大，最大利润是多少？2

9、4在正方形 ABCD 中，CD=5，BD 是一条对角线，动点 E 在直线 CD 上运动（不与点 C， D 不重合） ，连接 AE，平移ADE，使点 D 移动到点 C，得到第 6 页（共 30 页）BCF，过点 F 作 FGBD 于点 G，连接 AG，EG（1）如图，当点 E 在直线 CD 上时，线段 EF 的长为 （直接填空） （2）如图，当点 E 在线段 CD 的延长线上时，求证：AGD EGF；（3）点 E 在直线 CD 上运动过程中，当线段 DE 的长为 5 时，直接写出AGF的度数，不必说明理由25如图所示，已知抛物线 y=x2+4x+5 的顶点为 D，与 x 轴交于 A、B 两点（A

10、 左 B 右） ，与 y 轴交于 C 点，E 为抛物线上一点，且 C、E 关于抛物线的对称轴对称，作直线 AE（1）求直线 AE 的解析式；（2）在图中，若将直线 AE 沿 x 轴翻折后交抛物线于点 F，则点 F 的坐标为 （直接填空） ；（3）点 P 为抛物线上一动点，过点 P 作直线 PG 与 y 轴平行，交直线 AE 于点G，设点 P 的横坐标为 m，当 SPGE ：S BGE =2：3 时，直接写出所有符号条件的m 值，不必说明理由第 7 页（共 30 页）2016 年辽宁省沈阳市皇姑区中考数学二模试卷参考答案与试题解析一、 （下列各题的备选答案中，只有一个是正确的，每小题 2 分，满

11、分 20 分）1下列运算正确的是（ ）A3 13=1 B （a 3） 2=a6 C =2 D|3|=3【考点】幂的乘方与积的乘方；算术平方根；负整数指数幂【分析】结合选项分别进行幂的乘方和积的乘方、算术平方根、负整数指数幂的运算，然后选出正确选项【解答】解：A、3 13= ，原式计算错误，故本选项错误；B、 （a 3） 2=a6，原式计算正确，故本选项正确；C、 =2，原式计算错误，故本选项错误；D、|3|=3，原式计算错误，故本选项错误故选 B2实数 ，3.14，0， 中，无理数共有（ ）A1 个 B2 个 C3 个 D4 个【考点】无理数【分析】无理数就是无限不循环小数理解无理数的概念，一

12、定要同时理解有理数的概念，有理数是整数与分数的统称即有限小数和无限循环小数是有理数，而无限不循环小数是无理数由此即可判定选择项【解答】解： 是无理数，故选：A3下列说法正确的是（ ）A要了解人们对“ 低碳生活 ”的了解程度，宜采用普查方式第 8 页（共 30 页）B一组数据 5，5，6，7 的众数和中位数都是 5C必然事件发生的概率为 100%D若甲组数据的方差是 3.4，乙组数据的方差是 1.68，则甲组数据比乙组数据稳定【考点】概率的意义；全面调查与抽样调查；中位数；众数；方差；统计量的选择【分析】A、人口太多，难以普查；B、根据众数和中位数的定义解答即可；C、根据必然事件的概率为 1；D

13、、方差越大越不稳定，方差越小越稳定【解答】解：A、要了解人们对“ 低碳生活”的了解程度，宜采用抽样调查的方式，故本选项错误；B、数据 5，5，6，7 的众数是 5，中位数是 =5.5，故本选项错误；C、必然事件发生的概率为 100%，故本选项正确；D、若甲组数据的方差是 3.4，乙组数据的方差是 1.68，则乙组数据比甲组数据稳定，故本选项错误；故选 C4如图，ABC 和A 1B1C1 是以点 O 为位似中心的位似三角形，若 C1 为 OC 的中点，AB=4，则 A1B1 的长为（ ）A1 B2 C4 D8【考点】位似变换【分析】根据位似变换的性质得到 = ，B 1C1BC，再利用平行线分线第

14、 9 页（共 30 页）段成比例定理得到 = ，所以 = ，然后把 OC1= OC，AB=4 代入计算即可【解答】解：C 1 为 OC 的中点，OC 1= OC，ABC 和A 1B1C1 是以点 O 为位似中心的位似三角形， = ，B 1C1BC， = ， = ，即 =A 1B1=2故选 B5下列各点中，在反比例函数 图象上的是（ ）A （2 ，1 ） B （ ，3） C （ 2，1） D （1，2）【考点】反比例函数图象上点的坐标特征【分析】根据 y= 得 k=xy=2，所以只要点的横坐标与纵坐标的积等于2，就在函数图象上【解答】解：A、21=22，故不在函数图象上；B、 3=22，故不在函

15、数图象上；C、 （ 2）（ 1）=2 2 ，故不在函数图象上；第 10 页（共 30 页）D、 （1）2=2，故在函数图象上故选 D6如图，用尺规作出了 BFOA，作图痕迹中，弧 MN 是（ ）A以 B 为圆心，OD 长为半径的弧 B以 C 为圆心，CD 长为半径的弧C以 E 为圆心，DC 长为半径的弧 D以 E 为圆心，OD 长为半径的弧【考点】作图复杂作图【分析】作OBF=AOB，则可得到 BFOA ，于是利用基本作图可对四个选项进行判断【解答】解：以 B 点为圆心， OC 为半径作弧 EF 交 OB 于 E，然后以 E 点为圆心，CD 为半径画弧 MN，两弧相交于 F，则 BFOA 故选

16、 C7不等式组 的整数解有（ ） 个A1 B2 C3 D4【考点】一元一次不等式组的整数解【分析】先求出不等式组的解集，再确定符合题意的整数解的个数即可得出答案【解答】解：由 2x13，解得：x2 ，由 1，解得 x2，故不等式组的解为：2 x2，整数解为：2，1，0，1共有 4 个第 11 页（共 30 页）故选 D8函数 y=kx+b（k、b 为常数， k0）的图象如图，则关于 x 的不等式kx+b0 的解集为（ ）Ax 0 Bx0 Cx2 Dx2【考点】一次函数与一元一次不等式【分析】从图象上得到函数的增减性及与 x 轴的交点的横坐标，即能求得不等式 kx+b0 的解集【解答】解：函数

17、y=kx+b 的图象经过点（2，0） ，并且函数值 y 随 x 的增大而减小，所以当 x2 时，函数值小于 0，即关于 x 的不等式 kx+b0 的解集是 x2故选 C9如图，平行线 a，b 被直线 c 所截，1=4238，则2 的度数为（ ）A15762 B13722 C13762 D4722【考点】平行线的性质；度分秒的换算【分析】先由平行线的性质求出3 的度数，再由补角的定义即可得出结论【解答】解：ab， 1=4238，3=1=4238 ，2=1804238=13722故选 B第 12 页（共 30 页）10如图，教师在小黑板上出示一道题，小华答：过点（3，0） ；小彬答：过点（4，3）

18、 ；小明答：a=1；小颖答：抛物线被 x 轴截得的线段长为 2你认为四人的回答中，正确的有（ ）A1 个 B2 个 C3 个 D4 个【考点】抛物线与 x 轴的交点【分析】根据图上给出的条件是与 x 轴交于（1，0） ，叫我们加个条件使对称轴是 x=2，意思就是抛物线的对称轴是 x=2 是题目的已知条件，这样可以求出a、 b 的值，然后即可判断题目给出四个人的判断是否正确【解答】解：抛物线过（1，0） ，对称轴是 x=2， ，解得 a=1，b=4，y=x 24x+3，当 x=3 时，y=0，小华正确；当 x=4 时，y=3，小彬也正确，小明也正确；抛物线被 x 轴截得的线段长为 2，已知过点（

19、1 ，0） ，另一点为（1，0）或（ 3，0） ，对称轴为 y 轴或 x=2，此时答案不唯一，小颖错误第 13 页（共 30 页）故选 C二、填空题（共 6 小题，每小题 3 分，满分 18 分）11计算 cos60= 【考点】特殊角的三角函数值【分析】根据记忆的内容，cos60= 即可得出答案【解答】解：cos60= 故答案为： 12从 1，3，5 三个数中选取一个数作为 x，使二次根式 有意义的概率为 【考点】概率公式；二次根式有意义的条件【分析】由从 1，3，5 三个数中选取一个数作为 x，使二次根式 有意义的有 1，3，直接利用概率公式求解即可求得答案【解答】解：从 1，3，5 三个数

20、中选取一个数作为 x，使二次根式 有意义的有 1，3，使二次根式 有意义的概率为： 故答案为： 13如图，当半径为 12cm 的转动轮按顺时针方向转过 150角时，传送带上的物体 A 平移的距离 10 cm【考点】弧长的计算；平移的性质【分析】根据题意可知转过的弧长与传送带上的物体 A 平移的距离相等，只要求出转过的弧长即可解答本题第 14 页（共 30 页）【解答】解：由题意可得，半径为 12cm 的转动轮按顺时针方向转过 150角的弧长为： =10（ cm） ，由题意可知转过的弧长与传送带上的物体 A 平移的距离相等，故答案为：1014如图，正方形 ABCD 和正方形 CEFG 中，点 D

21、 在 CG 上，BC=1，CE=3，H 是AF 的中点，那么 CH 的长是 【考点】正方形的性质；直角三角形斜边上的中线；勾股定理【分析】根据正方形的性质求出 AB=BC=1，CE=EF=3 ，E=90，延长 AD 交 EF于 M，连接 AC、CF，求出 AM=4，FM=2，AMF=90，根据正方形性质求出ACF=90，根据直角三角形斜边上的中线性质求出 CH= AF，根据勾股定理求出 AF 即可【解答】解：正方形 ABCD 和正方形 CEFG 中，点 D 在 CG 上，BC=1 ，CE=3，AB=BC=1，CE=EF=3， E=90，延长 AD 交 EF 于 M，连接 AC、CF，则 AM=

22、BC+CE=1+3=4，FM=EF AB=31=2，AMF=90，四边形 ABCD 和四边形 GCEF 是正方形，ACD=GCF=45，ACF=90，H 为 AF 的中点，CH= AF，第 15 页（共 30 页）在 RtAMF 中，由勾股定理得：AF= = =2 ，CH= ，故答案为： 15填在下列各图形中的三个数之间都有相同的规律，根据此规律，a 的值是 900 【考点】规律型：图形的变化类；规律型：数字的变化类【分析】根据已知数据即可得出，最下面一行数字变化规律，进而得出答案【解答】解：根据下面一行数字变化规律为：14=4，49=36，916=144，1625=400，2536=a=90

23、0，故答案为：90016如图，在平行四边形 ABCD 中，AC 为对角线，若 P 为平行四边形 ABCD 内一点，且 SPAB =5，S PAC =3，则 SPAD = 2 第 16 页（共 30 页）【考点】平行四边形的性质【分析】假设 P 点到 AB 的距离是 h1，假设 P 点到 DC 的距离是 h2，根据三角形的面积公式求出PAB 和PDC 的面积和，推出 SADC =SPAB +SPDC =5+SPDC 和SPAD =SADC SPDC SPAC ，代入即可求出答案【解答】解：四边形 ABCD 是平行四边形，AB=DC，假设 P 点到 AB 的距离是 h1，假设 P 点到 DC 的距

24、离是 h2，S PAB = ABh1，S PDC = DCh2，S PAB +SPDC = （ABh 1+DCh2）= DC（h 1+h2） ，h 1+h2 正好是 AB 到 DC 的距离，S PAB +SPDC = S 平行四边形 ABCD=SABC =SADC ，即 SADC =SPAB +SPDC =5+SPDC ，S PAD =SADC SPDC SPAC ，S PAC =53=2，故答案为：2三、解答题（第 17 小题 6 分，第 18、19 小题各 8 分，共 22 分）17化简： （ 1 ）【考点】分式的混合运算【分析】原式第二项括号中通分并利用同分母分式的减法法则计算，同时利用

25、除法法则变形，约分后两项通分并利用同分母分式的减法法则计算即可得到结果第 17 页（共 30 页）【解答】解：原式= = = = 18为倡导“1 公里步行、3 公里骑单车、5 公里乘公共汽车（或地铁） ”的绿色出行模式，某区实施并完成了环保公共自行车工程该工程分三期设立租赁点，在所以租赁点共投放环保公共自行车 10000 辆，第一期投放 21 个租赁点以下是根据相关数据绘制的自行车投放数量统计图（如图） ，以及投放的租赁点统计图（如图） ；”根据以上信息解答下列问题：（1）请根据以上信息，求第三期投放租赁点多少个？（2）直接补全条形统计图和扇形统计图；（3）该工程完成后，如果每辆自行车每天平均

26、使用 4 次，每次骑行距离约3km，折算成驾车出行每 10km 消耗汽油 1 升，按照“消耗 1 升汽油=排 0.63kg第 18 页（共 30 页）碳”来计算，全区一天大约减少碳排放 7560 kg【考点】条形统计图；用样本估计总体；扇形统计图；加权平均数【分析】 （1）由第一期共投放 21 个租赁点，所占百分比为 7%，求出投放租赁点的总个数，再根据第三期投放租赁点所占百分比为 66%，列式计算即可求解；（2）根据条形图求出第二期投放环保公共自行车的数量，根据扇形图得出第三期投放自行车租赁点所占百分比，进而补全条形统计图和扇形统计图；（3）先求出 10000 辆自行车一天骑行距离，再根据每

27、 10km 消耗汽油 1 升，消耗 1 升汽油=排 0.63kg 碳，即可求解【解答】解：（1）217%=300（个） ，300（17% 27%）=198（个） 答：第三期投入使用的公共自行车站点有 198 个；（2）第二期投放环保公共自行车的数量为：100001000 6000=3000（辆） ，第三期投放自行车租赁点所占百分比为：17% 27%=66%补全条形统计图和扇形统计图如图：（3） ）每辆自行车每天平均使用 4 次，每次骑行距离约 3km，共投放环保公共自行车 10000 辆，一天骑行距离为 3410000=120000（km） ，每 10km 消耗汽油 1 升，消耗 1 升汽油=

28、 排 0.63kg 碳，第 19 页（共 30 页）全区一天大约减少碳排放 0.6312000010=7560（kg） ，故答案为：756019某微博为了宣传邮票，推出时长为 5 秒的“转转盘、抢红包”活动如图，转盘被分为四等分，1、2、3、4 四个数字分别代表鸡、猴、鼠、羊四种生肖邮票，鸡年邮票面值“80 分”，其它邮票都是面值“1.20 元”，转动转盘后，指针每落在某个数字所在扇形一次，就抢到一个对应邮票面值的红包（假设每次转动后指针都不落在边界上） （1）如果在有效时间任意转动转盘一次，抢到 1.20 元红包的概率是 ；（2）如果在有效时间任意转动转盘两次，请用画树状图或列表法求两次共获

29、得2.4 元红包的概率【考点】列表法与树状图法；概率公式【分析】 （1）直接利用概率公式计算；（2）画树状图展示所有 16 种等可能的结果数，再找出两次共获得 2.4 元红包的结果数，然后根据概率公式求解【解答】解：（1）在有效时间任意转动转盘一次，抢到 1.20 元红包的概率= ；故答案为 ；（2）画树状图为：共有 16 种等可能的结果数，其中两次共获得 2.4 元红包的结果数为 12，所以两次共获得 2.4 元红包的概率= = 20如图，四边形 ABCD 中，BD 垂直平分 AC，垂足为点 F，E 为四边形 ABCD第 20 页（共 30 页）外一点，且ADE=BAD，AEAC（1）求证：

30、四边形 ABDE 是平行四边形；（2）如果 DA 平分BDE，AB=5，AD=6，求 AC 的长【考点】菱形的判定与性质；勾股定理；平行四边形的判定【分析】 （1）由平行四边形的判定定理：两组对边分别平行得到结论；（2）由角平分线、等量代换得到角相等，由等角对等边得到 BD=AB=5，根据勾股定理列方程求解【解答】 （1）证明：ADE=BAD，ABDE，AE AC，BDAC，AE BD，四边形 ABDE 是平行四边形；（2）解：DA 平分BDE，AED= BDA，BAD=BDA ，BD=AB=5，设 BF=x，则 DF=5x，AD 2DF2=AB2BF2，6 2（5 x） 2=52x2，x=

31、，AF= = ，第 21 页（共 30 页）AC=2AF= 21列方程或方程组解应用题：在“春节”前夕，某花店用 13 000 元购进第一批礼盒鲜花，上市后很快销售一空根据市场需求情况，该花店又用 6 000 元购进第二批礼盒鲜花已知第二批所购鲜花的盒数是第一批所购鲜花的 ，且每盒鲜花的进价比第一批的进价少 10 元问第二批鲜花每盒的进价是多少元？【考点】分式方程的应用【分析】可设第二批鲜花每盒的进价是 x 元，根据等量关系：第二批所购鲜花的盒数是第一批所购鲜花的 ，列出方程求解即可【解答】解：设第二批鲜花每盒的进价是 x 元，依题意有= ，解得 x=120，经检验：x=120 是原方程的解，

32、答：第二批鲜花每盒的进价是 120 元22如图点 A、B、C 为O 上三点，AC 为O 的直径，AB CD，AC=CD连接 BD 交 AC 于点 E，交O 于点 F，AB= ，BC=3（1）求线段 BD 的长；（2）线段 CF 的长为 （直接填空）【考点】相似三角形的判定与性质；圆周角定理【分析】 （1）根据直径所对的圆周角是直角可得ABC=90，然后利用勾股定理列式求出 AC，再根据两直线平行，同旁内角互补求出BCD=90，然后利用勾股定理列式计算即可得解；第 22 页（共 30 页）（2）连接 AF，根据直径所对的圆周角是直角可得AFC=90，再根据同弧所对的圆周角相等可得CBD=CAF，

33、然后求出ACF 和BDC 相似，利用相似三角形对应边成比例列式计算即可得解【解答】解：（1）AC 为O 的直径，ABC=90 ，在 RtABC 中，由勾股定理得， AC= = =4，AC=CD，CD=4，ABCD，BCD=180ABC=18090=90，在 RtBCD 中，由勾股定理得，BD= = =5；（2）如图，连接 AF，AC 为O 的直径，AFC=90，BCD=AFC=90，又CBD=CAF（同弧所对的圆周角相等） ，ACF BDC， = ，即 = ，解得 CF= 故答案为： 第 23 页（共 30 页）23某商场有 A，B 两种商品，若买 2 件 A 商品和 1 件 B 商品，共需

34、80 元；若买 3 件 A 商品和 2 件 B 商品，共需 135 元（1）设 A，B 两种商品每件售价分别为 a 元、b 元，求 a、b 的值；（2）B 商品每件的成本是 20 元，根据市场调查：若按（1）中求出的单价销售，该商场每天销售 B 商品 100 件；若销售单价每上涨 1 元，B 商品每天的销售量就减少 5 件求每天 B 商品的销售利润 y（元）与销售单价（ x）元之间的函数关系？求销售单价为多少元时，B 商品每天的销售利润最大，最大利润是多少？【考点】二次函数的应用；二元一次方程组的应用【分析】 （1）根据题意列方程组即可得到结论；（2）由题意列出关于 x，y 的方程即可；把函数

35、关系式配方即可得到结果【解答】解：（1）根据题意得： ，解得： ；（2）由题意得：y=（x 20） 【100 5（x 30） 】y= 5x2+350x5000，y=5x 2+350x5000=5（x35） 2+1125，当 x=35 时，y 最大 =1125，销售单价为 35 元时，B 商品每天的销售利润最大，最大利润是 1125 元24在正方形 ABCD 中，CD=5，BD 是一条对角线，动点 E 在直线 CD 上运动第 24 页（共 30 页）（不与点 C， D 不重合） ，连接 AE，平移ADE，使点 D 移动到点 C，得到BCF，过点 F 作 FGBD 于点 G，连接 AG，EG（1）

36、如图，当点 E 在直线 CD 上时，线段 EF 的长为 5 （直接填空） （2）如图，当点 E 在线段 CD 的延长线上时，求证：AGD EGF；（3）点 E 在直线 CD 上运动过程中，当线段 DE 的长为 5 时，直接写出AGF的度数，不必说明理由【考点】四边形综合题【分析】 （1）根据 DE=CF，可以推出 EF=CD，由此即可解决问题（2）欲证明AGDEGF ，只要证明ADG=EFG=45，DG=FG，AD=EF 即可（3）AGF 的度数为 60或 120，分两种情形见图，分别求解即可【解答】 （1）解：如图中，BCF 是由ADE 平移所得，DE=CF，EF=CD=5，故答案为 5（2

37、）证明：四边形 ABCD 是正方形，CD=AD=EF，ADG=FDG=45，FGBD，DFG=FDG=45 ，DG=GF，在AGD 和 EGF 中，第 25 页（共 30 页）AGD EGF（3）AGF 的度数为 60或 120理由；如图中，在 RTAED 中，ADE=90， ED=5 ，AD=5 ，tanAED= = ，AED=30 ，由（2）可知AGDEGF，EGF=AGD ，EG=AG，EGA=FCD=90，GEA=EAG=45，DEG=15 ，DFG=FEG+FGE，EGF=AGD=30，AGF=90AGD=60 ，如图中，同理可证AGD=EGF=30 ，可得AGF=AGD+DGF=1

38、20 AGF 的度数为 60或 120第 26 页（共 30 页）25如图所示，已知抛物线 y=x2+4x+5 的顶点为 D，与 x 轴交于 A、B 两点（A 左 B 右） ，与 y 轴交于 C 点，E 为抛物线上一点，且 C、E 关于抛物线的对称轴对称，作直线 AE（1）求直线 AE 的解析式；（2）在图中，若将直线 AE 沿 x 轴翻折后交抛物线于点 F，则点 F 的坐标为 （6，7） （直接填空） ；（3）点 P 为抛物线上一动点，过点 P 作直线 PG 与 y 轴平行，交直线 AE 于点G，设点 P 的横坐标为 m，当 SPGE ：S BGE =2：3 时，直接写出所有符号条件的m 值

39、，不必说明理由【考点】二次函数综合题【分析】 （1）根据抛物线的解析式可找出该抛物线的对称轴为 x=2 以及点A、B 、C 的坐标，由点 C 的坐标结合 C、E 关于抛物线的对称轴对称，可求出点第 27 页（共 30 页）E 的坐标，设直线 AE 的解析式为 y=kx+b，由点 A、E 的坐标利用待定系数法即可求出直线 AE 的解析式；（2）设直线 AF 的解析式为 y=ax+c，找出点 E 关于 x 轴对称的点的坐标，利用该点和 A 点坐标利用待定系数法即可求出直线 AF 的解析式，再联立直线 AF 以及抛物线的解析式成方程组，解方程组即可求出点 F 的坐标；（3）由点 P 的横坐标以及点

40、P 在抛物线上即可找出点 P 的坐标，利用点到直线的距离公式分别求出点 P、B 到直线 AE 的距离，再根据同底三角形的面积关系即可得出关于 m 的含绝对值符号的一元二次方程，解方程即可得出结论【解答】解：（1）抛物线的解析式为 y=x2+4x+5，该抛物线的对称轴为：x= =2令 y=x2+4x+5 中 x=0，则 y=5，点 C 的坐标为（ 0，5 ） C 、E 关于抛物线的对称轴对称，点 E 的坐标为（220，5） ，即（4，5） 令 y=x2+4x+5 中 y=0，则x 2+4x+5=0，解得：x 1=1，x 2=5，点 A 的坐标为（1，0） 、点 B 的坐标为（5，0） 设直线 A

41、E 的解析式为 y=kx+b，将点 A（1 ，0） 、E （4，5）代入 y=kx+b 中，得： ，解得： ，直线 AE 的解析式为 y=x+1（2）设直线 AF 的解析式为 y=ax+c，点 E 的坐标为（4，5） ，点 E 关于 x 的对称点的坐标为（4，5） ，将点（1，0） 、 （4，5）代入 y=ax+c 中，第 28 页（共 30 页）得： ，解得： ，直线 AF 的解析式为 y=x1联立直线 AF 与抛物线的解析式成方程组： ，解得： ，或 ，点 F 的坐标为（6，7） ，故答案为（6，7） （3）点 P 的横坐标为 m，且点 P 在抛物线 y=x2+4x+5 的图象上，点 P 的坐标为（ m， m2+4m+5） 点 B 的坐标为（5，0） ，直线 AE 的解析式为 y=x+1，即 xy+1=0，点 P 到直线 AE 的距离 d1= ；点 B 到直线 AE 的距离 d2= PGE 与BGE 有共同的底边 GE，且 SPGE ：S BGE =2：3，d 1：d 2=2：3，即 ： =2：3，整理得：|m 23m4|=4，解得：m 1=0，m 2=3，m 3= ，m 4= ，第 29 页（共 30 页）当 SPGE ：S BGE =2：3 时，符号条件的 m 值为 0、3、 和 第 30 页（共 30 页）2017 年 3 月 1 日