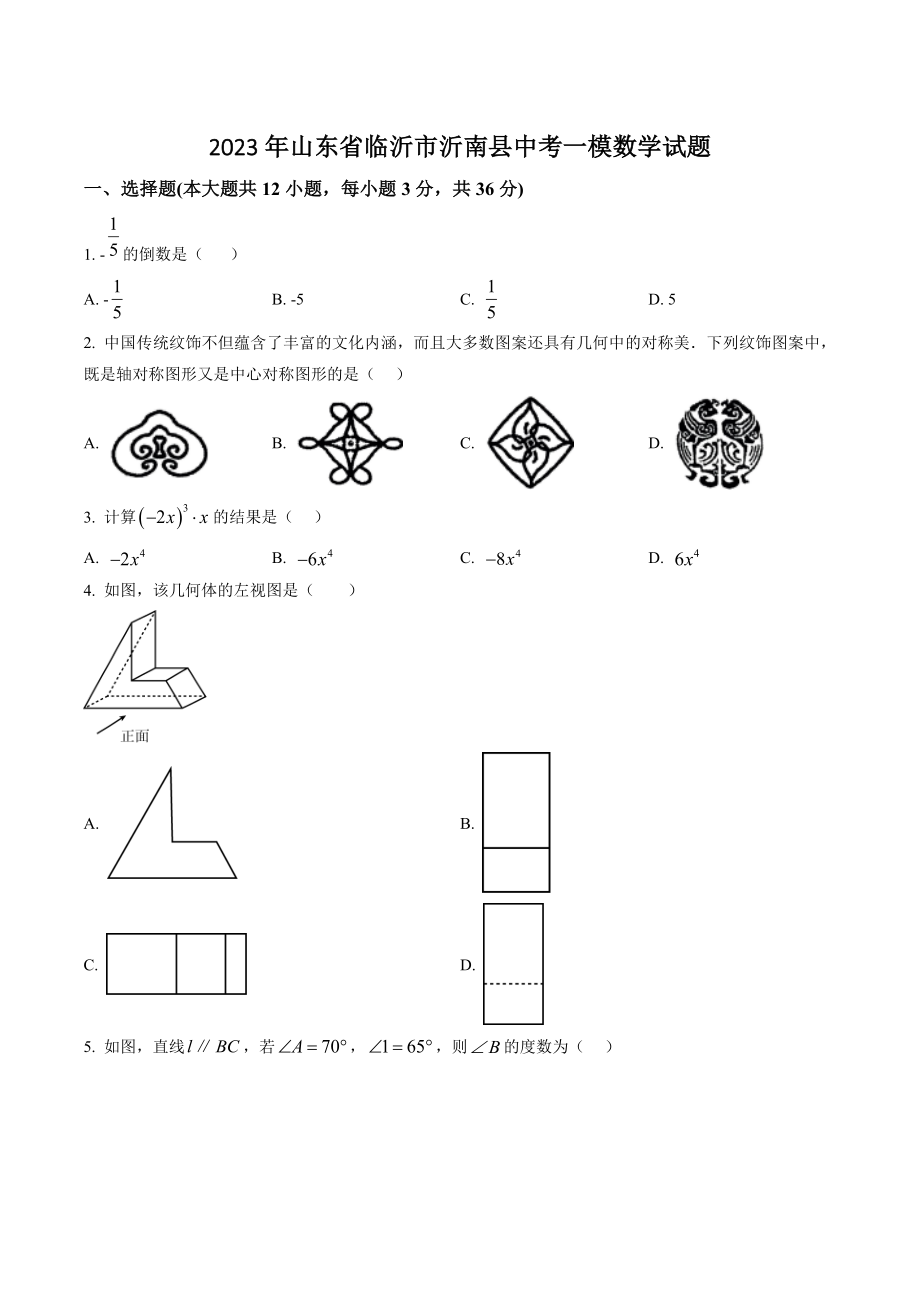
1、2023年山东省临沂市沂南县中考一模数学试题一、选择题(本大题共12小题，每小题3分，共36分) 1. -的倒数是（ ）A. -B. -5C. D. 52. 中国传统纹饰不但蕴含了丰富的文化内涵，而且大多数图案还具有几何中的对称美下列纹饰图案中，既是轴对称图形又是中心对称图形的是（ ）A. B. C. D. 3. 计算的结果是（ ）A. B. C. D. 4. 如图，该几何体的左视图是（ ）A. B. C. D. 5. 如图，直线，若，则的度数为（ ）A. B. C. D. 6. 不等式的解集在数轴上表示正确的是（ ）A. B. C. D. 7. 估计的值应在( )A. 1和2之间B. 2和3
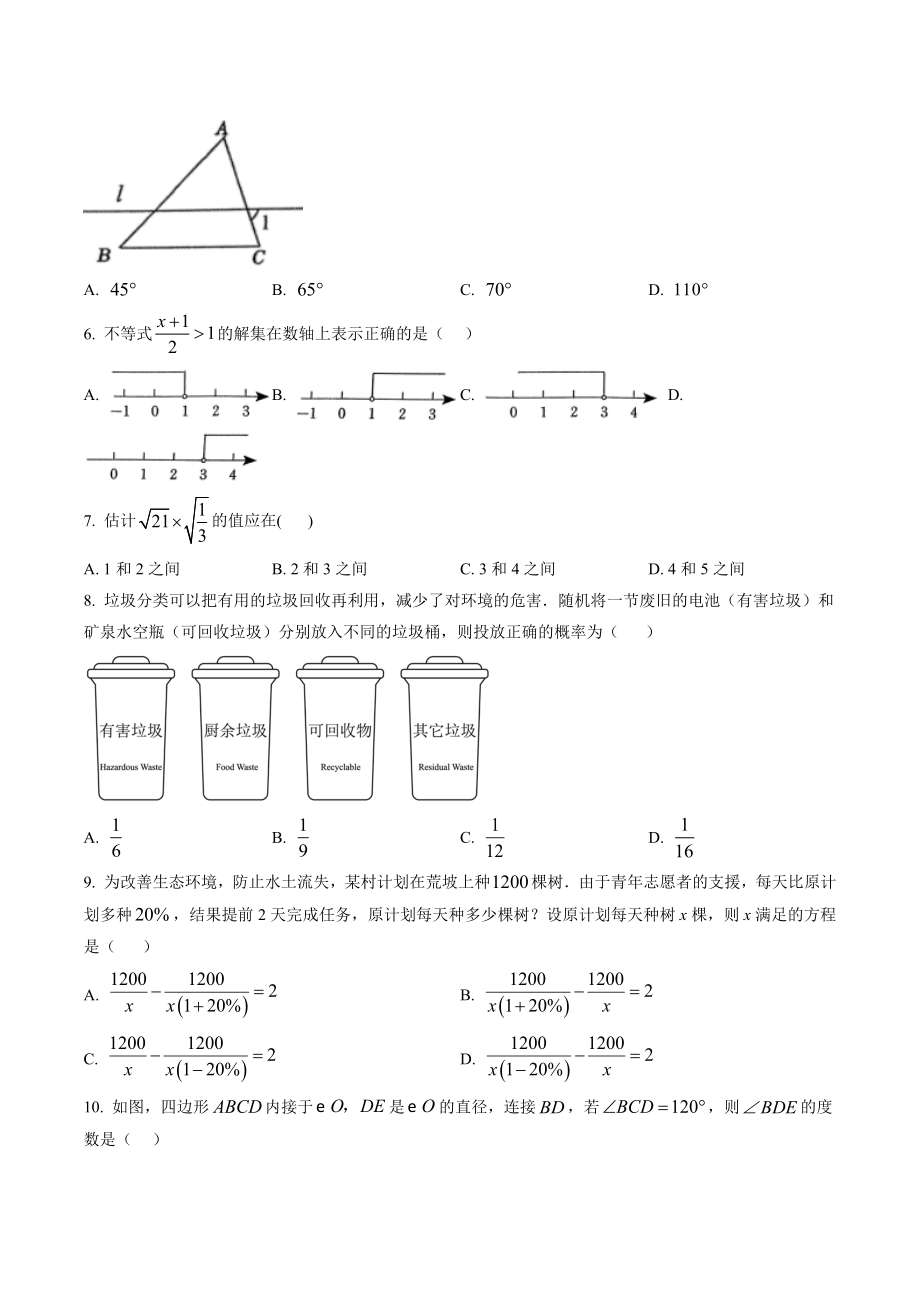
2、之间C. 3和4之间D. 4和5之间8. 垃圾分类可以把有用的垃圾回收再利用，减少了对环境的危害随机将一节废旧的电池（有害垃圾）和矿泉水空瓶（可回收垃圾）分别放入不同的垃圾桶，则投放正确的概率为（ ）A. B. C. D. 9. 为改善生态环境，防止水土流失，某村计划在荒坡上种棵树由于青年志愿者的支援，每天比原计划多种，结果提前2天完成任务，原计划每天种多少棵树？设原计划每天种树x棵，则x满足的方程是（ ）A. B. C. D. 10. 如图，四边形内接于是的直径，连接，若，则的度数是（ ）A. B. C. D. 11. 画二次函数的图象时，列表如下：x1234y010-3关于此函数有下列说法
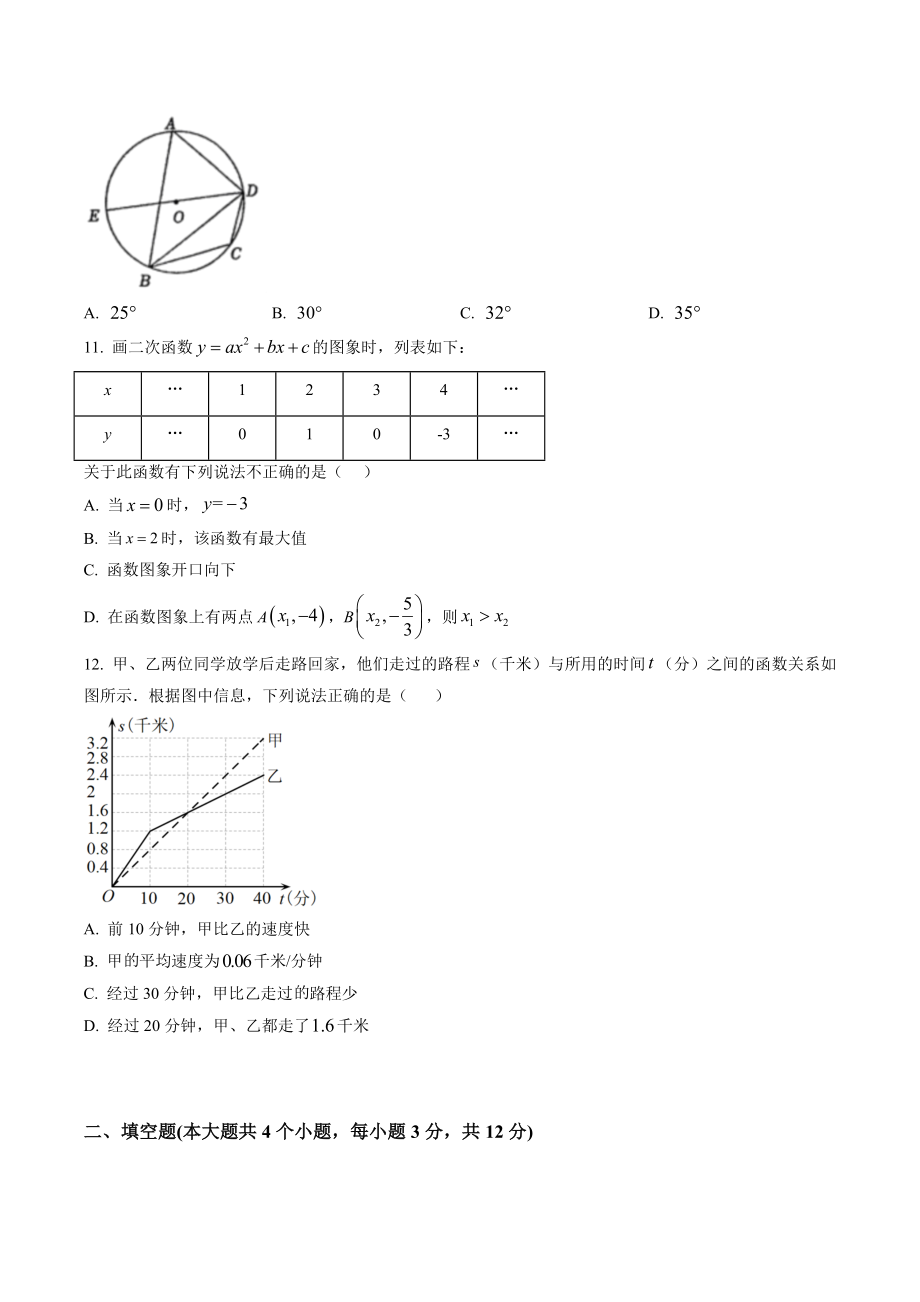
3、不正确的是（ ）A. 当时，B. 当时，该函数有最大值C. 函数图象开口向下D. 在函数图象上有两点A，B，则12. 甲、乙两位同学放学后走路回家，他们走过的路程（千米）与所用的时间（分）之间的函数关系如图所示根据图中信息，下列说法正确的是（ ）A. 前10分钟，甲比乙的速度快B. 甲平均速度为千米/分钟C. 经过30分钟，甲比乙走过路程少D. 经过20分钟，甲、乙都走了千米二、填空题(本大题共4个小题，每小题3分，共12分)13 分解因式： _ 14. 已知二元一次方程组，则的值为_15. 如图，已知RtABC的边BC在x轴上，且A（1，2），B（-2，0）若将ABC平移，使点B落在点A处，
4、则点C的对应点的坐标为_16. 如图，矩形中，相交于点O，过点B作交于点F，交与点M，过点D作交于点E，交于点N，连接，则下列结论：；当时，四边形是菱形其中，正确结论的个数是_三、解答题(本大题共7小题，共72分)17. 计算：（1）；（2）18. 某校为加强学生的安全意识，对七、八年级全体学生进行了安全知识测试，现要了解学生掌握安全知识的具体情况，从七、八年级各随机抽取50名学生进行数据分析，并对成绩(百分制)进行整理、描述和分析部分信息如下：A如图是所抽取的七年级成绩频数分布直方图B所抽取的七年级成绩在这一组的是：70，72，74，75，76，76，77，77，77，78，79C七、八年级
5、成绩的平均数、中位数如下：年级平均数中位数七76.9m八79.279.5根据以上信息，回答下列问题：（1）表中m的值为：_；（2）在这次测试中，七年级学生甲与八年级学生乙的成绩都是79分，请判断两位学生在各自年级的排名谁更靠前，并说明理由；（3）该校七年级学生有500人，请估计七年级成绩超过平均分的人数19. 越来越多太阳能路灯的使用，既点亮了城市的风景，也是我市积极落实节能环保的举措，某校学生开展综合实践活动，测量太阳能路灯电池板离地面的高度，如图，已知测倾器的高度为1.5米，在测点A处安置测倾器，测得点M的仰角，在与点A相距3米的测点D处安置测倾器，测得点M的仰角(点A，D与N在一条直线上
6、)求电池板离地面的高度的长(结果取整数，参考数据：，)20. 已知蓄电池的电压为定值，使用蓄电池时，电流I（A）与电阻R（）是反比例函数关系，当电阻R9时，电流I4A（1）求I关于R的函数表达式和自变量R的取值范围；（2）画出所求函数图像；（3）若以此蓄电池为电源的用电器的限制电流不超过10A，求用电器可变电阻应控制在什么范围？21. 如图，AB是O的直径，AC是O的切线，切点为A，BC交O于点D，点E是AC的中点（1）试判断直线DE与O的位置关系，并说明理由（2）若O半径为2，B60，求图中阴影部分的面积22. 科技创新是发展第一动力某科研公司向市场推出了一款创新产品，该产品的成本价格是40
7、元/件，销售价格y(元/件)与销售量x(件)之间满足一次函数关系，部分数据如下表：x（件）101520（元/件）585756（1）求y与x之间的函数关系式；（2）求销售利润w(元)关于销售量x(件)的函数解析式，当销售量为多少时，销售利润最大？最大值是多少？（3）为了保证销售利润不低于420元，求该产品的销售价格的取值范围23. 正方形 ，点E为平面内一点，连接，将绕点B顺时针旋转得到 ，连接，已知点M为的中点，连接（1）如图1，若点E为边边上一点，补全图形；判断并证明线段和的数量关系（2）如图2，若点E是的内部一点，（1）中线段和的数量关系是否仍然成立，如果成立，请证明；如果不成立，请说明理
8、由2023年山东省临沂市沂南县中考一模数学试题一、选择题(本大题共12小题，每小题3分，共36分) 1. -的倒数是（ ）A. -B. -5C. D. 5【答案】B【解析】【分析】倒数：乘积是1的两数互为倒数据此可得答案【详解】解：-的倒数是-5故选：B【点睛】本题考查了倒数，掌握倒数的定义是解答本题的关键2. 中国传统纹饰不但蕴含了丰富的文化内涵，而且大多数图案还具有几何中的对称美下列纹饰图案中，既是轴对称图形又是中心对称图形的是（ ）A. B. C. D. 【答案】B【解析】【分析】根据轴对称图形、中心对称图形定义逐项判断即可中心对称是指把一个图形绕着某一点旋转180度，如果它能够与另一个
9、图形重合，那么就说这两个图形关于这个点对称或中心对称；把一个图形沿着某一条直线折叠，如果它能够与另一个图形完全重合，称这两个图形为轴对称【详解】解：A、是轴对称图形，不是中心对称图形，故选项错误，不符合题意；B、既是轴对称图形，也是中心对称图形，故选项正确，符合题意；C、不是轴对称图形，是中心对称图形，故选项错误，不符合题意；D、既不是轴对称图形，也不是中心对称图形，故选项错误，不符合题意；故选：B【点睛】本题考查了轴对称图形和中心对称图形的定义，解题的关键是掌握轴对称图形、中心对称图形的定义3. 计算的结果是（ ）A. B. C. D. 【答案】C【解析】【分析】先算积的乘方，然后计算同底数
10、的幂的乘法【详解】,故选C【点睛】本题考查幂的运算，掌握运算法则是解题的关键4. 如图，该几何体的左视图是（ ）A. B. C. D. 【答案】D【解析】【分析】画出从左面看到的图形即可【详解】解：该几何体的左视图是一个长方形，并且有一条隐藏的线用虚线表示，如图所示：，故选：D【点睛】本题考查三视图，具备空间想象能力是解题的关键，注意看不见的线要用虚线画出5. 如图，直线，若，则的度数为（ ）A. B. C. D. 【答案】A【解析】【分析】利用平行线的性质得到，再利用三角形的内角和定理解题即可【详解】解：，故选A【点睛】本题考查平行线的性质和三角形的内角和定理，掌握三角形的内角和定理是解题的
11、关键6. 不等式的解集在数轴上表示正确的是（ ）A. B. C. D. 【答案】B【解析】【分析】先求出不等式的解集，然后把解集表示在数轴上即可【详解】解：，；把解集表示在数轴上，则故选：B【点睛】本题考查了解一元一次不等式，以及把解集表示在数轴上，解题的关键是正确的求出不等式的解集7. 估计的值应在( )A. 1和2之间B. 2和3之间C. 3和4之间D. 4和5之间【答案】B【解析】【分析】先根据二次根式乘法运算法则计算得到，再根据无理数估算由，得到，从而确定答案【详解】解：，又，即的值在2和3之间，故选：B【点睛】本题考查二次根式的运算及无理数估算，掌握二次根式乘法运算法则及无理数估算方
12、法是解决问题的关键8. 垃圾分类可以把有用的垃圾回收再利用，减少了对环境的危害随机将一节废旧的电池（有害垃圾）和矿泉水空瓶（可回收垃圾）分别放入不同的垃圾桶，则投放正确的概率为（ ）A. B. C. D. 【答案】C【解析】【分析】可回收垃圾、餐厨垃圾、有害垃圾和其他垃圾对应的垃圾桶分别用A，B，C，D表示，设两件不同垃圾为a、b，画出树状图，由概率公式即可得出答案【详解】解：可回收垃圾、餐厨垃圾、有害垃圾和其他垃圾对应的垃圾桶分别用A，B，C，D表示，设两袋不同垃圾为a、b，画树状图如图：共有12个等可能的结果，两件不同垃圾随机投入进两个不同的垃圾桶，投放正确的结果有1个，两件不同垃圾随机投
13、入进两个不同的垃圾桶，投放正确的概率为，故选：C【点睛】此题考查了树状图法与列表法求概率此题难度不大，解题的关键是根据题意画出树状图或列出表格，注意树状图法与列表法可以不重不漏的表示出所有等可能的结果，注意用到的知识点为：概率=所求情况数与总情况数之比9. 为改善生态环境，防止水土流失，某村计划在荒坡上种棵树由于青年志愿者的支援，每天比原计划多种，结果提前2天完成任务，原计划每天种多少棵树？设原计划每天种树x棵，则x满足的方程是（ ）A. B. C. D. 【答案】A【解析】【分析】设原计划每天种树x棵，则原计划需要天，实际需要天，由此建立方程即可【详解】解：设原计划每天种树x棵，由题意得，故
14、选A【点睛】本题主要考查了从实际问题中抽象出分式方程，正确理解题意找到等量关系是解题的关键10. 如图，四边形内接于是的直径，连接，若，则的度数是（ ）A. B. C. D. 【答案】B【解析】【分析】首先利用圆内接四边形的性质和的度数求得的度数，然后利用直径所对的圆周角是直角确定，然后利用直角三角形的两个锐角互余求得答案即可【详解】解：连，四边形内接与，为直径，故选：B【点睛】本题考查了圆内接四边形的性质及圆周角定理的知识，解题的关键是了解圆内接四边形的对角互补11. 画二次函数的图象时，列表如下：x1234y010-3关于此函数有下列说法不正确的是（ ）A. 当时，B. 当时，该函数有最大
15、值C. 函数图象开口向下D. 在函数图象上有两点A，B，则【答案】D【解析】【分析】先由表中数据可知，随的增大先增大后减小，得到函数图象开口向下；利用时，或，得到函数的对称轴，再结合开口方向得到函数的增减性；利用对称轴为直线和函数的增减性进行分析判断【详解】由表中数据可知，随的增大先增大后减小，函数图象开口向下，故C正确，不符合题意；时，或，函数的对称轴为直线，开口向下，当时，该函数有最大值1，故B正确，不符合题意；对称轴为直线，时，时，故A正确，不符合题意；在函数图象上有两点A，当、在对称轴右侧时，当在对称轴右侧、在对称轴左侧时，当在对称轴左侧、在对称轴左侧时，故D错误，符合题意；故选：D【
16、点睛】本题考查了二次函数的性质，解题的关键是掌握二次函数的性质12. 甲、乙两位同学放学后走路回家，他们走过的路程（千米）与所用的时间（分）之间的函数关系如图所示根据图中信息，下列说法正确的是（ ）A. 前10分钟，甲比乙的速度快B. 甲的平均速度为千米/分钟C. 经过30分钟，甲比乙走过的路程少D. 经过20分钟，甲、乙都走了千米【答案】D【解析】【分析】结合函数关系图逐项判断即可【详解】解：A项，前10分钟，甲走了千米，乙走了千米，则甲比乙的速度慢，故本选项不符合题意；B项，甲40分钟走了千米，则其平均速度为：千米/分钟，故本选项不符合题意；C项，经过30分钟，甲走了千米，乙走了千米，则甲
17、比乙多走了千米，故本选项不符合题意；D项，前20分钟，根据函数关系图可知，甲、乙都走了千米，故本选项符合题意；故选：D【点睛】本题考查了一次函数的图象及其在行程问题中的应用，理解函数关系图是解答本题的关键第卷(非选择题 共84分)注意事项：1第II卷分填空题和解答题；2第II卷所有题目的答案，考生须用0.5毫米黑色答字第答在答题卡规定的区域内，在试卷上答题不得分二、填空题(本大题共4个小题，每小题3分，共12分)13. 分解因式： _ 【答案】【解析】【分析】先提公因式，然后根据完全平方公式进行计算即可求解【详解】解：原式，故答案为：【点睛】本题考查了因式分解，掌握因式分解的方法是解题的关键1
18、4. 已知二元一次方程组，则的值为_【答案】2【解析】【分析】先将-得，即可求得答案【详解】原方程组为，由-得，故答案为：2【点睛】本题考查二元一次方程组的特殊解法，解题的关键是学会观察，并用整体法求解15. 如图，已知RtABC的边BC在x轴上，且A（1，2），B（-2，0）若将ABC平移，使点B落在点A处，则点C的对应点的坐标为_【答案】（4，2）【解析】【分析】根据A、B两点的坐标可得坐标的变化规律为横坐标加3，纵坐标加2，再把C点的坐标横坐标加3，纵坐标加2，即可求解【详解】解：将ABC平移，使点B落在点A处，点A（1，2），B（2，0），坐标的变化规律为横坐标加3，纵坐标加2，C（1
19、，0），点C的对应点的坐标为是（1+3，0+2），即（4，2）故答案为：（4，2）【点睛】本题考查了坐标系中的点、线段的平移规律，在平面直角坐标系中，图形的平移与图形上某点的平移相同平移过程中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减16. 如图，矩形中，相交于点O，过点B作交于点F，交与点M，过点D作交于点E，交于点N，连接，则下列结论：；当时，四边形是菱形其中，正确结论的个数是_【答案】4【解析】【分析】根据矩形的性质得到ABCD，ABCD，DAEBCF90，ODOBOAOC，ADBC，ADBC，根据平行线的性质得到DEAC，根据垂直的定义得到DNABMC90，由全等三角形
20、的性质得到DNBM，ADECBF，故正确；证ADECBF（ASA），得出AEFC，DEBF，故正确；证四边形NEMF是平行四边形，得出EMFN，故正确；证四边形DEBF是平行四边形，证出ODNABD，则DEBE，得出四边形DEBF是菱形；故正确；即可得出结论【详解】解：四边形ABCD是矩形，ABCD，ABCD，DAEBCF90，ODOBOAOC，ADBC，ADBC，DANBCM，BFAC，DEBF，DEAC，DNABMC90，在DNA和BMC中，DNABMC（AAS），DNBM，ADECBF，故正确；在ADE和CBF中，ADECBF（ASA），AEFC，DEBF，故正确；DEDNBFBM，即N
21、EMF，DEBF，四边形NEMF平行四边形，EMFN，故正确；ABCD，AECF，BEDF，BEDF，四边形DEBF是平行四边形，AOAD，AOADOD，AOD等边三角形，ADODAN60，ABD90ADO30，DEAC，ADNODN30，ODNABD，DEBE，四边形DEBF是菱形；故正确；故答案为：4【点睛】本题考查了矩形的性质、菱形的判定、平行四边形的判定与性质、全等三角形的判定与性质、等边三角形的判定与性质、等腰三角形的判定等知识；熟练掌握矩形的性质和菱形的判定，证明三角形全等是解题的关键三、解答题(本大题共7小题，共72分)17. 计算：（1）；（2）【答案】（1） （2）【解析】【
22、分析】（1）根据有理数的乘方，绝对值的化简，锐角三角函数的运算法则，即可求解；（2）根据分式的混合运算法则即可求解【小问1详解】【小问2详解】【点睛】本题考查有理数的乘方，绝对值的化简，锐角三角函数的运算法则，分式的混合运算法则，解题的关键是掌握运算法则，正确计算18. 某校为加强学生的安全意识，对七、八年级全体学生进行了安全知识测试，现要了解学生掌握安全知识的具体情况，从七、八年级各随机抽取50名学生进行数据分析，并对成绩(百分制)进行整理、描述和分析部分信息如下：A如图是所抽取的七年级成绩频数分布直方图B所抽取七年级成绩在这一组的是：70，72，74，75，76，76，77，77，77，7
23、8，79C七、八年级成绩的平均数、中位数如下：年级平均数中位数七76.9m八79.279.5根据以上信息，回答下列问题：（1）表中m的值为：_；（2）在这次测试中，七年级学生甲与八年级学生乙成绩都是79分，请判断两位学生在各自年级的排名谁更靠前，并说明理由；（3）该校七年级学生有500人，请估计七年级成绩超过平均分的人数【答案】（1） （2）甲的成绩在七年级的排名更靠前；理由见解析 （3）280人【解析】【分析】（1）利用中位数的定义求出七年级的中位数即可；（2）可以发现甲超过了七年级的中位数，乙没有超过八年级的中位数，由此即可得到答案；（3）用500乘以样本中超过平均成绩得人数占比即可得到答
24、案【小问1详解】解：将50名七年级学生的成绩从低到高排列，处在第25名和第26名的成绩分别为77，78，七年级的中位数为，故答案为：；【小问2详解】解：甲的成绩在七年级的排名更靠前，理由如下：七年级的中位数为，八年级的中位数为，甲的成绩超过七年级的中位数，乙的成绩没有超过八年级的中位数，甲的成绩在七年级的排名更靠前；【小问3详解】解：七年级参与调查的学生的平均成绩为，名，估计七年级成绩超过平均分的人数为280名【点睛】本题主要考查了简单的概率计算，求中位数，求平均数，用样本估计总体，频数分别直方图，灵活运用所学知识是解题的关键19. 越来越多太阳能路灯的使用，既点亮了城市的风景，也是我市积极落
25、实节能环保的举措，某校学生开展综合实践活动，测量太阳能路灯电池板离地面的高度，如图，已知测倾器的高度为1.5米，在测点A处安置测倾器，测得点M的仰角，在与点A相距3米的测点D处安置测倾器，测得点M的仰角(点A，D与N在一条直线上)求电池板离地面的高度的长(结果取整数，参考数据：，)【答案】7米【解析】【分析】过E作于F，连接，设米，可证四边形，四边形均是矩形，设，可求，由，解得 米，可求的长【详解】解：过E作于F，连接，则点B、E、F同一条直线上，设米，四边形，四边形均是矩形，米，米，,，解得 米，经检验米符合题意，米【点睛】本题考查矩形判定与性质，锐角三角函数，简单方程，掌握矩形判定与性质，
26、锐角三角函数，简单方程是解题关键20. 已知蓄电池的电压为定值，使用蓄电池时，电流I（A）与电阻R（）是反比例函数关系，当电阻R9时，电流I4A（1）求I关于R的函数表达式和自变量R的取值范围；（2）画出所求函数的图像；（3）若以此蓄电池为电源的用电器的限制电流不超过10A，求用电器可变电阻应控制在什么范围？【答案】（1）；（2）见解析；（3）用电器可变电阻应控制在不低于3.6欧的范围内【解析】【分析】（1）先由电流是电阻的反比例函数，可设，将，代入利用待定系数法即可求出这个反比例函数的解析式；（2）将的值分别代入（1）中所求的函数解析式，即可求出对应的值，从而完成图表，并描点画图；（3）将代
27、入（1）中所求的函数解析式即可确定电阻的取值范围【详解】解：（1）电流是电阻的反比例函数，设，时，解得，；（2）列表如下：34568910121297.264.543.63（3），即用电器可变电阻应控制在不低于3.6欧的范围内【点睛】本题考查了反比例函数的应用，解题的关键是正确地从中整理出函数模型，并利用函数的知识解决实际问题21. 如图，AB是O的直径，AC是O的切线，切点为A，BC交O于点D，点E是AC的中点（1）试判断直线DE与O的位置关系，并说明理由（2）若O半径为2，B60，求图中阴影部分的面积【答案】（1）直线DE与O相切，理由见解析（2）4-【解析】【分析】(1)连接0E、OD,
28、如图,根据切线的性质得OAC=90,再证明AOEDOE得到ODE=OAE=90,然后根据切线的判定定理得到DE为0的切线（2)先计算出四边形AEDO的面积,利用四边形的面积减去扇形的面积计算图中阴影部分的面积【详解】(1)直线DE与O相切理由如下：连接OE、OD,如图,AC是O的切线,.ABAC,OAC=90,点E是AC的中点,O点为AB的中点,OEBC.1=B,2=3OB=ODB=31=2,在AOE和DOE中 AOEDOE,ODE=OAE=90ODDEDE为O的切线;（2）S =ADOE=4=4S = S= S- S=4-【点睛】此题考查了切线的判定与性质,以及圆周角定理和扇形的面积公式,解
29、题关键在于利用切线性质证明三角形全等22. 科技创新是发展的第一动力某科研公司向市场推出了一款创新产品，该产品的成本价格是40元/件，销售价格y(元/件)与销售量x(件)之间满足一次函数关系，部分数据如下表：x（件）101520（元/件）585756（1）求y与x之间的函数关系式；（2）求销售利润w(元)关于销售量x(件)的函数解析式，当销售量为多少时，销售利润最大？最大值是多少？（3）为了保证销售利润不低于420元，求该产品的销售价格的取值范围【答案】（1） （2）当销售量为50件时，销售利润最大，最大值是500元 （3）【解析】【分析】（1）设，用待定系数法可得与之间的函数关系式为；（2）
30、根据题意，由二次函数的性质可得答案；（3）当时，解得或，结合（1）可得当销售利润不低于420元，该产品的销售价格的取值范围是【小问1详解】设，把，代入得：，解得，与之间的函数关系式为；【小问2详解】根据题意得：，当时，取最大值，最大值为500，当销售量为50件时，销售利润最大，最大值是500元；【小问3详解】当时，解得或，当时，；当时，；当销售利润不低于420元，该产品的销售价格的取值范围是【点睛】本题考查一次函数，二次函数的应用，解题的关键是读懂题意，列出函数关系式23. 正方形 ，点E为平面内一点，连接，将绕点B顺时针旋转得到 ，连接，已知点M为的中点，连接（1）如图1，若点E为边边上一点
31、，补全图形；判断并证明线段和的数量关系（2）如图2，若点E是的内部一点，（1）中线段和的数量关系是否仍然成立，如果成立，请证明；如果不成立，请说明理由【答案】（1）见解析，见解析 （2）成立，见解析【解析】【分析】（1）根据题意补全图形即可；用证明，可得，而，即知；（2）延长到N，使，连接，由，可得，即知，由绕点B顺时针旋转得到，有，得，故，即得，故，从而【小问1详解】补全图形，如图：四边形是正方形，将绕点B顺时针旋转90得到，F在上，M为斜辺的中点，；【小问2详解】（1）中线段和的数量关系仍然成立，证明如下：延长到N，使，连接，如图：M为的中点，绕点B顺时针旋转得到，；【点睛】本题考查了正方形的性质，旋转的性质，全等三角形的判断与性质，直角三角形斜边上的中线等知识，解题的关键是作辅助线，构造全等三角形
