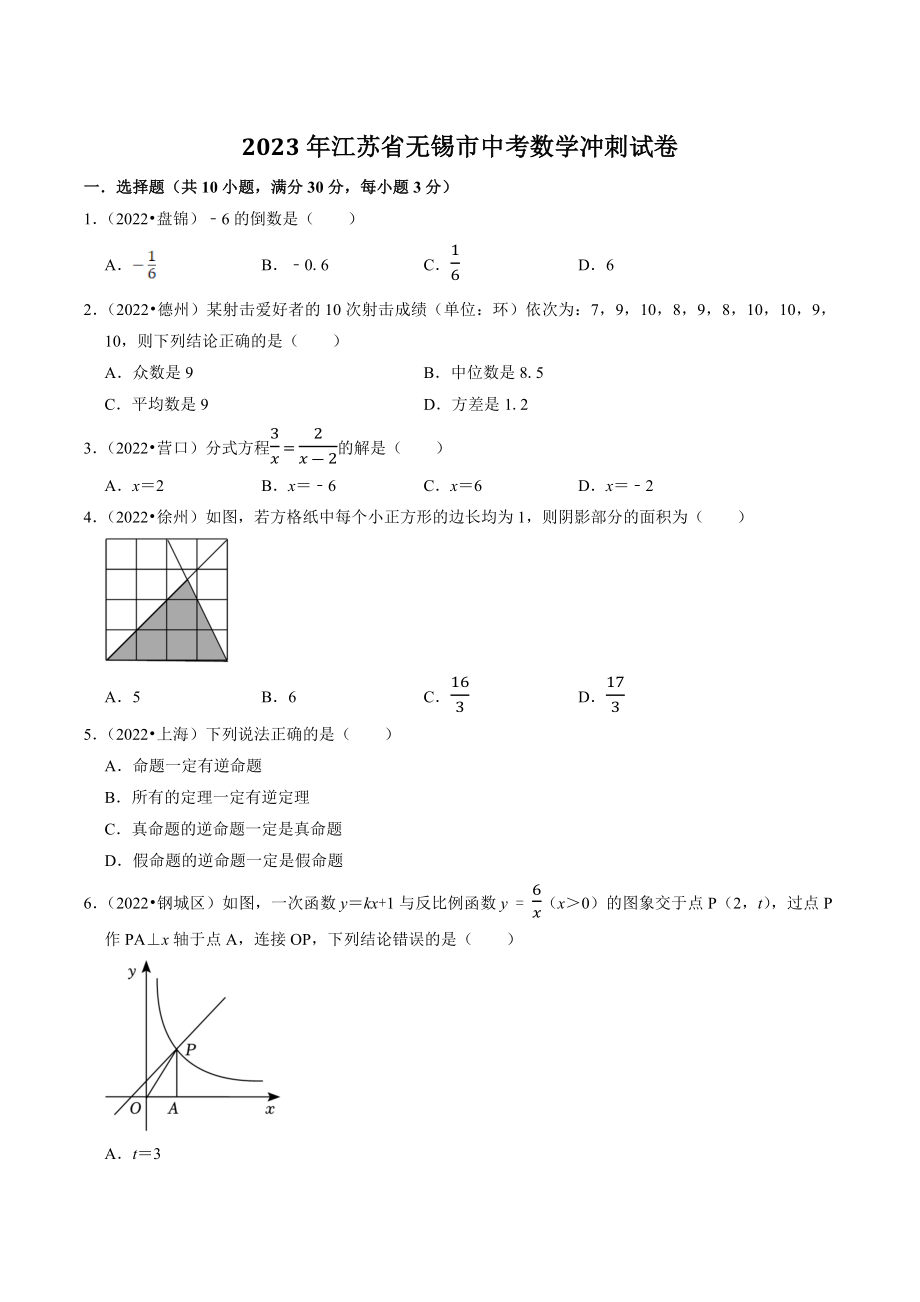
1、2023年江苏省无锡市中考数学冲刺试卷一选择题（共10小题，满分30分，每小题3分）1（2022盘锦）6的倒数是（）AB0.6C16D62（2022德州）某射击爱好者的10次射击成绩（单位：环）依次为：7，9，10，8，9，8，10，10，9，10，则下列结论正确的是（）A众数是9B中位数是8.5C平均数是9D方差是1.23（2022营口）分式方程3x=2x-2的解是（）Ax2Bx6Cx6Dx24（2022徐州）如图，若方格纸中每个小正方形的边长均为1，则阴影部分的面积为（）A5B6C163D1735（2022上海）下列说法正确的是（）A命题一定有逆命题B所有的定理一定有逆定理C真命题的逆命题
2、一定是真命题D假命题的逆命题一定是假命题6（2022钢城区）如图，一次函数ykx+1与反比例函数y=6x（x0）的图象交于点P（2，t），过点P作PAx轴于点A，连接OP，下列结论错误的是（）At3Bk1COAP 的面积是3D点B（m，n）在y=6x（x0）上，当m2时，nt7（2022济南）数学活动小组到某广场测量标志性建筑AB的高度如图，他们在地面上C点测得最高点A的仰角为22，再向前70m至D点，又测得最高点A的仰角为58，点C，D，B在同一直线上，则该建筑物AB的高度约为（）（精确到1m参考数据：sin220.37，tan220.40，sin580.85，tan581.60）A28mB
3、34mC37mD46m8（2022常州）在平面直角坐标系xOy中，点A与点A1关于x轴对称，点A与点A2关于y轴对称已知点A1（1，2），则点A2的坐标是（）A（2，1）B（2，1）C（1，2）D（1，2）9（2022镇江）如图，在等腰ABC中，BAC120，BC63，O同时与边BA的延长线、射线AC相切，O的半径为3将ABC绕点A按顺时针方向旋转（0360），B、C的对应点分别为B、C，在旋转的过程中边BC所在直线与O相切的次数为（）A1B2C3D410（2022朝阳）将一个三角尺按如图所示的方式放置在一张平行四边形的纸片上，EFG90，EGF60，AEF50，则EGC的度数为（）A100B
4、80C70D60二填空题（共8小题，满分24分，每小题3分）11（2022绵阳）因式分解：3x312xy2 12（2022东营）2022年2月20日，北京冬奥会圆满落幕，赛事获得了数十亿次数字平台互动，在中国仅电视收视人数就超6亿6亿用科学记数法表示为 13（2022沈阳）二元一次方程组x+2y=5y=2x的解是 14（2022济宁）已知直线y1x1与y2kx+b相交于点（2，1）请写出一个b值 （写出一个即可），使x2时，y1y215（2022黄石）如图，等边ABC中，AB10，点E为高AD上的一动点，以BE为边作等边BEF，连接DF，CF，则BCF ，FB+FD的最小值为 16（2022宿
5、迁）用半径为6cm，圆心角为120的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆的半径是 cm17（2022徐州）若一元二次方程x2+xc0没有实数根，则c的取值范围是 18（2022常州）如图，ABC是O的内接三角形若ABC45，AC=2，则O的半径是 三解答题（共10小题，满分96分）19（8分）（2022淮安）（1）计算：|5|+（3）02tan45；（2）化简：（1+3a-3）20（8分）（2022徐州）（1）解方程：x22x10；（2）解不等式组：21（10分）（2022内蒙古）一个不透明的口袋中装有四个完全相同的小球，上面分别标有数字1，2，3，4（1）从口袋中随机摸出一个小球，
6、求摸出小球上的数字是奇数的概率（直接写出结果）；（2）先从口袋中随机摸出一个小球，将小球上的数字记为x，在剩下的三个小球中再随机摸出一个小球，将小球上的数字记为y请用列表或画树状图法，求由x，y确定的点（x，y）在函数yx+4的图象上的概率22（10分）（2022西宁）如图，四边形ABCD是菱形，AEBC于点E，AFCD于点F（1）求证：ABEADF；（2）若AE4，CF2，求菱形的边长23（10分）（2022烟台）如图，O是ABC的外接圆，ABC45（1）请用尺规作出O的切线AD（保留作图痕迹，不写作法）；（2）在（1）的条件下，若AB与切线AD所夹的锐角为75，O的半径为2，求BC的长24
7、（10分）（2022绵阳）目前，全球淡水资源分布不均、总量不足是人类面临的共同问题某市在实施居民用水定额管理前，通过简单随机抽样对居民生活用水情况进行了调查，获得了若干个家庭去年的月均用水量数据（单位：t），整理出了频数分布表，频数分布直方图和扇形统计图，部分信息如下：月均用水量（t）2x3.53.5x55x6.56.5x88x9.5频数76对应的扇形区域ABCDE根据以上信息，解答下列问题：（1）补全频数分布直方图，并求出扇形图中扇形E对应的圆心角的度数；（2）为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按1.5倍价格收费，若要使该市60%的家庭水费支出不受影响，你觉得家庭月
8、均用水量应该定为多少？并说明理由25（10分）（2022宜昌）某造纸厂为节约木材，实现企业绿色低碳发展，通过技术改造升级，使再生纸项目的生产规模不断扩大该厂3，4月份共生产再生纸800吨，其中4月份再生纸产量是3月份的2倍少100吨（1）求4月份再生纸的产量；（2）若4月份每吨再生纸的利润为1000元，5月份再生纸产量比上月增加m%5月份每吨再生纸的利润比上月增加m2%，则5月份再生纸项目月利润达到66万元求m的值；（3）若4月份每吨再生纸的利润为1200元，4至6月每吨再生纸利润的月平均增长率与6月份再生纸产量比上月增长的百分数相同，6月份再生纸项目月利润比上月增加了25%求6月份每吨再生纸
9、的利润是多少元？26（10分）（2022资阳）小明学了解直角三角形内容后，对一条东西走向的隧道AB进行实地测量如图所示，他在地面上点C处测得隧道一端点A在他的北偏东15方向上，他沿西北方向前进1003米后到达点D，此时测得点A在他的东北方向上，端点B在他的北偏西60方向上，（点A、B、C、D在同一平面内）（1）求点D与点A的距离；（2）求隧道AB的长度（结果保留根号）27（10分）（2022无锡）如图1，矩形ABCD中，AB5，AD3，将ABC绕点A旋转到ABC位置，设AC交直线CD于点M（1）当点B恰好落在DC边上时，求ABC与矩形ABCD重叠部分的面积；（2）如图2，当点C、B、C恰好在一
10、直线上时，求DM的长度28（10分）（2022攀枝花）如图，二次函数yax2+bx+c的图象与x轴交于O（O为坐标原点），A两点，且二次函数的最小值为1，点M（1，m）是其对称轴上一点，y轴上一点B（0，1）（1）求二次函数的表达式；（2）二次函数在第四象限的图象上有一点P，连结PA，PB，设点P的横坐标为t，PAB的面积为S，求S与t的函数关系式；（3）在二次函数图象上是否存在点N，使得以A、B、M、N为顶点的四边形是平行四边形？若存在，直接写出所有符合条件的点N的坐标，若不存在，请说明理由2023年江苏省无锡市中考数学冲刺试卷一选择题（共10小题，满分30分，每小题3分）1（2022盘锦）
11、6的倒数是（）AB0.6C16D6【分析】根据乘积等于1的两个数互为倒数，从而确定6的倒数，注意：正数的倒数还是正数，负数的倒数还是负数【解答】解：6的倒数是1（6）故选：A【点评】本题考查了倒数的定义，熟练掌握倒数的定义是解题的关键2（2022德州）某射击爱好者的10次射击成绩（单位：环）依次为：7，9，10，8，9，8，10，10，9，10，则下列结论正确的是（）A众数是9B中位数是8.5C平均数是9D方差是1.2【分析】根据众数、中位数、平均数和方差的意义分别对每一项进行分析，即可得出答案【解答】解：A、10出现了4次，出现的次数最多，该组成绩的众数是10，故本选项不符合题意；B、该组成
12、绩的中位数是9+92=9，故本选项不符合题意；C、该组成绩x=110（7+9+10+8+9+8+10+10+9+10）9，故本选项符合题意；D、该组成绩数据的方差S2=110（79）2+2（89）2+3（99）2+4（109）21，故本选项不符合题意；故选：C【点评】此题考查了平均数、中位数、众数和方差的意义，解题的关键是正确理解各概念的含义3（2022营口）分式方程3x=2x-2的解是（）Ax2Bx6Cx6Dx2【分析】方程两边都乘x（x2）得出3（x2）2x，求出方程的解，再进行检验即可【解答】解：3x=2x-2，方程两边都乘x（x2），得3（x2）2x，解得：x6，检验：当x6时，x（x
13、2）0，所以x6是原方程的解，即原方程的解是x6，故选：C【点评】本题考查了解分式方程，能把分式方程转化成整式方程是解此题的关键4（2022徐州）如图，若方格纸中每个小正方形的边长均为1，则阴影部分的面积为（）A5B6C163D173【分析】证明ABECDE，求得AE：CE，再根据三角形的面积关系求得结果【解答】解：CDAB，ABECDE，AECE=ABCD=42=2，故选：C【点评】本题主要考查了相似三角形的性质与判定，三角形的面积公式，关键在于证明三角形相似5（2022上海）下列说法正确的是（）A命题一定有逆命题B所有的定理一定有逆定理C真命题的逆命题一定是真命题D假命题的逆命题一定是假命
14、题【分析】根据逆命题的概念、真假命题的概念判断即可【解答】解：A、命题一定有逆命题，本选项说法正确，符合题意，B、不是所有的定理一定有逆定理，例如全等三角形的对应角相等，没有逆定理，故本选项说法错误，不符合题意；C、真命题的逆命题不一定是真命题，故本选项说法错误，不符合题意；D、假命题的逆命题不一定是假命题，例如假命题对应角相等的三角形全等，其逆命题是真命题，故本选项说法错误，不符合题意；故选：A【点评】本题考查的是命题的真假判断、逆命题的概念，两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题其中一个命题称为另一个命题的逆命
15、题6（2022钢城区）如图，一次函数ykx+1与反比例函数y=6x（x0）的图象交于点P（2，t），过点P作PAx轴于点A，连接OP，下列结论错误的是（）At3Bk1COAP 的面积是3D点B（m，n）在y=6x（x0）上，当m2时，nt【分析】由反比例函数y=6x（x0）的图象交于点P（2，t），可得t3，判断A正确；把（2，3）代入ykx+1k1，判定B正确；由反比例函数中k的几何意义可判断C正确；根据y=6x的增减性可D错误【解答】解：反比例函数y=6x（x0）的图象交于点P（2，t），t3，故A正确，不符合题意；P（2，3），把（2，3）代入ykx+1得：2k+13，解得k1，故B正确
16、，不符合题意；PAx轴，y=6x，OAP 的面积是|6|2=3，故C正确，不符合题意；当x0时，y=6x中，y随x的增大而减小，m2时，n3，故D错误，符合题意，故选：D【点评】本题考查反比例函数，一次函数的交点问题，解题的关键是掌握函数图象上点坐标的特征，求出t和k的值7（2022济南）数学活动小组到某广场测量标志性建筑AB的高度如图，他们在地面上C点测得最高点A的仰角为22，再向前70m至D点，又测得最高点A的仰角为58，点C，D，B在同一直线上，则该建筑物AB的高度约为（）（精确到1m参考数据：sin220.37，tan220.40，sin580.85，tan581.60）A28mB34
17、mC37mD46m【分析】根据题意得到ABBC，然后根据三角函数的定义即可得到结论【解答】解：由题意可知：ABBC，在RtADB中，B90，ADB58，tanADBtan58=ABBD，BD（m），在RtACB中，B90，C22，CD70m，BCCD+BD（70+AB1.60）m，ABBCtanC（70+AB1.60）0.40（m），解得：AB37m，答：该建筑物AB的高度约为37m故选：C【点评】本题考查了解直角三角形的应用仰角俯角问题，解题的关键是借助仰角关系结合图形利用三角函数解直角三角形8（2022常州）在平面直角坐标系xOy中，点A与点A1关于x轴对称，点A与点A2关于y轴对称已知点
18、A1（1，2），则点A2的坐标是（）A（2，1）B（2，1）C（1，2）D（1，2）【分析】关于x轴的对称点的坐标特点：横坐标不变，纵坐标互为相反数关于y轴的对称点的坐标特点：横坐标互为相反数，纵坐标不变【解答】解：点A与点A1关于x轴对称，已知点A1（1，2），点A的坐标为（1，2），点A与点A2关于y轴对称，点A2的坐标为（1，2），故选：D【点评】此题主要考查了关于x轴、y轴对称的点的坐标规律，关键是熟练掌握点的变化规律，不要混淆9（2022镇江）如图，在等腰ABC中，BAC120，BC63，O同时与边BA的延长线、射线AC相切，O的半径为3将ABC绕点A按顺时针方向旋转（0360），B
19、、C的对应点分别为B、C，在旋转的过程中边BC所在直线与O相切的次数为（）A1B2C3D4【分析】设O与边BA的延长线、射线AC分别相切于点T、点G，连接OA交O于点L，连接OT，作AEBC于点E，OHBC于点H，先求得BECE33，BACB30，则AEBEtan303，再证明OABC，则OHAEOTOL3，可证明直线BC与O相切，再求得OA2OT6，则AL3，作AKBC于点K，由旋转得AKAE3，AKBAEB90，直线BC与O相切存在三种情况，一是ABC绕点A旋转到点K与点L重合，二是ABC绕点A旋转到BCOA，三是ABC绕点A旋转到BC与BC重合，即旋转角360，分别加以说明即可【解答】解
20、：如图1，由题意可知O同时与边BA的延长线、射线AC相切，O的半径为3，设O与边BA的延长线、射线AC分别相切于点T、点G，连接OA交O于点L，连接OT，ATOT，OT3，作AEBC于点E，OHBC于点H，则AEB90，ABAC，BAC120，BC63，BECE=12BC33，BACB=12（180BAC）30，AEBEtan3033，TAC180BAC60，OAGOAT=12TAC30，OAGACB，OABC，OHAEOTOL3，直线BC与O相切，ATO90，OA2OT6，AL3，作AKBC于点K，由旋转得AKAE3，AKBAEB90，如图2，ABC绕点A旋转到点K与点L重合，OLB180A
21、LB180AKB90，BCOL，OL为O的半径，BC与O相切；如图3，ABC绕点A旋转到BCOA，作ORBC交CB的延长线于点R，ORAK3，BC与O相切；当ABC绕点A旋转到BC与BC重合，即旋转角360，则BC与O相切，综上所述，在旋转的过程中边BC所在直线与O相切3次，故选：C【点评】此题重点考查等腰三角形的性质、圆的切线的判定、锐角三角函数以及数形结合与分类讨论数学思想的运用等知识与方法，画出图形并且正确地作出所需要的辅助线是解题的关键10（2022朝阳）将一个三角尺按如图所示的方式放置在一张平行四边形的纸片上，EFG90，EGF60，AEF50，则EGC的度数为（）A100B80C7
22、0D60【分析】由平行四边形的性质可得ABDC，再根据三角形内角和定理，即可得到GEF的度数，依据平行线的性质，即可得到EGC的度数【解答】解：四边形ABCD是平行四边形，ABDC，AEGEGC，EFG90，EGF60，GEF30，GEA80，EGC80故选：B【点评】此题考查的是平行四边形的性质，掌握其性质定理是解决此题的关键二填空题（共8小题，满分24分，每小题3分）11（2022绵阳）因式分解：3x312xy23x（x+2y）（x2y）【分析】先提取公因式，再套用平方差公式【解答】解：原式3x（x24y2）3x（x+2y）（x2y）故答案为：3x（x+2y）（x2y）【点评】本题考查了整
23、式的因式分解，掌握因式分解的提公因式法和公式法是解决本题的关键12（2022东营）2022年2月20日，北京冬奥会圆满落幕，赛事获得了数十亿次数字平台互动，在中国仅电视收视人数就超6亿6亿用科学记数法表示为 6108【分析】科学记数法的表示形式为a10n的形式，其中1|a|10，n为整数确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同当原数绝对值10时，n是正整数，当原数绝对值1时，n是负整数【解答】解：6亿6000000006108故答案为：6108【点评】此题考查科学记数法的表示方法科学记数法的表示形式为a10n的形式，其中1|a|10，n为整数，表示
24、时关键要正确确定a的值以及n的值13（2022沈阳）二元一次方程组x+2y=5y=2x的解是 x=1y=2【分析】用代入消元法解二元一次方程组即可【解答】解：，将代入，得x+4x5，解得x1，将x1代入，得y2，方程组的解为x=1y=2，故答案为：x=1y=2【点评】本题考查二元一次方程组，理解二元一次方程组的解，掌握二元一次方程组的解法是正确解答的关键14（2022济宁）已知直线y1x1与y2kx+b相交于点（2，1）请写出一个b值 0（答案不唯一）（写出一个即可），使x2时，y1y2【分析】由题意可知，当b1时满足题意，故b可以取0【解答】解：直线y1x1与y2kx+b相交于点（2，1）x
25、2时，y1y2b1，故b可以取0，故答案为：0（答案不唯一）【点评】本题考查了一次函数的性质，开放型题目，所写b的值必须满足b115（2022黄石）如图，等边ABC中，AB10，点E为高AD上的一动点，以BE为边作等边BEF，连接DF，CF，则BCF30，FB+FD的最小值为 53【分析】首先证明BAEBCF（SAS），推出BAEBCF30，作点D关于CF的对称点G，连接CG，DG，BG，BG交CF于点F，连接DF，此时BF+DF的值最小，最小值线段BG的长【解答】解：如图，ABC是等边三角形，ADCB，BAE=12BAC30，BEF是等边三角形，EBFABC60，BEBF，ABECBF，在B
26、AE和BCF中，BAEBCF（SAS），BAEBCF30，作点D关于CF的对称点G，连接CG，DG，BG，BG交CF的延长线于点F，连接DF，此时BF+DF的值最小，最小值线段BG的长DCFFCG30，DCG60，CDCG5，CDG是等边三角形，DBDCDG，CGB90，BG=BC2-CG2=102-52=53，BF+DF的最小值为53，故答案为：30，53【点评】本题考查旋转的性质，等边三角形的性质，轴对称最短问题等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型16（2022宿迁）用半径为6cm，圆心角为120的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆的半径是 2cm【
27、分析】设这个圆锥的底面圆的半径为rcm，利用扇形的弧长等于圆锥的底面圆的周长，列出方程，解方程即可得出答案【解答】解：设这个圆锥的底面圆的半径为rcm，由题意得：2r，解得：r2，这个圆锥的底面圆的半径为2cm，故答案为：2【点评】本题考查了圆锥的计算，理解扇形的弧长等于圆锥的底面圆的周长，从而列出方程是解决问题的关键17（2022徐州）若一元二次方程x2+xc0没有实数根，则c的取值范围是 c【分析】根据判别式的意义得到12+4c0，然后解不等式即可【解答】解：根据题意得12+4c0，解得c故答案为：c【点评】本题考查了一元二次方程ax2+bx+c0（a0）的根的判别式b24ac：当0，方程
28、有两个不相等的实数根；当0，方程有两个相等的实数根；当0，方程没有实数根18（2022常州）如图，ABC是O的内接三角形若ABC45，AC=2，则O的半径是 1【分析】连接AO并延长交O于点D，连接CD，根据直径所对的圆周角是直角可得ACD90，再利用同弧所对的圆周角相等可得ADC45，然后在RtACD中，利用锐角三角函数的定义求出AD的长，从而求出O的半径，即可解答【解答】解：连接AO并延长交O于点D，连接CD，AD是O的直径，ACD90，ABC45，ADCABC45，AD2，O的半径是1，故答案为：1【点评】本题考查了三角形的外接圆与外心，圆周角定理，根据题目的已知条件并结合图形添加适当的
29、辅助线是解题的关键三解答题（共10小题，满分96分）19（8分）（2022淮安）（1）计算：|5|+（3）02tan45；（2）化简：（1+3a-3）【分析】（1）先计算零次幂、代入特殊角的函数值，再化简绝对值，最后算加法；（2）先通分计算括号里面的，再把除法转化为乘法【解答】解：（1）原式5+1215+124；（2）原式 =1a+3【点评】本题考查了实数和分式的运算，掌握零次幂、绝对值的意义及分式的运算法则是解决本题的关键20（8分）（2022徐州）（1）解方程：x22x10；（2）解不等式组：【分析】（1）方程移项后，利用完全平方公式配方，开方即可求出解；（2）分别求出不等式组中两不等式的
30、解集，找出两解集的公共部分即可【解答】解：（1）方程移项得：x22x1，配方得：x22x+12，即（x1）22，开方得：x12，解得：x11+2，x21；（2），由得：x1，由得：x2，则不等式组的解集为x2【点评】此题考查了解一元一次不等式组，以及解一元二次方程配方法，熟练掌握不等式组的解法及方程的解法是解本题的关键21（10分）（2022内蒙古）一个不透明的口袋中装有四个完全相同的小球，上面分别标有数字1，2，3，4（1）从口袋中随机摸出一个小球，求摸出小球上的数字是奇数的概率（直接写出结果）；（2）先从口袋中随机摸出一个小球，将小球上的数字记为x，在剩下的三个小球中再随机摸出一个小球，将
31、小球上的数字记为y请用列表或画树状图法，求由x，y确定的点（x，y）在函数yx+4的图象上的概率【分析】（1）直接利用概率公式可得结果（2）画树状图得出所有等可能的结果数和由x，y确定的点（x，y）在函数yx+4的图象上的结果数，再利用概率公式可得出答案【解答】解：（1）口袋中共有4个小球，且小球上数字是奇数的有2个，摸出小球上的数字是奇数的概率为24=12（2）画树状图如下：共有12种等可能的结果，其中点在函数yx+4的图象上的有（1，3），（3，1），共2种，由x，y确定的点（x，y）在函数yx+4的图象上的概率为212=16【点评】本题考查列表法与树状图法、一次函数图象上点的坐标特征、概
32、率公式，熟练掌握列表法与树状图法以及概率公式是解答本题的关键用到的知识点为：概率22（10分）（2022西宁）如图，四边形ABCD是菱形，AEBC于点E，AFCD于点F（1）求证：ABEADF；（2）若AE4，CF2，求菱形的边长【分析】（1）由菱形ABCD的四条边相等、对角相等的性质知ABAD，BD；然后根据已知条件“AEBC，AFCD”知AEBAFD；最后由全等三角形的判定定理AAS证明ABEADF；（2）由全等三角形ABEADF的对应边相等知BEDF，然后根据菱形的四条边相等求得ABCD，设ABCDx，已知CF2，则BEDFx2，利用勾股定理即可求出菱形的边长【解答】（1）证明：四边形A
33、BCD是菱形，ABBCCDAD，BD，AEBC，AFCD，AEBAFD，在ABE和ADF中，ABEADF（AAS）；（2）解：设菱形的边长为x，ABCDx，CF2，DFx2，ABEADF，BEDFx2，在RtABE中，根据勾股定理得，AE2+BE2AB2，即42+（x2）2x2，解得x5，菱形的边长是5【点评】本题考查了菱形的性质，解题的关键熟记菱形的性质并灵活运用菱形的性质菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线23（10分）（2022烟台）如图，O是ABC的外接圆，A
34、BC45（1）请用尺规作出O的切线AD（保留作图痕迹，不写作法）；（2）在（1）的条件下，若AB与切线AD所夹的锐角为75，O的半径为2，求BC的长【分析】（1）过点A作ADAO即可；（2）连接OB，OC证明ACB75，利用三角形内角和定理求出CAB，推出BOC120，求出CH可得结论【解答】解：（1）如图，切线AD即为所求；（2）过点O作OHBC于H，连接OB，OCAD是切线，OAAD，OAD90，DAB75，OAB15，OAOB，OABOBA15，BOA150，BCA=12AOB75，ABC45，BAC180457560，BOC2BAC120，OBOC2，BCOCBO30，OHBC，CHB
35、HOCcos30=3，BC23【点评】本题考查作图复杂作图，三角形的外接圆，切线的判定和性质，解直角三角形等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型24（10分）（2022绵阳）目前，全球淡水资源分布不均、总量不足是人类面临的共同问题某市在实施居民用水定额管理前，通过简单随机抽样对居民生活用水情况进行了调查，获得了若干个家庭去年的月均用水量数据（单位：t），整理出了频数分布表，频数分布直方图和扇形统计图，部分信息如下：月均用水量（t）2x3.53.5x55x6.56.5x88x9.5频数76对应的扇形区域ABCDE根据以上信息，解答下列问题：（1）补全频数分布直方图，并求出
36、扇形图中扇形E对应的圆心角的度数；（2）为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按1.5倍价格收费，若要使该市60%的家庭水费支出不受影响，你觉得家庭月均用水量应该定为多少？并说明理由【分析】（1）根据题A的频数和百分比得到抽取的总数，进而求得B、C的频数即可补全频数分布直方图，求出E的频数，360乘以E所占的比例即可求解；（2）由于5060%30，所以为了鼓励节约用水，要使60%的家庭收费不受影响，即要使30户的家庭收费不受影响，而7+2330，故家庭月均用水量应该定为5吨【解答】解：（1）抽取的总数为：714%50，B的频数为：5046%23，C的频数为：5024%12
37、，频数分布直方图如下：扇形图中扇形E对应的圆心角的度数为：36014.4；（2）要使60%的家庭收费不受影响，家庭月均用水量应该定为5吨，理由如下：因为月平均用水量不超过5吨的有7+2330（户），305060%【点评】本题考查读频数分布直方图和频数分布表的能力及利用统计图表获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题25（10分）（2022宜昌）某造纸厂为节约木材，实现企业绿色低碳发展，通过技术改造升级，使再生纸项目的生产规模不断扩大该厂3，4月份共生产再生纸800吨，其中4月份再生纸产量是3月份的2倍少100吨（1）求4月份再生纸的产量
38、；（2）若4月份每吨再生纸的利润为1000元，5月份再生纸产量比上月增加m%5月份每吨再生纸的利润比上月增加m2%，则5月份再生纸项目月利润达到66万元求m的值；（3）若4月份每吨再生纸的利润为1200元，4至6月每吨再生纸利润的月平均增长率与6月份再生纸产量比上月增长的百分数相同，6月份再生纸项目月利润比上月增加了25%求6月份每吨再生纸的利润是多少元？【分析】（1）设3月份再生纸的产量为x吨，则4月份再生纸的产量为（2x100）吨，根据该厂3，4月份共生产再生纸800吨，即可得出关于x的一元一次方程，解之即可求出x的值，再将其代入（2x100）中即可求出4月份再生纸的产量；（2）利用月利润
39、每吨的利润月产量，即可得出关于m的一元二次方程，解之取其正值即可得出结论；（3）设4至6月每吨再生纸利润的月平均增长率为y，5月份再生纸的产量为a吨，根据6月份再生纸项目月利润比上月增加了25%，即可得出关于y的一元二次方程，化简后即可得出6月份每吨再生纸的利润【解答】解：（1）设3月份再生纸的产量为x吨，则4月份再生纸的产量为（2x100）吨，依题意得：x+2x100800，解得：x300，2x1002300100500答：4月份再生纸的产量为500吨（2）依题意得：1000（1+m2%）500（1+m%）660000，整理得：m2+300m64000，解得：m120，m2320（不合题意，
40、舍去）答：m的值为20（3）设4至6月每吨再生纸利润的月平均增长率为y，5月份再生纸的产量为a吨，依题意得：1200（1+y）2a（1+y）（1+25%）1200（1+y）a，1200（1+y）21500答：6月份每吨再生纸的利润是1500元【点评】本题考查了一元一次方程的应用以及一元二次方程的应用，找准等量关系，正确列出一元一次方程（或一元二次方程）是解题的关键26（10分）（2022资阳）小明学了解直角三角形内容后，对一条东西走向的隧道AB进行实地测量如图所示，他在地面上点C处测得隧道一端点A在他的北偏东15方向上，他沿西北方向前进1003米后到达点D，此时测得点A在他的东北方向上，端点B
41、在他的北偏西60方向上，（点A、B、C、D在同一平面内）（1）求点D与点A的距离；（2）求隧道AB的长度（结果保留根号）【分析】（1）根据方位角图，易知ACD60，ADC90，解RtADC即可求解；（2）过点D作DEAB于点E分别解RtADE，RtBDE求出AE和BE，即可求出隧道AB的长【解答】解；（1）由题意可知：ACD15+4560，ADC180454590，在RtADC中，（米），答：点D与点A的距离为300米（2）过点D作DEAB于点E，AB是东西走向，ADE45，BDE60，在RtADE中，（米），在RtBDE中，（米），AB=AE+BE=(1502+1506)（米），答：隧道AB的长为(1502+1506)米【点评】本题考查了解直角三角形的应用方向角问题，掌握方向角的概念，掌握特殊角的三角函数值是解题的关键27（10分）（2022无锡）如图1，矩形ABCD中，AB5，AD3，将ABC绕
