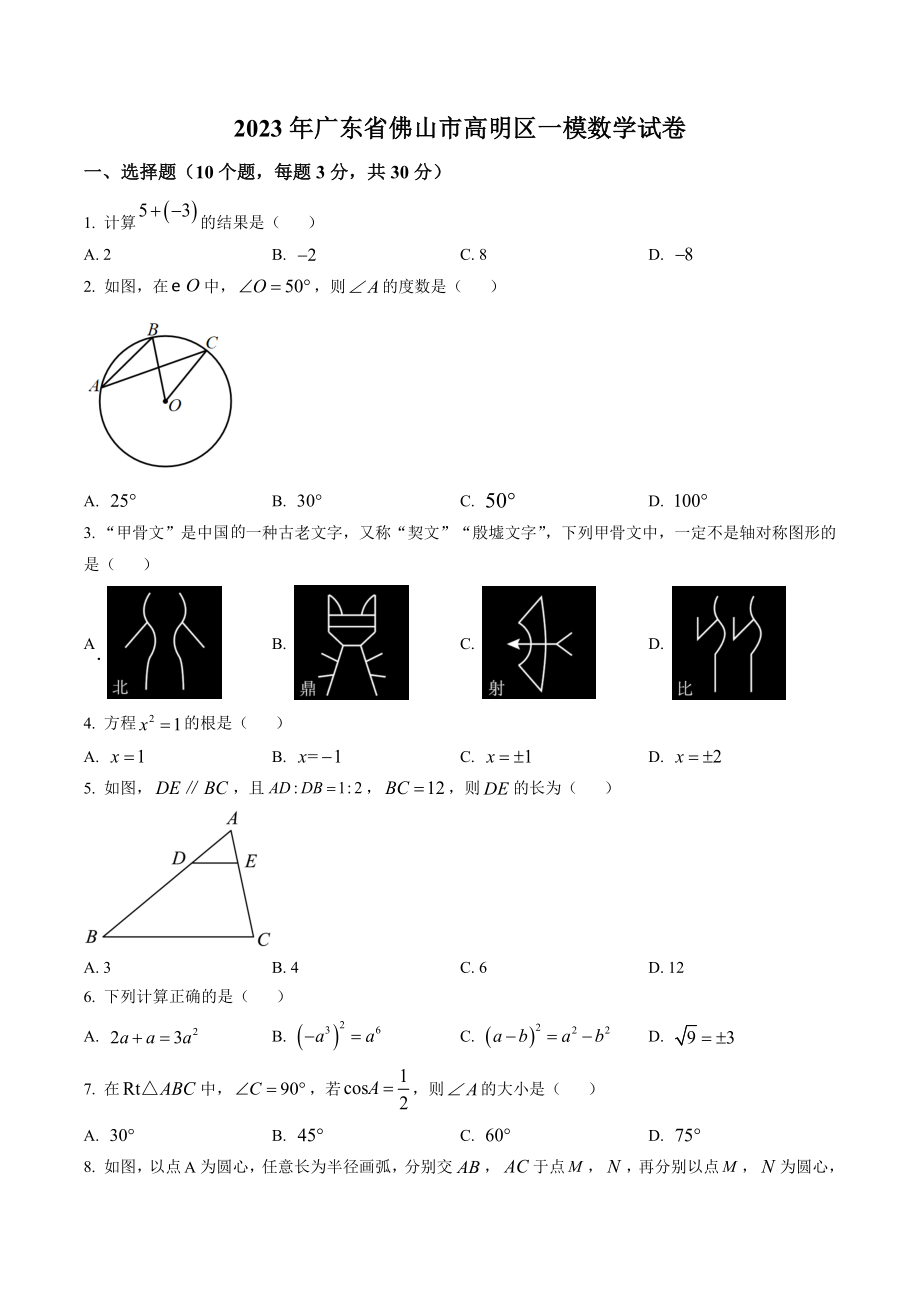
1、2023年广东省佛山市高明区一模数学试卷一、选择题（10个题，每题3分，共30分）1. 计算的结果是（ ）A. 2B. C. 8D. 2. 如图，在中，则的度数是（ ）A. B. C. D. 3. “甲骨文”是中国一种古老文字，又称“契文”“殷墟文字”，下列甲骨文中，一定不是轴对称图形的是（ ）A B. C. D. 4. 方程的根是（ ）A. B. C. D. 5. 如图，且，则的长为（ ）A. 3B. 4C. 6D. 126. 下列计算正确的是（ ）A. B. C. D. 7. 在中，若，则的大小是（ ）A. B. C. D. 8. 如图，以点为圆心，任意长为半径画弧，分别交，于点，再分别以
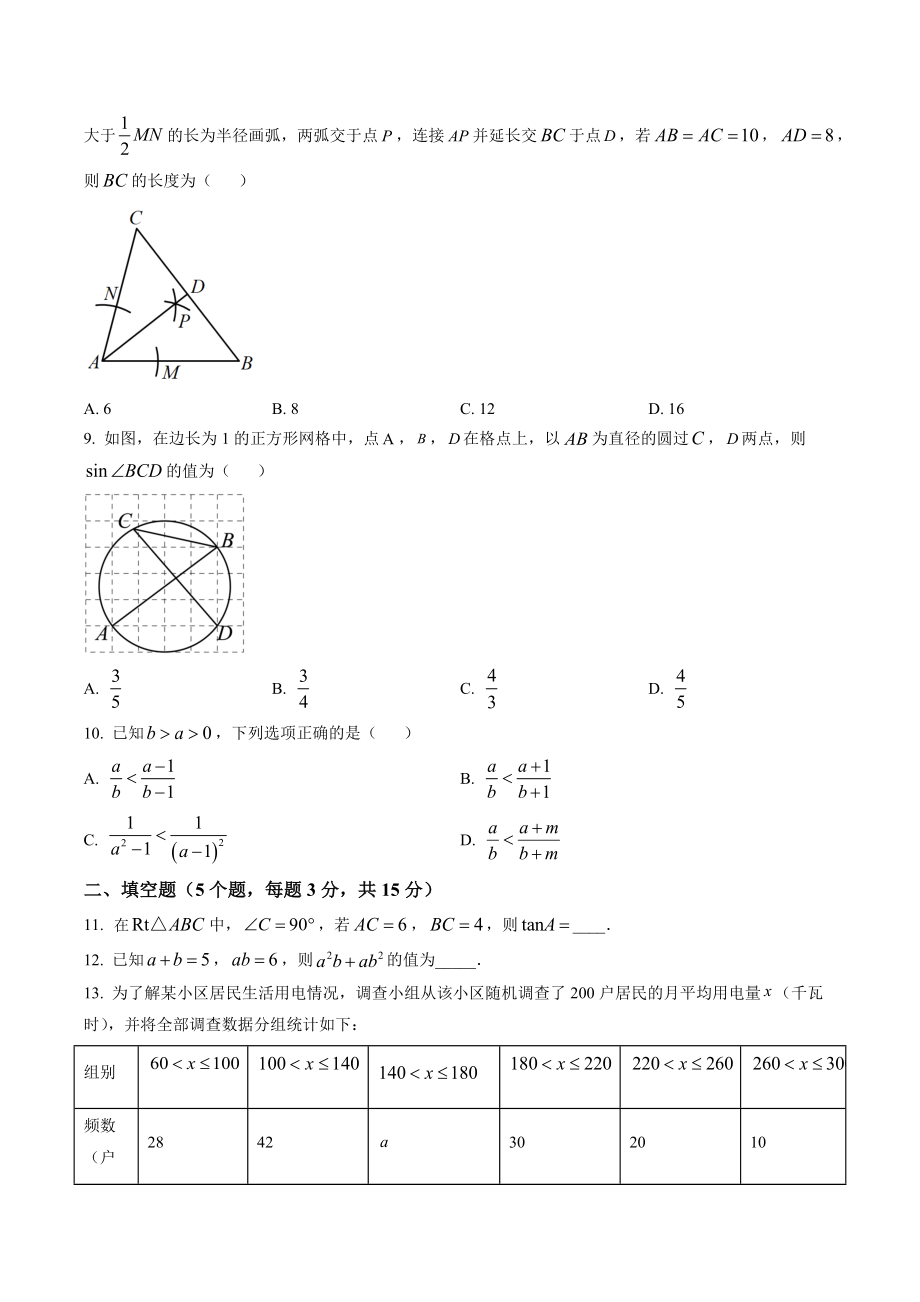
2、点，为圆心，大于的长为半径画弧，两弧交于点，连接并延长交于点，若，则的长度为（ ）A. 6B. 8C. 12D. 169. 如图，在边长为1的正方形网格中，点，在格点上，以为直径的圆过，两点，则的值为（ ）A. B. C. D. 10. 已知，下列选项正确的是（ ）A. B. C. D. 二、填空题（5个题，每题3分，共15分）11. 中，若，则_12. 已知，则的值为_13. 为了解某小区居民生活用电情况，调查小组从该小区随机调查了200户居民的月平均用电量（千瓦时），并将全部调查数据分组统计如下：组别频数（户数）2842302010把这200个数据从小到大排列后，其中第98到第102个数据
3、依次为：150，152，152，154，160，这200户居民月平均用电量的中位数为_14. 如图，二次函数（）图象的对称轴为直线，与轴的一个交点坐标为，给出下列结论：；图象与轴的另一个交点为；当时，随的增大而增大，正确结论的序号是_15. 如图，某同学画的反比例函数的图象如图所示，请写出图象中的错误_三、解答题（8个题，共75分）16. 计算：17. 解方程：18. 九章算术标志中国古代数学形成了完整的体系，第九卷勾股中记载了一个“圆材埋壁”的问题：“今有圆材埋在壁中，不知大小.以锯锯之，深一寸，锯道长一尺，问径几何？”用现在的数学语言可表述为：“如图，是的直径，弦于点，寸，寸，求直径的长，
4、”请你解答这个问题19. 点与点在同一平面直角坐标系中（1）若点位于第四象限，求的取值范围；（2）若点与点关于轴对称，求线段的长度20. 如图，海中小岛周围内有暗礁渔船跟踪鱼群由西向东航行，在点处测得小岛在北偏东方向上；航行到达点，这时测得小岛在北偏东方向上如果渔船不改变航线继续向东航行，有没有触礁的危险？（参考数据：，）21. 已知二次函数图象的顶点坐标是，且经过点（1）求二次函数的表达式，并画出图象；（2）二次函数的图象与一次函数的图象相交吗？若相交，求出它们的交点坐标：（3）若二次函数图象经过平移后过原点，可以怎样平移？22. 如图，经过正方形的顶点，与相切于点，分别交，于点，连接（1）
5、求证：四边形是矩形；（2）求值23. 二次函数（1）当时，函数图象与轴交于点、，与轴交于点写出函数的一个性质；如图1，点是第四象限内函数图象上一动点，求出点坐标，使得的面积最大；如图2，点为第一象限内函数图象上一动点，过点作.轴，垂足为，的外接圆与交于点，求的长度；（2）点、为函数图象上任意两点，且.若对于时，都有，求的取值范围一、选择题（10个题，每题3分，共30分）1. 计算的结果是（ ）A. 2B. C. 8D. 【答案】A【解析】【分析】根据有理数的加法法则求解即可【详解】解：，故选：A【点睛】本题考查有理数的加法，属于基础题，掌握加法法则是关键2. 如图，在中，则的度数是（ ）A.
6、B. C. D. 【答案】A【解析】【分析】直接利用“在同圆或等圆中，一条弧所对的圆周角是它所对的圆心角的一半”解题即可【详解】解：在中，故选A【点睛】本题考查圆周角定理，掌握同弧所对的圆周角是圆心角的一半是解题的关键3. “甲骨文”是中国的一种古老文字，又称“契文”“殷墟文字”，下列甲骨文中，一定不是轴对称图形的是（ ）A. B. C. D. 【答案】D【解析】【分析】根据如果一个图形沿一条直线折叠，直线两旁部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可【详解】解：A，B，C选项中的图形都能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以都
7、是轴对称图形；D选项中的图形不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；故选：D【点睛】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合4. 方程的根是（ ）A. B. C. D. 【答案】C【解析】【分析】利用平方根的定义求解即可【详解】解：，故选：C【点睛】本题考查平方根，解答的关键是熟知一个正数的平方根有两个且互为相反数5. 如图，且，则的长为（ ）A. 3B. 4C. 6D. 12【答案】B【解析】【分析】利用平行线的性质可得，可证，利用相似三角形对应边成比例可得，结合已知条件即可求解【详解】解：，解得，
8、故选B【点睛】本题主要考查相似三角形的判定与性质，证明是解题的关键6. 下列计算正确的是（ ）A. B. C. D. 【答案】B【解析】【分析】根据合并同类项法则、幂的乘方法则、平方差公式、算术平方根的定义逐项判断即可【详解】解：A，故该选项计算错误，不合题意；B，故该选项计算正确，符合题意；C，故该选项计算错误，不合题意；D，故该选项计算错误，不合题意；故选B【点睛】本题考查合并同类项、幂的乘方、平方差公式、算术平方根等知识点，属于基础题，熟练掌握运算法则并正确计算是解题的关键7. 在中，若，则的大小是（ ）A. B. C. D. 【答案】C【解析】【分析】根据特殊角的三角函数值求解即可【详
9、解】解：，是的内角，又，故选：C【点睛】本题考查特殊角的三角函数值，熟记特殊角的三角函数值是解答的关键8. 如图，以点为圆心，任意长为半径画弧，分别交，于点，再分别以点，为圆心，大于的长为半径画弧，两弧交于点，连接并延长交于点，若，则的长度为（ ）A. 6B. 8C. 12D. 16【答案】C【解析】【分析】先根据作图痕迹得到平分，再根据等腰三角形的三线合一证得，再根据勾股定理求得即可【详解】解：由作图痕迹得到平分，在中，故选：C【点睛】本题考查了基本尺规作图-作角平分线、等腰三角形的性质、勾股定理，熟悉基本作图，掌握等腰三角形的三线合一性质是解答的关键9. 如图，在边长为1的正方形网格中，点
10、，在格点上，以为直径的圆过，两点，则的值为（ ）A. B. C. D. 【答案】A【解析】【分析】根据同弧所对的圆周角相等可得，根据直径所对的圆周角为90度可得，因此解求出即可【详解】解：连接、，都是所对的圆周角，为直径，由图可知，故选A【点睛】本题考查圆周角定理，勾股定理，锐角三角函数等，利用同弧所对的圆周角相等得出是解题的关键10. 已知，下列选项正确的是（ ）A. B. C. D. 【答案】B【解析】【分析】根据作差法和不等式的性质逐项求解判断即可【详解】解：A、，当即时，则，故A选项计算错误，不符合题意；B、，则，故B选项正确，符合题意；C、当时，和无意义，故C选项错误，不符合题意；D
11、、当时，同选项A不一定成立，故选项D错误，不符合题意，故选：B【点睛】本题考查不等式的性质、分式的加减运算，解答的关键是利用作差法比较式子的大小关系二、填空题（5个题，每题3分，共15分）11. 在中，若，则_【答案】【解析】【分析】根据三角函数的定义得出即可【详解】解：，若，故答案为：【点睛】本题主要考查锐角三角函数的定义，解题的关键是熟记三角函数的定义12. 已知，则的值为_【答案】30【解析】【分析】先对进行提公因式，在代入求值即可【详解】解：故答案为：30【点睛】此题考查了因式分解，解题的关键是正确进行因式分解并计算13. 为了解某小区居民生活用电情况，调查小组从该小区随机调查了200
12、户居民的月平均用电量（千瓦时），并将全部调查数据分组统计如下：组别频数（户数）2842302010把这200个数据从小到大排列后，其中第98到第102个数据依次为：150，152，152，154，160，这200户居民月平均用电量的中位数为_【答案】153【解析】【分析】根据中位数的定义求解【详解】解：在所给200个数据中，按从小到大的顺序排列后，第100个和第101个数据为152和154，这200户居民月平均用电量的中位数为，故答案为：153【点睛】本题考查中位数的定义，中位数是一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数），注意先进行排序14. 如图，二
13、次函数（）图象的对称轴为直线，与轴的一个交点坐标为，给出下列结论：；图象与轴的另一个交点为；当时，随的增大而增大，正确结论的序号是_【答案】【解析】【分析】根据二次函数的图象与性质逐个判断即可【详解】解：抛物线的开口向下，与y轴的正半轴相交，故正确；抛物线的对称轴为直线，与轴的一个交点坐标为，与轴一个交点坐标为，故正确；由图象可知，当时，随增大而增大，故正确，综上，正确结论的序号是，故答案为：【点睛】本题考查二次函数的图象与性质、二次函数图象与x轴的交点问题，熟练掌握抛物线的位置与系数间的关系是正确判断的关键15. 如图，某同学画反比例函数的图象如图所示，请写出图象中的错误_【答案】图象形状错
14、误；不满足函数定义；与y轴有交点；对应点的位置不正确等【解析】【分析】根据反比例函数的图象与性质进行观察判断【详解】解：观察图象，主要错误有：图象形状错误：反比例函数的图象是两支双曲线，不是射线组成；不满足函数定义：有一个x值，对应两个y值；与y轴有交点：中，图象不可能与坐标轴相交；对应点的位置不正确：比如，当时，即图象需经过点，故答案为：图象形状错误；不满足函数定义；与y轴有交点；图象上对应点的位置不正确等【点睛】本题考查反比例函数的图象，熟知反比例函数的图象特征以及与坐标轴的关系是解答的关键三、解答题（8个题，共75分）16. 计算：【答案】0【解析】【分析】先利用二次根式的性质和特殊角的
15、三角函数值化简各数，再加减运算即可求解【详解】解：【点睛】本题考查含特殊角的三角函数值的混合运算、二次根式的加减运算，熟记特殊角 的三角函数值并正确求解是解答的关键17. 解方程：【答案】无解【解析】【分析】根据解分式方程的解法步骤求解即可【详解】解：去分母，得，移项，合并同类项，得，检验：当时，是原方程的增根，即原方程无解【点睛】本题考查解分式方程，熟练掌握解分式方程的解法步骤，注意计算结果要检验18. 九章算术标志中国古代数学形成了完整的体系，第九卷勾股中记载了一个“圆材埋壁”的问题：“今有圆材埋在壁中，不知大小.以锯锯之，深一寸，锯道长一尺，问径几何？”用现在的数学语言可表述为：“如图，
16、是的直径，弦于点，寸，寸，求直径的长，”请你解答这个问题【答案】直径的长为寸【解析】【分析】连接，设的半径为r，利用垂径定理得到寸，再利用勾股定理求解即可【详解】接：连接，设的半径为r，是的直径，在中，根据勾股定理得，解得，即直径的长为寸【点睛】本题考查了垂径定理、勾股定理，熟练掌握垂径定理是解答的关键19. 点与点在同一平面直角坐标系中（1）若点位于第四象限，求的取值范围；（2）若点与点关于轴对称，求线段的长度【答案】（1） （2）【解析】【分析】（1）根据位于第四象限得到，解不等式组即可得到答案；（2）由点与点关于轴对称得到，得到，综上可知，得到点，即可得到答案【小问1详解】解：位于第四象
17、限，解得，即的取值范围是；【小问2详解】点与点关于轴对称，由解得，由得，解得，综上可知，此时，点，线段的长度为【点睛】此题考查了点所在的象限、关于y轴对称的点，用到了解不等式（组）和解一元二次方程，理解题意并准确计算是解题的关键20. 如图，海中小岛周围内有暗礁渔船跟踪鱼群由西向东航行，在点处测得小岛在北偏东方向上；航行到达点，这时测得小岛在北偏东方向上如果渔船不改变航线继续向东航行，有没有触礁的危险？（参考数据：，）【答案】渔船不改变航线继续向东航行，没有触礁的危险【解析】【分析】过A作交延长线于E，根据题意得到，利用正切定义用分别表示出，利用列方程求解即可【详解】解：过A作交延长线于E，由
18、题意，得，在中，在中，则，解得，渔船不改变航线继续向东航行，没有触礁的危险【点睛】本题考查解直角三角形的应用，解决的关键是作高线构造直角三角形解决问题21. 已知二次函数图象的顶点坐标是，且经过点（1）求二次函数的表达式，并画出图象；（2）二次函数的图象与一次函数的图象相交吗？若相交，求出它们的交点坐标：（3）若二次函数图象经过平移后过原点，可以怎样平移？【答案】（1）或，图象见解析 （2）相交，交点坐标为和 （3）可将二次函数的图象向左平移1个单位长度或者向右平移2个单位长度得到的二次函数的图象经过原点【解析】【分析】（1）利用顶点式设所求的二次函数表达式，再代入求解即可得到函数表达式；利用
19、描点法画出图象即可；（2）两个函数联立方程组，判断方程的解的情况即可得出结论；（3）利用二次函数与x轴的交点坐标和平移性质即可得到平移方案【小问1详解】解：根据题意，设二次函数的表达式为，将代入，得，解得，此二次函数的表达式为，即；当时，则抛物线与y轴交于，又抛物线的对称轴为直线，抛物线还经过点；当时，由得，则抛物线与x轴交于和，画出该二次函数图象如图：【小问2详解】解：由得，方程有两个不相等的实数根，二次函数的图象与一次函数的图象相交；解方程得：，当时，；当时，所以交点坐标为和；【小问3详解】解：抛物线与x轴交于和，可将二次函数的图象向左平移1个单位长度或者向右平移2个单位长度得到的二次函数
20、的图象经过原点【点睛】本题考查待定系数法求二次函数的表达式、用描点法画二次函数的图象、二次函数与一元二次方程的关系、根的判别式、二次函数图象的平移等知识，熟练掌握相关知识的联系与运用时解答的关键22. 如图，经过正方形的顶点，与相切于点，分别交，于点，连接（1）求证：四边形是矩形；（2）求的值【答案】（1）见解析 （2）【解析】【分析】（1）根据正方形的性质、圆内接四边形的的性质证得即可证得结论；（2）连接并延长交于N，过O作于M，先根据切线性质和垂径定理证得 ，设，则，再证明四边形和四边形都是矩形得到，连接，根据勾股定理得求得，进而可求解【小问1详解】证明：四边形是正方形，四边形是的内接四边
21、形，四边形是矩形；【小问2详解】解：连接并延长交于N，过O作于M，则，四边形是正方形，与相切于点，则，设，则，四边形和四边形都是矩形，连接，则，在中， 根据勾股定理得，则，解得或（舍去），【点睛】本题考查了正方形的性质、矩形的判定与性质、切线性质、垂径定理、勾股定理、圆内接四边形的性质等知识，熟练掌握相关知识的联系与运用，利用切线性质和垂径定理以及矩形的性质求解是解答的关键23. 二次函数（1）当时，函数图象与轴交于点、，与轴交于点写出函数的一个性质；如图1，点是第四象限内函数图象上一动点，求出点坐标，使得的面积最大；如图2，点为第一象限内函数图象上一动点，过点作.轴，垂足为，的外接圆与交于点
22、，求的长度；（2）点、为函数图象上任意两点，且.若对于时，都有，求的取值范围【答案】（1）函数图象的顶点坐标为； （2）【解析】【分析】（1）先求得二次函数的解析式，根据解析式和二次函数的性质写出性质即可；根据二次函数的解析式求得点A、B、C的坐标，再求得直线的解析式，过点P作轴于H，设，则，进而，利用二次函数的性质求解即可；设圆心为H，过H作轴于N，于M，连接，利用垂径定理可得，设，利用坐标与图形性质得到，证明四边形是矩形得到，然后利用勾股定理得到，进而求得x值即可求解；（2）根据二次函数的性质得到该二次函数图象开口向上，对称轴为直线，则当时，y随x的增大而增大，进而根据点M、N的中点坐标和
23、对称轴的位置关系即可求解【小问1详解】解：当时，函数图象的顶点坐标为；令，由得，当时，设直线的解析式为，将代入，得，解得，直线的解析式为，过点P作轴于H， 与交于G，设，则，当时，有最大值，最大值为；设圆心为H，过H作轴于N，于M，连接，则，设，轴，四边形是矩形，在中，在中，则，解得，即；【小问2详解】解：由于二次函数图象开口向上，对称轴为直线，当时，y随x的增大而增大，点、为函数图象上任意两点，且，若对于即时，都有，【点睛】本题是二次函数的综合题，涉及待定系数法求函数解析式、坐标与图形、二次函数的图象与性质、三角形的面积、矩形的判定与性质、垂径定理、勾股定理等知识，熟练掌握二次函数的图象与性质，利用数形结合思想进行分析求解是解答的关键
