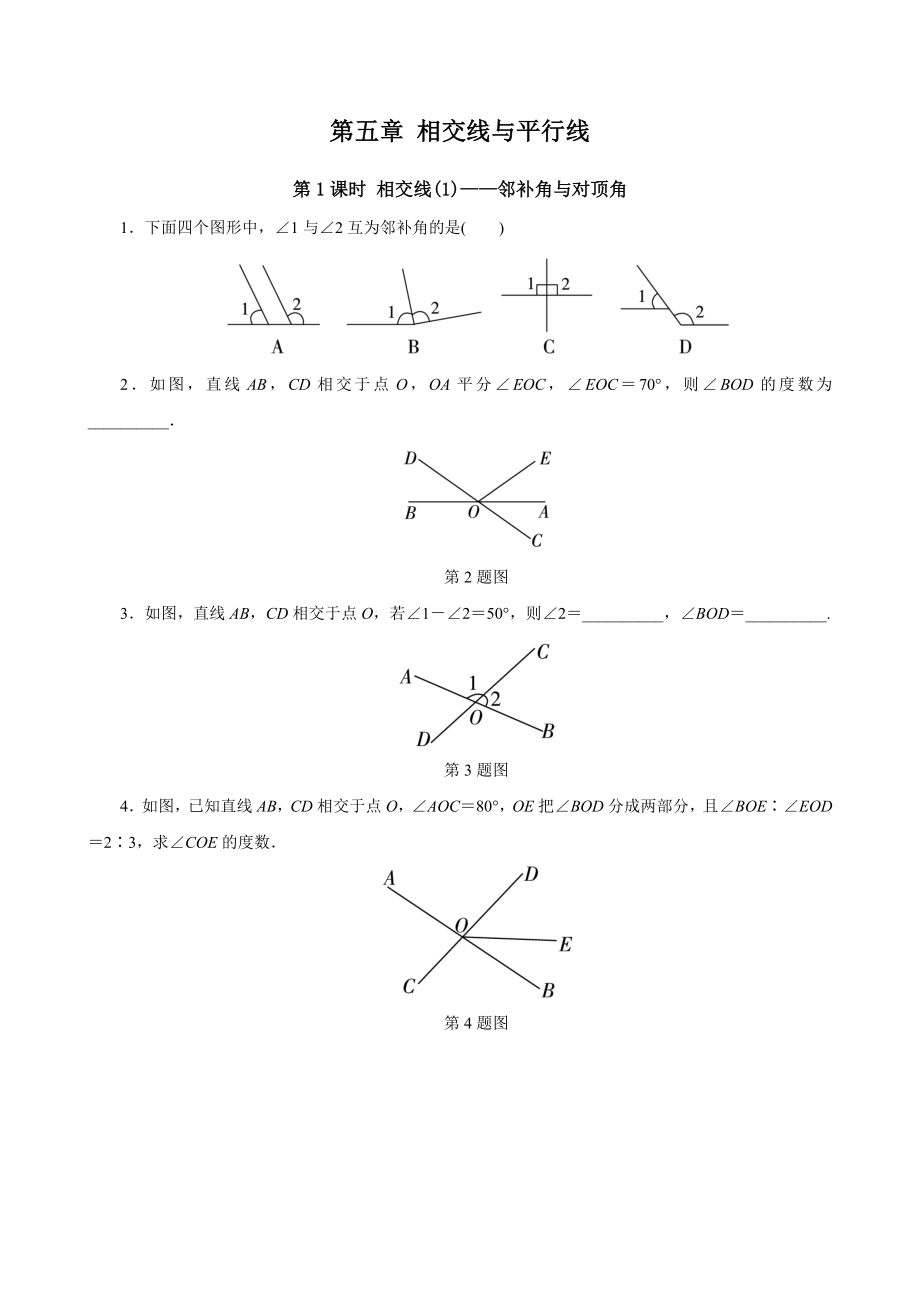
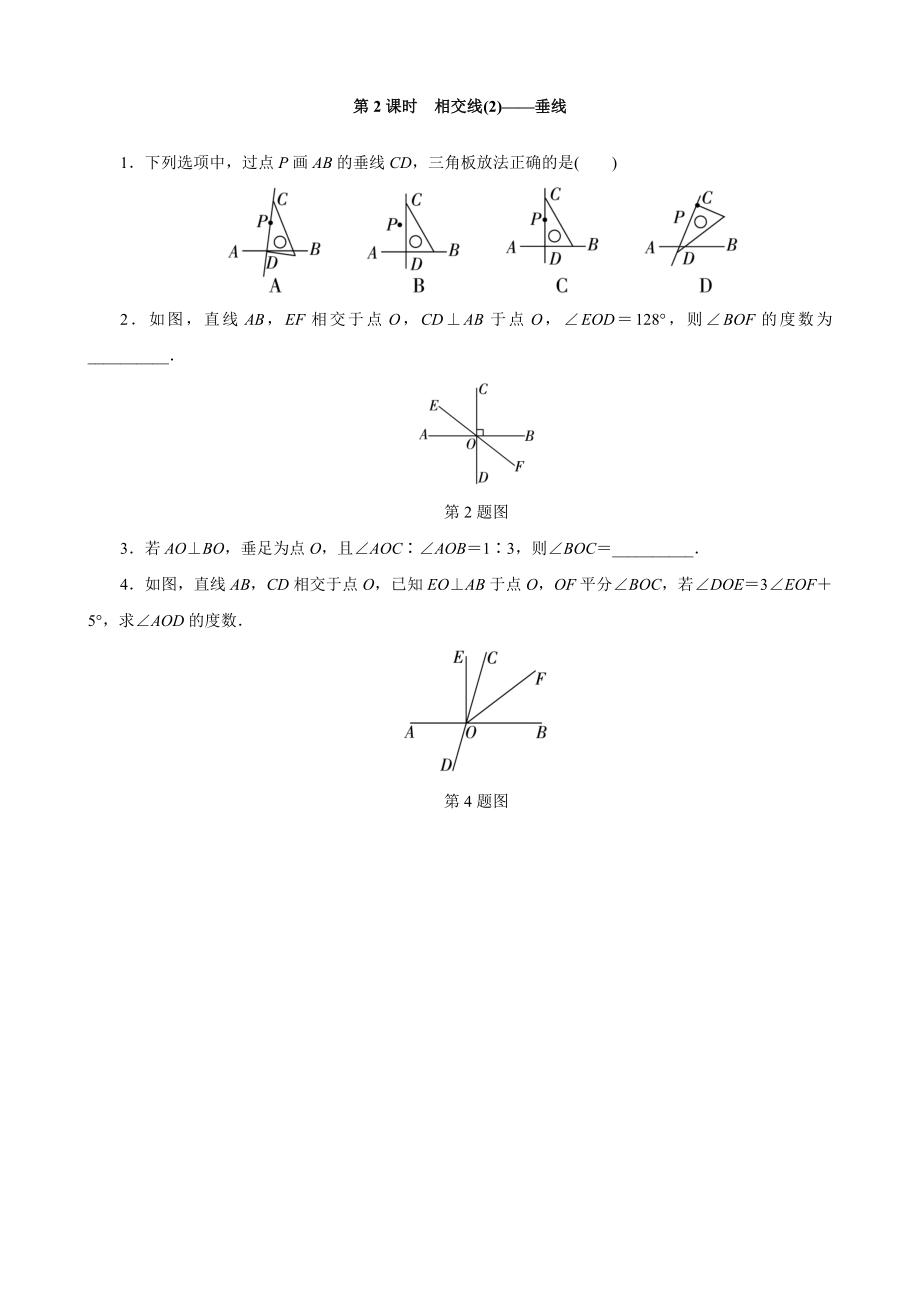
1、第五章 相交线与平行线第1课时 相交线(1)邻补角与对顶角1下面四个图形中，1与2互为邻补角的是() 2如图，直线AB，CD相交于点O，OA平分EOC，EOC70，则BOD的度数为_第2题图3如图，直线AB，CD相交于点O，若1250，则2_，BOD_.第3题图4如图，已知直线AB，CD相交于点O，AOC80，OE把BOD分成两部分，且BOEEOD23，求COE的度数第4题图第2课时相交线(2)垂线1下列选项中，过点P画AB的垂线CD，三角板放法正确的是()2如图，直线AB，EF相交于点O，CDAB于点O，EOD128，则BOF的度数为_第2题图3若AOBO，垂足为点O，且AOCAOB13，则
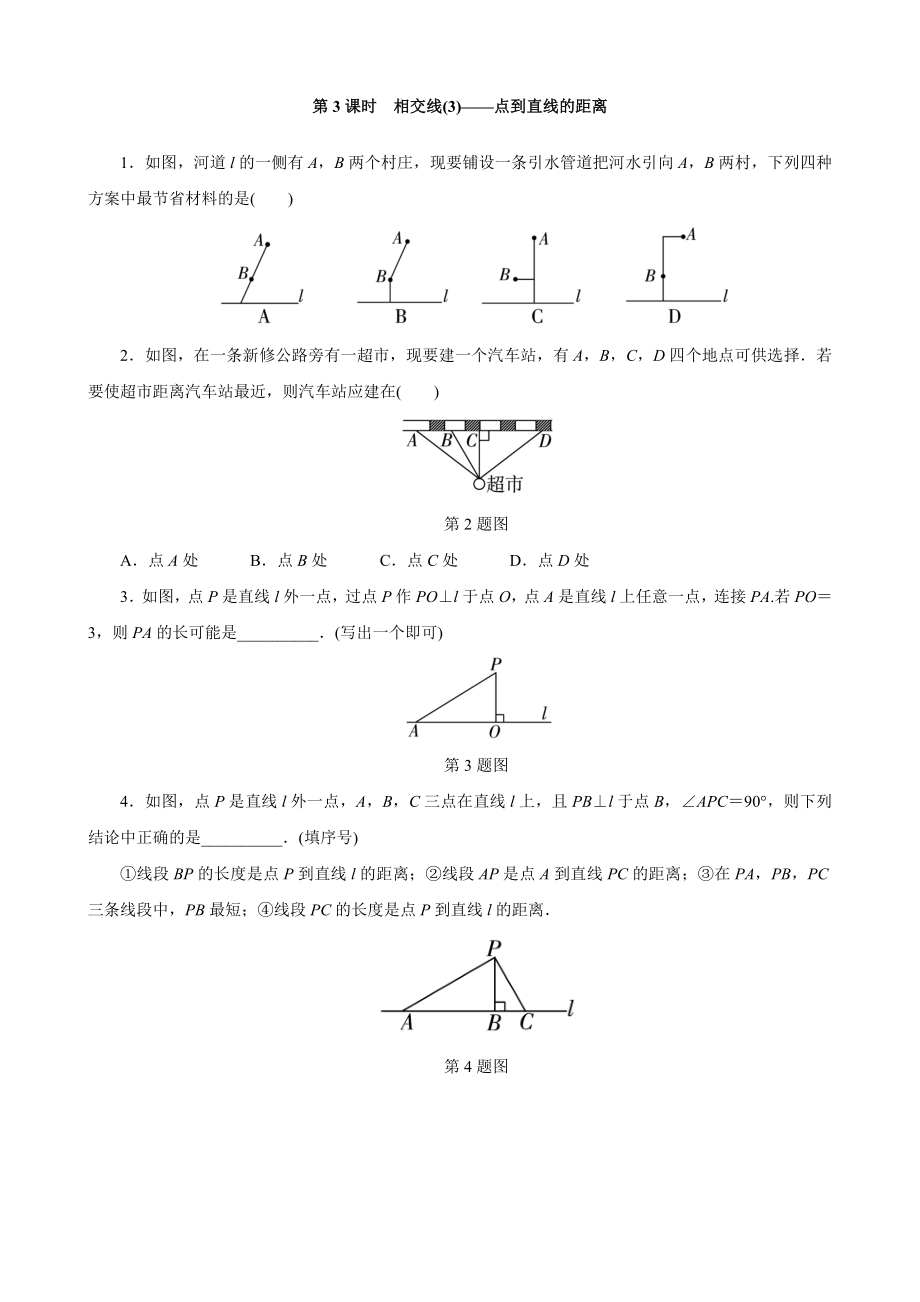
2、BOC_4如图，直线AB，CD相交于点O，已知EOAB于点O，OF平分BOC，若DOE3EOF5，求AOD的度数第4题图第3课时相交线(3)点到直线的距离1如图，河道l的一侧有A，B两个村庄，现要铺设一条引水管道把河水引向A，B两村，下列四种方案中最节省材料的是()2如图，在一条新修公路旁有一超市，现要建一个汽车站，有A，B，C，D四个地点可供选择若要使超市距离汽车站最近，则汽车站应建在()第2题图A点A处 B点B处 C点C处 D点D处3如图，点P是直线l外一点，过点P作POl于点O，点A是直线l上任意一点，连接PA.若PO3，则PA的长可能是_(写出一个即可)第3题图4如图，点P是直线l外一
3、点，A，B，C三点在直线l上，且PBl于点B，APC90，则下列结论中正确的是_(填序号)线段BP的长度是点P到直线l的距离；线段AP是点A到直线PC的距离；在PA，PB，PC三条线段中，PB最短；线段PC的长度是点P到直线l的距离第4题图第4课时 相交线(4)同位角、内错角、同旁内角1如图，1和2不是同位角的是() 2若1与2是同旁内角，135，则2的度数是()A35 B145 C35或145 D无法确定3如图，BAO和AOC是一对()第3题图A内错角 B同旁内角 C同位角 D对顶角4如图，如果2100，那么1的同位角等于_，1的内错角等于_，1的同旁内角等于_第4题图5如图(1)AB与BC
4、被AD所截得的内错角是_；(2)DE与AC被AD所截得的内错角是_；(3)1与4是直线_被直线_所截得的角；(4)B的同位角是_第5题图第5课时平行线及平行公理1在同一平面内，直线a与b相交于点M，ac，那么b与c的关系是()A平行 B相交 C平行与相交 D不能确定2下列图形中，ABCD的是()3下列说法中，正确的结论有()过一点有无数条直线与已知直线平行；如果ab，ac，那么bc；如果两线段不相交，那么它们就平行；如果两直线不相交，那么它们就平行A1个 B2个 C3个 D4个4如图，已知直线a，点B，点C.(1)请在图中过点B画出一条直线a的平行线，一共能画几条？(2)请在图中过点C画出一条
5、直线a的平行线，它与过点B的平行线平行吗？第4题图第6课时平行线的判定(1)1下列图形中，由12能得到ABCD的是()2如图，下列条件中可以判定DEAB的是()AEDCA BEDCECECDE DEBCE第2题图3如图，小明把一副三角板摆放在桌面上，其中边BC，DF在同一条直线上，可以得到一组平行线为：_，依据是_第3题图4如图，给出下列条件：34；12；4BCD180，且D4；35180.其中能推出ADBC的条件有_(填序号)第4题图第7课时平行线的判定(2)1如图，AF与BD相交于点C，BACB，且CD平分ECF.求证：ABCE.第1题图请完成下列推理过程，并将依据填在括号内的横线上证明：
6、CD平分ECF，ECD_(_)ACBFCD，(_)ECDACB.(等量代换)BACB，B_(_)ABCE.(_)2如图，已知BE平分ABD，DE平分CDB，且1与2互余，试判断直线AB，CD是否平行，为什么？ 第2题图第8课时平行线的性质1如图，直线ABCD，直线EF分别与直线AB，CD相交于点G，H.若1135，则2的度数为()第1题图A65 B55 C45 D352如图，将一把含30角的三角尺放置在长方形纸片的内部，三角尺的三个顶点恰好在长方形的边上，若GFC64，则AEF_第2题图3如图，点D，E分别在AB，BC上，DEAC，AFBC.若170，求2的度数第3题图第9课时平行线的判定与性
7、质1如图，直线a，b与直线c，d相交，已知12，3110，则4的度数为()第1题图A. 70 B. 80 C. 110 D. 1002. 如图，在四边形ABCD中，ABCD，B60.当D_时，ADBC. 第2题图3如图，直线l1，l2被直线l3所截，l3分别交l1，l2于点A和点B，过点B的直线l4交l1于点C.若1130，260，350，则4_第3题图4如图，已知ABBF，CDBF，1 2，求证：3E. 第4题图第10课时 命题、定理、证明1. 下列命题是真命题的有() 有一条公共边的角叫做邻补角；若两个角是直角，则这两个角相等；直线外一点到这条直线的垂线段的长度，叫做点到直线的距离. A.
8、 0个 B. 1个 C. 2个 D. 3个2“相交的两条直线一定不平行”，这个命题的条件是_，结论是_，这个命题是_命题3补充下列推理过程，并将依据填在括号内的横线上已知：如图，点E在直线DF上，点B在直线AC上，12，34，求证：AF.第3题图证明：12，(已知)2DGF，(_)1DGF.(_)_(同位角相等，两直线平行)3C180.( _)又34，(已知)4C180.(等量代换)ACDF.(_)AF.(_)第11课时平移的概念及性质1“水是生命之源，滋润着世间万物”国家节水标志由水滴、手掌和地球组合变形而成，寓意为像对待掌上明珠一样，珍惜每一滴水！以下通过平移节水标志得到的图形是()2如图
9、，在三角形ABC中，BC5，ABC90，将三角形ABC沿BC所在的直线向右平移得到三角形DEF，CF3，下列结论中错误的()第2题图AEC3 BAD CACDF DDEF903如图，将三角形ABC沿着射线AC的方向平移到三角形CDE的位置，连接BD.若AE12 cm，则线段BD的长是_cm.第3题图4如图，长方形BBCC的边BC长为4 cm.将三角形ABC沿边BB的方向平移2 cm得到三角形ABC，则阴影部分的面积为_cm2.第4题图5一副直角三角板按如图方式摆放，其中A30，DFE45，点C与点E重合，边BC与EF都在直线l上将三角形ABC沿直线l向右平移得到三角形ABC，当边AC经过点D时
10、，EDC_.第5题图第12课时平移作图及应用1在如图所示的草坪上，铺设一条水平宽度为2的小路，则草坪的面积为_第1题图2夏季荷花盛开，为便于游客领略“人从桥上过，如在河中行”的美好意境，某景点拟在如图所示的长方形荷塘上架设小桥若荷塘周长为300 m，则小桥总长为_m(桥宽忽略不计)第2题图3如图，网格中每个小正方形的边长都为1，三角形ABC的顶点都在格点(网格线的交点)上将三角形ABC向上平移5格，得到三角形A1B1C1.(1)请在图中画出平移后的三角形A1B1C1；(2)四边形BB1C1C的面积等于_.第3题图第六章 实数第1课时算术平方根1.的值是()A6 B6 C D2如果a有算术平方根
11、，那么a一定是()A正数 B0 C非负数 D非正数32的算术平方根是_，是_的算术平方根4一个正方形的面积为7，则它的边长为_5比较大小：(1)3_；(2)1_1.6求下列各式的值(1)； (2)；(3)； (4).第2课时平方根1.的平方根是()A B C D2(6)2的平方根是()A6 B36 C6 D3下列说法错误的是()A0的平方根是0 B4的平方根是2C64的平方根是8 D2是4的平方根4填空：(1)2.25的平方根是_；(2)已知x1的平方根是5，则x_；(3)若4x225，则x_5正数a的两个平方根分别是2m，5m，则正数a_6求下列各式的值(1)； (2)；(3)； (4).第
12、3课时立方根1.的立方根是()A B C D2立方根与它本身相同的数是()A0或1 B0或1 C0或1 D03下列说法正确的是()A1是1的平方根 B1是1的算术平方根C1是1的立方根 D1没有立方根4填空：(1)512的立方根是_；(2)_的立方根是；(3)若125x3270，则x_5已知a的算术平方根是3，b的立方根是2，则ab的值为_6求下列各式的值(1)； (2)；(3)； (4).第4课时实数(1)实数的概念及分类1下列实数中，是无理数的是()A2 B3.14 C D2在实数0.1，中，有理数的个数是()A4 B5 C3 D23已知m，则m的值所在的范围是()A0m1 B1m2 C2
13、m3 D3m44数轴上到原点的距离等于的数是_5如图，将数，表示在数轴上，其中能被墨迹覆盖的数是_第5题图6比较大小：(1)2_；(2)_.7将下列各数按要求填在横线上：1，0.7 ，.(1)无理数：_；(2)分数：_；(3)负实数：_第5课时实数(2)实数的相关性质及运算1若实数a的相反数是3，则a的值为()A3 B0 C D32计算：|()A B C5 D53下列运算正确的是()A B(1)1C5 D|3.14|3.144填空：(1)的相反数是_；(2)2的绝对值是_；(3)|3|4|_5计算：(1)|1|；(2)|.第七章 平面直角坐标系第1课时有序数对1家长会前，四个孩子分别向家长描述
14、自己在班里的座位，家长能准确找到自己孩子座位的是()A小明说他坐在第1排 B小白说她坐在第3列C.小清说她坐在第2排第5列 D小楚说他的座位靠窗2会议室2排3号记作(2，3)，那么3排2号记作()A(3，2) B(2，3)C(3，2) D(2，3)3下列说法正确的是()A数对(2，3)和(3，2)表示的位置相同B数对(2，3)和(3，2)表示的位置不同C数对(2，2)和(2，2)表示的位置不同D数对(m，n)和(n，m)表示的位置不同4如图，若的位置为(3，1)，则的位置是_.第4题图5如图，小明从点O出发，先向西走40米，再向南走30米到达点M.如果点M的位置用(40，30)表示，那么(20
15、，10)表示的是点_.第5题图第2课时平面直角坐标系(1)1如图，下列说法正确的是()第1题图A点A的横坐标是2 B点A的横坐标是1C点A的坐标是(2，1) D点A的坐标是(2，1)2若m0，n0，则在平面直角坐标系中，点P(m，n)在()A第一象限 B第二象限 C第三象限 D第四象限3若点P(m3，m1)在x轴上，则点P的坐标为()A(0，2) B(2，0) C(4，0) D(0，4)4若点P(m1，m)在第四象限内，则点Q(3，m2)在第_象限内5如图，在平面直角坐标系中(1)写出图中A，B，C，D各点的坐标；(2)描出点E(1，0)，F(1，3)，G(3，0)，H(1，3)；(3)顺次连
16、接A，B，C，D各点，直接写出围成的封闭图形是什么形状？第5题图第3课时平面直角坐标系(2)1点P(3，10)到x轴、y轴的距离分别为()A10，3 B3，10 C3，10 D10，32若点P是第二象限内的点，且点P到x轴的距离是2，到y轴的距离是3，则点P的坐标是()A(2，3) B(2，3) C(3，2) D(3，2)3若直线l平行于x轴，则直线l上A，B两点的坐标关系是()A横坐标相等 B纵坐标相等C横坐标的绝对值相等 D纵坐标都等于04若点A(m2，22m)在第一、三象限的角平分线上，则m的值为_.5已知点P(2x6，3x1)，求下列情形下点P的坐标(1)点P在y轴上；(2)点P到x轴
17、、y轴的距离相等，且点P在第二象限；(3)点P在过点A(2，4)且与y轴平行的直线上第4课时用坐标表示地理位置1已知生态园位于县城东北方向5千米处，则下列表示正确的是()2五子棋的比赛规则是只要同色的5个棋子先连成一条直线就算获胜如图是两人玩的一盘棋，若白1的位置是(1，1)，黑2的位置是(2，0)，现轮到黑棋走，则黑棋要获得胜利可以放在()第2题图A(2，5) B(3，4) C(7，0) D(7，1)3如图是某地学校、电影院、体育馆和超市的大致位置示意图，1个单位长度代表1米若小李从体育馆向南走150米，再向东走400米，再向南走250米，再向西走50米，最终到达的地点是_.第3题图4如图是
18、某校的平面示意图，已知图书馆(3，2)，行政楼(2，3).第4题图(1)根据所给条件建立适当的平面直角坐标系；(2)写出实验楼、校门口、综合楼、信息楼的坐标；(3)在图中用点P表示体育馆(1，3)的位置第5课时用坐标表示平移1将点A(2，3)沿y轴正方向平移4个单位长度得到点A，则点A的坐标为()A(2，7) B(2，1) C(6，3) D(2，3)2将点A(x，y)先向左平移2个单位长度，再向下平移3个单位长度，得到的点的坐标是()A(x2，y3) B(x2，y3)C(x2，y3) D(x2，y3)3如图，将线段AB平移得到线段CD，使得点A与点C(4，2)重合，则点B的对应点D的坐标是()
19、第3题图A(7，3) B(6，4)C(7，4) D(8，4)4在平面直角坐标系中，点M(x，y)经过平移后可以得到点N(xa，yb)，则该点的平移过程为_5如图，已知三角形ABC经过平移后得到三角形DEF，点A与点D，点B与点E，点C与点F分别对应，已知A(3，3)，D(2，1).第5题图(1)在平面直角坐标系中画出平移后的三角形DEF；(2)写出以下点的坐标：B_，C_，E_，F_；(3)若点P(x，y)通过上述平移得到的对应点为Q(3，5)，则点P的坐标为_.第八章 二元一次方程组第1课时二元一次方程组1下列方程组中，属于二元一次方程组的是()A BC D2已知关于x，y的方程axy3x1
20、是二元一次方程，则a满足的条件是()Aa0 Ba1 Ca3 Da13下列各组数中，是二元一次方程2x5y4的解的是()A B C D4若是方程2xy0的解，则6a3b2_5已知方程组的解是其中“”和“”分别代表某个数字，求的值第2课时解二元一次方程组(1)代入消元法1在运用代入消元法解二元一次方程组的过程中，下列变形能使代入后化简比较简便的是()Ax ByCx Dy2x52利用代入消元法解方程组时，把方程代入方程，结果正确的是()Ax2x11 Bx2x11Cx2x11 Dx2x113二元一次方程组的解为_4用代入消元法解下列方程组：(1) (2) 第3课时解二元一次方程组(2)加减消元法1对于
21、方程组用加减消元法消去x得到的方程是()A.3y2 B3y32C11y32 D12y22二元一次方程组的解是()A B C D3已知二元一次方程组则(xy)2_4用加减消元法解下列方程组：(1) (2)第4课时实际问题与二元一次方程组(1)和差倍分问题14月23日是世界读书日甲、乙两位同学在读书日到来之际共购买图书22本，其中甲同学购买的图书数量比乙同学购买的图书数量的2倍多1本，求甲、乙两位同学分别购买的图书数量设甲同学购买图书x本，乙同学购买图书y本，则可列方程组为()A B C D2为了节省空间，家里的饭碗一般是摞起来存放的，如果5只饭碗摞起来的高度为13 cm，9只饭碗摞起来的高度为2
22、0 cm，李老师家碗橱每格的高度为30 cm，则李老师家碗橱一格最多只能放_只碗3算法统宗中记录了“百僧分馒”问题：一百馒头一百僧，大和三个更无争，小和三人分一个，大和小和得几丁？意思是：100个和尚分100个馒头，大和尚1人吃3个馒头，小和尚3人吃1个馒头，问大、小和尚各有几人？第5课时实际问题与二元一次方程组(2)配套与几何问题1某校定制校庆纪念品，一套纪念品由2枚纪念币和3枚定制书签组成，定制一枚纪念币需要花费15元，一枚书签需要花费10元若学校一共花费了5 400元，且纪念币和定制书签刚好配套，求该学校定制纪念币和书签各多少枚2小明在拼图时，发现8个大小一样的长方形按如图1所示的方式摆
23、放，恰好可以拼成一个大的长方形，小红看见了，说“我来试一试”结果小红七拼八凑，拼成如图2所示的正方形，中间还留了一个洞，恰好是边长为2 cm的小正方形！请求出图2这个正方形的面积第2题图第6课时实际问题与二元一次方程组(3)经济问题1某公司用3 000元购进两种货物货物全部卖出后，一种货物的利润率是10%，另一种货物的利润率是11%，两种货物共获利315元若设该公司购进这两种货物所用的费用分别为x元、y元，则列出的方程组是()ABCD2嘉琪记录了她连续两天陪妈妈去水果店买水果的账目：第一天买了2斤香蕉和1斤苹果，共花了11元，第二天买了1斤香蕉和3斤苹果，共花了43元已知两天中，香蕉和苹果的单
24、价相同她的记录是否正确？若正确，请算出香蕉和苹果的单价；若错误，请说明理由第7课时实际问题与二元一次方程组(4)工程与行程问题1某同学家离学校8千米，每天骑自行车上学和放学有一天上学时顺风，从家到学校共用时25分钟，放学时逆风，从学校回家共用时35分钟已知该同学在无风时骑自行车的速度为x千米/时，风速为y千米/时，则根据题意，可列方程组为_(注意单位统一)2为实施乡村振兴战略，解决某山区老百姓出行难的问题，当地政府决定修建一条高速公路其中一段长为146米的山体隧道贯穿工程由甲、乙两个工程队负责施工甲工程队独立施工2天后，乙工程队加入，两工程队又联合施工了1天，这3天共施工26米已知甲工程队每天
25、比乙工程队多施工2米，按此速度完成这项隧道贯穿工程，甲、乙两个工程队还需联合施工多少天？*第8课时三元一次方程组的解法及其应用1三元一次方程组的解是()A B C D2解方程组：3我国古代数学专著九章算术中有一题，其大致意思为：用卖2头牛、5头羊的钱买13头猪，剩钱1 000；用卖3头牛、3头猪的钱买9头羊，钱正好；用卖6头羊、8头猪的钱买5头牛，还差钱600.求每头牛、羊、猪的价钱第九章 不等式与不等式组第1课时不等式及其解集1下列式子是不等式的是()Ax2y1 Bx Cx2y Dx302用不等式表示如图所示的解集为()第2题图Ax2 Bx2 Cx2 Dx23下列各数中，使不等式 x24成立
26、的是()A1 B0 C2 D54某种牛奶包装盒上标明“净重205 g，蛋白质含量3%”，则一盒这种牛奶中蛋白质的质量是()A3%以上 B6.15 gC6.15 g及以上 D不足6.15 g5用适当的不等式表示下列关系：(1)x是非正数：_； (2)x与2的差小于15：_；(3)x与y的2倍的和不小于5：_6将下列不等式的解集在数轴上表示出来，并填空：(1)x1; (2)x1； 最小整数解为_ 最大整数解为_(3)x3; (4)x3. 负整数解为_ 非负整数解为_第2课时不等式的性质1(2022杭州)已知a，b，c，d是实数若ab，cd，则()Aacbd BabcdCacbd Dabcd2下列不
27、等式变形正确的是()A由2xx1，得2xx1 B由2x3，得x32C由3x6，得x2 D由2x3，得x3根据机器零件的设计图纸(如图)，用不等式表示零件长度的合格尺寸(L的取值范围)为_第3题图4已知xy，用“”“”填空：(1)x5_y5; (2)4x_4y；(3)xy_2y; (4)_；(5)3x2_3y2.5若ab，则am2_bm2.(填“”“”“”或“”)6利用不等式的性质解下列不等式，并把解集在数轴上表示出来(1)x97； (2)4x10； (3)3x15.第3课时一元一次不等式的概念及解法(1)1下列各式中，是一元一次不等式的是()Ax21 B0 C5 Dxy12不等式x13x3的解
28、集在数轴上表示正确的是()3写出一个解集为x3的一元一次不等式：_4不等式33x2(12x)的解集是_5解下列不等式，并把解集在数轴上表示出来(1)5x12x7；(2)2x63(x1)；(3)9(x1)4.第4课时一元一次不等式的概念及解法(2)1不等式 0的解集是()Ax Bx1 Cx2 Dx22不等式3x7x的非负整数解有()A1个 B2个 C3个 D4个3某同学解不等式 的步骤如下：去分母，得3(4x)2(2x3)；去括号，得123x4x6；移项，得3x4x612；系数化为1，得x18.其中错误的步骤是()A B C D4解下列不等式，并把解集在数轴上表示出来(1)； (2)1.5求不等
29、式 1的正整数解第5课时一元一次不等式的应用(1)1小明用30元购买铅笔和签字笔，已知铅笔和签字笔的单价分别是2元和5元，他买了2支铅笔后，最多还能买几支签字笔？设小明还能买x支签字笔，则下列不等关系正确的是()A522x30 B522x30C222x30 D225x302某中学为了熏陶师生的爱国情怀，组织师生观看以抗美援朝真实战役为背景拍摄的电影长津湖该校先组织七年级部分师生共100人进行观影活动已知学生票每张24元，教师票每张30元，若总费用不超过2 440元，最多可以安排几名教师参加这次观影活动？3某工程队计划招聘从事甲、乙两种工作的工人共150名，设从事甲工作的人数为x.(1)若招聘的
30、工人中，从事乙工作的人数是从事甲工作人数的2倍，设从事乙工作的人数为y，则从事甲、乙工作的人数各有多少？(请列方程组进行解答)(2)若招聘的工人中，从事乙工作的人数至少比从事甲工作的人数多25，则最多有多少人从事甲工作？(请列不等式进行解答)第6课时一元一次不等式的应用(2)1某市政府致力于建设“智慧城市”来优化旅游环境，在景区步行街内投入了26台“智能机器人导游”，它可以讲解、互动和代步，赢得了游客的喜爱已知甲型机器人每台的价格是6万元，乙型机器人每台的价格是4万元该市政府计划用不超过39万元再次购买这两种型号的机器人共8台(两种都购买)，则共有哪几种购买方案？2某校为做好新型冠状病毒感染的
31、预防工作，计划为教职工购买一批洗手液(每人1瓶).学校派王老师去商场购买，他在商场了解到，某个牌子的洗手液售价为每瓶14元，现有两种优惠活动活动一：一律打九折；活动二：当购买量不超过50瓶时，按原价销售；当购买量超过50瓶时，超过的部分打八折如果该校共有m名教职工，请你帮王老师设计最省钱的购买方案第7课时一元一次不等式组的概念及解法(1)1下列选项中是一元一次不等式组的是()A B C D2“a与5的和是正数且a的一半不大于3”用不等式组表示为()A. B C D3某不等式组的解集在数轴上的表示如图所示，则该不等式组的解集为()第3题图Ax4 Bx2 Cx2 D2x44不等式组的解集在数轴上表
32、示为()5解下列不等式组：(1) (2)第8课时一元一次不等式组的解法(2)1不等式组的解集是()Ax3 B无解 Cx4 D3x42不等式组的整数解的个数是()A6 B5 C4 D33如图为某不等式组的解集在数轴上的表示，则这个不等式组可能是()第3题图A. BC D.4解不等式组：5解不等式组：并把它的解集在数轴上表示出来第9课时一元一次不等式组的应用1某校组织学生进行经典图书阅读，七(一)班老师从图书室借了一批书分给班里学生阅读，每人5本，则余9本；每人7本，则最后一个同学能得到书但不足4本，这批书有多少本？2某小区积极响应创建全国卫生城市活动，决定在小区内安装垃圾分类的温馨提示牌和垃圾箱
33、已知温馨提示牌的单价是50元，垃圾箱的单价是150元该小区至少需要安放48个垃圾箱，如果购买温馨提示牌和垃圾箱共100个，且费用不超过10 000元，请你列举出所有购买方案，并指出哪种方案所需资金最少？最少是多少元？第十章 数据的收集、整理与描述第1课时统计调查(1)数据的收集1为了了解某年级学生每天参加体育锻炼的时间，比较恰当的收集数据的方法是()A查阅资料 B问卷调查 C直接观察 D实验2调查收集数据时，一般要设计调查问卷设计的调查问卷中应包括()A调查的问题和调查的对象B调查的目的和调查的内容C调查的方法D以上内容都应具备3小芸为了解同学们最感兴趣的在线学习方式，设计了如下的调查问卷(选项不完整)：她准备从“在线听课；在线讨论；在线学习23小时；用手机在线学习；在线阅读”中选取三个作为该问题的选项内容，合理的选取是_(填序号)4卫生部门为了了解当地青少年身体发育受哪些因素影响，请你设计一份问卷进行调查，那么你的问卷中会涉及哪几个方面的问题？(如：你偏食吗)(1)_；(2)_(至少要提出两个问题)第2课时统计调查(2)数据的整理与描述1某图书管理员将甲、乙、丙三类书籍的有关数据制成如图所示的不完整的扇形统计图，
