1、2023年浙江省绍兴市中考数学模拟试卷（二）一、选择题（本大题有10小题，每小题4分，共40分）1. 全国统一规定的交通事故报警电话是（ ）A. 122B. 110C. 120D. 1142. 国家统计局发布数据，去年一季度国内生产总值270178亿元同比增长4.8%，比前年四季度环比增长1.3%把27017800000000用科学记数法表示为（ ）A. B. C. D. 3. 下列图形：其中轴对称图形的个数是（ ）A. 4B. 3C. 2D. 14. 如图，数轴上的点P表示下列四个无理数中的一个，这个无理数是（ ）A. B. C. D. 5. 下列计算错误的是（ ）A. B. C. D. 6
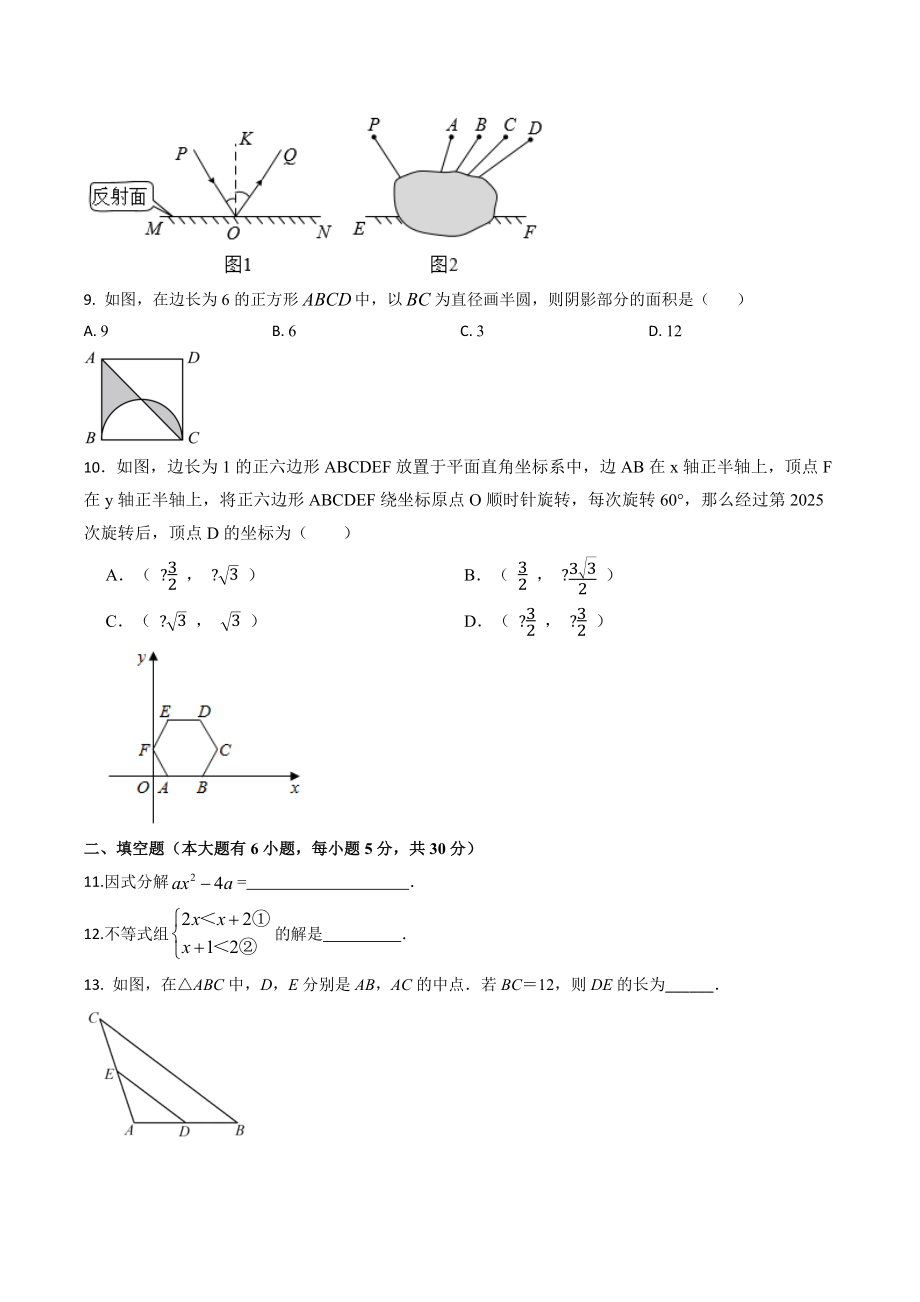
2、. 统计一名射击运动员在某次训练中10次射击的中靶环数，获得如下数据：7，8，10，9，9，8，10，9，9，10这组数据的众数是（ ）A. 7B. 8C. 9D. 107. 为了增强学生的安全防范意识，某校初三（1）班班委举行了一次安全知识抢答赛，抢答题一共20个，记分规则如下：每答对一个得5分，每答错或不答一个扣1分小红一共得70分，则小红答对的个数为（ ）A. 14B. 15C. 16D. 178. 图1是光的反射规律示意图其中，PO是入射光线，OQ是反射光线，法线KOMN，POK是入射角，KOQ是反射角，KOQPOK图2中，光线自点P射入，经镜面EF反射后经过的点是( )A. A点B.
3、 B点C. C点D. D点9. 如图，在边长为6的正方形中，以为直径画半圆，则阴影部分的面积是（ ）A. 9B. 6C. 3D. 1210如图，边长为1的正六边形ABCDEF放置于平面直角坐标系中，边AB在x轴正半轴上，顶点F在y轴正半轴上，将正六边形ABCDEF绕坐标原点O顺时针旋转，每次旋转60，那么经过第2025次旋转后，顶点D的坐标为（） A（ ?32 ， ?3 ）B（ 32 ， ?332 ）C（ ?3 ， 3 ）D（ ?32 ， ?32 ）二、填空题（本大题有6小题，每小题5分，共30分）11.因式分解= 12.不等式组的解是 13. 如图，在ABC中，D，E分别是AB，AC的中点若
4、BC12，则DE的长为_14. 如图四边形ABCD是平行四边形，CD在x轴上，点B在y轴上，反比例函数的图象经过第一象限点A，且平行四边形ABCD的面积为6，则_15. 如图，某一时刻太阳光从窗户射入房间内，与地面的夹角，已知窗户的高度，窗台的高度，窗外水平遮阳篷的宽，则的长度为_（结果精确到）16. 如图，在等腰直角三角形中，点，分别为，上的动点，且，当的值最小时，的长为_三、解答题（本大题有8小题，第1720小题每小题8分，第21小题10分，第22，23小题每小题12分，第24小题14分，共80分解答需写出必要的文字说明、演算步骤或证明过程）17. 计算：圆圆在做作业时，发现题中有一个数字
5、被墨水污染了（1）如果被污染的数字是，请计算（2）如果计算结果等于6，求被污染的数字18. （1）计算：（2）先化简，再求值：，其中19. 某校为满足学生课外活动的需求，准备开设五类运动项目，分别为A：篮球，B：足球，C：乒乓球，D：羽毛球，E：跳绳为了解学生的报名情况，现随机抽取八年级部分学生进行调查，并根据调查结果绘制了如下两幅不完整的统计图请根据以上图文信息回答下列问题：（1）此次调查共抽取了多少名学生？（2）请将此条形统计图补充完整；（3）在此扇形统计图中，项目D所对应的扇形圆心角的大小为_；（4）学生小聪和小明各自从以上五类运动项目中任选一项参加活动，请利用画树状图或列表的方法求他俩
6、选择相同项目的概率20. 如图，已知AC为的直径，直线PA与相切于点A，直线PD经过上的点B且，连接OP交AB于点M求证：（1）PD是的切线；（2）21. 某校组织学生从学校出发，乘坐大巴前往基地进行研学活动大巴出发1小时后，学校因事派人乘坐轿车沿相同路线追赶已知大巴行驶的速度是40千米/小时，轿车行驶的速度是60千米/小时（1）求轿车出发后多少小时追上大巴？此时，两车与学校相距多少千米？（2）如图，图中OB，AB分别表示大巴、轿车离开学校的路程s（千米）与大巴行驶的时间t（小时）的函数关系的图象试求点B的坐标和AB所在直线的解析式；（3）假设大巴出发a小时后轿车出发追赶，轿车行驶了1.5小时
7、追上大巴，求a的值22. 如图:（1）将两张长为8，宽为4的矩形纸片如图1叠放判断四边形AGCH的形状，并说明理由；求四边形AGCH的面积（2）如图2，在矩形ABCD和矩形AFCE中，AB2，BC7，CF，求四边形AGCH的面积23. 问题探究（1）在中，分别是与的平分线若，如图，试证明；将中的条件“”去掉，其他条件不变，如图，问中的结论是否成立？并说明理由迁移运用（2）若四边形是圆的内接四边形，且，如图，试探究线段，之间的等量关系，并证明24. 已知：经过点，（1）求函数解析式；（2）平移抛物线使得新顶点为（m0）倘若，且在的右侧，两抛物线都上升，求的取值范围；在原抛物线上，新抛物线与轴交于
8、，时，求点坐标参考答案一、选择题（本大题有10小题，每小题4分，共40分）1. A2. B3. B4. B5. D6. C7. B8. B9. A10A二、填空题（本大题有6小题，每小题5分，共30分）11.12.13. 614. 615. 4.4m【详解】解：根据题意得：ADCP，DPC=30，ADB=30，AF=2m，CF=1m，BC=AF+CF-AB=2.54m，即的长度为4.4m故答案为：4.4m.16. 【详解】如图，过点作，且，连接，如图1所示，又，当三点共线时，取得最小值，此时如图2所示，在等腰直角三角形中，设，即取得最小值时，CM的长为，故答案为：三、解答题（本大题有8小题，第
9、1720小题每小题8分，第21小题10分，第22，23小题每小题12分，第24小题14分，共80分解答需写出必要的文字说明、演算步骤或证明过程）17. （1）解：；（2）设被污染的数字为x，由题意，得，解得，所以被污染的数字是318. （1）解：原式；（2）解：原式当时，原式19. （1）1010%=100（人）（2）C组的人数为：100-20-30-15-10=25（人）补全条形图如图所示：（3）D组对应的度数为：（4）画树状图如图所示：相同的有：AA、BB、CC、DD、EE五种情况；共有25种情况，故相同的情况概率为：20. （1）连接OB， AC为的直径， PD是的切线；（2）直线PA与
10、相切于点A，PD是的切线，21. (1)解：设轿车行驶时间为x小时，则大巴行驶的时间为小时根据题意，得:,解得x2则(千米)，轿车出发后2小时追上大巴，此时，两车与学校相距120千米（2）解：轿车追上大巴时，大巴行驶了3小时，点B的坐标是由题意，得点A的坐标为设AB所在直线的解析式为，则：解得k60，b60AB所在直线的解析式为s60t60（3）解：由题意，得，解得：，故a的值为小时22. （1）四边形ABCD，四边形AECF都是矩形 四边形AHCG为平行四边形 四边形AHCG为菱形；设AH=CG=x，则DH=AD-AH=8-x在中即 解得 四边形AHCG的面积为；（2）由图可得矩形ABCD和
11、矩形AFCE对角线相等 设AH=CG=x则HD=7-x在中， 在中， EC=EH+CH=8x=3四边形AGCH的面积为23. （1），又、分别是、的平分线点D、E分别是、的中点，结论成立，理由如下：设与交于点F，由条件，得，又在上截取由BF=BF，又CF=CF，（2），理由如下：四边形是圆内接四边形，作点B关于的对称点E，连结，的延长线与的延长线交于点M，与交于点F，AE、DC分别是、的角平分线由得24. （1）解：把，代入，得，解得：，函数解析式为：；（2）解：，顶点坐标为(0，-3)，即点B是原抛物线的顶点，平移抛物线使得新顶点为（m0）抛物线向右平移了m个单位，m=2，平移抛物线对称轴为直线x=2，开口向上，在的右侧，两抛物线都上升，又原抛物线对称轴为y 轴，开口向上，k2，把P（m，n）代入，得n=，P（m， ）根据题意，得新抛物线解析式为：y=(x-m)2+n=x2-mx+m2-3，Q(0，m2-3)，B（0，-3），BQ=m2，BP2=，PQ2=，BP=PQ，如图，过点P作PCy轴于C，则PC=|m|，BP=PQ，PCBQ，BC=BQ=m2，BPC=BPQ=120=60，tanBPC= tan 60=，解得：m=2（舍去负数），n=3，故P的坐标为（2，3）.
