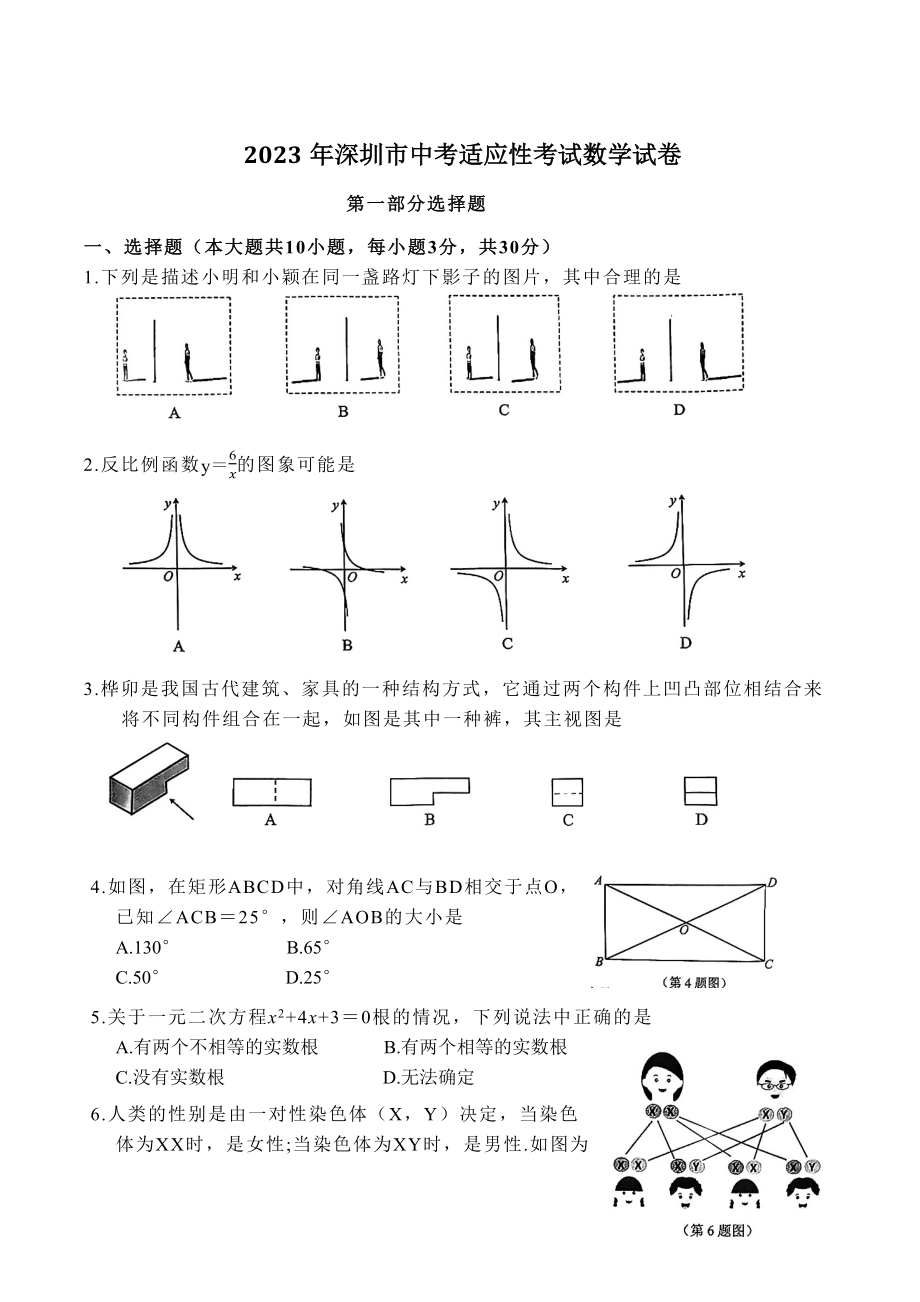
1、 2023年深圳市中考适应性考试数学试卷第一部分选择题一、选择题（本大题共10小题，每小题3分，共30分）1.下列是描述小明和小颖在同一盏路灯下影子的图片，其中合理的是2.反比例函数y6x的图象可能是3.桦卯是我国古代建筑、家具的一种结构方式，它通过两个构件上凹凸部位相结合来将不同构件组合在一起，如图是其中一种裤，其主视图是4.如图，在矩形ABCD中，对角线AC与BD相交于点O，已知ACB25，则AOB的大小是A.130 B.65C.50 D.255.关于一元二次方程x2+4x+30根的情况，下列说法中正确的是A.有两个不相等的实数根 B.有两个相等的实数根C.没有实数根 D.无法确定6.人类
2、的性别是由一对性染色体（X，Y）决定，当染色体为XX时，是女性;当染色体为XY时，是男性.如图为一对夫妻的性染色体遗传图谱，如果这位女士怀上了一个小孩，该小孩为女孩的概率是A.14 B.13C.12 D.347.某品牌20寸的行李箱拉杆拉开后放置如图所示，经测量该行李箱从轮子底部到箱子上沿的高度AB与从轮子底部到拉杆顶部的高度CD之比是黄金比（约等于0.618）.已知CD80cm，则AB约是A.30cm B.49cmC.55cm D.129cm8.如图，九年级（1）班课外活动小组利用平面镜测量学校旗杆的高度，在观测员与旗杆AB之间的地面上平放一面镜子，在镜子上做一个标记E，当观测到旗杆顶端在镜
3、子中的像与镜子上的标记重合时，测得观测员的眼睛到地面的高度CD为1.6m，观测员到标记E的距离CE为2m，旗杆底部到标记E的距离AE为16m，则旗杆AB的高度约是A.22.5m B.20m C.14.4m D.12.8m9.如图，某校劳动实践课程试验园地是长为20m，宽为18m的矩形，为方便活动，需要在园地中间开辟一横两纵共三条等宽的小道.如果园地余下的面积为306m2，则小道的宽为多少？设小道的宽为xm，根据题意，可列方程为A.（20-2x）（18-x）306 B.（20-x）（18-2x）306C.2018-218x-20x+x2306 D.2018-220x-18x+x230610.如图
4、，已知正方形ABCD的边长为4，E是AB边延长线上一点，BE2，F是AB边上一点，将CEF沿CF翻折，使点E的对应点G落在AD边上，连接EG交折痕CF于点H，则FH的长是A.43 B.103 C.1 D.53第二部分非选择题二、填空题（本大题共5小题，每小题3分，共15分）11.已知x1是关于的一元二次方程x2+mx+30的一个根，则m .12.五线谱是一种记谱法，通过在五根等距离的平行横线上标以不同时值的音符及其他记号来记载音乐.如图，A，B，C为直线l与五线谱的横线相交的三个点，则ABBC的值是 .13.一个不透明的袋子里装有红、白两种颜色的球共20个，每个球除颜色外都相同，每次摸球前先把
5、球摇匀，从中随机摸出一个球，记下它的颜色后再放回袋子里，不断重复这一过程，将实验后的数据整理成下表:摸球次数501002005008001000摸到红球的频数112750124201249摸到红球的频率0.2200.2700.2500.2480.2510.249估计袋中红球的个数是 .14.如图，已知A是y轴负半轴上一点，点B在反比例函数ykx（k0）的图象上，AB交x轴于点C，OAOB，AOB120，AOC的面积为23，则k .15.如图,已知RtABC中,ACB90,E是AB的中点,过点B作BDAB,交CE的延长线于点D，若BD4，CD8，则AC_.三、解答题（本题共7小题，共55分）16
6、.（本题5分）解方程:x2-4x-120.17.（本题7分）为庆祝神舟十五号载人飞船发射取得圆满成功，某校举办了航天航空科技体验活动，内容有三项:A.聆听航天科普讲座，B.参加航天梦想营，C.参观航天科技展.每位同学从中随机选择一项参加.（1）该校小明同学选择“参加航天梦想营”的概率是 ;（2）请用列表或画树状图的方法，求该校小亮同学和小颖同学同时选择“参观航天科技展“的概率.18.（本题8分）如图，在平面直角坐标系中，ABC各顶点的坐标分别是A（4，8），B（4，4），C（10，4），A1B1C1与ABC关于原点O位似，A，B，C的对应点分别为A1，B1，C1，其中B1的坐标是（2，2）.（
7、1）A1B1C1和ABC的相似比是 ;（2）请画出A1B1C1;（3）BC边上有一点M（a，b），在B1C1边上与点M对应点的坐标是 ;（4）A1B1C1的面积是 .19.（本题8分）某商店销售一款工艺品，每件成本为100元，为了合理定价，投放市场进行试销.据市场调查，销售单价是160元时，每月的销售量是200件，而销售单价每降价1元，每月可多销售10件.设这种工艺品每件降价x元.（1）每件工艺品的实际利润为（）元（用含有x的式子表示）;（2）为达到每月销售这种工艺品的利润为15000元，且要求降价不超过20元，那么每件工艺品应降价多少元？20.（本题8分）如图，已知ABC中，D是BC边上一点
8、，过点D分别作DEAC交AB于点E,作DFAB交AC于点F,连接AD.（1）下列条件: D是BC边的中点; AD是ABC的角平分线; 点E与点F关于直线AD对称.请从中选择一个能证明四边形AEDF是菱形的条件，并写出证明过程;（2）若四边形AEDF是菱形，且AE2， CF1,求BE的长.21.（本题9分）定义在平面内，把一个图形上任意一点与另一个图形上任意一点之间的距离的最小值，称为这两个图形之间的距离.即A，B分别是图形M和图形N上任意一点，当AB的长最小时，称这个最小值为图形M与图形N之间的距离.例如，如图1，ABl1，线段AB的长度称为点A与直线h之间的距离，当l1l2时，线段AB的长度
9、也是l1与l2之间的距离.应用（1）如图2，在等腰RtBAC中，A90，ABAC，点D为AB边上一点，过点D作DEBC交AC于点E.若AB6,AD4,则DE与BC之间的距离是 ;（2）如图3，已知直线l3:y=-x+4与双曲线C:ykx（x0）交于A（1，m）与B两点，点A与点B之间的距离是 ，点O与双曲线C1之间的距离是 ;拓展（3）按规定，住宅小区的外延到高速路的距离不超过80m时，需要在高速路旁修建与高速路相同走向的隔音屏障（如图4）.有一条“东南一西北”走向的笔直高速路，路旁某住宅小区建筑外延呈双曲线的形状，它们之间的距离小于80m.现以高速路上某一合适位置为坐标原点，建立如图5所示的
10、直角坐标系，此时高速路所在直线l的函数表达式为y-x，小区外延所在双曲线C的函数表达式为y2400x（x0），那么需要在高速路旁修建隔音屏障的长度是多少？（第21题图）22.（本题10分）过四边形ABCD的顶点A作射线AM，P为射线AM上一点，连接DP.将AP绕点A顺时针方向旋转至AQ，记旋转角PAQ，连接BQ.（1）探究发现如图1，数学兴趣小组探究发现，如果四边形ABCD是正方形，且90.无论点P在何处，总有BQDP，请证明这个结论.（2）类比迁移如图2，如果四边形ABCD是菱形，DAB60，MAD15，连接PQ,当PQBQ，AB6+2时，求AP的长;（第22题图）（3）拓展应用如图3，如果四边形ABCD是矩形，AD6，AB8，AM平分DAC， 90.在射线AQ上截取AR，使得AR43AP.当PBR是直角三角形时，请直接写出AP的长.图3 备用图（第22题图）
