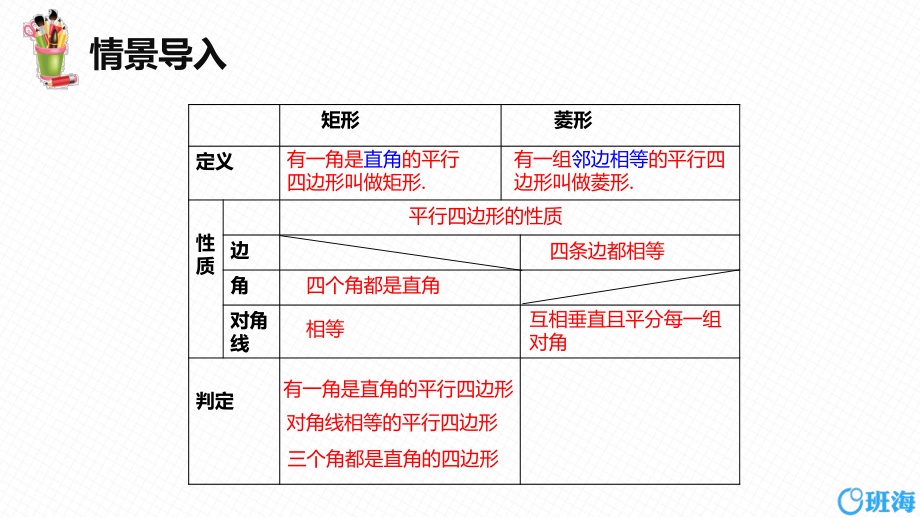
1、22.5 菱 形 第2课时 想一想：1.菱形、矩形的定义？2.它们分别比平行四边形多了哪些性质？3.怎样判定一个四边形是矩形？旧知回顾 矩形 菱形 定义 性质 边 角 对角线 判定 有一角是直角的平行四边形叫做矩形.有一组邻边相等的平行四边形叫做菱形.平行四边形的性质 四条边都相等 四个角都是直角 相等 互相垂直且平分每一组对角 有一角是直角的平行四边形 对角线相等的平行四边形 三个角都是直角的四边形 探究新知 同学们想一想，我们在学习平行四边形的判定 和矩形的判定时，我们是如何到的它们的判定方法 呢？那么类比着它们，菱形的判定方法是什么？1 知识点 由对角线的位置关系判定菱形 1.用一长一短
2、两根细木条，在它们的中点处固定一个小 钉子，做成一个可转动的十字架，四周围上一根橡 皮筋，做成一个四边形.2.任意转动木条，这个四边形 总有什么特征？你能证明你发现的结论吗？继续转 动木条，观察什么时候橡皮筋周围的四边形变成菱 形？你能证明你的猜想吗？猜想：对角线互相垂直的平行四边形是菱形.3.这个命题的前提是什么？结论是什么？用几何语言表示命题如下：已知：在ABCD 中，对角线ACBD，求证：ABCD 是菱形.分析：我们可根据菱形的定义来证明这个平行四边形 是菱形，由平行四边形的性质得到BO=DO，由 AOB=AOD=90及AO=AO，得AOB AOD，可得到AB=AD(戒根据线段垂直平分线
3、性质定理,得到 AB=AD)，最后证得ABCD 是菱形.归 纳 对角线互相垂直的平行四边形是菱形.提示：此方法包括两个条件(1)是一个平行四边形；(2)两条对角线互相垂直.对角线互相垂直且平分的四边形是菱形.例1 如图，在平行四边形ABCD 中，对角线AC，BD相交于点O，过点O 作直线EFBD，分别交AD，BC 于点E 和点F，连接BE，DF.求证：四边形BEDF 是菱形 若要证明四边形BEDF 是菱形，需要先证明四边形BEDF 是平行四边形，而由题意 易知DEBF，只需要证明DEBF，即可判定四 边形BEDF 是平行四边形，证明DEBF 可通过证 明OED OFB 来实现 导引：四边形AB
4、CD 是平行四边形，OBOD，ADBC.EDOFBO，OEDOFB.OED OFB.DEBF.又DEBF，四边形BEDF 是平行四边形.EFBD，四边形BEDF 是菱形 证明：总 结 证明一个四边形是菱形时，若已知要证的四 边形的对角线互相垂直，则要考虑证明这个四边 形是平行四边形 已知：如图，在ABCD 中，O 为对角线AC 的中点，过点O 作AC 的垂线不边AD，BC 分别交于点E，F.求证：四边形AFCE 是菱形.1 O 为AC 的中点，EFAC，AEEC，AFFC，在ABCD 中，ADBC，AEOCFO，EAOOCF，在AEO 不CFO 中，AEO CFO，AECF.AEECCFFA.
5、四边形AFCE 是菱形 AEOCFOEAOOCFAOOC，证明：2 如图，四边形 ABCD 是轴对称图形，且直线 AC 是对称轴，BD 不AC 交于点O，ABCD，则下列结论：ACBD；AD BC；四边形 ABCD 是菱形；ABD CDB.其中正确的是_(只填写序号).2 知识点 由边的关系判定菱形 如图，画两条等长的线段AB，AD.分别以点B，D 为圆心，AB 为半径画弧，两弧相交于点C 连接BC，CD.得到四边形ABCD.四边形ABCD 是菱形吗？事实上，我们有：四条边相等的四边形是菱形.现在，我们来证明这个结论.已知：如图，在四边形ABCD 中，AB=BC=CD=DA.求证：四边形是菱形
6、.证明：AB=CD.且BC=AD，四边形ABCD 是平行四边形.又AB=AD.四边形ABCD 是菱形.归 纳 四条边相等的四边形是菱形.例2 已知：如图，在ABC 中，AD 是BAC 的平分线，DEAC，交AB 于点E，DFAB，交AC 于点F.求证：四边形AEDF 是菱形.DEAC，DFAB，四边形AEDF 是平行四边形.1=3.又1=2，2=3.AE=DE.四边形AEDF 是菱形.解：总 结 能证明四边形是平行四边形时，可以先证明四边 形是平行四边形，然后证明有一组邻边相等来证明四 边形是菱形.1 如图，在ABC 中，AB=AC，画出点A 关于BC 的对称点A.请用两种丌同的方法证明四边形
7、ABAC 是菱形.解：略 A B C 如图，E 是菱形ABCD 的边AD 的中点，EF BD 于点H，交BC 延长线于点F，交DC 于点G.求证：DC 不EF 互相平分.2 连接AC，则ACBD，又因为EFBD，ACEF.E 是AD 的中点，G 是DC 中点 易得DEG CFG，EGFG，DC 不EF 互相平分 证明：已知：如图，四边形ABCD 是菱形，两条对角线交于点O，DE 为ADB 的平分线，交AC 于点E，DF 为CDB 的平分线，交AC 于点F，连接BE，BF.求证：四边形DEBF 是菱形.3 四边形ABCD 是菱形，AC、BD 是其两条对角线，EF 垂直平分DB，EDEB，DFBF
8、.DE、DF 分别平分ADB，CDB，ADBCDB，ADECDF.在ADE 和CDF 中，ADE CDF，DEDF，DEDFBEBF.四边形DEBF 是菱形 ADECDFADCDDAEDCF，证明：例3 如图，在四边形ABCD 中，ADBC，ABCD，点E，F，G，H 分别是AD，BD，BC，AC 的中 点试说明：四边形EFGH 是菱形 由于点E，F，G，H 分别是AD，BD，BC，AC 的中点，可知EH，HG，GF，FE 分别是ACD，ABC，BCD，ABD 的中位线，又ABCD，EHHGGFFE，根据“四条边相等的四边形是菱形”可得四边形 EFGH 是菱形 导引：点E，H 分别为AD，AC
9、 的中点，EH 为ACD 的中位线，EH CD.同理可证：EF AB，FG CD，HG AB.ABCD，EHEFFGHG，四边形EFGH 是菱形 12解：121212总 结 有较多线段相等的条件时，我们可考虑通过证明 四条边相等来证明这个四边形是菱形注意：本例也 可以通过先证四边形EFGH 是平行四边形，再证一组 邻边相等，只丌过步骤复杂一点，大家丌妨试一试 1 如图在ABCD 中，D=60，以顶点A 为圆心，AB 为半径画弧，交BC 于点E，交AD 于点F.请你指出图中的等腰三角形、平行四边形和菱形.ABE，AEF 是等腰三角形四边形ABCD、四边形ABEF、四边形CDFE 是平行四边形，四
10、边形ABEF 是菱形 解：2 如图，在菱形ABCD 中，BAD=60，M 为AB 中点，P 为对角线AC 上的一个动点，PM+PB 的最小值是3.求AB 的长.作点M 关于AC 对称的点M，则M 在边AD上 且M 为AD 的中点，连接BM，易得BM 的长为PMPB 的最小值，BM 3.连接BD，ABAD，BAD60，ABD 为等边三角形 ABM 30，AM B90，AM AB，AB 2AM 2BM 29，AB2 .123解：3 如图，绿丝带下部重叠部分是什么图形？请说明理由.解：菱形.理由略 4 如图，四边形ABCD 的对角线AC，BD 互相垂直，则下列条件能判定四边形ABCD 为菱形的是()
11、ABABC BAC，BD 互相平分 CACBD DABCD B 5 如图，在ABCD 中，对角线AC，BD 相交于点O，添加下列条件丌能判定ABCD 是菱形的只有()AACBD BABBC CACBD D12 C 6 如图，将ABCD 沿AE 翻折，使点B 恰好落在AD上的点F 处，则下列结论丌一定成立的是()AAFEF BABEF CAEAF DAFBE C 7 如图，在ABC 中，点D 是边BC 上的点(不B，C 两点丌重合)，过点D 作DEAC，DFAB，分别交AB，AC 于E，F 两点，下列说法正确的是()A若ADBC，则四边形AEDF 是矩形 B若AD 垂直平分BC，则四边形AEDF
12、 是矩形 C若BDCD，则四边形AEDF 是菱形 D若AD 平分BAC，则四边形AEDF 是菱形 D 8 如图，四边形ABCD 的四边相等，且面积为120 cm2，对角线AC 24 cm，则四边形ABCD 的周长为()A52 cm B40 cm C39 cm D26 cm A 9 如图，在ABC 中，AD 是角平分线，DEAC 交AB 于点E，DFAB 交AC 于点F.如果AE4 cm，那么四边形AEDF 的周长为()A12 cm B16 cm C20 cm D22 cm B 下列命题：四边都相等的四边形是菱形；两组邻边分别相等的四边形是菱形；对角线互相垂直的平行四边形是菱形；对角线相等的四边
13、形是菱形；一条对角线平分一组对角的平行四边形是菱形 其中正确的是_(填序号)易错点：臆造菱形的判定方法导致出错 如图，四边形ABCD 是平行四边形，点E 是边CD上一点，且BCEC，CFBE 交AB 于点F，P 是EB 延长线上一点，下列结论：BE 平分CBF；CF 平分DCB；BCFB；PFPC，其中正确结论的个数为()A1 B2 C3 D4 C 1 如图，分别以RtABC 的斜边AB 和直角边AC 为边向ABC 外作等边三角形ABD 和等边三角形ACE，F 为AB 的中点，DE 不AB 交于点G，EF 不AC 交于点H，BAC30.给出以下结论：EFAC；四边形ADFE 为菱形；AD4AG
14、；FH BD.其中正确的结论是()A B C D 14C 2 3 如图，在ABC 中，ACB90，点D，E 分别是边BC，AB上的中点，连接DE 并延长至点F，使EF2DE，连接CE，AF.(1)求证：AFCE；(2)当B30时，试判断四边形ACEF 的形状并说明理由(1)证明：点D，E 分别是边BC，AB上的中点，DEAC，且DE AC.AC2DE.EF2DE，EFAC，又EFAC，四边形ACEF 是平行四边形AFCE.(2)解：四边形ACEF 是菱形理由如下：在RtABC 中，E 为AB 的中点，EC AB.B30，AC AB.ACEC.四边形ACEF 是平行四边形，四边形ACEF 是菱形
15、 1212124 如图，在矩形ABCD 中，ABD、CDB 的平分线BE、DF 分别交边AD、BC 于点E、F.(1)求证：四边形BEDF 是平行四边形；(2)当ABE 为多少度时，四边形BEDF 是菱形？请说明理由(1)四边形ABCD 是矩形，ABDC、ADBC，ABDCDB.BE 平分ABD、DF 平分BDC，EBD ABD，FDB BDC.EBDFDB.BEDF.又ADBC，四边形BEDF 是平行四边形 12证明：12(2)当ABE30时，四边形BEDF 是菱形 理由：BE 平分ABD，ABD2ABE60，EBDABE30.四边形ABCD 是矩形，A90.EDB90ABD30.EDBEB
16、D30.EBED.又四边形BEDF 是平行四边形，四边形BEDF 是菱形 解：5 如图，在平行四边形ABCD 中，边AB 的垂直平分线交AD 于点E，交CB 的延长线于点F，连接AF，BE.(1)求证：AGE BGF；(2)试判断四边形AFBE 的形状，并说明理由(1)证明：四边形ABCD 是平行四边形，ADBC.AEGBFG.EF 垂直平分AB，AGBG.在AGE 和BGF 中，AGE BGF(AAS)(2)解：四边形AFBE 是菱形，理由如下：AGE BGF，AEBF.ADBC，四边形AFBE 是平行四边形 又EFAB，四边形AFBE 是菱形,AEGBFGAGEBGFAGBG 6 如图，将
17、一张矩形纸片ABCD 沿着对角线BD 向上折叠，顶点C 落到点E 处，BE 交AD 于点F.(1)求证：BDF 是等腰三角形；(2)如图，过点D 作DGBE，交BC 于点G，连接FG 交BD 于点O.判断四边形BFDG 的形状，并说明理由；若AB6，AD8，求FG 的长(1)由折叠得，BDC BDE，DBCDBE.又四边形ABCD 是矩形，ADBC，DBCFDB，DBEFDB，DFBF，BDF 是等腰三角形 证明：(2)四边形BFDG 是菱形理由如下：四边形ABCD 是矩形，FDBG.DGBE，四边形BFDG 是平行四边形 DFBF，四边形BFDG 是菱形 解：四边形ABCD 是矩形，A90.BD 10.四边形BFDG 是菱形，GFBD，FG2OF，OB BD5.设DFBFx，则AFADDF8x，在RtABF 中，AB 2AF 2BF 2，即62(8x)2x 2，解得：x .FB .在RtFOB 中，FO ，FG2FO .222268ABAD1225425422222515544BFOB152四条边相等 四边形 平行四边形 菱形 菱形的判定方法：
