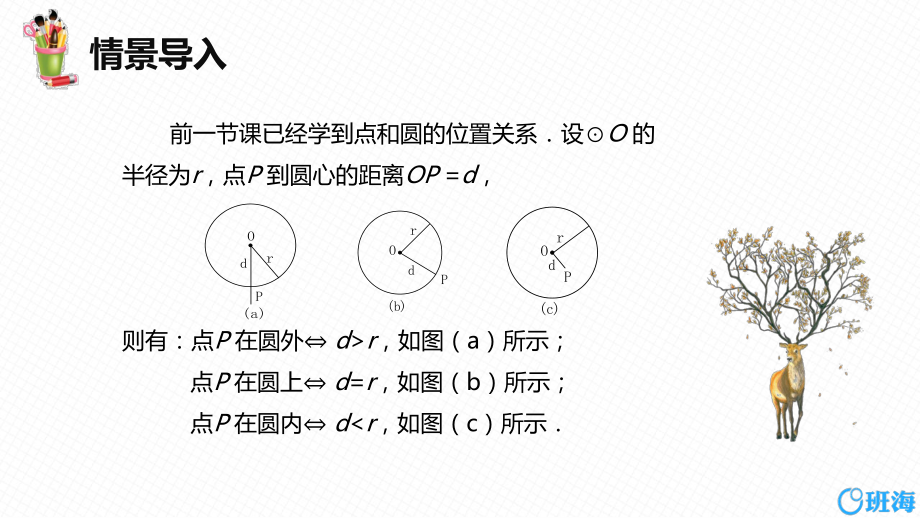
1、6 直线和圆的位置关系 第2课时 前一节课已经学到点和圆的位置关系设O 的 半径为r，点P 到圆心的距离OP=d，则有：点P 在圆外 dr，如图（a）所示；点P 在圆上 d=r，如图（b）所示；点P 在圆内 dr，如图（c）所示(a)rdPO(b)rdPO(c)rdPO1 知识点 切线的性质定理 前面我们已学过的切线的性质有哪些？答：切线和圆有且只有一个公共点；切线和圆心的距离等于半径.切线还有什么性质？切线的性质定理：圆的切线垂直于过切点的半径.例1 如图，AB 是O 的弦，AC 是O 的切线，A 为切点 BC 经过圆心若B20，则C 的大小为()A20 B25 C40 D50 D 如图，连
2、接OA，根据切线的性质，先求出OAC90，再根据等腰三角形的性质和B20，可以求出AOC40，最后根据直角三角形中两锐角互余就可以求出C50.答案：D 导引：总 结(1)半径处处相等可得等腰三角形，从而底角相等；(2)切线垂直于过切点的半径得直角三角形，从而两锐角互余 下列说法正确的是()A圆的切线垂直于半径 B垂直于切线的直线经过圆心 C经过圆心且垂直于切线的直线经过切点 D经过切点的直线经过圆心 1 C 如图，直线l 是O 的切线，A 为切点，B 为直线l 上一点，连接OB 交O 于点C.若AB12，OA5，则BC 的长为()A5 B6 C7 D8 2 D 如图，AB 是O 的直径，AC
3、切O 于点A，BC 交O 于点D，若C70，则AOD 的度数为()A70 B35 C20 D40 3 D 如图，O 是RtABC 的外接圆，ACB90，A25，过点C 作O 的切线，交AB 的延长线于点D，则D 的度数是()A25 B40 C50 D65 4 B 2 知识点 切线性质定理的应用 例2 如图，ABC 内接于O，AB 是O 的直径，BAC2B，O 的切线AP 与OC 的延长线 相交于点P，若PA6 cm，求AC 的长 3根据AB 是O 的直径求出ACB90，再根据BAC2B 求出B30，BAC60，得出AOC 是等边三角形，得出AOC60，OAAC，在RtOAP 中，求出OA，即可
4、求出AC 的长 导引：AB 是O 的直径，ACB90.又BAC2B，B30，BAC60.又OAOC，AOC 是等边三角形，AOC60，ACOA.PA 是O 的切线，OAP90.在RtOAP 中，PA6 cm，AOP60，OA 6(cm)，ACOA6 cm.解：6 3tan603PA 3 如图，在ABC 中，AB1，AC ，点O 在AB 的延长线上，AC 切O 于点C.求：(1)O 的半径；(2)A 的度数 例3 连接OC，易得RtOAC，运用勾股定理求O 的半径在RtOAC 中，利用锐角三角函数求A 的度数 导引：3(1)连接OC.AC 切O于点C，OCAC，设O 的半径为r，则OCOBr.O
5、AOBAB1r.在RtOAC 中，OA2OC 2AC 2，即(1r)2r 2()2，解得r1.故O 的半径为1.(2)由(1)得OC1，OA2.在RtOAC 中，sin A ，A30.解：312OC=OA总 结 当圆中有切线和切点时，通常连接过切点的半径，则这条半径必与切线垂直，本例中作辅助线的方法，适用于同类条件下与圆有关的求值或证明题 如图，一枚直径为d 的硬币沿着直线滚动一圈，圆心经过的距离是多少？1 解：d.如图，以点O 为圆心的两个圆中，大圆的弦AB 切小圆于点C，OA 交小圆于点D，若OD2，tan OAB ，则AB 的长是()A4 B2 C8 D4 2 3312C 如图，菱形AB
6、CD 的边AB20，面积为320，BAD90，O 与边AB，AD 都相切，AO10，则O 的半径长等于()A5 B6 C2 D3 3 52C 如图，在平面直角坐标系中，点P 在第一象限内，x 轴与P 相切于点Q，y 轴与P 相交于M(0，2)，N(0，8)两点，则点P 的坐标是()A(5，3)B(3，5)C(5，4)D(4，5)4 D 如图，圆形薄铁片与直角三角尺、直尺紧靠在一起平放在桌面上已知铁片的圆心为O，三角尺的直角顶点C 落在直尺的10 cm处，铁片与直尺的唯一公共点A 落在直尺的14 cm处，铁片与三角尺的唯一公共点为B.下列说法错误的是()A圆形铁片的半径是4 cm B四边形AOB
7、C 为正方形 C弧AB 的长度为4 cm D扇形OAB 的面积是4 cm2 5 C 如图，ABC 中，AB5，BC3，AC4，以点C 为圆心的圆与AB 相切，则C 的半径为()A2.3 B2.4 C2.5 D2.6 易错点：忽视“过切点”这一条件而致错.B 如图，AB 是O 的直径，点C 为O 外一点，CA，CD 是O 的切线，A，D 为切点，连接BD，AD.若ACD30，则DBA 的大小是()A15 B30 C60 D75 1 B 如图，圆内接四边形ABCD 的边AB 过圆心O，过点C 的切线与边AD 所在直线垂直于点M，若ABC55，则ACD 等于()A20 B35 C40 D55 2 A
8、 3 如图，已知AB 是O 的直径，CD 与O 相切于C，BECO.(1)求证：BC 是ABE 的平分线；(2)若DC8，O 的半径OA6，求CE 的长 DE 是O 的切线，OCDE.BECO，OCBCBE.OCOB，OCBOBC.CBEOBC.BC 平分ABE.(1)证明：在RtCDO 中，DC8，OCOA6，OD OCBE，CE4.8.(2)解：22228610.CDOC.DCDOCEOB 810.6CE 4 如图，在ABC 中，ACBC，ACB90，O(圆心O 在ABC 内部)经过B，C 两点，交AB 于点E，过点E 作O 的切线交AC 于点F.延长CO 交AB 于点G，作EDAC 交C
9、G 于点D.(1)求证：四边形CDEF 是平行四边形；(2)若BC3，tanDEF2，求BG 的值 如图，连接CE.在ABC 中，ACBC，ACB90，B45.COE90.CEOECO45.EF 是O 的切线，FEO90.FEC45.FECECO.EFCG.又EDAC，四边形CDEF 是平行四边形 (1)证明：如图，过G 作GMBC于M，GMB 是等腰直角三角形，MBGM.四边形CDEF 是平行四边形，FCDFED.ACDGCBGCBCGM90，CGMACD.CGMDEF.tanDEF2，tanCGM CM2GM，又BCCMBM2GMGM3，GM1.BG GM (2)解：2.CMGM 2.25
10、 如图，AB 是O 的直径，BAC90，四边形EBOC 是平行四边形，EB 交O 于点D，连接CD 并延长交AB 的延长线于点F.(1)求证：CF 是O 的切线；(2)若F30，EB4，求图中阴影部分的面积(结果保留根号和)如图，连接OD.四边形EBOC 是平行四边形，OCBE.AOCOBE，CODODB.OBOD，OBDODB.DOCAOC.在COD 和COA 中，OCOC，CODCOA，ODOA，COD COA.(1)证明：CDOCAO90.圆心O 到CF 的距离等于O 的半径 CF 是O 的切线 F30，ODF90，DOF60，AOD120.ODOB，OBD 是等边三角形，BDODBO6
11、0，OBBD.易得EDCECD30，EDEC.四边形EBOC 是平行四边形，ECEDBODB.EB4，OBODOA2.(2)解：AOCCOD，AOC60.在RtAOC 中，OAC90，AOC60，OCA30.OA2，OC4.AC S阴影2SAOCS扇形OAD 222 3.OCOA 211422 2 3 24 3.233 6 已知AB 是O 的直径，AT 是O 的切线，ABT50，BT交O 于点C，E 是AB 上一点，延长CE 交O 于点D.(1)如图，求T 和CDB 的大小；(2)如图，当BEBC 时，求CDO 的大小(1)如图，连接AC，AT 是O 的切线，AB 是O 的直径，TAB90.ABT50，T90ABT40.由AB 是O 的直径，得ACB90.CAB90ABC40.CDBCAB40.解：(2)如图，连接AD，在BCE 中，BEBC，EBC50，BCEBEC65.BADBCD65.OAOD，ODAOAD65.ADCABC50，CDOODAADC655015.圆的切线垂直于过切点的半径.已知直线满足：(1)过圆心；(2)过切点；(3)垂直于直线任意两个，就可得到第三个.
