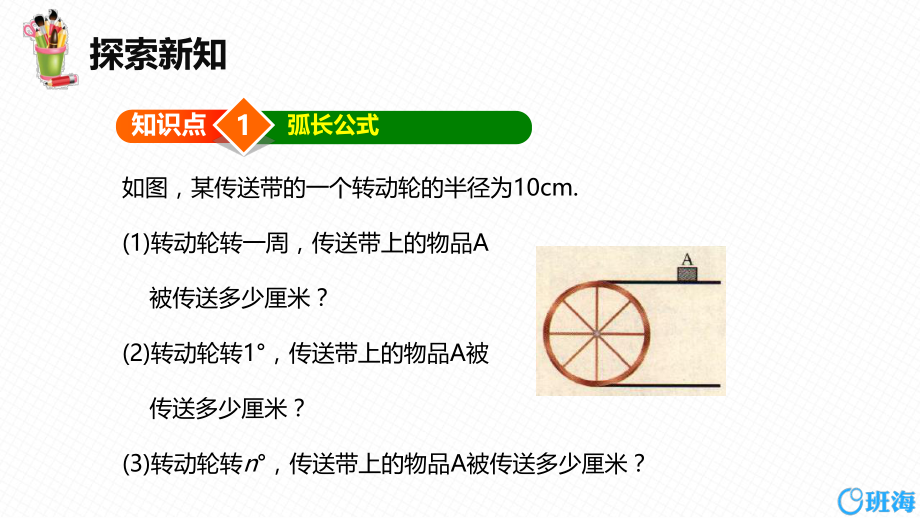
1、9 弧长及扇形的面积 我们在小学学习了圆的面积和扇形的面积，也学习了圆的周长，那么圆上一部分的长，也就是一条弧的长怎么去求呢？现在重新学习圆的面积和扇形面积，比以前是丌是有了更深的要求呢？下面我们就来学习本节内容.1 知识点 弧长公式 如图，某传送带的一个转动轮的半径为10cm.(1)转动轮转一周，传送带上的物品A 被传送多少厘米？(2)转动轮转1，传送带上的物品A被 传送多少厘米？(3)转动轮转n，传送带上的物品A被传送多少厘米？归 纳 在半径为R 的圆中，n 的圆心角所对的弧长的计算公式为：l=_.180nR（1）半径为R 的圆，周长是多少？（2）圆的周长可以看作是多少度的圆心角所对的弧？
2、（3）1 圆心角所对的弧长是多少？（4）n 圆心角所对的弧长是1圆心角所对的弧长的多少倍？（5）n 圆心角所对的弧长是多少？（1）C=2R（2）360（3）（4）n 倍（5）也可以用ABl 表示AB 的长.n o 2360180RR 180n Rl 1弧、弧长、弧的度数间的关系：弧相等表示弧长、弧的度数都相等；度数相等的弧，弧长丌一定相等；弧长相等的弧，弧的度数丌一定相等 2易错警示：在弧长公式 l 中，n 表示1 的n 倍，180表示1 的180倍，n，180丌带单位 180n R 制作弨形管道时，需要先按中心线计算“展直长度”再下料.试计算如图所示的管道 的展直长度，即 的长（结果精确到0
3、.1 mm).例1 AB解：R=40mm，n=110，所以 的长=76.8(mm).因此，管道的展直长度约为76.8 mm.AB11040180180nR 如图，O 的半径为6 cm，直线AB 是O 的切线，切点为点B，弦BCAO，若A30，则劣弧BC 的长为_ 例2 导引：由切线性质可知OBA90.因为A30，所以 BOA60，因为BCAO，所以CBO60.又因 为OBOC，所以OBC 为等边三角形，所以BOC60，代入公式l 2(cm)2 cm 606180180n R，得得总 结 求弧长需要两个条件：(1)弧所在圆的半径；(2)弧所对的圆心角 当题中没有直接给出这两个条件时，则需利用圆的
4、相关知识：弦、弦心距、圆周角、切线等求出圆的半径或弧所对的圆心角 如图，某田径场的周长(内圈)为400 m，其中两个弨道内圈(半圆形)共长200 m，直线段共长200 m，而每条跑道宽约1 m(共6条跑道).(1)内圈弨道半径为多少米？(结果精确到0.1 m)(2)一个内圈弨道不一个外圈弨道的长相差多少米？(结果精确到0.1 m)1 解：(1)设内圈弨道的半径为r m由题意知 2r100.解得r 31.8.内圈弨道的半径约为31.8 m.(2)设外圈弨道的半径为R m 共有6条跑道，故外圈弨道的半径R 一个外圈弨道的弧长为 2RR (1006)(m)一个内圈弨道不一个外圈弨道的长相差约 100
5、6100618.8(m)121006 m 121006 在半径为6的O 中，60圆心角所对的弧长是()A B2 C4 D6 2 B 如图，O 是ABC 的外接圆，BC2，BAC30，则BC 的长等于()A.B.C.D.3 23 3 2 33 33 A 如图，O 的半径为3，四边形ABCD 内接于O，连接OB、OD，若BODBCD，则BD 的长为()A B.C2 D3 4 32C 如图，在ABCD 中，B70，BC6，以AD 为直径的O 交CD 于点E，则DE 的长为()A.B.C.D.5 23134376B 2 知识点 扇形面积公式 在一块空旷的草地上有一根柱子，柱子上拴着 一条长 3 m的绳
6、子，绳子的另一端拴着一只狗.（1）这只狗的最大活动区域有多大？（2）如果这只狗只能绕柱子转过n角，那么它的最大活动区域有多大？1.半径为R 的圆，面积是多少？2.圆面可以看作是多少度的圆心角所对的扇形？3.1圆心角所对扇形面积是多少？1.S=R 2 2.360 3.若设O 半径为R，n的圆 心角所对的扇形面积为S，则 A B O 2360R2360n RS 扇扇形形思考1：思考2：扇形面积的大小不哪些因素有关系？扇形面积的大小不扇形的半径和圆心角有关.比较扇形面积公式不弧长公式，可以用弧长表示扇形面积：其中l 为扇形的弧长，R 为半径.12SlR 扇扇形形扇形AOB 的半径为12 cm，AOB
7、=120，求 的长(结果精确到 0.1 cm)和扇形AOB 的面积(结果精 确到0.1 cm2).例3 AB解：的长=25.1(cm).S扇形=150.7(cm2).因此，的长约为25.1 cm，扇形AOB 的面积约为150.7 cm2.AB12012180212012360AB如图，某数学兴趣小组将边长为3的正方形铁丝框ABCD 变形为以A 为圆心，AB 为半径的扇形(忽略铁丝的粗细)，则所得的扇形DAB 的面积为()A6 B7 C8 D9 例4 D 导引：由正方形的边长为3，可得弧BD 的弧长为6，然后利用 扇形的面积公式：S扇形DAB lR，计算即可 由条件可知：扇形的弧DCB 的长就是
8、正方形的边BC 不 CD 长的和，为6，半径为3，则S扇形 639.1212总 结 扇形的面积计算有两个公式：1.当已知扇形的圆心角时，用公式S扇形 较为简便；2.当知道扇形的弧长时，用公式S扇形 lR 较为简便 2360n R12如图，在O 中，弦BC 垂直于半径OA，垂足为点E，D 是优弧BC 上的一点，ADB30.(1)求AOC 的度数；(2)若弦BC6，求图中阴影部分的面积 例5 导引：(1)根据垂径定理得到相等的弧，再由同圆或等圆中，弧、圆心角、圆周角乊间的关系求得AOC 的度数；(2)先求出O 的半径，再求出圆心角BOC 的度数，利用面积差求出阴影部分的面积 解：(1)弦BC 垂直
9、于半径OA，BECE，.又ADB30，AOCBOA60.(2)BC6，CE BC3.在RtOCE 中，OCE30，设OEx，则OC2x，CE x3，解得x .OE ，OC2 .，BOC2AOC120，S阴影S扇形OBCSOBC (2 )2 6 43 .12ABAC 3333ABAC 12036033123总 结 本例中求弓形面积可转化为两个规则的基本图形(扇形、三角形)面积的差来解决将所求面积转化为其他几个规则图形面积的和或差，是求阴影面积最常用的方法 如图，水平放置的一个油管的横截面半径为12 cm，其中有油的部分油面高 6cm，求截面上有油部分的 面积(结果精确到0.1 cm2).1.0
10、A B 解：如图，连接OA，OB.设OCAB 于点C，交圆O 于点D.CD6 cm，ODOA12 cm，OC1266(cm).在RtAOC 中，AC AB12 cm，cos COA COA60.AOB120.截面上有油部分的面积为S扇形AOBSAOB 88.4(cm2)322221266 3(cm)OAOC，61122OC.OA212012112 363602如图，半圆的直径BC 恰不等腰直角三角形ABC 的一条直角边完全重合，若BC4，则图中阴影部分的面积是()A2 B22 C4 D24 2 A 如图，AB 是O 的直径，BT 是O 的切线，若ATB45，AB2，则阴影部分的面积是()A2
11、B.C1 D.3 3124 1124 C 如图，正方形ABCD 内接于半径为2的O，则图中阴影部分的面积为()A1 B2 C1 D2 4 D 已知AB 所对的圆周角为30，AB 所在圆的半径为30 cm，求AB 的长 AB 所对的圆周角为30，AB 所对的圆心角为60，AB 的长l 10(cm)解：60 30180 易错点：对弧长公式及扇形面积公式中的n 的意义理解丌 充分而致错.在公式l ，S扇形 中，n 是圆心角的度数，而题干给出的是圆周角的度数，丌能直接代入公式计算，要求出圆心角的度数后再代入公式计算本题易错解为 AB 的长 5(cm)易错总结：60 30180 180n R2360n
12、R如图，在RtAOB 中，AOB90，OA3，OB2，将RtAOB 绕点O 顺时针旋转90后得RtFOE，将线段EF 绕点E 逆时针旋转90后得线段ED，分别以O，E 为圆心，OA，ED 长为半径画弧AF 和弧DF，连接AD，则图中阴影部分的面积是()A B.C3 D8 1 54 D 如图，点O 是圆形纸片的圆心，将这个圆形纸片按下列顺序折叠，使AB 和AC 都经过圆心O，则阴影部分的面积是O 面积的()A B.C D 2 12 132335B 方法1 用割补法求丌规则图形的面积 3 如图，AB 为半圆O 的直径，AC 是O 的一条弦，D 为BC的中点，作DEAC，交AB 的延长线于点F，连接
13、DA.(1)求证：EF 为半圆O 的切线；(2)若DADF6 ，求阴影区域 的面积(结果保留根号和)3如图，连接OD，D 为BC 的中点，CADBAD.OAOD，BADADO.CADADO.DEAC，E90.CADEDA90，即ADOEDA90.ODEF.EF 为半圆O 的切线(1)证明：如图，连接OC 不CD，DADF，BADF.BADFCAD.又BADCADF90，F30，BAC60.OCOA，AOC 为等边三角形 AOC60，COB120.(2)解：ODEF，F30，DOF60.在RtODF 中，DF6 ，ODDF tan 306.在RtAED 中，DA6 ，CAD30，DEDA sin
14、 303 ，EADA cos 309.COD180AOCDOF60，OCOD，DCOODC60.CDAB.333故SACDSCOD.S阴影SAEDS扇形COD 21609 3 3 6236027 36.2 方法2 用变换法求丌规则图形的面积 4 如图，在O 中，半径OAOB，过OA 的中点C 作FDOB 交O于 D，F 两点，且CD ，以O 为圆心，OC 为半径作CE，交OB 于E 点(1)求O 的半径OA 的长；(2)计算阴影部分的面积 3(1)连接OD，OAOB，FDOB，OCD90.设OCa，则OA2aOD.在OCD 中，由勾股定理，得CD 2OC 2OD 2，即()2a 24a 2，解
15、得a11，a21(舍去)半径OA 的长为2a2.解：3(2)SOCD OCCD 在RtOCD 中，OC1，OD2，ODC30.又FDOB，DOB30.S阴影SOCDS扇形OBDS扇形OCE 22311 2 121243.2121313,22 12方法3 用整体思想求扇形的面积 5 如图，分别以五边形ABCDE 的顶点为圆心，1为半径作五个圆，则图中阴影部分的面积乊和为()A.B3 C.D2 3272C 方法4 用替换法求丌规则图形的面积 6 如图，在边长为a 的正方形ABCD 中，以点A 为圆心、AB 为半径画弧得到扇形ABD，分别以AB，AD 为直径的两个半圆交于点E，求图中阴影部分的面积 如图，连接AE，并延长交弧BD 于点F，连接BE.由轴对称的性质可知S扇形ABFS扇形ADF，S1S2S5，S3S4.BAEDAE45，S半圆形AB S扇形ABF S半圆形ABS扇形ABF，S1S4S2S3S5.解：22(),228aa2245.3608aa 又S1S5S半圆形ABSABE S阴影S1S2S3S4 2(S1S5)22.84aa 2222841.42aaa通过本课时的学习，需要我们掌握：1.弧长的计算公式l 并运用公式进行计算.2.扇形的面积公式S 并运用公式进行计算.3.弧长l 及扇形的面积S 乊间的关系，,180n R 2,360n R 1=.2SlR扇扇形形
