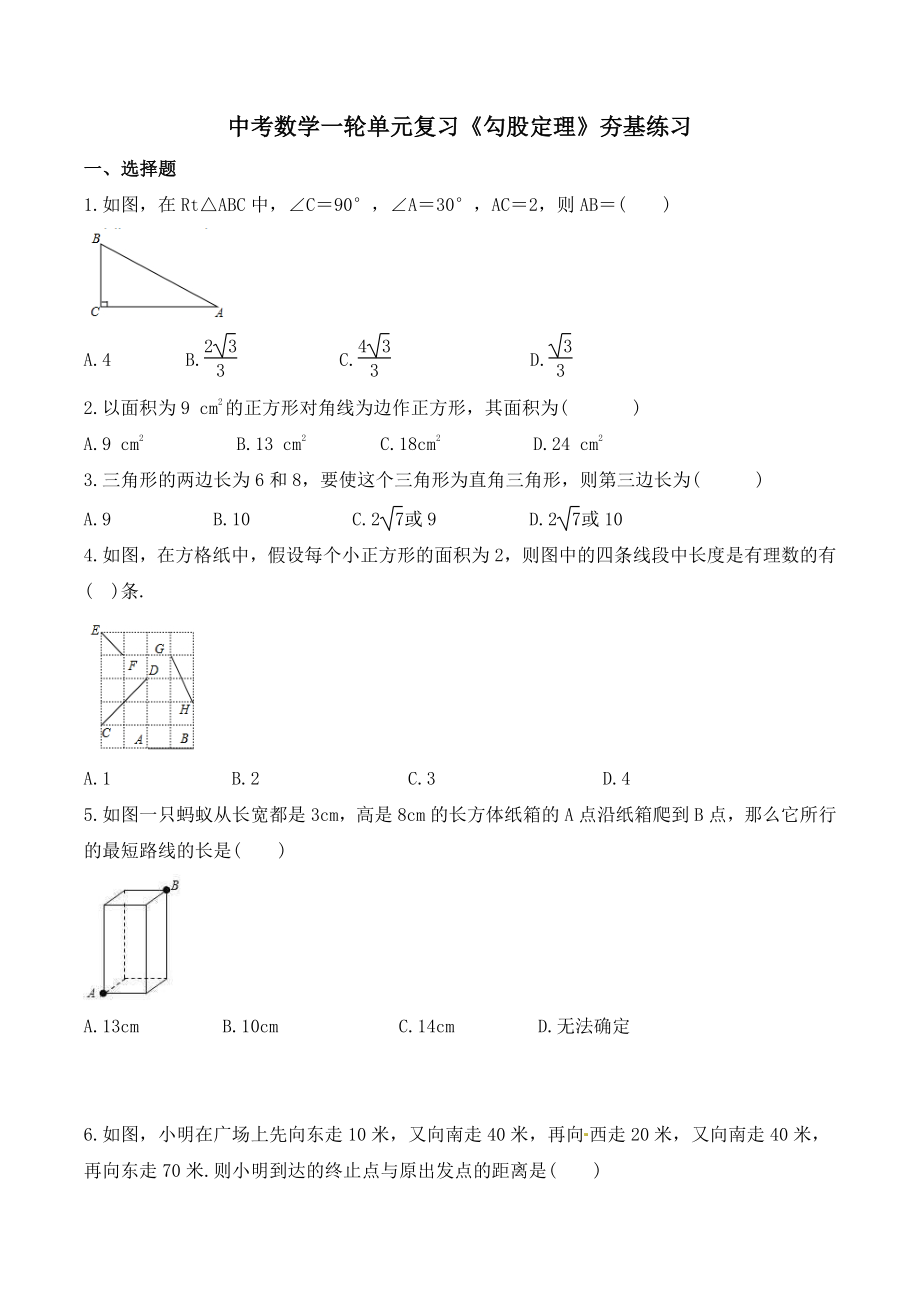
1、 中考数学一轮单元复习勾股定理夯基练习中考数学一轮单元复习勾股定理夯基练习 一一、选择题、选择题 1.如图，在 RtABC 中，C90，A30，AC2，则 AB( ) A.4 B.2 33 C.4 33 D.33 2.以面积为 9 cm2的正方形对角线为边作正方形，其面积为( ) A.9 cm2 B.13 cm2 C.18cm2 D.24 cm2 3.三角形的两边长为 6 和 8，要使这个三角形为直角三角形，则第三边长为( ) A.9 B.10 C.2 7或 9 D.2 7或 10 4.如图，在方格纸中，假设每个小正方形的面积为 2，则图中的四条线段中长度是有理数的有( )条. A.1 B.2
2、 C.3 D.4 5.如图一只蚂蚁从长宽都是 3cm，高是 8cm 的长方体纸箱的 A 点沿纸箱爬到 B 点，那么它所行的最短路线的长是( ) A.13cm B.10cm C.14cm D.无法确定 6.如图，小明在广场上先向东走 10 米，又向南走 40 米，再向 西走 20 米，又向南走 40 米，再向东走 70 米.则小明到达的终止点与原出发点的距离是( ) A.90 米 B.100 米 C.120 米 D.150 米 7.三角形的三边长 a，b，c 满足 2ab(ab)2c2，则此三角形是( ) A.钝角三角形 B.锐角三角形 C.直角三角形 D.等边三角形 8.在ABC 中，A、B、
3、C 的对边分别是 a、b、c，下列判断错误的是( ) A.如果CBA，则ABC 是直角三角形 B.如果 a2c2b2，则ABC 不是直角三角形 C.如果(ca)(ca)b2，则ABC 是直角三角形 D.如果ABC523，则ABC 是直角三角形 9.如图，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆 8 m 处，发现此时绳子末端距离地面 2 m，则旗杆的高度为(滑轮上方的部分忽略不计)( ) A.12 m B.13 m C.16 m D.17 m 10.如图，A，B 两个村庄分别在两条公路 MN 和 EF 的边上，且 MNEF，某施工队在 A，B，C三个村之间
4、修了三条笔直的路.若MAB65，CBE25，AB160km，BC120km，则 A，C 两村之间的距离为( ) A.250km B.240km C.200km D.180km 11.如图，ABC 的顶点 A、B、C 在边长为 1 的正方形网格的格点上，BDAC 于点 D.则 BD 的长为( ) A.235 B.345 C.455 D.355 12.如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD、 正方形EFGH、 正方形MNKT的面积分别为S1、 S2、 S3.若S1S2S315， 则S2的值是( ) A.3 B.154 C.5 D.152 二二、填空题
5、、填空题 13.若三角形三边之比为 3：4：5，周长为 24，则三角形面积 14.古希腊的哲学家柏拉图曾指出，如果 m 表示大于 1 的整数，a2m，bm21，cm21，那么 a，b，c 为勾股数.请你利用这个结论得出一组勾股数是 . 15.已知a、 b、 c是ABC三边长， 且满足关系式|ab|0， 则ABC形状为 16.已知正方形、 在直线上， 正方形如图放置， 若正方形、 的面积分别 4cm2和 15cm2，则正方形的面积为 17.如图，正方形的边长是 1 个单位长度，则图中 B 点所表示的数是 ；若点 C 是数轴上一点，且点 C 到 A 点的距离与点 C 到原点的距离相等，则点 C 所
6、表示的数是 . 18.如图，ABC 中，ABAC13，BC10，ADBC，BEAC，P 为 AD 上一动点，则 PEPC的最小值为 . 三三、解答题、解答题 19.如图，在ABC 中，CD 是 AB 边上高，若 AD16，CD12，BD9 (1)求ABC 的周长 (2)判断ABC 的形状并加以证明 20.阅读下列解题过程： 已知a，b，c为ABC的三边长，且满足a2c2b2c2a4b4，试判断ABC的形状 解：因为a2c2b2c2a4b4， 所以c2(a2b2)(a2b2)(a2b2) 所以c2a2b2 所以ABC是直角三角形. 回答下列问题： (1)上述解题过程，从哪一步开始出现错误?该步的
7、序号为 . (2)错误的原因为 . (3)请你将正确的解答过程写下来. 21.某菜农要修建一个塑料大棚，如图所示，若棚宽 a4m，高 b3m，长 d40m。求覆盖在顶上(如右图阴影部分)的逆料薄膜的面积。 22.去年某省将地处A，B两地的两所大学合并成了一所综合性大学，为了方便A，B两地师生的交往，学校准备在相距(1 3)km的A，B两地之间修筑一条笔直公路(即图中的线段AB)，经测量，在A地的北偏东 600方向、B地的西偏北 450方向的C处有一个半径为 0.7km的公园，问计划修筑的这条公路会不会穿过公园？为什么？ 23.如图，这是一个供滑板爱好者使用的U型池，该U型池可以看作是一个长方体
8、去掉一个“半圆柱”而成，中间可供滑行部分的截面是半径为 4m的半圆，其边缘ABCD20m，点E在CD上，CE2m，一滑行爱好者从A点到E点，则他滑行的最短距离是多少？(边缘部分的厚度可以忽略不计，结果取整数) 24.如图，在ABC 中，ADBC 于 D，BDAD，DGDC，E，F 分别是 BG，AC 的中点 (1)求证：DEDF，DEDF； (2)连接 EF，若 AC10，求 EF 的长 25.如图，在等腰直角三角形ABC中，ABC90，D为AC边中点，过D点做DEDF，交AB于E，交BC于F若AE4，FC3，求EF长. 参考答案参考答案 1.C 2.C. 3.D 4.B 5.B. 6.B.
9、7.C. 8.B. 9.D. 10.C. 11.C. 12.C 13.答案为：24. 14.答案为：4，3，5(答案不唯一). 15.答案为：等腰直角三角形. 16.答案为：19 17.答案为： 2；22. 18.答案为：. 19.解：(1)CD 是 AB 边上高， CDACDB90， AC20，BC15， ABADBD25， ABC 的周长ABBCAC25201560； (2)ABC 是直角三角形，理由如下：202152252， 即 AC2BC2AB2， ABC 是直角三角形 20.解：(1) (2)忽略了a2b20 的可能 (3)解：因为a2c2b2c2a4b4， 所以c2(a2b2)(a
10、2b2)(a2b2)， 所以ab或c2a2b2 所以ABC是等腰三角形或直角三角形. 21.解：根据勾股定理，得直角三角形的斜边为 5m， 再根据矩形的面积公式，得：540200m2 22.解：如图所示，过点 C 作 CDAB，垂足为点 D 由题意可得 CAB300，CBA450 在 RtCDB 中，BCD45 ， CBABCD，BDCD 在 RtACD 中，CAB30 ， AC2CD 设 CDDBx，则 AC2x 由勾股定理，得 AD2AC2CD2AD 3x ADDBAB， 3xx1 3，解得x1 因为 CD10.7，所以计划修筑的这条公路不会穿过公园 23.解：将半圆面展开可得： AD4米
11、，DEDCCEABCE18 米， 在RtADE中，AE22 米 即滑行的最短距离约为 22 米 24.证明：(1)ADBC， ADBADC90， 在BDG 和ADC 中， BDADBDGADCDGDC， BDGADC(SAS)， BGAC，BGDC， ADBADC90，E，F 分别是 BG，AC 的中点， DE12BGEG，DF12ACAF， DEDF，EDGEGD，FDAFAD， EDGFDA90， DEDF； (2)解：AC10， DEDF5， 由勾股定理得，EF DE2DF25 2. 25.解：连接 BD D 是 AC 中点， ABDCBD45，BDADCD，BDAC EDB+FDB90，FDB+CDF90， EDBCDF， 在BED 和CFD 中， EBDC,BDCD,EDBCDF， BEDCFD(ASA)， BECF； ABBC，BECF3， AEBF4， 在 RtBEF 中，EF 5.
