1、 河南省安阳市五校联考河南省安阳市五校联考 2020-2021 学年九年级上数学期中试卷学年九年级上数学期中试卷 一选择题（共一选择题（共 10 小题）小题） 1下列防控疫情的图标中，既是轴对称图形，又是中心对称图形的是（ ） A B C D 2若关于 x 的一元二次方程（a+1）x2+x+a210 的一个根是 0，则 a 的值为（ ） A1 B1 C1 或1 D 3如图，AB 是O 的弦，点 C 在圆上，已知AOB100，则C（ ） A40 B50 C60 D80 4 定义运算： mnmn2mn1 例如： 424224217 则方程 1x0 的根的情况为 （ ） A有两个不相等的实数根 B有
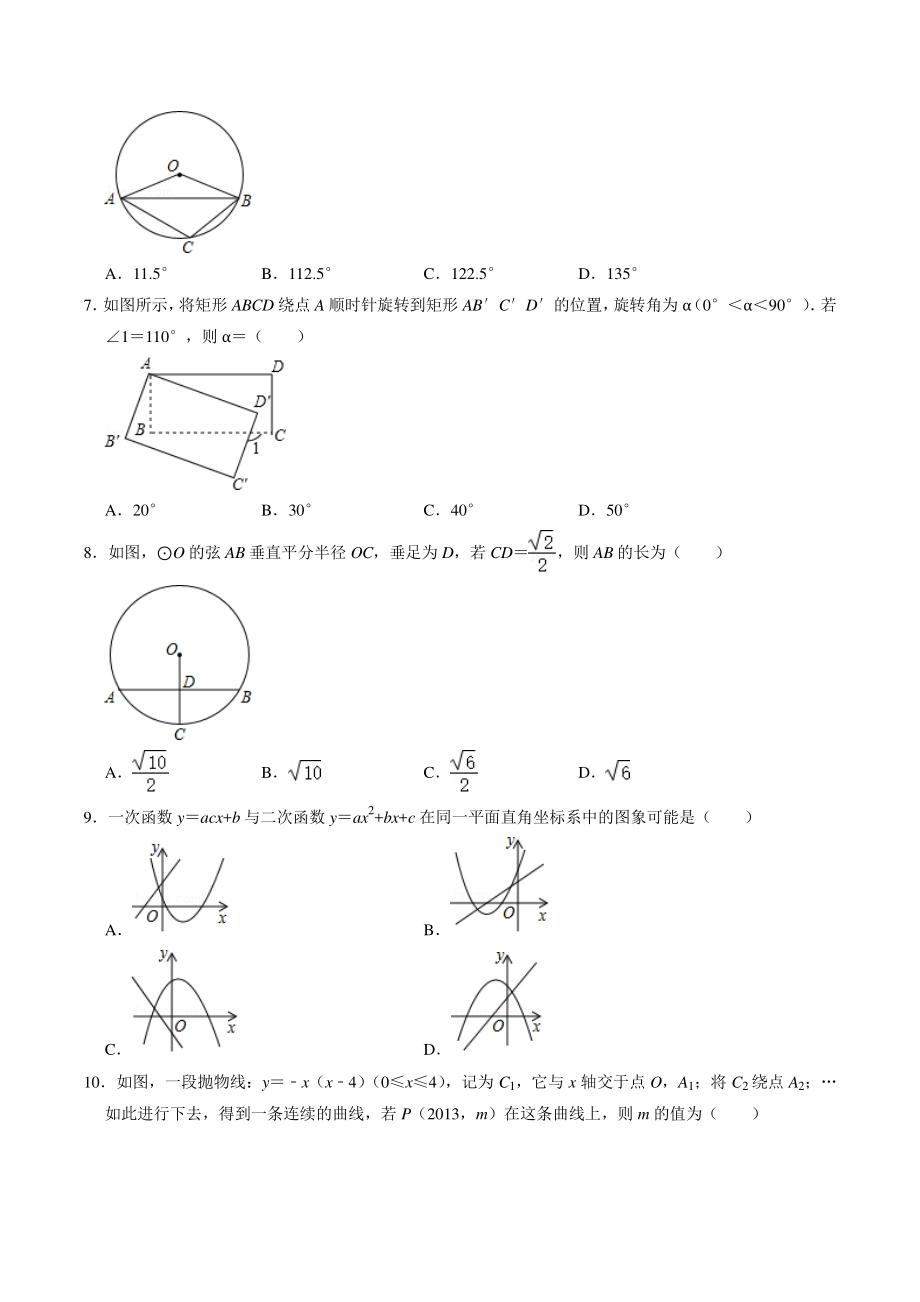
2、两个相等的实数根 C无实数根 D只有一个实数根 5国家统计局统计数据显示，我国快递业务收入逐年增加2017 年至 2019 年我国快递业务收入由 5000 亿元增加到 7500 亿元 设我国 2017 年至 2019 年快递业务收入的年平均增长率为 x， 则可列方程为 （ ） A5000（1+2x）7500 B50002（1+x）7500 C5000（1+x）27500 D5000+5000（1+x）+5000（1+x）27500 6如图，A、B、C 在O 上，OAB22.5，则ACB 的度数是（ ） A11.5 B112.5 C122.5 D135 7 如图所示， 将矩形 ABCD 绕点 A
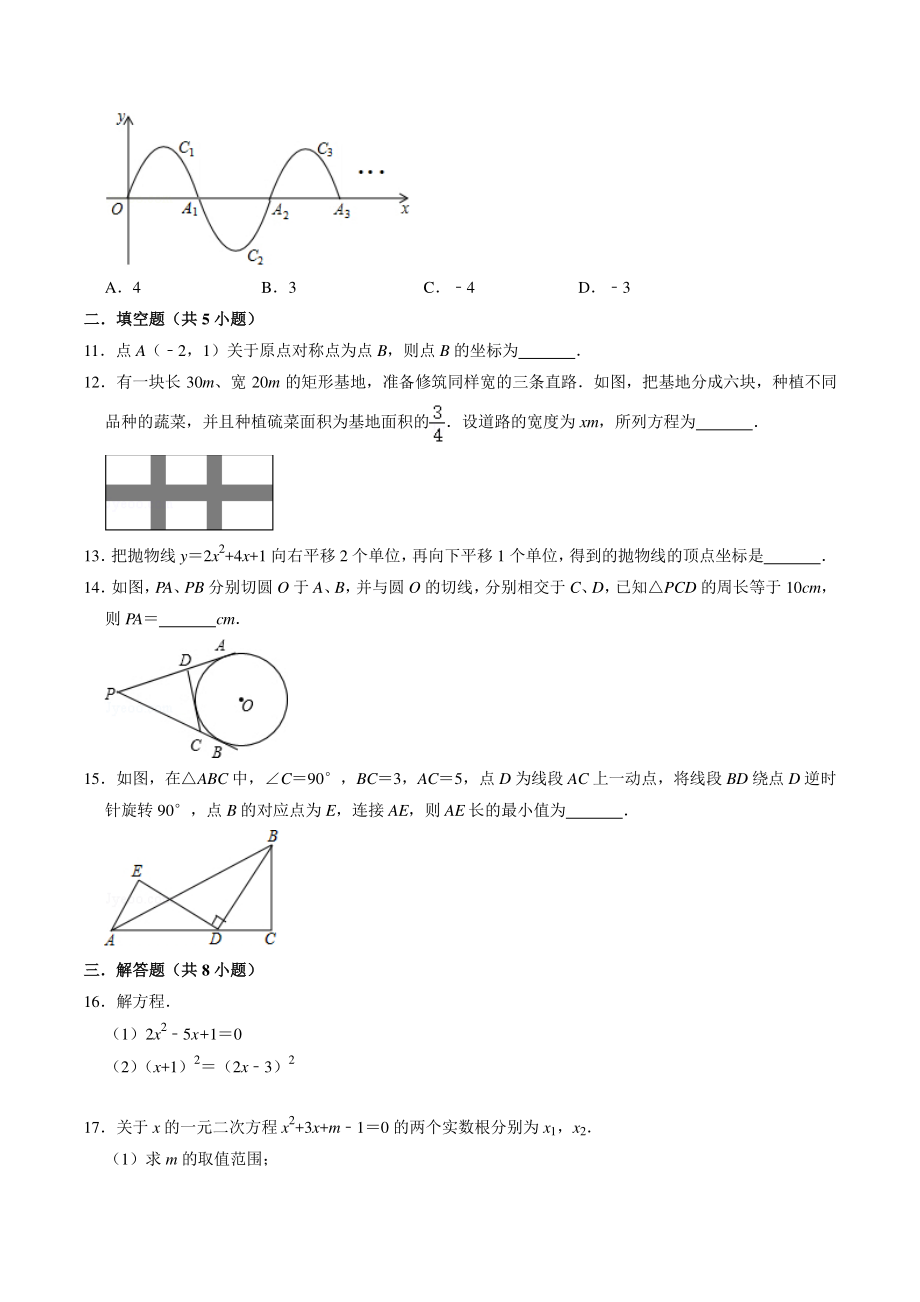
3、 顺时针旋转到矩形 ABCD的位置， 旋转角为 （090） 若1110，则 （ ） A20 B30 C40 D50 8如图，O 的弦 AB 垂直平分半径 OC，垂足为 D，若 CD，则 AB 的长为（ ） A B C D 9一次函数 yacx+b 与二次函数 yax2+bx+c 在同一平面直角坐标系中的图象可能是（ ） A B C D 10如图，一段抛物线：yx（x4） （0 x4） ，记为 C1，它与 x 轴交于点 O，A1；将 C2绕点 A2；如此进行下去，得到一条连续的曲线，若 P（2013，m）在这条曲线上，则 m 的值为（ ） A4 B3 C4 D3 二填空题（共二填空题（共 5 小
4、题）小题） 11点 A（2，1）关于原点对称点为点 B，则点 B 的坐标为 12有一块长 30m、宽 20m 的矩形基地，准备修筑同样宽的三条直路如图，把基地分成六块，种植不同品种的蔬菜，并且种植硫菜面积为基地面积的设道路的宽度为 xm，所列方程为 13 把抛物线 y2x2+4x+1 向右平移 2 个单位， 再向下平移 1 个单位， 得到的抛物线的顶点坐标是 14 如图， PA、 PB 分别切圆 O 于 A、 B， 并与圆 O 的切线， 分别相交于 C、 D， 已知PCD 的周长等于 10cm，则 PA cm 15如图，在ABC 中，C90，BC3，AC5，点 D 为线段 AC 上一动点，将线
5、段 BD 绕点 D 逆时针旋转 90，点 B 的对应点为 E，连接 AE，则 AE 长的最小值为 三解答题（共三解答题（共 8 小题）小题） 16解方程 （1）2x25x+10 （2） （x+1）2（2x3）2 17关于 x 的一元二次方程 x2+3x+m10 的两个实数根分别为 x1，x2 （1）求 m 的取值范围； （2）若 2（x1+x2）+x12x22100，求 m 的值 18如图，在平面直角坐标系中，ABC 的三个顶点坐标分别为 A（2，1） 、B（3，2） 、C（1，4） （1）画出ABC 关于点 C 成中心对称的A1B1C1 （2）画出ABC 绕 C 点逆时针旋转 90后得到的A
6、2B2C 19如图，点 A、B、C 分别是O 上的点，B60，AC3，CD 是O 的直径，P 是 CD 延长线上的一点，且 APAC （1）求证：AP 是O 的切线； （2）求 PD 的长 20在 2020 年中国足球超级联赛前夕，大连赛区某体育用品店购进一批单价为 40 元的球服，如果按单价60 元销售，那么一个月内可售出 240 套，根据销售经验，销售单价每提高 5 元，销售量相应减少 20 套。 （1）当销售单价为多少元时，才能在一个月内获得 6000 元的利润？ （2）当销售单价为多少元时，才能在一个月内获得最大利润？最大利润是多少？ 21一块三角形材料如图所示，A30，C90，AB1
7、2，用这块材料剪出一个矩形 CDEF，其中D、E、F 分别在 BC、AB、AC 上 （1）若设 AEx，则 AF ； （用含 x 的代数式表示） （2）要使剪出的矩形 CDEF 的面积最大，点 E 应选在何处？ 22如图 1，在 RtABC 中，A90，ABAC，点 D，E 分别在边 AB，AC 上，ADAE，连接 DC，点 M，P，N 分别为 DE，DC，BC 的中点 （1）观察猜想：图 1 中，线段 PM 与 PN 的数量关系是 ，位置关系是 ； （2）探究证明：把ADE 绕点 A 逆时针方向旋转到图 2 的位置，连接 MN，BD，CE，判断PMN 的形状，并说明理由； （3）拓展延伸：把
8、ADE 绕点 A 在平面内自由旋转，若 AD4，AB10，请直接写出PMN 周长的最小值 23如图，抛物线 yx2+2x+c 与 x 轴正半轴，y 轴正半轴分别交于点 A，B，且 OAOB，点 G 为抛物线的顶点 （1）求抛物线的解析式及点 G 的坐标； （2）点 M，N 为抛物线上两点（点 M 在点 N 的左侧） ，且到对称轴的距离分别为 3 个单位长度和 5 个单位长度，点 Q 为抛物线上点 M，N 之间（含点 M，N）的一个动点，求点 Q 的纵坐标 yQ的取值范围 （3） 点 E 是直线 AB 上方抛物线上的一动点， 当ABE 的面积最大时， 请直接写出点 E 的坐标和ABE面积的最大值
9、。 河南省安阳市五校联考河南省安阳市五校联考 2020-2021 学年九年级上数学期中试卷学年九年级上数学期中试卷 一选择题（共一选择题（共 10 小题）小题） 1下列防控疫情的图标中，既是轴对称图形，又是中心对称图形的是（ ） A B C D 【分析】根据轴对称图形与中心对称图形的概念判断 【解答】解：A、不是轴对称图形，也不是中心对称图形； B、不是轴对称图形，也不是中心对称图形； C、是轴对称图形，但不是中心对称图形； D、既是轴对称图形，又是中心对称图形 故选：D 【点评】本题考查的是中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要
10、寻找对称中心，旋转 180 度后两部分重合 2若关于 x 的一元二次方程（a+1）x2+x+a210 的一个根是 0，则 a 的值为（ ） A1 B1 C1 或1 D 【分析】把 x0 代入方程（a+1）x2+x+a210 得出 a210，求出 a1，再根据一元二次方程的定义判断即可 【解答】解：把 x0 代入方程（a+1）x2+x+a210 得：a210， 解得：a1， 方程为一元二次方程， a+10， a1， a1， 故选：A 【点评】本题考查了一元二次方程的解和一元二次方程的定义的应用，关键是能根据题意得出方程 a210 和 a+10 3如图，AB 是O 的弦，点 C 在圆上，已知AOB
11、100，则C（ ） A40 B50 C60 D80 【分析】利用圆周角定理可知AOB2ACB，可求得ACB50 【解答】解： AOB 和ACB 是弧 AB 所对的角， AOB2ACB， AOB100， ACB50， 故选：B 【点评】本题主要考查圆周角定理，掌握在同圆或等圆中同弧所对的圆周角是圆心角的一半是解题的关键 4 定义运算： mnmn2mn1 例如： 424224217 则方程 1x0 的根的情况为 （ ） A有两个不相等的实数根 B有两个相等的实数根 C无实数根 D只有一个实数根 【分析】根据新定义运算法则以及即可求出答案 【解答】解：由题意可知：1xx2x10， 141（1）50，
12、 有两个不相等的实数根 故选：A 【点评】本题考查根的判别式，解题的关键是正确理解新定义运算法则，本题属于基础题型 5国家统计局统计数据显示，我国快递业务收入逐年增加2017 年至 2019 年我国快递业务收入由 5000 亿元增加到 7500 亿元 设我国 2017 年至 2019 年快递业务收入的年平均增长率为 x， 则可列方程为 （ ） A5000（1+2x）7500 B50002（1+x）7500 C5000（1+x）27500 D5000+5000（1+x）+5000（1+x）27500 【分析】根据题意可得等量关系：2017 年的快递业务量（1+增长率）22019 年的快递业务量，
13、根据等量关系列出方程即可 【解答】解：设我国 2017 年至 2019 年快递业务收入的年平均增长率为 x， 由题意得：5000（1+x）27500， 故选：C 【点评】此题主要考查了由实际问题抽象出一元二次方程，关键是掌握平均变化率的方法，若设变化前的量为 a，变化后的量为 b，平均变化率为 x，则经过两次变化后的数量关系为 a（1x）2b 6如图，A、B、C 在O 上，OAB22.5，则ACB 的度数是（ ） A11.5 B112.5 C122.5 D135 【分析】由条件可求得AOB135，在优弧 AB 上任取点 E，则可求得AEB，再由圆内接四边形对角互补可求得ACB 【解答】解：OA
14、OB， OABOBA22.5， AOB135， 在优弧 AB 上任取点 E，连接 AE、BE， 则AEBAOB67.5， 又AEB+ACB180， ACB112.5， 故选：B 【点评】本题主要考查圆周角定理及圆内接四边形的性质，掌握圆心角和圆周角之间的关系是解题的关键 7 如图所示， 将矩形 ABCD 绕点 A 顺时针旋转到矩形 ABCD的位置， 旋转角为 （090） 若1110，则 （ ） A20 B30 C40 D50 【分析】 根据矩形的性质得BDBAD90， 根据旋转的性质得DD90， 4，利用对顶角相等得到12110，再根据四边形的内角和为 360可计算出370，然后利用互余即可得
15、到 的度数 【解答】解：如图，四边形 ABCD 为矩形， BDBAD90， 矩形 ABCD 绕点 A 顺时针旋转得到矩形 ABCD， DD90，4， 12110， 3360909011070， 4907020， 20 故选：A 【点评】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角也考查了矩形的性质 8如图，O 的弦 AB 垂直平分半径 OC，垂足为 D，若 CD，则 AB 的长为（ ） A B C D 【分析】连接 OC，由题意即可推出 OC 的长度可得 OA 的长度，运用勾股定理即可推出 AD 的长度，然后，通过垂径定理即可推
16、出 AB 的长度 【解答】解：连接 OA， O 的弦 AB 垂直平分半径 OC，CD， OC， OA， OCAB， AD， AB2AD， AB 故选：D 【点评】本题主要考查垂径定理、勾股定理的应用，关键在于正确地作出辅助线构建直角三角形，认真地进行计算 9一次函数 yacx+b 与二次函数 yax2+bx+c 在同一平面直角坐标系中的图象可能是（ ） A B C D 【分析】先由二次函数 yax2+bx+c 的图象得到字母系数的正负，再与一次函数 yacx+b 的图象相比较看是否一致 【解答】解：A、由抛物线可知，a0，b0，c0，则 ac0，由直线可知，ac0，b0，故本选项不合题意； B
17、、由抛物线可知，a0，b0，c0，则 ac0，由直线可知，ac0，b0，故本选项符合题意； C、由抛物线可知，a0，b0，c0，则 ac0，由直线可知，ac0，b0，故本选项不合题意； D、由抛物线可知，a0，b0，c0，则 ac0，由直线可知，ac0，b0，故本选项不合题意 故选：B 【点评】本题考查二次函数和一次函数的图象，解题的关键是明确一次函数和二次函数性质 10如图，一段抛物线：yx（x4） （0 x4） ，记为 C1，它与 x 轴交于点 O，A1；将 C2绕点 A2；如此进行下去，得到一条连续的曲线，若 P（2013，m）在这条曲线上，则 m 的值为（ ） A4 B3 C4 D3
18、【分析】根据抛物线与 x 轴的交点问题，得到图象 C1与 x 轴交点坐标为： （0，0） ， （4，0） ，再利用旋转的性质得到图象 C2与 x 轴交点坐标为： （4，0） ， （8，0） ，则抛物线 C2：y（x4） （x8） （4x8） ，于是可推出抛物线 C504：y（x4503） （x4504） （2012x2016） ，由于 20134503+1，则可判断 P（2013，m）在抛物线 y（x4503） （x504） （2012x2016）上，然后根据二次函数图象上点的坐标特征计算 m 的值 【解答】解：一段抛物线 C1：yx（x4） （0 x4） ， 图象 C1与 x 轴交点坐标为：
19、 （0，0） ， （4，0） ， 将 C1绕点 A1旋转 180得 C2，交 x 轴于点 A2； ， 抛物线 C2：y（x4） （x8） （4x8） ， 将 C2绕点 A2旋转 180得 C3，交 x 轴于点 A3； 如此进行下去， 抛物线 C504：y（x4503） （x4504） （2012x2016） ， 20134503+1， P（2013，m）在抛物线 y（x4503） （x504） （2012x2016）上， 当 x2013 时，m（20132012） （20132016）3 故选：D 【点评】本题考查了二次函数与几何变换：由于抛物线平移后的形状不变，故 a 不变，所以求平移后的抛
20、物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式 二填空题（共二填空题（共 5 小题）小题） 11点 A（2，1）关于原点对称点为点 B，则点 B 的坐标为 （2，1） 【分析】平面直角坐标系中任意一点 P（x，y） ，关于原点的对称点是（x，y） ，记忆方法是结合平面直角坐标系的图形记忆 【解答】解：点 A（2，1）关于原点对称点为点 B，点 B 的坐标为（2，1） 【点评】关于原点对称的点坐标的关系，是需要识记的基本问题 12有一块长 30m、宽 20m 的矩形基地，准备修筑同样宽的三条直路如图，把基
21、地分成六块，种植不同品种的蔬菜， 并且种植硫菜面积为基地面积的 设道路的宽度为 xm， 所列方程为 （302x） （20 x）3020 【分析】设道路的宽度为 xm，则六块菜地可合成长为（302x）m，宽为（20 x）m 的矩形，根据矩形的面积公式结合种植硫菜面积为基地面积的，即可得出关于 x 的一元二次方程，此题得解 【解答】解：设道路的宽度为 xm，则六块菜地可合成长为（302x）m，宽为（20 x）m 的矩形， 根据题意得： （302x） （20 x）3020 故答案为： （302x） （20 x）3020 【点评】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方
22、程是解题的关键 13把抛物线 y2x2+4x+1 向右平移 2 个单位，再向下平移 1 个单位，得到的抛物线的顶点坐标是 （1，2） 【分析】 先写成平移前的抛物线的顶点坐标， 再根据向右平移横坐标加， 向下平移， 纵坐标减解答即可 【解答】解：抛物线 y2x2+4x+12（x+1）21， 顶点坐标为（1，1） ， 向右平移 2 个单位，向下平移 1 个单位， 所得抛物线的顶点坐标为（1，2） ， 故答案为： （1，2） 【点评】本题考查了二次函数图形与几何变换，是基础题，掌握平移规律“左加右减，上加下减”是解题的关键 14 如图， PA、 PB 分别切圆 O 于 A、 B， 并与圆 O 的切
23、线， 分别相交于 C、 D， 已知PCD 的周长等于 10cm，则 PA 5 cm 【分析】 由于 DA、 DC、 BC 都是O 的切线， 可根据切线长定理， 将PCD 的周长转换为 PA、 PB 的长，然后再进行求解 【解答】解：如图，设 DC 与O 的切点为 E； PA、PB 分别是O 的切线，且切点为 A、B； PAPB； 同理，可得：DEDA，CECB； 则PCD 的周长PD+DE+CE+PCPD+DA+PC+CBPA+PB10（cm） ； PAPB5cm， 故答案为：5 【点评】此题主要考查了切线长定理的应用，能够将PCD 的周长转换为切线 PA、PB 的长是解答此题的关键 15如图
24、，在ABC 中，C90，BC3，AC5，点 D 为线段 AC 上一动点，将线段 BD 绕点 D 逆时针旋转 90，点 B 的对应点为 E，连接 AE，则 AE 长的最小值为 【分析】由旋转的性质可知 BDDE，C90，则容易想到构造一个直角三角形与 RtBCD 全等，即过 E 点作 EHAD 于点 H，设 CDx，则可用 x 表示 AE 的长，从而判断什么时候 AE 取得最小值 【解答】解：设 CDx，则 AD5x， 过点 E 作 EHAD 于点 H，如图： 由旋转的性质可知 BDDE， ADE+BDC90，BDC+CBD90， ADECBD， 又EHDC， BCDDHE， EHCDx，DHB
25、C3 AD5x， AHADDH5x32x， 在 RtAEH 中，AE2AH2+EH2（2x）2+x22x2+4x+42（x1）2+2， 所以当 x1 时，AE2取得最小值 2，即 AE 取得最小值 故答案为： 【点评】本题考查了全等三角形的性质和判定，旋转的性质和勾股定理等知识点，能灵活运用知识点进行推理是解此题的关键 三解答题（共三解答题（共 8 小题）小题） 17关于 x 的一元二次方程 x2+3x+m10 的两个实数根分别为 x1，x2 （1）求 m 的取值范围； （2）若 2（x1+x2）+x12x22100，求 m 的值 【分析】 （1）根据一元二次方程的根的判别式的意义得到324（
26、m1）0，然后解不等式即可得到 m 的取值范围； （2）根据根与系数的关系得到 x1+x23，x1x2m1，则有 2（3）+（m1）2100，解得m15，m23，然后根据（1）的范围确定 m 的值 【解答】解： （1）根据题意得324（m1）0，解得 m， 所以 m 的取值范围为 m； （2）根据题意得 x1+x23，x1x2m1， ， 2（3）+（m1）2100，解得 m15，m23， m， m3 【点评】本题考查了一元二次方程 ax2+bx+c0（a0）的根与系数的关系：若方程两个为 x1，x2，则x1+x2，x1x2也考查了一元二次方程的根的判别式 18如图，在平面直角坐标系中，ABC
27、的三个顶点坐标分别为 A（2，1） 、B（3，2） 、C（1，4） （1）以原点 O 为位似中心，在第二象限内画出将ABC 放大为原来的 2 倍后的A1B1C1 （2）画出ABC 绕 C 点逆时针旋转 90后得到的A2B2C 【分析】 （1）把点 A、B、C 的横纵坐标都乘以 2 得到 A1、B1、C1的坐标，然后描点即可； （2）利用网格特点和旋转的性质画出点 A、B 的对应点 A2、B2即可得到A2B2C 【解答】解： （1）如图，A1B1C1为所作； （2）如图，A2B2C 为所作； 【点评】本题考查了作图位似变换：利用以原点为位似中心的对应点的坐标之间的关系写出所求图形各顶点坐标，然后
28、描点即可也考查了旋转变换 19如图，点 A、B、C 分别是O 上的点，B60，AC3，CD 是O 的直径，P 是 CD 延长线上的 一点，且 APAC （1）求证：AP 是O 的切线； （2）求 PD 的长 【分析】 （1）首先连接 OA，由B60，利用圆周角定理，即可求得AOC 的度数，又由 OAOC，即可求得OAC 与OCA 的度数，利用三角形外角的性质，求得AOP 的度数，又由 APAC，利用等边对等角，求得P，则可求得PAO90，则可证得 AP 是O 的切线； （2）由 CD 是O 的直径，即可得DAC90，然后利用三角函数与等腰三角形的判定定理，即可求得 PD 的长 【解答】 （1）
29、证明：连接 OA B60， AOC2B120， 又OAOC， ACPCAO30， AOP60， APAC， PACP30， OAP90， OAAP， AP 是O 的切线， （2）解：连接 AD CD 是O 的直径， CAD90， ADACtan303， ADCB60， PADADCP603030， PPAD， PDAD 【点评】此题考查了切线的判定、圆周角定理、等腰三角形的判定与性质以及三角函数等知识此题难度适中，解题的关键是准确作出辅助线，注意数形结合思想的应用 21一块三角形材料如图所示，A30，C90，AB12，用这块材料剪出一个矩形 CDEF，其中D、E、F 分别在 BC、AB、AC
30、上 （1）若设 AEx，则 AF x ； （用含 x 的代数式表示） （2）要使剪出的矩形 CDEF 的面积最大，点 E 应选在何处？ 【分析】 （1）在直角三角形中，利用 30 度所对的直角边等于斜边的一半表示出 EF，再利用勾股定理表示出 AF 即可； （2）利用 30 度所对的直角边等于斜边的一半表示出 BC，进而利用勾股定理表示出 AC，由 ACAF 表示出 CF，根据 CF 与 EF 乘积列出 S 与 x 的二次函数解析式，利用二次函数性质确定出面积的最大值，以及此时 x 的值即可 【解答】解： （1）在 RtABC 中，A30，C90，AEx， EFx， 根据勾股定理得：AFx；
31、故答案为：x； （2）四边形 CDEF 是矩形， AFE90， A30， EFAEx， 在 RtABC 中，C90，AB12， BCAB6， 根据勾股定理得：AC6， CFACAF6x， S矩形CDEFCFEFx（6x）（x6）2+9， 当 x6 时，矩形 CDEF 的面积最大， 即当点 E 为 AB 的中点时，矩形 CDEF 的面积最大 【点评】此题考查了相似三角形的应用，二次函数的最值，勾股定理，含 30 度直角三角形的性质，以及矩形的性质，熟练掌握性质及定理是解本题的关键 22如图 1，在 RtABC 中，A90，ABAC，点 D，E 分别在边 AB，AC 上，ADAE，连接 DC，点
32、M，P，N 分别为 DE，DC，BC 的中点 （1）观察猜想：图 1 中，线段 PM 与 PN 的数量关系是 PMPN ，位置关系是 PMPN ； （2）探究证明：把ADE 绕点 A 逆时针方向旋转到图 2 的位置，连接 MN，BD，CE，判断PMN 的形状，并说明理由； （3）拓展延伸：把ADE 绕点 A 在平面内自由旋转，若 AD4，AB10，请直接写出PMN 面积的最大值 【分析】 （1）利用三角形的中位线得出 PMCE，PNBD，进而判断出 BDCE，即可得出结论，再利用三角形的中位线得出 PMCE 得出DPMDCA，最后用互余即可得出结论； （2）先判断出ABDACE，得出 BDCE
33、，同（1）的方法得出 PMBD，PNBD，即可得出PMPN，同（1）的方法即可得出结论； （3） 方法 1、 先判断出 MN 最大时， PMN 的面积最大， 进而求出 AN， AM， 即可得出 MN 最大AM+AN，最后用面积公式即可得出结论 方法 2、先判断出 BD 最大时，PMN 的面积最大，而 BD 最大是 AB+AD14，即可 【解答】解： （1）点 P，N 是 BC，CD 的中点， PNBD，PNBD， 点 P，M 是 CD，DE 的中点， PMCE，PMCE， ABAC，ADAE， BDCE， PMPN， PNBD， DPNADC， PMCE， DPMDCA， BAC90， ADC
34、+ACD90， MPNDPM+DPNDCA+ADC90， PMPN， 故答案为：PMPN，PMPN， （2）由旋转知，BADCAE， ABAC，ADAE， ABDACE（SAS） ， ABDACE，BDCE， 同（1）的方法，利用三角形的中位线得，PNBD，PMCE， PMPN， PMN 是等腰三角形， 同（1）的方法得，PMCE， DPMDCE， 同（1）的方法得，PNBD， PNCDBC， DPNDCB+PNCDCB+DBC， MPNDPM+DPNDCE+DCB+DBC BCE+DBCACB+ACE+DBC ACB+ABD+DBCACB+ABC， BAC90， ACB+ABC90， MPN
35、90， PMN 是等腰直角三角形， （3）方法 1、如图 2，同（2）的方法得，PMN 是等腰直角三角形， MN 最大时，PMN 的面积最大， DEBC 且 DE 在顶点 A 上面， MN 最大AM+AN， 连接 AM，AN， 在ADE 中，ADAE4，DAE90， AM2， 在 RtABC 中，ABAC10，AN5， MN最大2+57， SPMN最大PM2MN2（7）2 方法 2、由（2）知，PMN 是等腰直角三角形，PMPNBD， PM 最大时，PMN 面积最大， 点 D 在 BA 的延长线上， BDAB+AD14， PM7， SPMN最大PM272 【点评】此题是几何变换综合题，主要考查
36、了三角形的中位线定理，等腰直角三角形的判定和性质，全等三角形的判断和性质，直角三角形的性质，解（1）的关键是判断出 PMCE，PNBD，解（2） 的关键是判断出ABDACE，解（3）的关键是判断出 BD 最大时，PMN 的面积最大，是一道中考常考题 23如图，抛物线 yx2+2x+c 与 x 轴正半轴，y 轴正半轴分别交于点 A，B，且 OAOB，点 G 为抛物线的顶点 （1）求抛物线的解析式及点 G 的坐标； （2）点 M，N 为抛物线上两点（点 M 在点 N 的左侧） ，且到对称轴的距离分别为 3 个单位长度和 5 个单位长度，点 Q 为抛物线上点 M，N 之间（含点 M，N）的一个动点，
37、求点 Q 的纵坐标 yQ的取值范围 【分析】 （1）先求出点 B，点 A 坐标，代入解析式可求 c 的值，即可求解； （2）先求出点 M，点 N 坐标，即可求解 【解答】解： （1）抛物线 yx2+2x+c 与 y 轴正半轴交于点 B， 点 B（0，c） ， OAOBc， 点 A（c，0） ， 0c2+2c+c， c3 或 0（舍去） ， 抛物线解析式为：yx2+2x+3， yx2+2x+3（x1）2+4， 顶点 G 的坐标为（1，4） ； （2）yx2+2x+3（x1）2+4， 对称轴为直线 x1， 点 M，N 为抛物线上两点（点 M 在点 N 的左侧） ，且到对称轴的距离分别为 3 个单位
38、长度和 5 个单位长度， 点 M 的横坐标为2 或 4，点 N 的横坐标为 6， 点 M 坐标为（2，5）或（4，5） ，点 N 坐标为（6，21） ， 点 Q 为抛物线上点 M，N 之间（含点 M，N）的一个动点， 21yQ4 或21yQ5 【点评】本题考查了待定系数法求二次函数解析式，二次函数的性质，二次函数图象上点的坐标特征， 熟练运用二次函数的性质解决问题是本题的关键 声明：试题解析著 作权属菁优网 所有，未经书 面同意，不得 复制发布 日期：2020/11/12 20:37:19 ；用户：晚街 听风。；邮箱 ：orFmNt3bOnnF1 hStx-WKMahvC； 学号：2942001 3
