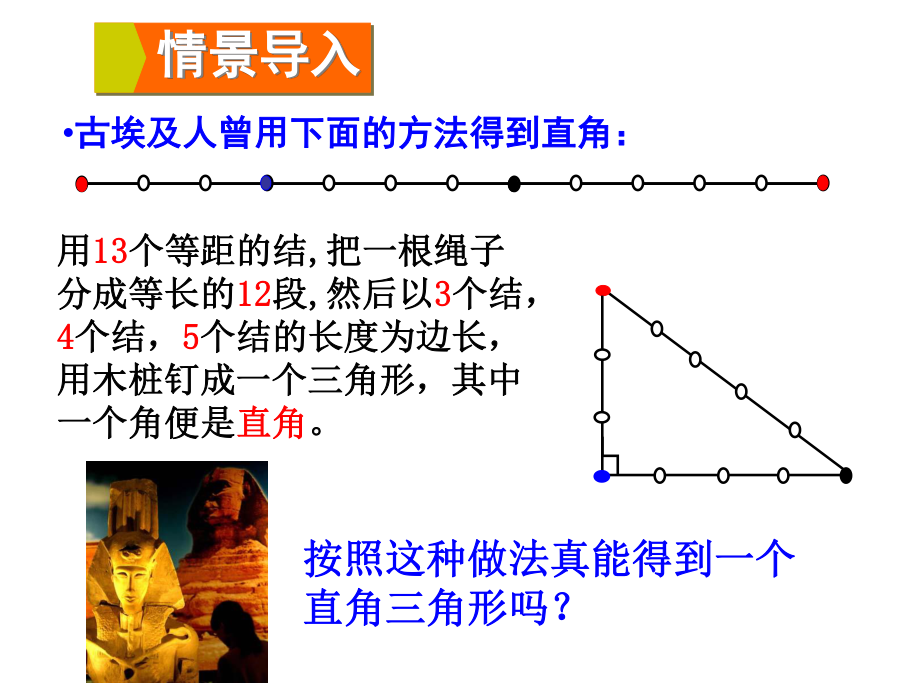
1、如果直角三角形两直角边分别为如果直角三角形两直角边分别为a a，b b，斜边为，斜边为c c，那么有，那么有 a2 + b2 = c2 勾股定理勾股定理 互逆命题 如果三角形的三边长如果三角形的三边长a a、b b、c c满足满足 那么这个三角形是直角三角形。那么这个三角形是直角三角形。 a2 + b2 = c2 复习回顾复习回顾 按照这种做法真能得到一个按照这种做法真能得到一个直角三角形吗？直角三角形吗？ 古埃及人曾用下面的方法得到直角：古埃及人曾用下面的方法得到直角： 用用1313个等距的结个等距的结, ,把一根绳子把一根绳子分成等长的分成等长的1212段段, ,然后以然后以3 3个结，个
2、结，4 4个结，个结，5 5个结的长度为边长，个结的长度为边长，用木桩钉成一个三角形，其中用木桩钉成一个三角形，其中一个角便是一个角便是直角直角。 情景导入情景导入 3 4 5 请同学们观察请同学们观察,这个三角形的三条这个三角形的三条边有什么关系吗边有什么关系吗? 3 3 2 2 4 4 2 2 5 5 2 2 + + = = 6 6，8 8，10. 5, 12, 1310. 5, 12, 13 （1）这三组数都满足）这三组数都满足 222cba 吗？吗？ （2）画出图形）画出图形,它们都是直角三角形吗？它们都是直角三角形吗？ 探索新知探索新知 下面的三组数分别是一个三角形的三边长下面的三组
3、数分别是一个三角形的三边长a，b，c 由上面几个例子你发现了什么吗由上面几个例子你发现了什么吗? ?请以命题的请以命题的 形式说出你的观点形式说出你的观点! ! 命题2 如果三角形的三边长如果三角形的三边长a a、b b、c c满足满足 那么这个三角形是直角三角形。那么这个三角形是直角三角形。 a2 + b2 = c2 3 3 4 4 5 5 A A C C B B A A B B C C 3 3 4 4 古埃及人的做法：古埃及人的做法： ABCABC中，中， BC=3BC=3、 AC=4AC=4、AB=5AB=5 这两个三角形有什么关系？这两个三角形有什么关系？ 我们作我们作RtRtABAB
4、C C， 使使A AC C=AC=AC，B BC C=BC=BC 3 3 4 4 5 5 A A C C B B A A B B C C 3 3 4 4 在在 RtRtABCABC中中根据勾股定理有根据勾股定理有 222CBCABA55434, 32222BABACACBABC CBA90CC勾股定理的逆命题勾股定理的逆命题 如果直角三角形两直角边分别为如果直角三角形两直角边分别为a，b，斜，斜边为边为c，那么，那么 a2 + b2 = c2 如果三角形的三边长如果三角形的三边长a、b、c满足满足 那么这个三角形是直角三角形。且边那么这个三角形是直角三角形。且边C所所对的角为直角。对的角为直角
5、。 a2 + b2 = c2 互逆命题 逆定理 定理 勾股定理勾股定理 1.1.判断由判断由a a、b b、c c组成的三角形是不是直角三角形：组成的三角形是不是直角三角形： (1) a(1) a15 , b 15 , b 8 , 8 , c c1717 (2) a(2) a13 , b 13 , b 15 , 15 , c c1414 分析：由勾股定理的逆定理，判断三角形是不是直角三角分析：由勾股定理的逆定理，判断三角形是不是直角三角形，只要看两条形，只要看两条较小边较小边的平方和是否等于的平方和是否等于最大边最大边的平方。的平方。 解：解：1528222564289 172289 1528
6、2172 这个三角形是直角三角形这个三角形是直角三角形 当堂训练当堂训练 常用的勾股数常用的勾股数 3，4，5 6，8，10 5，12，13 7，24，25 8，15，17 9，40，41 9，12，15 10，24，26 200，480，520 像像25,20,15,25,20,15,能够成为直角三角形三能够成为直角三角形三条边长的三个正整数，称为条边长的三个正整数，称为勾股数勾股数. . (3) a=1 b=2 c= _ _ ; 3 下面以下面以a,b,ca,b,c为边长的三角形是不是直角三角为边长的三角形是不是直角三角形？如果是那么哪一个角是直角？形？如果是那么哪一个角是直角？ (6)
7、a=25 b=20 c=15 _ _ ; (2) a=13 b=14 c=15 _ _ ; (4) a:b: c=3:4:5 _ _ ; 是是 是是 不是不是 是是 C=90C=900 0 B=90B=900 0 C=90C=900 0 (1) a=5 b=12 c=13 _ _ ; (5) a= 8 b=15 c=17 _ _ ; 1、 如果线段如果线段a,b,c能组成直角三角形能组成直角三角形, 则它们的则它们的比可能是比可能是 ( ) A.3:4:7; B. 5:12:13; C. 1:2:4; D. 1:3:5. 2、将直角三角形的三边的长度扩大同样的倍、将直角三角形的三边的长度扩大同
8、样的倍数数,则得到的三角形是则得到的三角形是 ( ) A.是直角三角形是直角三角形; B. 可能是锐角三角形可能是锐角三角形; C. 可能是钝角三角形可能是钝角三角形; D. 不可能是直角三角不可能是直角三角形形. B A 3.下列几组数据能否作为直角三角形的三边？下列几组数据能否作为直角三角形的三边？ （1）9，12，15; （2）15，36，39; （3）12，35，36 ; （4）12，18，22. 4.一个三角形的三边的长分别是一个三角形的三边的长分别是15cm,20cm, 25cm，则这个三角形的面积是（，则这个三角形的面积是（ ）cm2 . (A)250 (B)150 (C)200
9、 (D)不能确定不能确定 5.如图，在如图，在ABC中，中，ADBC于于D，BD=9， AD=12，AC=20，则，则ABC是（是（ ）. (A)等腰三角形等腰三角形 (B)锐角三角形锐角三角形 (C)钝角三角形钝角三角形 (D)直角三角形直角三角形 A B D C 6、三角形的三边分别是、三角形的三边分别是a,b,c, 且满足等式且满足等式(a+b)2-c2=2ab, 则此三角形是则此三角形是: ( ) A. 直角三角形直角三角形; B. 是锐角三角形是锐角三角形; C.是钝角三角形是钝角三角形; D. 是等腰直角三角形是等腰直角三角形. A 学以致用学以致用 拓广与应用 “远航远航”号、号
10、、“海天海天”号轮船同时离开号轮船同时离开港口港口, ,各自沿一固定方向航行各自沿一固定方向航行, , “远航远航”号号每小时航行每小时航行1616海里海里, , “海天海天”号每小时航行号每小时航行1212海里海里. .它们离开港口一个半小时后相距它们离开港口一个半小时后相距3030海里海里. .如果知道如果知道“远航远航”号沿东北方向航行号沿东北方向航行, ,能知道能知道“海天海天”号沿哪个方向航行吗号沿哪个方向航行吗? ? ABABD课堂小结课堂小结 必做题：必做题：教材教材P P1111习题习题4 4、5 5题题 附加题：附加题：练习册（直角三角形练习册（直角三角形三边关系）三边关系）
11、 课后作业课后作业 在数学的天地里，重要的不在数学的天地里，重要的不是我们知道什么，而是我们怎么是我们知道什么，而是我们怎么知道什么。知道什么。毕达哥拉斯毕达哥拉斯 4. 13 A B C D A B C D 3 4 5 12 例例1 : 一个零件的形状如左图所示，按规定一个零件的形状如左图所示，按规定这个零件中这个零件中A和和DBC都应为直角。工人师傅都应为直角。工人师傅量得这个零件各边尺寸如右图所示，这个量得这个零件各边尺寸如右图所示，这个 零件符零件符合要求吗？合要求吗？ A D C B 例：四边形例：四边形ABCD中，已知中，已知AB=3, BC=4, CD=12, DA=13, 且且
12、ABC=90ABC=900 0, ,求这个四求这个四边形的面积边形的面积. . FEDABC1.1.如图，在正方形如图，在正方形ABCDABCD中，中，AB=4AB=4，AE=2AE=2， DF=1DF=1， 图中有几个直角三角形，你是如何判断的？与你的同图中有几个直角三角形，你是如何判断的？与你的同 伴交流。伴交流。 4 4 1 1 2 2 2 2 4 4 3 3 易知易知: :ABEABE，DEFDEF，FCBFCB均为均为RtRt 由勾股定理知由勾股定理知 BEBE2 2=2=22 2+4+42 2=20=20，EFEF2 2=2=22 2+1+12 2=5=5， BFBF2 2=3=32 2+4+42 2=25=25 BEBE2 2+EF+EF2 2=BF=BF2 2 BEF是是Rt
