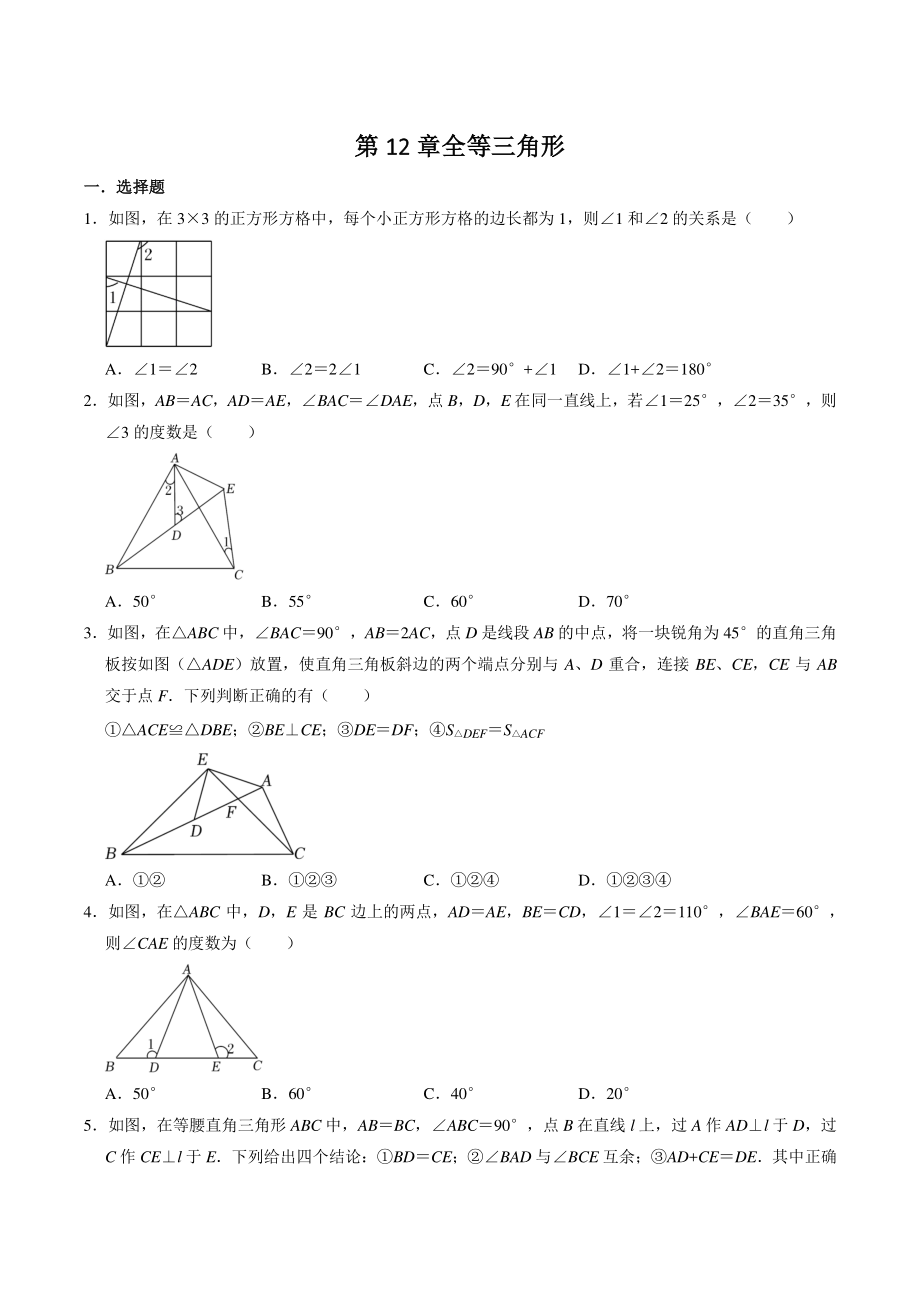
1、 第第 1212 章全等三角形章全等三角形 一选择题一选择题 1如图，在 33 的正方形方格中，每个小正方形方格的边长都为 1，则1 和2 的关系是（ ） A12 B221 C290+1 D1+2180 2如图，ABAC，ADAE，BACDAE，点 B，D，E 在同一直线上，若125，235，则3 的度数是（ ） A50 B55 C60 D70 3如图，在ABC 中，BAC90，AB2AC，点 D 是线段 AB 的中点，将一块锐角为 45的直角三角板按如图（ADE）放置，使直角三角板斜边的两个端点分别与 A、D 重合，连接 BE、CE，CE 与 AB交于点 F下列判断正确的有（ ） ACEDB
2、E；BECE；DEDF；SDEFSACF A B C D 4如图，在ABC 中，D，E 是 BC 边上的两点，ADAE，BECD，12110，BAE60，则CAE 的度数为（ ） A50 B60 C40 D20 5如图，在等腰直角三角形 ABC 中，ABBC，ABC90，点 B 在直线 l 上，过 A 作 ADl 于 D，过C 作 CEl 于 E下列给出四个结论：BDCE；BAD 与BCE 互余；AD+CEDE其中正确 结论的序号是（ ） A B C D 6如图，AD，BE 是ABC 的高线，AD 与 BE 相交于点 F若 ADBD6，且ACD 的面积为 12，则 AF的长度为（ ） A4 B
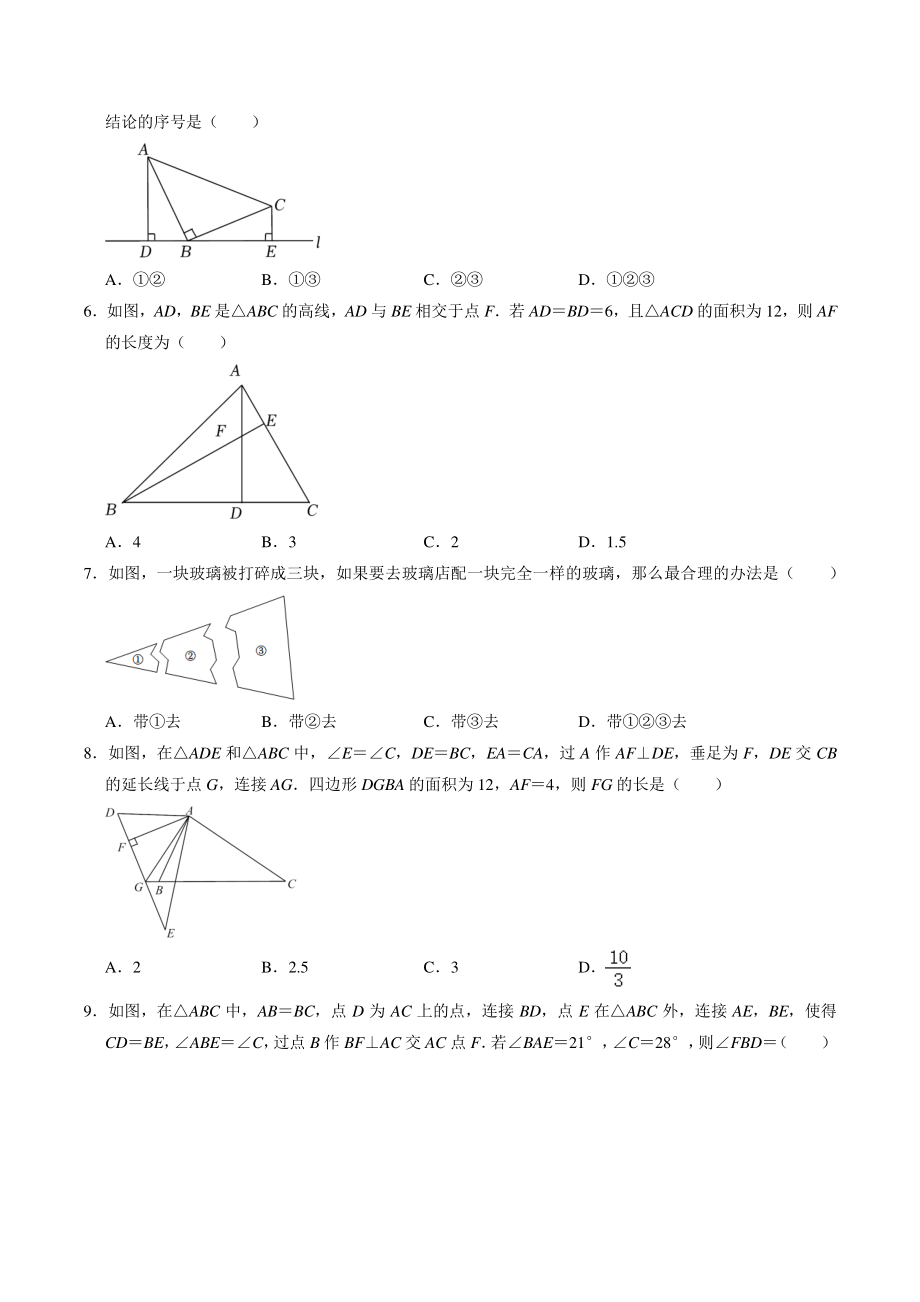
3、3 C2 D1.5 7如图，一块玻璃被打碎成三块，如果要去玻璃店配一块完全一样的玻璃，那么最合理的办法是（ ） A带去 B带去 C带去 D带去 8如图，在ADE 和ABC 中，EC，DEBC，EACA，过 A 作 AFDE，垂足为 F，DE 交 CB的延长线于点 G，连接 AG四边形 DGBA 的面积为 12，AF4，则 FG 的长是（ ） A2 B2.5 C3 D 9如图，在ABC 中，ABBC，点 D 为 AC 上的点，连接 BD，点 E 在ABC 外，连接 AE，BE，使得CDBE， ABEC， 过点 B 作 BFAC 交 AC 点 F 若BAE21， C28， 则FBD （ ） A49
4、 B59 C41 D51 10 如图， 在MPN 中， H 是高 MQ 和 NR 的交点， 且 PMHN， 已知 MH3， PQ2， 则 PN 的长为 （ ） A5 B7 C8 D11 二填空题二填空题 11如图，在ABC 中，ABAC，D，E，F 分别是 BC，AC，AB 上的点，且 BFCD，BDCE，FDE，则A 的度数是 度 （用含 的代数式表示） 12如图，方格纸中是 4 个相同的正方形，婉婷同学在这张方格纸上画了1、2、3 三个角，那么1+2+3 度 13如图 EB 交 AC 于 M，交 FC 于 D，AB 交 FC 于 N，EF90，BC，AEAF给出下列结论：12；BECF；
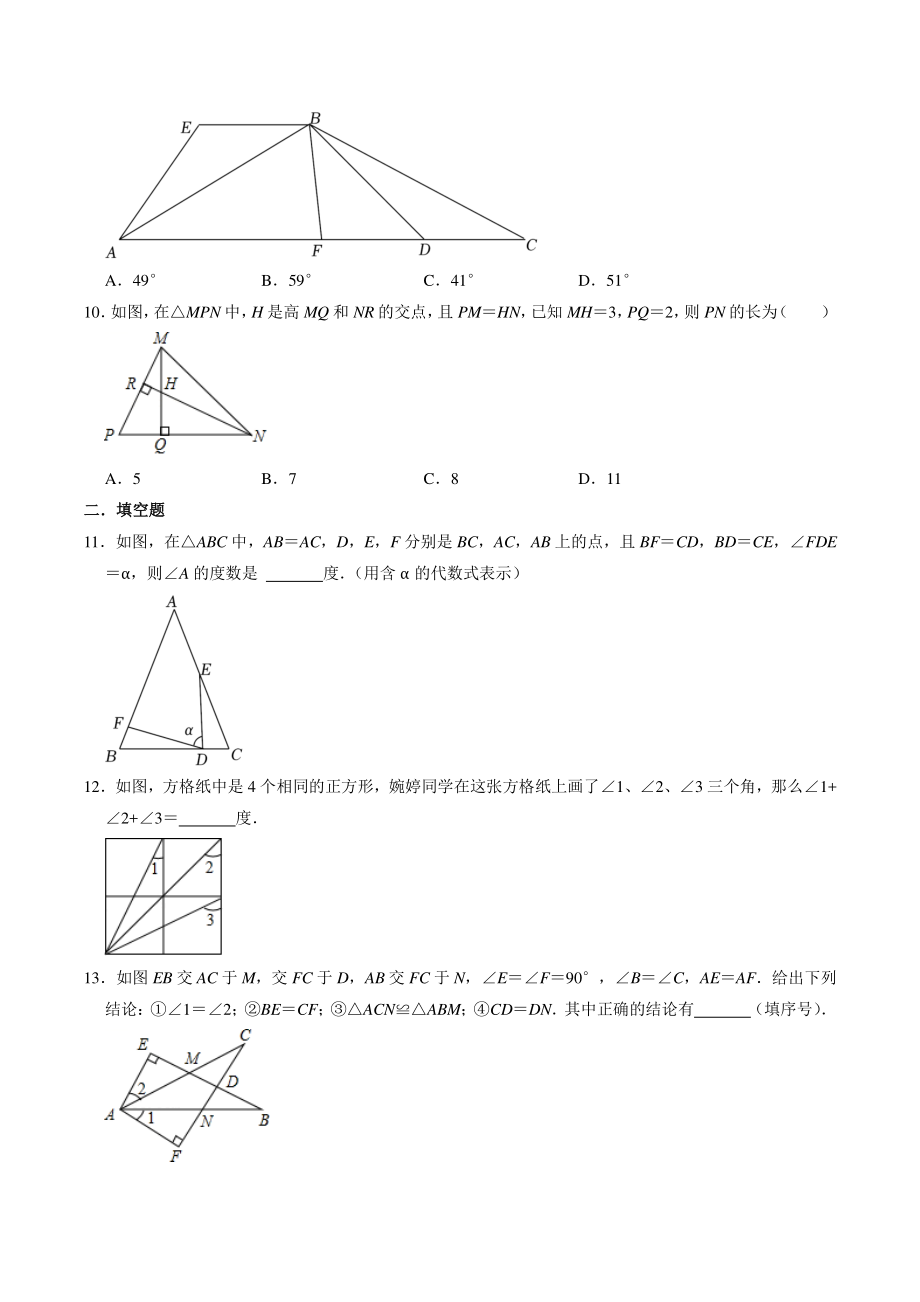
5、ACNABM；CDDN其中正确的结论有 （填序号） 14如图，已知 A、B、C 在同一条直线上，且AC56，ABCE，ADBC，那么BDE 的角度是 15如图，ABC 的面积为 10cm2，AP 垂直B 的平分线 BP 于 P，则BCP 的面积为 cm2 16如图，AEAB，且 AEAB，BCCD，且 BCCD，EF6，BG3，DH4，计算图中实线所围成的图形的面积 S 是 17如图，已知ABCABC，AABC，ABC70，则CBC 三解答题三解答题 18如图，已知 ACBD，EA、EB 分别平分CAB 和DBA，CD 过点 E，求证：ABAC+BD 19如图，已知：在四边形 ABCD 中，过
6、 C 作 CEAB 于 E，并且 CDCB，ABC+ADC180 （1）求证：AC 平分BAD； （2）若 AE9，BE3，求 AD 的长 20如图，四边形 ABCD 中，ABC+D180，AC 平分BAD，CEAB，CFAD 试说明： （1）CBECDF； （2）AB+DFAF 21如图，在ABC 中，AD，CE 分别是 BC、AB 边上的高，AD 与 CE 交于点 F，连接 BF，延长 AD 到点G，使得 AGBC，连接 BG，若 CFAB，BF 与 BG 之间有怎样的关系呢？并说明理由 22如图，在ABC 中，D 为 BC 的中点，过 D 点的直线 GF 交 AC 于点 F，交 AC 的
7、平行线 BG 于点 G，DEGF，并交 AB 于点 E，连接 EG，EF （1）求证：BGCF （2）请你猜想 BE+CF 与 EF 的大小关系，并说明理由 23如图，ABC90，FAAB 于点 A，点 D 在直线 AB 上，ADBC，AFBD （1）如图 1，若点 D 在线段 AB 上，判断 DF 与 DC 的数量关系和位置关系，并说明理由； （2）如图 2，若点 D 在线段 AB 的延长线上，其他条件不变，试判断（1）中结论是否成立，并说明理由 24如图，已知在ABC 中，ABAC，BAC90，分别过 B、C 向过 A 的直线作垂线，垂足分别为 E、F （1）如图过 A 的直线与斜边 BC
8、 不相交时，求证：EFBE+CF； （2）如图过 A 的直线与斜边 BC 相交时，其他条件不变，若 BE10，CF3，求：FE 长 25 【阅读理解】 课外兴趣小组活动时，老师提出了如下问题： 如图 1，ABC 中，若 AB8，AC6，求 BC 边上的中线 AD 的取值范围小明在组内经过合作交流，得到了如下的解决方法：延长 AD 到点 E，使 DEAD，请根据小明的方法思考： （1）由已知和作图能得到ADCEDB 的理由是 ASSS BSAS CAAS DHL （2）求得 AD 的取值范围是 A6AD8 B6AD8 C1AD7 D1AD7 【感悟】 解题时，条件中若出现“中点” “中线”字样，
9、可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中 【问题解决】 （3）如图 2，AD 是ABC 的中线，BE 交 AC 于 E，交 AD 于 F，且 AEEF求证：ACBF 26如图（1）AB8cm，ACAB，BDAB，ACBD6cm点 P 在线段 AB 上以 2cm/s 的速度由点 A 向点 B 运动，同时，点 Q 在线段 BD 上由点 B 向点 D 运动它们运动的时间为 t（s） （1）若点 Q 的运动速度与点 P 的运动速度相等，当 t1 时，ACP 与BPQ 是否全等，请说明理由，并判断此时线段 PC 和线段 PQ 的位置关系； （2）如图（2） ，将
10、图（1）中的“ACAB，BDAB”改为“CABDBA60” ，其他条件不变设点 Q 的运动速度为 xcm/s， 是否存在实数 x， 使得ACP 与BPQ 全等？若存在， 求出相应的 x、 t 的值；若不存在，请说明理由 参考答案参考答案 一选择题一选择题 1解：如图， 在ABC 与EDF 中， ， ABCEDF（SAS） ， 1ABC ABC+2180， 1+2180 故选：D 2解：BACDAE， BADCAE， 在BAD 和CAE 中， ， BADCAE（SAS） ， 1ABD， 125，235， 32+ABD60， 故选：C 3解：AB2AC，点 D 是线段 AB 的中点， BDADAC
11、， ADE 为等腰直角三角形， EADEDA45，EAED， EACEAD+BAC45+90135，EDB180EDA18045135， EACEDB， 在ACE 和DBE 中， ， ACEDBE（SAS） ，所以正确； AECDEB， BECBED+DECAEC+DECDEA90， BEEC，所以正确； DEF90BED 而AECDEB， DEF90AEC， DFEAFC90ACE， 而 ACADAE， AECACE， DEFDFE， DEDF，所以错误； ACEDBE， SACESDBE， BDAD， SDAESDBE， SACESDAE， SDEFSACF，所以正确 故选：C 4解：如图
12、，12110， 18011802， ADC1801，AEB1802， ADCAEB， 在ACD 和ABE 中， ， ACDABE（SAS） ， CADBAE60， C1CAD1106050， CAE1802C1801105020， CAE 的度数为 20， 故选：D 5解：ADl，CEl， ADBBEC90， ABC90， ABD+EBCBCE+EBC90，即ABDBCE， 在ABD 和BEC 中， ， ABDBCE（AAS） ， BDCE，故正确； BAD+ABD90，ABDBCE， BAD+BCE90， 即BAD 与BCE 互余，故正确； ABDBCE， ADEB，DBCE， BE+DDE
13、， AD+CEDE，故正确 故选：D 6解：AD，BE 是ABC 的高线， ADBADCAEB90， BFDAFE， DBFCAD， 在ACD 和BFD 中， ， ACDBFD（ASA） ， DFDC， ACD 的面积为 12， ， CD4， DF4， AFADDF2， 故选：C 7解：第一块，仅保留了原三角形的一个角和部分边，不符合任何判定方法； 第二块，仅保留了原三角形的一部分边，所以该块不行； 第三块，不但保留了原三角形的两个角还保留了其中一个边，所以符合 ASA 判定，所以应该拿这块去 故选：C 8解：过点 A 作 AHBC 于 H，如图所示： 在ABC 与ADE 中， ， ABCAD
14、E（SAS） ， ADAB，SABCSAED， 又AFDE， DEAFBCAH， AFAH， AFDE，AHBC， AFGAHG90， 在 RtAFG 和 RtAHG 中， ， RtAFGRtAHG（HL） ， 同理：RtADFRtABH（HL） ， S四边形DGBAS四边形AFGH12， RtAFGRtAHG， SRtAFG6， AF4， FG46， 解得：FG3； 故选：C 9解：在ABE 和BCD 中， ， ABEBCD（SAS） ， BAECBD， BAE21，C28， CBD21， BDFCBD+C21+2849， BFAC， BFD90， FBD90BDF904941 故选：C 1
15、0解：H 是高 MQ 和 NR 的交点， P+PMQ90，PMQRHM90，QHN+HNQ90， RHMQHN， PQHN， 在PMQ 与HNQ 中， ， PMQHNQ（AAS） ， PQHQ，MQQN， MH3，PQ2， MQNQMH+HQMH+PQ3+25， PNPQ+QN2+57， 故选：B 二填空题二填空题 11解：ABAC， BC， 在BDF 和CED 中， ， BDFCDE（SAS） ， EDCDFB， EDFB（180A）290A， FDE， A1802， 故答案为： （1802） 12解：由题意可知ABCEDC， 3BAC， 又1+BAC90， 1+390， DFDC， 245
16、， 1+2+3135 度， 故答案为：135 13解：B+BAE90，C+CAF90，BC 12（正确） EF90，BC，AEAF ABEACF（ASA） ABAC，BECF（正确） CANBAM，BC，ABAC ACNABM（正确） CNBM（不正确） 所以正确结论有 故填 14解：在ADB 和CBE 中， ， ADBCBE（SAS） ， 14，26，DBBE， 1+2+A180，2+3+4180，A56， 3A56， 在DBE 中，DBBE， BDE5（1803）262， 故答案为：62 15解：延长 AP 交 BC 于 E， AP 垂直B 的平分线 BP 于 P， ABPEBP， 又BP
17、BP，APBBPE90， ABPBEP（ASA） ， SABPSBEP，APPE， APC 和CPE 等底同高， SAPCSPCE， SPBCSPBE+SPCESABC5cm2， 故答案为：5 16解：EAF+BAG90，EAF+AEF90， BAGAEF， 在AEF 和BAG 中， AEFBAG， （AAS） 同理BCGCDH， AFBG，AGEF，GCDH，BGCH， 梯形 DEFH 的面积（EF+DH） FH80， SAEFSABGAFAE9， SBCGSCDHCHDH6， 图中实线所围成的图形的面积 S80292650， 故答案为：50 17解：AABC， AABABC70， ABCA
18、BC， BABA，ABCABC70， AABAAB70， ABA40， ABC30， CBC40， 故答案为：40 三解答题三解答题 18证明：在 AB 上取一点 F，使 AFAC，连接 EF EA、EB 分别平分CAB 和DBA， CAEFAE，EBFEBD ACBD， C+D180 在ACE 和AFE 中， ， ACEAFE（SAS） ， CAFE AFE+EFB180， EFBD 在BEF 和BED 中， ， BEFBED（AAS） ， BFBD ABAF+BF， ABAC+BD 19 （1）证明：作 CFAD，交 AD 延长线与 F CDF+ADC180 ABC+ADC180 CDFA
19、BC，即EBCCDF CEAB，那么CEBCFD90 在CFD 和CEB 中， ， CDFCBE（AAS） CECF CFAD，CEAB，CECF， AC 平分BAD； （2）解：AC 平分BAD FACEAC 在CFA 和CEA 中， ， CFACEA（AAS） ， AFAE9， CDFCBE， DFBE3， ADAFFD936 20 （1）证明：AC 平分BAD，CEAB，CFAD CECF ABC+D180，ABC+EBC180 EBCD CEBCFD90 CBECDF （2）证明：CECF，ACAC ACEACF AEAF AB+DFAB+BEAEAF 21解：BFBG，BFBG，理由
20、如下： AD，CE 是高， BAD+AFEBCF+CFD90， AFECFD， BADBCF， 在ABG 与CFB 中， ， ABGCFB（SAS） ， BFBG； ABGCFB， GFBD， ADBC， BDG90 G+DBG90， FBD+DBG90， FBG 的度数为 90， BFBG 22 （1）证明：BGAC， CGBD， D 是 BC 的中点， BDDC， 在CFD 和BGD 中 ， CFDBGD， BGCF （2）BE+CFEF， 理由如下： CFDBGD， CFBG， 在BGE 中，BG+BEEG， CFDBGD， GDDF，EDGF， EFEG， BE+CFEF 23解： （
21、1）DFCD，CDDF 理由：AFAB， DAF90， 在ADF 和BCD 中， ， ADFBCD（SAS） ， DFCD，ADFBCD， BCD+CDB90， ADF+CDB90，即CDF90， CDDF （2）成立，理由如下： AFAB， DAF90， 在ADF 和BCD 中， ， ADFBCD（SAS） ， DFCD，ADFBCD， BCD+CDB90， ADF+CDB90，即CDF90， CDDF 24 （1）证明：BEEA，CFAF， BACBEACFE90， EAB+CAF90，EBA+EAB90， CAFEBA， 在ABE 和AFC 中， BEAAFC90，EBACAF，ABAC
22、， BEAAFC（AAS） EAFC，BEAF EFEB+CF （2）解：BEEA，CFAF， BACBEACFE90， EAB+CAF90，ABE+EAB90， CAFABE， 在ABE 和AFC 中， BEAAFC90，EBACAF，ABAC， BEAAFC（AAS） EAFC3，BEAF10 EFAFCF1037 25 （1）解：在ADC 和EDB 中 ， ADCEDB（SAS） ， 故选 B； （2）解：由（1）知：ADCEDB， BEAC6，AE2AD， 在ABE 中，AB8，由三角形三边关系定理得：862AD8+6， 1AD7， 故选 C （3）证明： 延长 AD 到 M，使 AD
23、DM，连接 BM， AD 是ABC 中线， CDBD， 在ADC 和MDB 中 ADCMDB， BMAC，CADM， AEEF， CADAFE， AFEBFD， BFDCADM， BFBMAC， 即 ACBF 26解： （1）ACPBPQ， ACAB，BDAB AB90 APBQ2 BP6 BPAC， 在ACP 和BPQ 中， ， ACPBPQ， CQPB， APC+C90， APC+QPB90， PCPQ； （2）存在 x 的值，使得ACP 与BPQ 全等， 若ACPBPQ， 则 ACBP，APBQ，可得：682t，2txt 解得：x2，t1； 若ACPBQP， 则 ACBQ，APBP，可得：6xt，2t82t 解得：x3，t2；
