1、 第第 2 章解直角三角形章解直角三角形 一选择题（共一选择题（共 10 小题，满分小题，满分 30 分）分） 1已知：cos，则 范围是（ ） A030 B3045 C45a60 D60a90 2x 为锐角，则 cosx 的值为（ ） A B C D 3王明同学遇到了这样一道题，则锐角 的度数为（ ） A40 B30 C20 D10 4在 RtABC 中，C90，AB5，AC4下列四个选项，正确的是（ ） AtanB0.75 BsinB0.6 CsinB0.8 DcosB0.8 5已知cosAsin80，则锐角 A 的取值范围是（ ） A60A80 B30A80 C10A60 D10A30
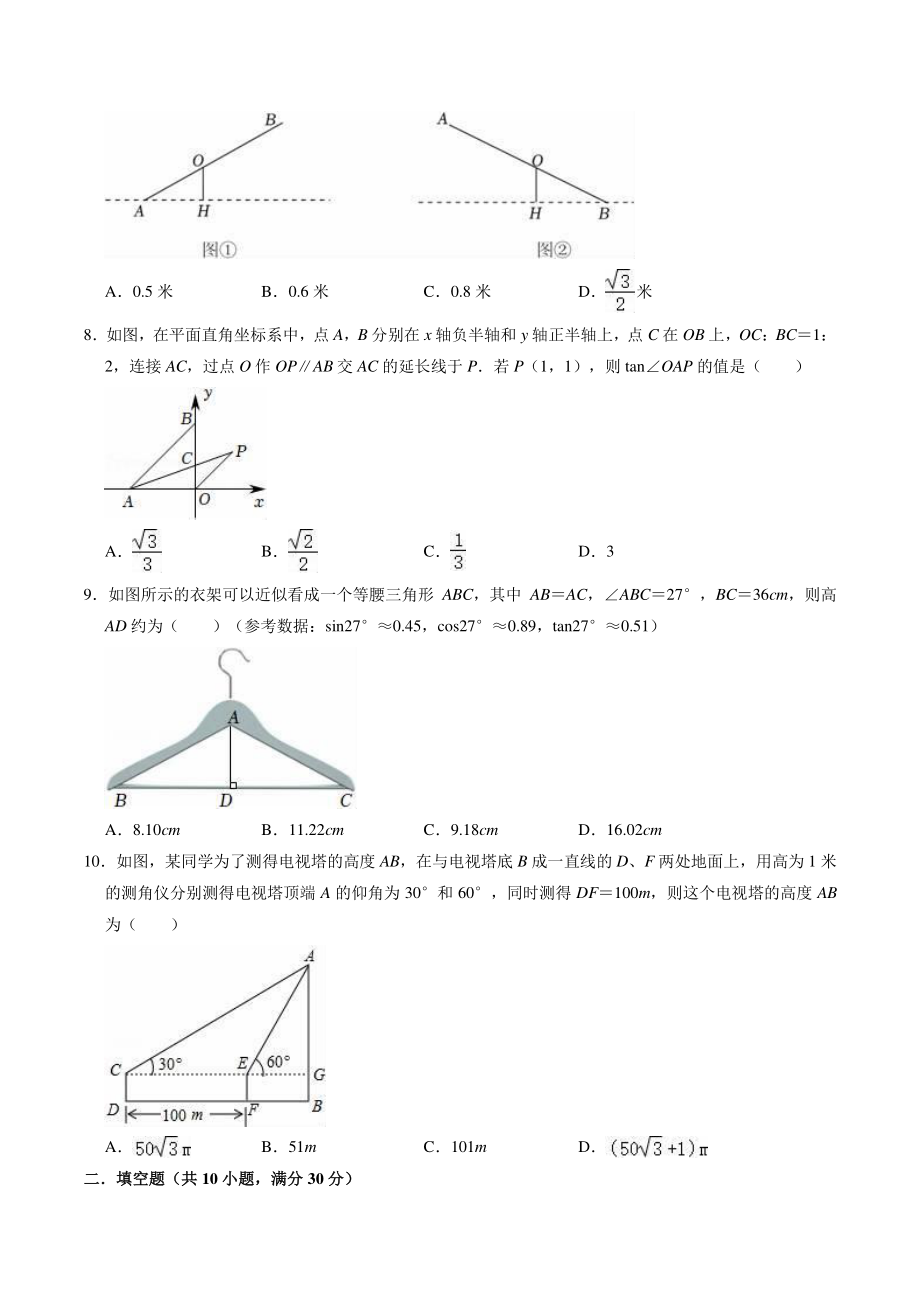
2、6如图，某车型车门设计属于剪刀门设计，即车门关闭时位置如图中四边形 ABCD，车门打开是绕点 A 逆时针旋转至 CD 与 AD 垂直， 已知四边形 ABCD 与四边形 ABCD在同一平面， 若 ADBC， D45，DAB30，CD60cm，则 AB 的长约为（ ） A60cm B51cm C42cm D21cm 7如图所示是一个左右两侧不等长的跷跷板，跷板 AB 长为 4 米，支柱 OH 垂直地面如图，当 AB 的一端 A 接触地面时，AB 与地面的夹角的正弦值为；如图，当 AB 的另一端 B 接触地面时，AB 与地面的夹角的正弦值为，则支柱 OH 的长为（ ） A0.5 米 B0.6 米 C
3、0.8 米 D米 8如图，在平面直角坐标系中，点 A，B 分别在 x 轴负半轴和 y 轴正半轴上，点 C 在 OB 上，OC：BC1：2，连接 AC，过点 O 作 OPAB 交 AC 的延长线于 P若 P（1，1），则 tanOAP 的值是（ ） A B C D3 9如图所示的衣架可以近似看成一个等腰三角形 ABC，其中 ABAC，ABC27，BC36cm，则高AD 约为（ ）（参考数据：sin270.45，cos270.89，tan270.51） A8.10cm B11.22cm C9.18cm D16.02cm 10如图，某同学为了测得电视塔的高度 AB，在与电视塔底 B 成一直线的 D、
4、F 两处地面上，用高为 1 米的测角仪分别测得电视塔顶端 A 的仰角为 30和 60，同时测得 DF100m，则这个电视塔的高度 AB为（ ） A B51m C101m D 二填空题（共二填空题（共 10 小题，满分小题，满分 30 分）分） 11若A 为锐角，且 cosA，则A 的取值范围是 12如图所示的网格是正方形网格，点 A，B，P 是网格线交点，则 tanPAB+tanPBA 13请从以下两个小题中任选一个作答，若多选，则按第一题计分 A正七边形的对称轴有 条 B用科学计算器计算： （结果精确到 0.01） 14若 sin（x20），则 x 15在 RtABC 中，B90，AC200
5、，sinA0.6，则 BC 16已知A 是锐角 tanA，则 sinA 17 是锐角，若 sincos15，则 18一艘船向正北方向航行，在 A 处时看到灯塔 S 在船的北偏东 30的方向上，继续航行 12 海里到达 B处，看到灯塔 S 在船的北偏东 60的方向上若继续沿正北方向航行，航行过程中船距灯塔 S 的最近距离为 海里（结果精确到 0.1 海里）（参考数据：1.41，1.73） 19一名滑雪运动员沿着坡比为的滑道下滑，已知该运动员滑行距离为 1000 米，则高度下降了 米 20小明用一块含有 60角（DAE60）的直角三角尺测量校园内某棵树的高度，示意图如图所示若小明的眼睛与地面之间的
6、垂直高度 AB 为 1.60m，小明与树之间的水平距离 BC 为 4m，则这棵树的高度约为 m（结果精确到 0.1m，参考数据：1.70） 三解答题（共三解答题（共 7 小题，满分小题，满分 90 分）分） 21已知如图，A，B，C，D 四点的坐标分别是（3，0），（0，4），（12，0），（0，9），探索OBA和OCD 的大小关系，并说明理由 22先化简，再求值：（a），其中 a2sin45+（）1 23如图，在四边形 ABCD 中，B90，AB2，CD8连接 AC，ACCD如果 sinACB，求AD 的长 24在ABC 中，C90，sinA，AB25，求ABC 的周长和 tanA 的值 2
7、5用计算器求下列各式的值： （1）sin47； （2）sin1230； （3）cos2518； （4）tan445959； （5）sin18+cos55tan59 26如图是一座人行天桥的引桥部分的示意图，上桥通道由两段互相平行并且与地面成 37角的楼梯 AD、BE 和一段水平平台 DE 构成已知天桥高度 BC4.5 米，引桥水平跨度 AC8 米 （参考数据：取 sin370.60，cos370.80，tan370.75） （1）求水平平台 DE 的长度； （2）若与地面垂直的平台立柱 MN 的高度为 3 米，求两段楼梯 AD 与 BE 的长度之比 27在ABC 中，已知C90，sinA+si
8、nB，求 sinAsinB 的值 参考答案解析参考答案解析 一选择题（共一选择题（共 10 小题，满分小题，满分 30 分）分） 1解：cos300.866，cos450.707，cos600.5， 锐角的余弦值随着角度的增大而减小，cos0.67， 4560 故选：C 2解：sin2x+cos2x1， cosx 故选：B 3解：tan30， tan301， tan（+10）1， +1030， 20， 故选：C 4解：如图，C90，AB5，AC4， BC3， A 选项，原式，故该选项不符合题意； B 选项，原式0.8，故该选项不符合题意； C 选项，原式0.8，故该选项符合题意； D 选项，原
9、式0.6，故该选项不符合题意； 故选：C 5解：cos60，sin80cos10， cos60cosAcos10， 10A60 故选：C 6解：设 AD 与 BC交于 G， 过 B作 BFAD 于 F，延长 DC交 AD 于 E， 由旋转的性质得，DD45，ABAB，CDCD60cm， DCAD， AED90， AED是等腰直角三角形， AEDE， ADBC， ADBC， GCE 是等腰直角三角形， CEGE， AGCD60， FGBCGE45， FGFB， DAB30， AFFB， FB+FB60， FB30（1）， ABAB2FB60（1）42cm 故选：C 7解：在 RtAOH 中，si
10、nA， OA2OH， 同理可得：OB3OH， AB4 米， 2OH+3OH4， 解得：OH0.8， 故选：C 8解：如图，过点 P 作 PQx 轴于点 Q， OPAB， CABCPO，ABCCOP， OCPBCA， CP：ACOC：BC1：2， AOCAQP90， COPQ， OQ：AOCP：AC1：2， P（1，1）， PQOQ1， AO2， tanOAP 故选：C 9解：ABAC，ADBC，BC36cm， BDBC18cm 在 RtABD 中， tanABC，ABC27， ADtanABCBD 0.5118 9.18（cm） 故选：C 10解：由题意得： ACE30，AEG60，CDEFG
11、B1 米，CEDF100 米， AEG 是ACE 的一个外角， CAEAEGACE30， CAEACE30， AECE100 米， 在 RtAEG 中，AGAEsin6010050（米）， ABAG+BG（50+1）米， 故选：D 二填空题（共二填空题（共 10 小题，满分小题，满分 30 分）分） 11解：0， 又 cos60，cos900，锐角余弦函数值随角度的增大而减小， 当 cosA时，60A90 故答案为：60A90 12解：设小正方形的边长是 a， tanPAB， tanPBA， tanPAB+tanPBA+ 13解：A、正七边形的对称轴有 7 条， 故答案为：7； B、4.796
12、0.9814.70， 故答案为：4.70 14解：sin（x20）， x2060， x80， 故答案为：80 15解：在 RtABC 中，B90，AC200，sinA0.6， BCACsinA2000.6120， 故答案为：120 16解：tanA， 设A 的对边为a，则邻边为 2a， 斜边长a， sinA， 故答案为： 17解：sincos15， 901575 故答案为：75 18解：过点 S 作 SCAB，交 AB 的延长线于点 C， 由题意得，BAS30，AB12 海里，CBS60， 设 BCx 海里，则 AC（x+12）海里， 在 RtBCS 中，tan60， 解得 CSx， 在 Rt
13、ACS 中，tan30， 解得 x6， CS10.4 海里， 即航行过程中船距灯塔 S 的最近距离为 10.4 海里 故答案为：10.4 19解：如图所示，ABC 中，AB：BC1：，B90，AC1000， AB2+BC2AC2， AB2+3AB210002， AB500 米， 高度下降了 500 米， 故答案为：500 20解：ABBC，DCBC，ADBC， 四边形 ABCD 是矩形， BC4m，AB1.60m， ADBC4m，DCAB1.60m， 在 RtAED 中， DAE60，AD4m， EDADtan6044（m）， CEED+DC4+1.608.4（m） 答：这棵树的高度约为 8.
14、4m 故答案为：8.4 三解答题（共三解答题（共 7 小题，满分小题，满分 90 分）分） 21解：OBAOCD，理由如下： 由勾股定理，得 AB5，CD15， sinOBA，sinOCD， OBAOCD 22解：（a） ， a2sin45+（）1 2+2 ， 代入得：原式 23解：B90，AB2，sinACB， AC6， ACCD， ACD90， CD8， AD10， AD 的长为 10 24解：在ABC 中，C90，sinA，AB25， sinA BCAC20 在ABC 中，C90，15 tanA ABC 的周长为 AB+BC+AC25+20+1560 25解：根据题意用计算器求出： （1
15、）sin470.7314； （2）sin12300.2164； （3）cos25180.9003； （4）tan4459591.0000； （5）sin18+cos55tan590.7817 26解：（1）如图，延长 BE 交 AC 于点 F 由题意可知 DE/AC，AD/BF， 四边形 AFED 是平行四边形 DEAF 在 RtBFC 中，即， （米）， DEAFACFC862（米） 答：水平平台 DE 的长度为 2 米 （2）如图，延长 DE 交 BC 于点 G，作 DHAC 于点 H 由题意知DAHBEG37，BGEDHA90， DAHBEG， DHCGMN3，BC4.5， ， AD：BE2：1 答：两段楼梯 AD 与 BE 的长度之比为 2：1 27解：sinA+sinB， （sinA+sinB）2， sin2A+sin2B+2sinAsinB， sinBcosA， sin2A+cos2A+2sinAsinB， 2sinAsinB， （sinAsinB）21， sinAsinB
