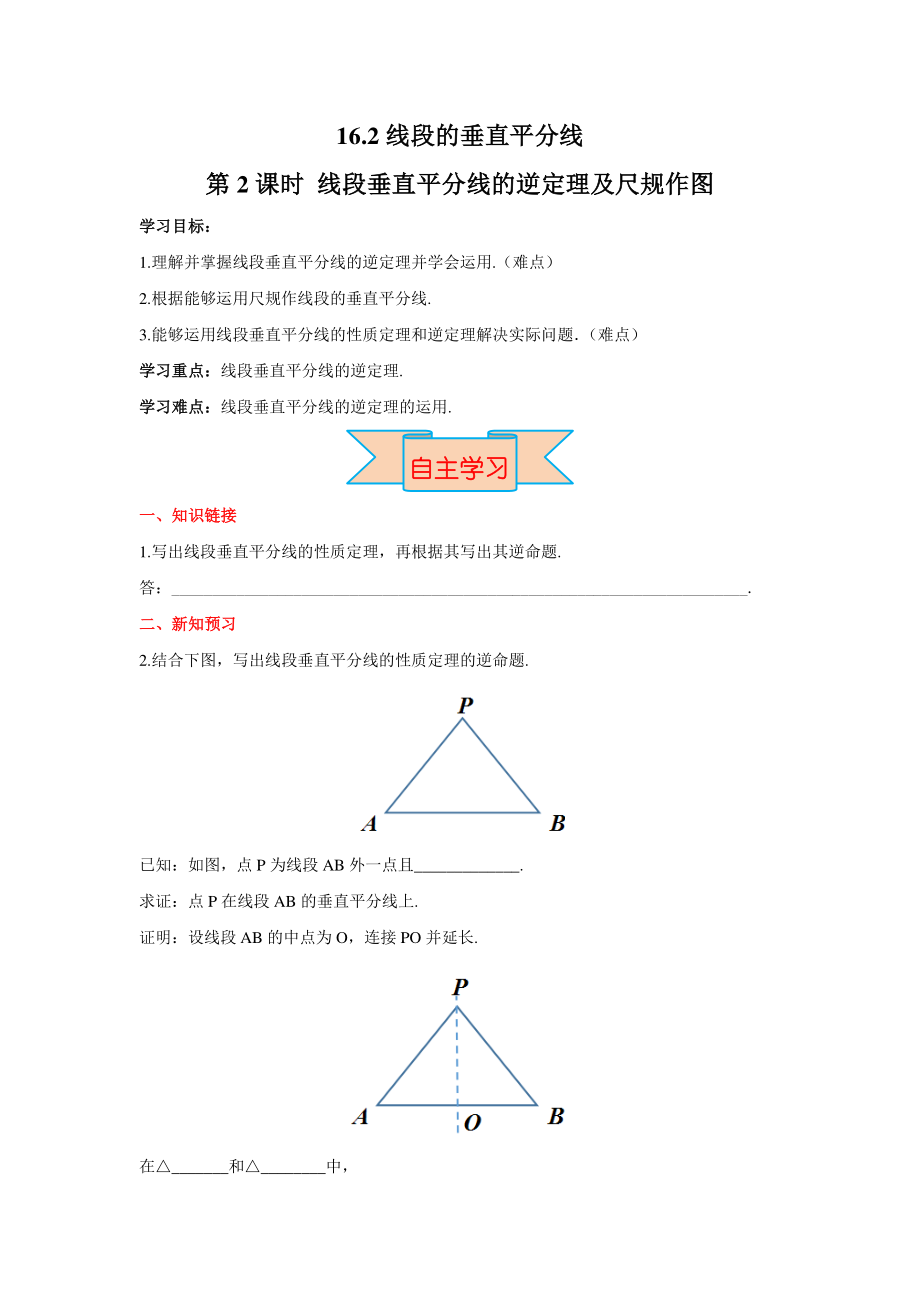
1、16.2 线段的垂直平分线线段的垂直平分线 第第 2 课时课时 线段垂直平分线的逆定理及尺规作图线段垂直平分线的逆定理及尺规作图 学习目标：学习目标： 1.理解并掌握线段垂直平分线的逆定理并学会运用.（难点） 2.根据能够运用尺规作线段的垂直平分线. 3.能够运用线段垂直平分线的性质定理和逆定理解决实际问题 （难点） 学习重点：学习重点：线段垂直平分线的逆定理. 学习难点：学习难点：线段垂直平分线的逆定理的运用. 一、一、知识链接知识链接 1.写出线段垂直平分线的性质定理，再根据其写出其逆命题. 答：_. 二、二、新知预习新知预习 2.结合下图，写出线段垂直平分线的性质定理的逆命题. 已知：如
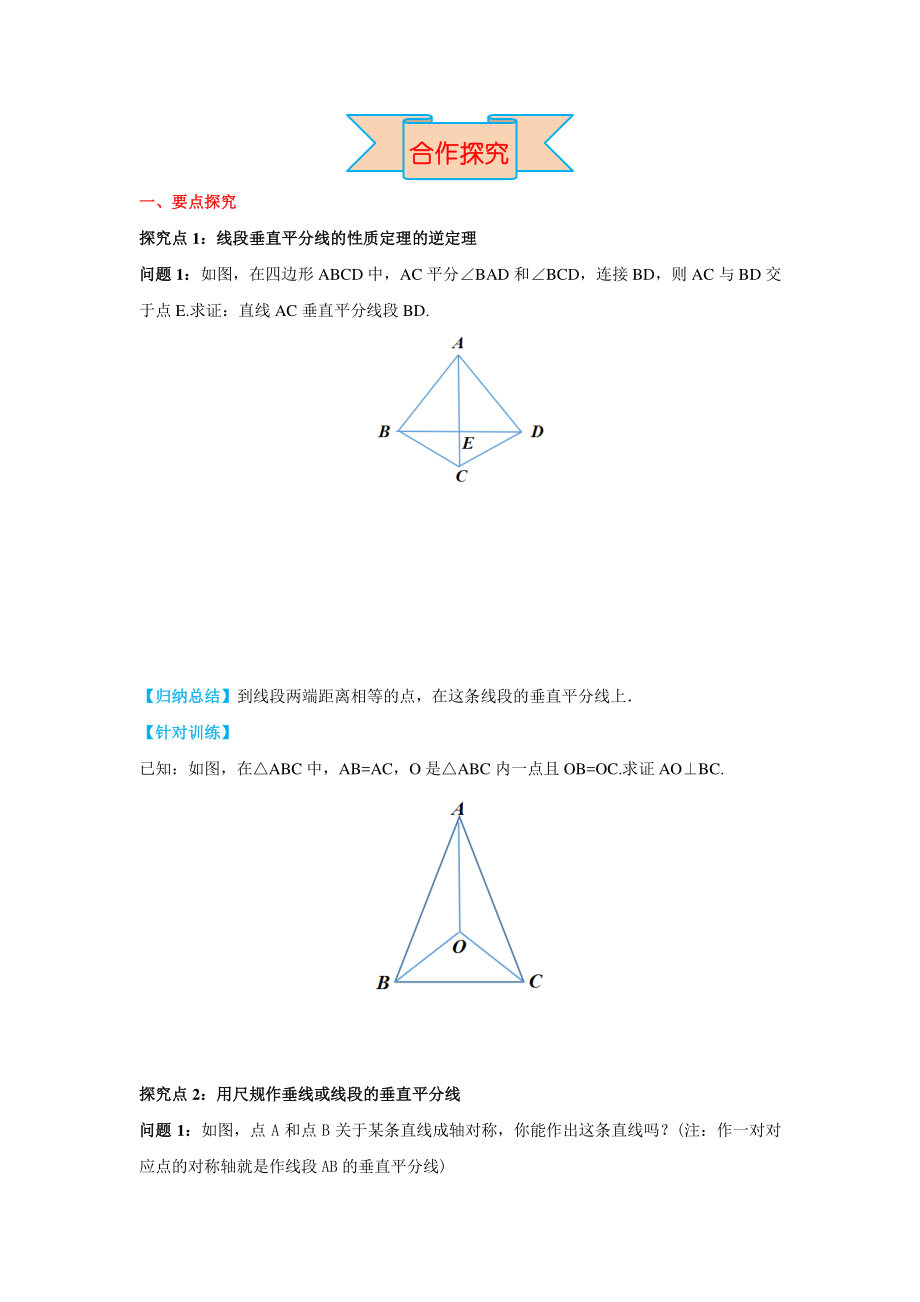
2、图，点 P 为线段 AB 外一点且_. 求证：点 P 在线段 AB 的垂直平分线上. 证明：设线段 AB 的中点为 O，连接 PO 并延长. 在_和_中， 自主学习自主学习 _, _. _. _. _. _. _. 于是我们得到线段垂直平分线性质定理的逆定理线段垂直平分线性质定理的逆定理： 到线段两个端点距离相等的点，在这条线段的_上 三、自学自测三、自学自测 1 在锐角 ABC 内一点 P 满足 PA=PB=PC，则点 P 是 ABC（ ） A三条角平分线的交点 B三条中线的交点 C三条高的交点 D三边垂直平分线的交点 2、如图 1，四边形 ABCD，AB=AD，BC=DC， 则 AC 与
3、BD 的位置关系是 ， 点 A 在线段 BD 的 上， 点 C 在线段 BD 的 上. 3、如图 2，AD 是 ABC 的高，E 为 AD 上一点，且 BE=CE， 则 ABC 为 三角形。 四、我的疑惑四、我的疑惑 _ _ _ _ _ A B C D 图 1 A B C D E 图 2 一、一、要点探究要点探究 探究点探究点 1：线段垂直平分线的性质定理的逆定理线段垂直平分线的性质定理的逆定理 问题问题 1：如图，在四边形 ABCD 中，AC 平分BAD 和BCD，连接 BD，则 AC 与 BD 交于点 E.求证：直线 AC 垂直平分线段 BD. 【归纳总结】【归纳总结】到线段两端距离相等的
4、点，在这条线段的垂直平分线上 【针对训练】【针对训练】 已知：如图，在ABC 中，AB=AC，O 是ABC 内一点且 OB=OC.求证 AOBC. 探究点探究点 2：用尺规作垂线或线段的垂直平分线用尺规作垂线或线段的垂直平分线 问题问题 1：如图，点 A 和点 B 关于某条直线成轴对称，你能作出这条直线吗？(注：作一对对应点的对称轴就是作线段 AB 的垂直平分线) 合作探究合作探究 【归纳总结】【归纳总结】要熟练掌握线段垂直平分线的作法，作出的图形中的作图痕迹要保留 问题问题 2：如图，已知ABC，用尺规求作ACB 的中线 CD. 【归纳总结】【归纳总结】要熟练掌握线段垂直平分线的作法，作出的
5、图形中的作图痕迹要保留 【针对训练】【针对训练】 已知ABC 中，试画出三边的垂直平分线. 二、课堂小结二、课堂小结 内容 线段的垂直平分线性质的逆定理 与一条线段两个端点距离相等的点，在这条线段的_上 直线 l 是线段 AB 的垂直平分线，P 为 l 上一点，则 PAPB；反过来，若 PAPB，则点 P 在线段 AB 的垂直平分线上. 用尺规作垂线或线段的垂直平分线 A，B 两点关于某直线对称，则连接 AB，分别以 A，B 为圆心，大于12AB 的长为半径画弧，两弧相交于 E、F 两点，作直线 EF，则 EF 就是其垂直平分线. 1.如图所示，AC=AD,BC=BD,则下列说法正确的是（ ） AAB 垂直平分 CD； B CD 垂直平分 AB ； CAB 与 CD 互相垂直平分； DCD 平分 ACB 2.已知线段 AB，在平面上找到三个点 D、E、F，使 DADB，EAEB,FAFB，这样的点的组合共有_种. 3.如图，点 D 在ABC 的边 BC 上且 BC=BD+AD，则点 D 在线段_垂直平分线上. 4.如图，ABC 和ABC关于直线 l 对称，请用无刻度的直尺作出它们的对称轴. 当堂检测参考答案：当堂检测参考答案： 当堂检测当堂检测 1.A 2.无数 3.AC 4. .
