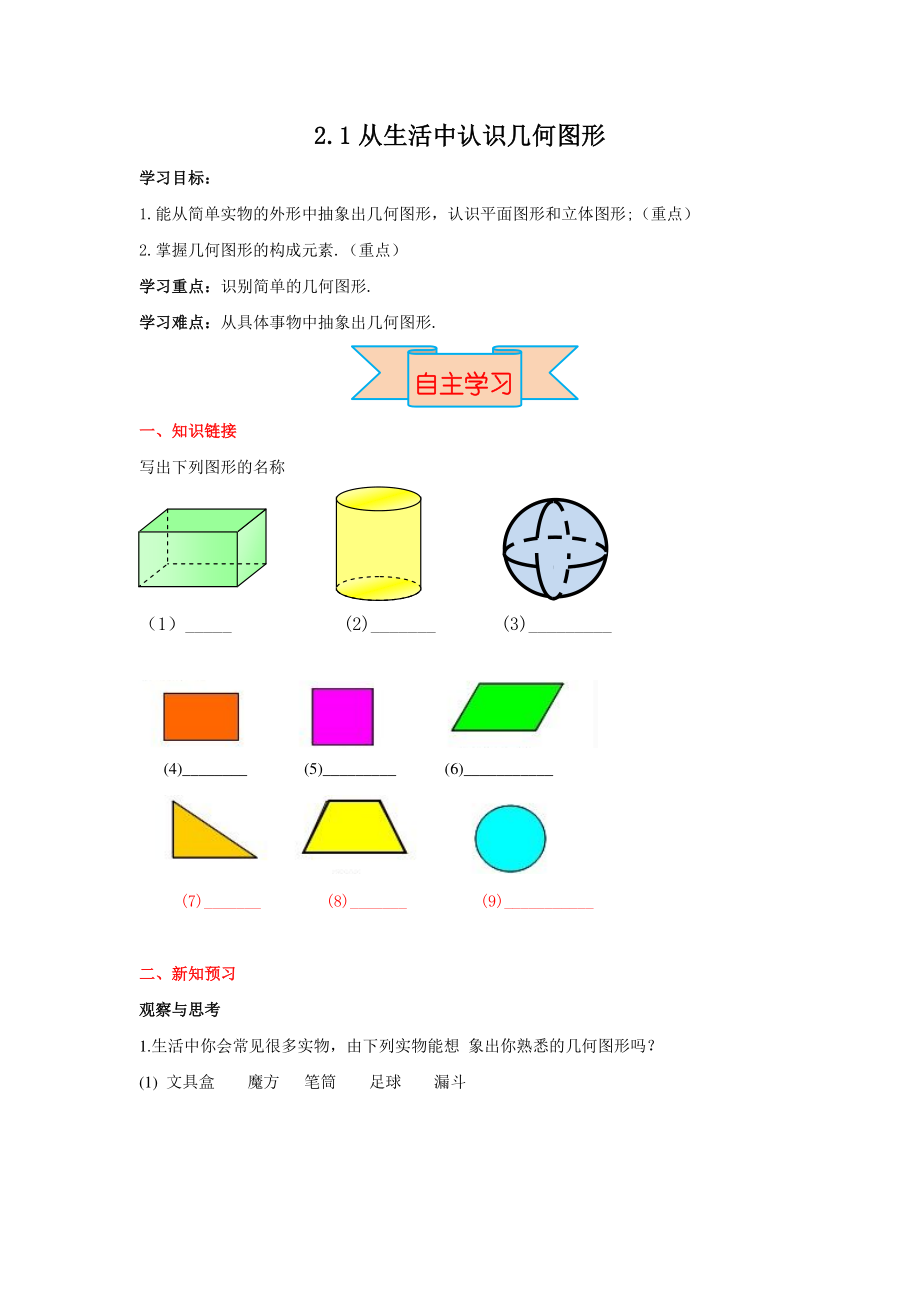
1、2.12.1 从生活中认识几何图形从生活中认识几何图形 学习目标：学习目标： 1.能从简单实物的外形中抽象出几何图形，认识平面图形和立体图形;（重点） 2.掌握几何图形的构成元素.（重点） 学习重点：学习重点：识别简单的几何图形. 学习难点：学习难点：从具体事物中抽象出几何图形. 一、一、知识链接知识链接 写出下列图形的名称 （1）_ (2)_ (3)_ (4)_ (5)_ (6)_ (7)_ (8)_ (9)_ 二、二、新新知预习知预习 观察与思考观察与思考 1.生活中你会常见很多实物，由下列实物能想 象出你熟悉的几何图形吗？ (1) 文具盒 魔方 笔筒 足球 漏斗 自主学习自主学习 (2)
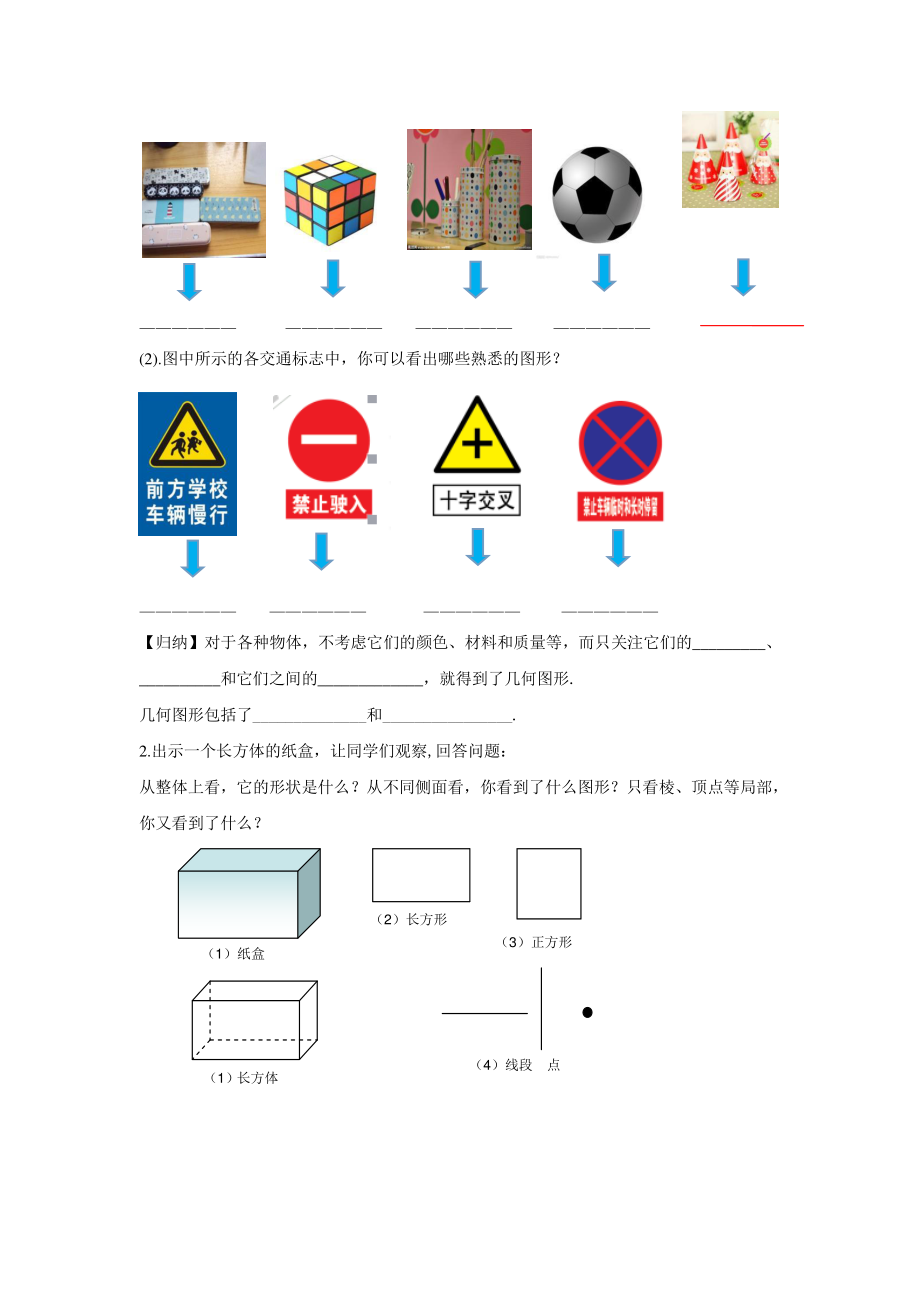
2、.图中所示的各交通标志中，你可以看出哪些熟悉的图形？ 【归纳】对于各种物体，不考虑它们的颜色、材料和质量等，而只关注它们的_、_和它们之间的_，就得到了几何图形. 几何图形包括了_和_. 2.出示一个长方体的纸盒，让同学们观察,回答问题： 从整体上看，它的形状是什么？从不同侧面看，你看到了什么图形？只看棱、顶点等局部，你又看到了什么？ （1）纸盒 （1）长方体 （2）长方形 （3）正方形 （4）线段 点 想一想：圆柱和球从整体上看，它的形状是什么？从不同侧面看，你看到了什么图形？ 【归纳】 包围着几何体的是_;面分_和_; 面与面相交成_; 线与线相交成_. _、_、_是几何图形的基本要素.
3、三、三、自学自测自学自测 请把下面的实物与相应的几何体用线连接起来： 四、我的疑惑四、我的疑惑 _ _ _ _ _ 一、一、要点探究要点探究 探究点探究点 1：几何图形的分类几何图形的分类 例例 1 1：下列几种图形：长方形；梯形；正方体；圆柱；圆锥；球. 其中属于立体图形的是（ ） A. ；B. ；C. ；D. 【归纳总结】【归纳总结】 立体图形的各部分不都在同一平面内， 而平面图形的各部分都在同一平面内；立体图形中某些部分是平面图形. 例例 2：将如图所示的几何体分类： 【归纳总结】【归纳总结】 生活中常见的几何体有两种分类：一种是按柱体、椎体、球体分类；一种是按平面、曲面分类. 【针对训
4、练】【针对训练】 观察图中的立体图形，分别写出它们的名称,并将它们分类. _ 探究点探究点 2：几何图形的构成元素几何图形的构成元素 合作探究合作探究 1.包围着几何体的是面面分为_和_两种 如图的圆锥体有两个面，一个是平面，另一个是曲面 如图的六棱柱有_个面，分别都是什么面？ 合作探究合作探究 如图的圆柱有_个面，分别都是什么面？ 2.面与面相交的地方形成线线分为_和_两种 圆锥体的两个面相交形成_线 六棱柱的两个面相交成_线. 3.线与线相交形成点 想一想 （1）如果把笔尖可能看作一个点，笔尖在纸上运动会形成什么_ 如果把星星看作一个点，夜空中流星形成什么_ （2）我们可以把汽车的雨刷看成
5、一条线，汽车的雨刷在挡风玻璃上运动形成_ 由此我们可以得出：点动成_，线动成_ :例例 3：如图所示，将平面图形绕轴旋转一周，得到的几何体是( ) 【归纳总结】【归纳总结】点动成线，线动成面，面动成体，以运动的观点观察静止的点、线、面，就能得到千姿百态的几何图形解答此题可动手操作，也可以空间想象 【针对训练】【针对训练】 将下列图形绕直线 l 旋转一周, 可以得到右图所示的立体图形的是( ) 二、课堂小结二、课堂小结 内容 几何图形 几何图形包括立体图形和平面图形. 几何图形的构成元素 点、线、面是构成几何图形的基本要素. 1.圆锥的面有（ ） A. 1 个 B.2 个 C.3 个 D.无数多
6、个 2.将正方体、圆锥、球、四棱柱四种几何体分类正确的是（ ） .正方体、四棱柱是柱体，圆锥是锥体，球是球体； .正方体、圆锥、四棱柱都是柱体，球是球体； .圆锥、四棱柱是柱体一类，正方体的面是平面一类，球的面是曲面一类； .正方体、圆锥、球、四棱柱都是柱体。 .下列各图中，是柱体的为（ ） . . . . 4.如图所示，下列图形绕着虚线旋转一周得到圆锥体的是 ( ) 5.将一个直角三角形绕它的最长边(斜边)旋转一周得到的几何体是如图中的( ) 6.下列结论中正确的是( ) 圆柱由 3 个面围成，这 3 个面都是平面； 圆锥由 2 个面围成，这 2 个面中，1 个是平面，1 个是曲面； 球仅由
7、 1 个面围成，这个面是平面； 正方体由 6 个面围成，这 6 个面都是平面 A B C D 7.如图，左面是一些具体的物体，右面是一些立体图形，试找出与下面立体图形相类似的实物(用线连接) 当堂检测当堂检测 8.对于棱柱体而言，不同的棱柱体由不同的面构成： 三棱柱由 2 个底面，3 个侧面，共 5 个面构成； 四棱柱由 2 个底面，4 个侧面，共 6 个面构成； 五棱柱由 2 个底面，5 个侧面，共 7 个面构成； 六棱柱由 2 个底面，6 个侧面，共 8 个面构成； （1）根据以上规律判断，十二棱柱共有多少个面？ （2）若某个棱柱由 24 个面构成，那么这个棱柱是什么棱柱？ （3）棱柱底面多边形的边数为n，则侧面的个数为多少？棱柱共有多少个面？ （4）底面多边形边数为n的棱柱，其顶点个数为多少个？有多少条棱？ 当堂检测参考答案：当堂检测参考答案： 1.A 2.A 3.C 4.D 5.D 6.C 7.连线如下图所示： 8.(1) 14 (2) 二十二棱柱 （3）n n+2 (4) 2n n
