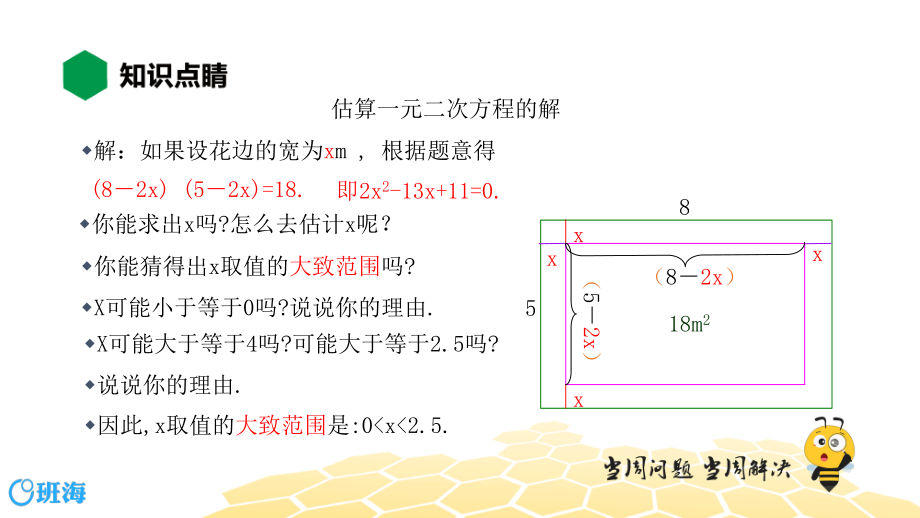
1、【知识精讲】一元二次方程的解的估算 初三 数学 一块四周镶有宽度相等的花边的地毯如下图，它的长为m，宽为m如果地毯中央长方形图案的面积为1m2 ，则花边多宽?如何解决这个问题呢?课海知识精讲课堂进一步探究，将会有新法推出。 估算一元二次方程的解 解：如果设花边的宽为xm , 根据题意得 你能求出x吗?怎么去估计x呢？ (82x) (52x)=18. 5 x x x x （82x） 8 18m2 即2x2-13x+11=0. 你能猜得出x取值的大致范围吗? X可能小于等于0吗?说说你的理由. X可能大于等于4吗?可能大于等于2.5吗? 说说你的理由. 因此,x取值的大致范围是:0 x2.5. 在
2、0 x2.5这个范围中,x具体的值=? 完成下表(取值计算,逐步逼近): 由此看出,可以使2x2-13x+11的值为0的x=1.故可知花边宽为1m. 你还有其它求解方法吗? 如果将(8-2x)(5-2x)=18看作是63=18. 则有8-2x=6, 5-2x=3.从而也可以解得x=1. 若在x许可的范围内取整数值，没有一个整数能够使方程的左边等 于0怎么办？ x 2x2-13x+11 0.5 1 1.5 2 4.75 0 -4 -7 如图，一个长为10m的梯子斜靠在墙上，梯子的顶端距地面的垂直距离为8m 如果梯子的顶端下滑1m，那么梯子的底端滑动多少米？ 解：如果设梯子底端滑动xm，根据题意得
3、 你能猜得出x取值的大致范围吗? 72+(x+6)2=102 数学化 xm 8m 7m 6m 1m 即 x2+12x-15=0 由勾股定理可知x取值的大致范围是:1x1.5 如果x取整数是几?如果x精确到十分位呢?百分位呢? 在1x1.5这个范围中,如果x取整数是几?如果x精确到十分位呢?百分位呢? 完成下表(取值计算,逐步逼近): 由此看出,可以使x2+12x-15的值接近于0的x为整数的值是x=1;精确到十分位的x的值约是1.1. x x2+12x-15 0.5 1 1.5 2 -8.75 -2 5.25 13 x x2+12x-15 1.1 1.2 1.3 1.4 -0.59 0.84
4、2.29 3.76 总结用估算法解一元二次方程步骤总结用估算法解一元二次方程步骤： 第一步第一步：化为一般：化为一般形式形式 axax2 2 + +bx+cbx+c=0=0 第二步第二步：根据实际情况确定：根据实际情况确定x x大体的取值范围。大体的取值范围。 第三步第三步: :在在x x范围内取整数值范围内取整数值, ,能够使方程左边等于能够使方程左边等于0,0,则这个数则这个数就就 是是方程的一个解方程的一个解. . 第四步第四步：若在：若在x x的范围内取值，没有一个数的范围内取值，没有一个数能够使能够使方程的左边等于方程的左边等于0, 0, 则则找出值最接近于找出值最接近于0 0且小于且小于0 0的数，这个数就是的数，这个数就是方程解的方程解的近似取值。近似取值。 根据题意,列出方程,并估算方程的解： 1.一面积为120m2的矩形苗圃，它的长比宽多2m，苗圃的长和宽各是多少？ 解：设矩形的宽为xm，则长为(x2) m, 根据题意得： x(x2)120. 即 x22x1200. x x+2 120m2 根据题意,x的取值范围大致是0 x11. 完成下表(在0 x11这个范围内取值计算,逐步逼近): 由此看出,可以使x2+2x-120的值为0的x=10.故可知宽为10m,长为12m. x X2+2x-120 8 9 10 11 -40 -21 0 23
