1、2020-2021 学年四川省成都市成华区七年级学年四川省成都市成华区七年级下期末数学试卷下期末数学试卷 一、选择题（本大题共一、选择题（本大题共 10 个小题，每小题个小题，每小题 3 分，共分，共 30分）分） 1. 汽车以每小时 100 千米的速度匀速行驶，行驶的路程随时间的变化而变化，在这个变化过程中，自变量是（ ） A 汽车 B. 路程 C. 速度 D. 时间 2. 下列四个图形中，不是轴对称图形的是（ ） A. B. C. D. 3. 肥皂泡的泡壁厚度大约是 0.00000071米，数字 0.00000071用科学记数法表示为（ ） A. 7.1 109 B. 7.1 108 C.
2、 7.1 107 D. 7.1 106 4. 下列计算正确是（ ） A. （a2）4a8 B. a2a4a8 C. （a+b）2a2+b2 D. a2+a2a4 5. 下列事件中，不是必然事件是（ ） A. 等角的余角相等 B. 对顶角相等 C. 垂线段最短 D. 同位角相等 6. 等腰三角形的两条边长分别为 3和 7，则这个等腰三角形的周长是（ ） A. 10 B. 13 C. 17 D. 13 或 17 7. 若关于 x 的二次三项式 x2+ax+4是完全平方式，则 a的值是（ ） A. 4 B. 2 C. 4 D. 2 8. 如图，在ABC和ABD中，CABDAB，点 A，B，E 在同一
3、条直线上，则添加以下条件，仍然不能判定ABCABD的是（ ） A. BCBD B. CD C. CBEDBE D. ACAD 9. 如图，在ABC 中，AB的垂直平分线交 AB于点 D，交 BC于点 E，若 BC=6，AC=5，则ACE的周长为（ ） A. 8 B. 11 C. 16 D. 17 10. 已知点 P 为某个封闭图形边界上的一定点，动点 M从点 P 出发，沿其边界顺时针匀速运动一周，设点M 的运动时间为 x， 线段 PM 的长度为 y， 表示 y与 x的函数图象大致如图所示， 则该封闭图形可能是 （ ） A. B. C. D. 二、填空题（本大题二、填空题（本大题 4 个小题，每
4、小题个小题，每小题 4 分，共分，共 16 分）分） 11. 计算：63aa_ 12. 从1，0，2和 3中随机地选一个数，则选到正数的概率是 _ 13. 如图，ABCD，点 P在 CD 上，PF 平分EPC，155 ，则EPD_ 14. 如图，ABC 中，ACBC，点 D，E，F 分别在边 AC，AB，BC 上，且满足 ADBE，AEBF，DEF40 ，则C的度数是 _ 三三.解答题（本大题共解答题（本大题共 6 个小题，满分个小题，满分 54 分）分） 15. 计算： （1）2021( 2)2021()2 ； （2）（x+1） （x+2）+2（x1） x 16. （1）先化简，再求值： （
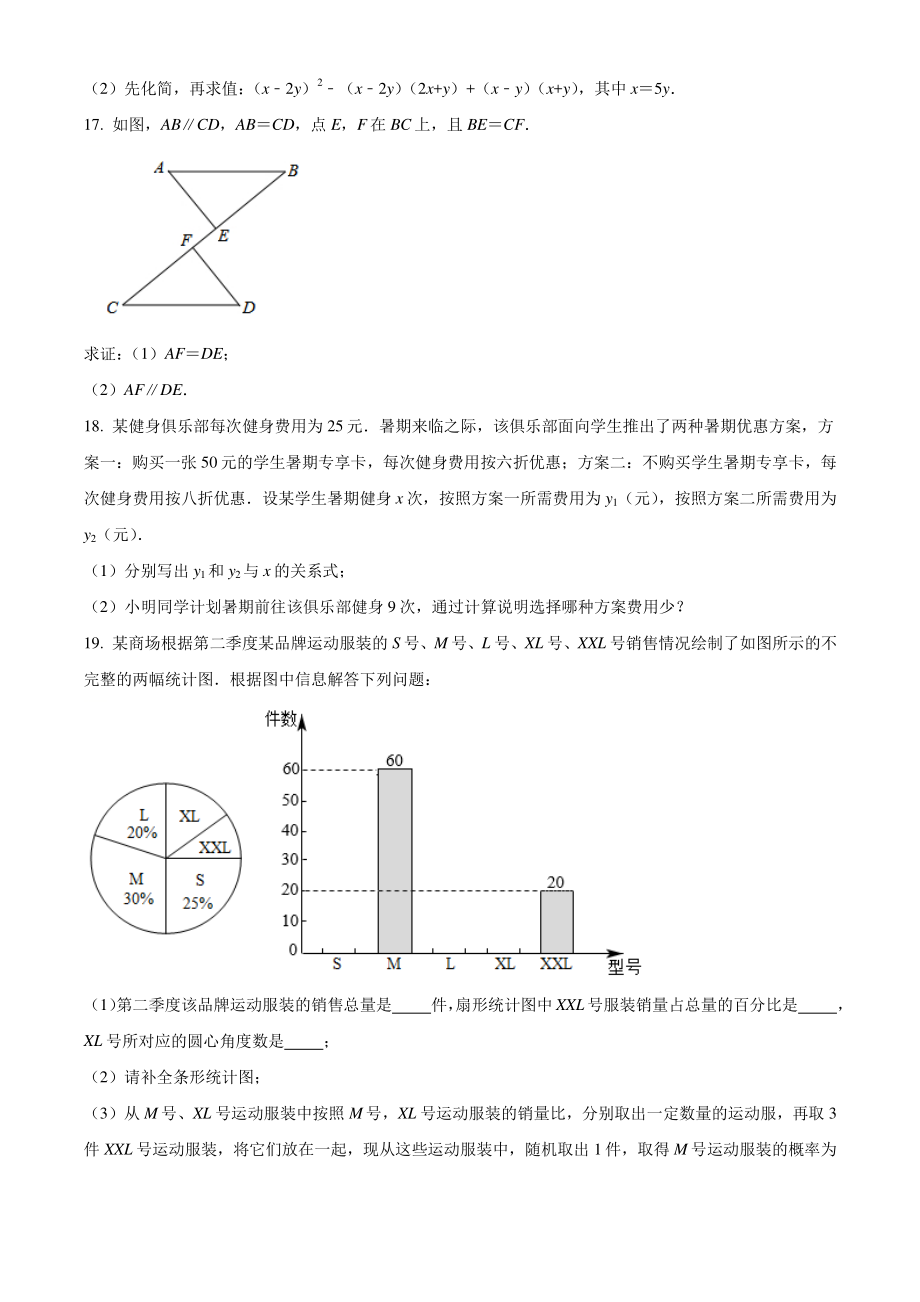
5、2x+3） （2x3）（x+2）2+4（x+3） ，其中 x2； （2）先化简，再求值： （x2y）2（x2y） （2x+y）+（xy） （x+y） ，其中 x5y 17. 如图，ABCD，ABCD，点 E，F 在 BC 上，且 BECF 求证： （1）AFDE； （2）AFDE 18. 某健身俱乐部每次健身费用为 25元暑期来临之际，该俱乐部面向学生推出了两种暑期优惠方案，方案一：购买一张 50元的学生暑期专享卡，每次健身费用按六折优惠；方案二：不购买学生暑期专享卡，每次健身费用按八折优惠设某学生暑期健身 x 次，按照方案一所需费用为 y1（元） ，按照方案二所需费用为y2（元） （1）分别
6、写出 y1和 y2与 x 的关系式； （2）小明同学计划暑期前往该俱乐部健身 9次，通过计算说明选择哪种方案费用少？ 19. 某商场根据第二季度某品牌运动服装的 S 号、M 号、L 号、XL号、XXL号销售情况绘制了如图所示的不完整的两幅统计图根据图中信息解答下列问题： （1） 第二季度该品牌运动服装的销售总量是 件， 扇形统计图中XXL号服装销量占总量的百分比是 ，XL号所对应的圆心角度数是 ； （2）请补全条形统计图； （3）从 M 号、XL 号运动服装中按照 M号，XL 号运动服装的销量比，分别取出一定数量的运动服，再取 3件 XXL号运动服装，将它们放在一起，现从这些运动服装中，随机取
7、出 1件，取得 M号运动服装的概率为35，求取出了 M号、XL号运动服装各多少件？ 20. 如图，点 P，Q分别是等边ABC 边 AB，BC上的动点（端点除外） ，点 P从点 A出发，沿 AB向点 B 方向运动， 同时， 点 Q 从点 B 出发， 以相同的速度沿 BC向点 C方向运动 连接 AQ， CP， AQ， CP 交于点 M （1）求证：AQCP； （2）求QMC的度数； （3）若点 P，Q分别运动到 AB，BC 的延长线上，直线 AQ，CP 交于点 M，请在备用图中补全图形，并求出QMC 的度数 一、填空题（每小题一、填空题（每小题 4 分，共分，共 20 分）分） 21. 若 a+b
8、3，a2+b27，则 ab_ 22. 从长度分别为 1cm，3cm，5cm，6cm的四条线段中随机取出三条，则能够成三角形的概率为 _ 23. 请按如图方法操作：对折长方形纸片 ABCD，使 AD 与 BC重合，得到折痕 EF；把纸片展平，在BC 上取点 M，沿 AM再次折叠纸片，并使点 B落在 EF 上的点 B处；把纸片展平，连接 AB则ABE的度数是 _ 24. 甲、乙两人在笔直的健身步道上同起点、同终点、同方向匀速步行 2400米，先到终点的人原地休息已知甲先出发 4分钟，在整个步行过程中，甲、乙两人的距离 y（米）与甲出发的时间 t（分）之间的关系如图所示，则甲、乙两人距离的最大值是
9、_米 25. 如图，AOB30 ，点 P 是AOB内的一定点，且 OP6，若点 M，N分别是射线 OA，OB上异于点O 的动点，则 PMN 周长的最小值是_ 二、解答题（本大题有二、解答题（本大题有 3 个小题，共个小题，共 30 分）分） 26. 若 a，b，c为ABC三边 （1）化简：|ab+c|+|cab|a+b|； （2）若 a，b，c 都是正整数，且 a2+b22a8b+170，ABC的周长 27. 在一条笔直的公 路上依次有 A，C，B 三地，甲、乙两人同时出发，甲从 A 地骑自行车去 B 地，途经 C地休息 1 分钟，继续按原速骑行至 B 地，甲到达 B 地后，立即按原路原速返回
10、 A 地；乙步行从 B 地前往 A地甲、乙两人距 A 地的路程 y（米）与时间 x（分）之间的函数关系如图所示，请结合图象解答下列问题： （1）请写出甲的骑行速度为 米/分，点 M 的坐标为 ； （2）求甲返回时距 A 地的路程 y 与时间 x 之间的函数关系式（不需要写出自变量的取值范围） ； （3）请直接写出两人出发后，在甲返回 A 地之前，经过多长时间两人距 C 地的路程相等 28. 如图，在边长为 8的正方形 ABCD中，点 E在边 AB上移动（不与端点重合） 连接 CE，以 CE为一边在其右侧作CEF，其中CEF90 ，CEEF，点 G为 FC的中点，过点 F作 FHAD，垂足为点
11、H，连接 GD，GH，FA （1）求证：EAF135 ； （2）请判断线段 GD 和 GH之间有何关系？写出你结论并证明； （3）在点 E 移动过程中，EAF 的面积有最大值吗？如果有，求出EAF 面积的最大值及此时 BE的长；如果没有，说明理由 2020-2021 学年四川省成都市成华区七年级学年四川省成都市成华区七年级下期末数学试卷下期末数学试卷 一、选择题（本大题共一、选择题（本大题共 10 个小题，每小题个小题，每小题 3 分，共分，共 30分）分） 1. 汽车以每小时 100 千米的速度匀速行驶，行驶的路程随时间的变化而变化，在这个变化过程中，自变量是（ ） A. 汽车 B. 路程
12、C. 速度 D. 时间 【1 题答案】 【答案】D 【解析】 【分析】根据自变量的定义解答即可 【详解】解：由题意得：在这一变化过程中，自变量是时间， 故选 D 【点睛】此题主要考查了自变量的定义，正确把握定义是解题关键 2. 下列四个图形中，不是轴对称图形的是（ ） A. B. C. D. 【2 题答案】 【答案】B 【解析】 【分析】根据轴对称图形在平面内沿一条直线折叠，直线两旁的部分能够完全重合的图形，对各选项进行一一分析即可 【详解】A、是轴对称图形故选项不合题意； B、不是轴对称图形故选项符合题意； C、是轴对称图形故选项不合题意； D、是轴对称图形故选项不合题意 故选：B 【点睛】
13、此题主要考查了轴对称图形概念，轴对称图形的关键是寻找对称轴，两边图象折叠后可重合 3. 肥皂泡的泡壁厚度大约是 0.00000071米，数字 0.00000071用科学记数法表示为（ ） A. 7.1 109 B. 7.1 108 C. 7.1 107 D. 7.1 106 【3 题答案】 【答案】C 【解析】 【分析】科学记数法的表示形式为 a10n的形式，其中 1|a|10，n为整数确定 n的值时，要看把原数变成 a 时， 小数点移动了多少位， n的绝对值与小数点移动的位数相同 当原数绝对值10 时， n 是正整数；当原数的绝对值1 时，n是负整数 【详解】解：0.000000717.1
14、107 故选：C 【点睛】此题考查科学记数法的表示方法科学记数法的表示形式为 a10n的形式，其中 1|a|10，n 为整数，表示时关键要确定 a 的值以及 n的值 4. 下列计算正确的是（ ） A. （a2）4a8 B. a2a4a8 C. （a+b）2a2+b2 D. a2+a2a4 【4 题答案】 【答案】A 【解析】 【分析】根据完全平方公式，幂的乘方公式，同底数幂的乘除法法则逐一判断选项即可 【详解】解：A. （a2）4a8，故该选项正确； B. a2a4a6，故该选项错误； C. （a+b）2a2+2ab+b2，故该选项错误； D. a2+a22a2，故该选项错误 故选 A 【点睛
15、】本题主要考查整式的运算，熟练掌握完全平方公式，幂的乘方公式，同底数幂的乘除法法则是解题的关键 5. 下列事件中，不是必然事件的是（ ） A. 等角的余角相等 B. 对顶角相等 C. 垂线段最短 D. 同位角相等 【5 题答案】 【答案】D 【解析】 【分析】根据必然事件的概念，逐一判断即可 【详解】解：A、等角的余角相等是必然事件，不符合题意； B、对顶角相等，是必然事件，不符合题意； C、垂线段最短，是必然事件，不符合题意； D、同位角相等，不是必然事件，符合题意 故选：D 【点睛】本题考查的是必然事件、不可能事件、随机事件的概念必然事件指在一定条件下，一定发生的事件不可能事件是指在一定条
16、件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件 6. 等腰三角形的两条边长分别为 3和 7，则这个等腰三角形的周长是（ ） A. 10 B. 13 C. 17 D. 13 或 17 【6 题答案】 【答案】C 【解析】 【分析】因为等腰三角形的两边为 3 和 7，但已知中没有点明底边和腰，所以有两种情况，需要分类讨论，还要注意利用三角形三边关系考虑各情况能否构成三角形 【详解】解：当 3为底时，其它两边都为 7，3、7、7可以构成三角形，周长为 17； 当 3为腰时，其它两边为 3 和 7， 3+3=67， 所以不能构成三角形，故舍去， 答案只有 17
17、 故选：C 【点睛】本题考查了等腰三角形的性质；对于底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论 7. 若关于 x 的二次三项式 x2+ax+4是完全平方式，则 a的值是（ ） A. 4 B. 2 C. 4 D. 2 【7 题答案】 【答案】C 【解析】 【分析】利用完全平方公式的结构特征判断即可求出 a的值 【详解】解：关于 x的二次三项式 x2+ax+4 是完全平方式， a4， 故选：C 【点睛】此题考查了完全平方式，熟练掌握完全平方公式是解本题的关键 8. 如图，在ABC和ABD中，CABDAB，点 A，B，E 在同一条直线上，则添加
18、以下条件，仍然不能判定ABCABD的是（ ） A. BCBD B. CD C. CBEDBE D. ACAD 【8 题答案】 【答案】A 【解析】 【分析】根据全等三角形的判定定理（SAS，ASA，AAS，SSS）判断即可 【详解】解：A、CABDAB，ABAB，BCBD， 根据 SSA不能推出ABCABD，故本选项符合题意； B、CABDAB，CD，ABAB， 根据 AAS能推出ABCABD，故本选项不符合题意； C、CBEDBE， ABCABD， CABDAB，ABAB，ABCABD， 根据 ASA能推出ABCABD，故本选项不符合题意； D、ABAB，CABDAB，ACAD 根据 SAS
19、能推出ABCABD，故本选项不符合题意 故选：A 【点睛】本题考查了全等三角形判定定理的应用，注意：全等三角形的判定定理有：SAS，ASA，AAS，SSS 9. 如图，在ABC 中，AB的垂直平分线交 AB于点 D，交 BC于点 E，若 BC=6，AC=5，则ACE的周长为（ ） A. 8 B. 11 C. 16 D. 17 【9 题答案】 【答案】B 【解析】 【分析】根据线段垂直平分线的性质得 AE=BE，然后利用等量代换即可得到ACE 的周长=AC+BC，再把BC=6，AC=5代入计算即可 【详解】解：DE垂直平分 AB， AE=BE， ACE的周长=AC+CE+AE =AC+CE+BE
20、 =AC+BC =5+6 =11 故选 B 【点睛】 本题考查了线段垂直平分线的性质：垂直平分线垂直且平分其所在线段；垂直平分线上任意一点，到线段两端点的距离相等 10. 已知点 P 为某个封闭图形边界上的一定点，动点 M从点 P 出发，沿其边界顺时针匀速运动一周，设点M 的运动时间为 x， 线段 PM 的长度为 y， 表示 y与 x的函数图象大致如图所示， 则该封闭图形可能是 （ ） A. B. C. D. 【10 题答案】 【答案】A 【解析】 【详解】分析：先观察图象得到 y与 x 的函数图象分三个部分，则可对有 4边的封闭图形进行淘汰，利用圆的定义，P 点在圆上运动时，PM 总上等于半
21、径，则可对 D 进行判断，从而得到正确选项 详解： y与 x的函数图象分三个部分， 而 B 选项和 C选项中的封闭图形都有 4条线段， 其图象要分四个部分，所以 B、C选项不正确；D选项中的封闭图形为圆，y为定中，所以 D选项不正确；A 选项为三角形，M点在三边上运动对应三段图象，且 M点在 P 点的对边上运动时，PM的长有最小值 故选 A 点睛：本题考查了动点问题的函数图象：函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力用图象解决问题时，要理清图象的含义即会识图 二、填空题（本大题二、填空题（本大题 4 个小题，
22、每小题个小题，每小题 4 分，共分，共 16 分）分） 11. 计算：63aa_ 【11 题答案】 【答案】3a 【解析】 【分析】利用同底数幂相除的法则计算即可 【详解】解：63633aaaaa， 故答案为：3a 【点睛】本题考查整式的乘除，掌握积的乘方与同底数幂相除的法则是解题的关键 12. 从1，0，2和 3中随机地选一个数，则选到正数的概率是 _ 【12 题答案】 【答案】12#0.5 【解析】 【分析】根据概率公式直接求解即可 【详解】解：1，0，2 和 3中有 2 个正数， 选到正数的概率=2142， 故答案是：12 【点睛】本题主要考查等可能事件的概率，熟练掌握概率公式是解题的关
23、键 13. 如图，ABCD，点 P在 CD 上，PF 平分EPC，155 ，则EPD_ 【13 题答案】 【答案】70 【解析】 【分析】根据平行线和角平分线的定义即可得到结论 详解】解：ABCD， 1CPF55， PF 是EPC的平分线， CPE2CPF110， EPD18011070 ， 故答案是：70 【点睛】本题考查了平行线的性质以及角平分线的定义，熟练掌握平行线的性质是解题的关键 14. 如图，ABC 中，ACBC，点 D，E，F 分别在边 AC，AB，BC 上，且满足 ADBE，AEBF，DEF40 ，则C的度数是 _ 【14 题答案】 【答案】100 【解析】 【分析】先证明AD
24、EBEF，可得AED=BFE，从而得BFE+BEF=140，进而即可求解 【详解】解：ABC中，ACBC， A=B， ADBE，AEBF， ADEBEF， AED=BFE， DEF40 ， AED+BEF=180-40=140， BFE+BEF=140， B=A=40， C=180-40-40=100 故答案是：100 【点睛】本题主要考查全等三角形的判定和性质以及三角形内角和定理以及等腰三角形的性质，证明ADEBEF是解题的关键 三三.解答题（本大题共解答题（本大题共 6 个小题，满分个小题，满分 54 分）分） 15. 计算： （1）2021( 2)2021()2 ； （2）（x+1） （
25、x+2）+2（x1） x 【15 题答案】 【答案】 （1）7； （2）x+5 【解析】 【分析】 （1）先算乘方，零指数幂和负整数指数幂，再算加减法，即可求解； （2）先算多项式乘多项式和单项式乘多项式，再算除法，即可求解 【详解】解： （1）原式=4 14 =7； （2）原式= （x2+3x+2+2x2） x =（x2+5x） x = x+5 【点睛】本题主要考查实数的混合运算和整式的混合运算，熟练掌握零指数幂和负整数指数幂以及整式的混合运算法则，是解题的关键 16. （1）先化简，再求值： （2x+3） （2x3）（x+2）2+4（x+3） ，其中 x2； （2）先化简，再求值： （x2
26、y）2（x2y） （2x+y）+（xy） （x+y） ，其中 x5y 【16 题答案】 【答案】 （1）3x2-1，11； （2）xy+5y2，0 【解析】 【分析】 （1）先利用完全平方公式和平方差公式计算，再合并同类项，最后代入求值即可； （2） 先利用完全平方公式和平方差公式以及多项式乘多项式法则计算， 再合并同类项， 最后代入求值即可 【详解】解： （1）原式=4x2-9(x2+4x+4)+4x+12 =4x2-9x2-4x-4+4x+12 =3x2-1， 当 x2时，原式=3（-2）2-1=11； （2）原式=（x24xy+4y2）（2x23xy-2y2）+x2y2 = x24xy+
27、4y2-2x2+3xy+2y2+x2y2 =xy+5y2， 当 x5y时，原式=xy+5y2=-5y2+5y2=0 【点睛】本题主要考查整式的化简求值，熟练掌握乘法公式和整式的运算法则，是解题的关键 17. 如图，ABCD，ABCD，点 E，F 在 BC 上，且 BECF 求证： （1）AFDE； （2）AFDE 【17 题答案】 【答案】 （1）见详解； （2）见详解 【解析】 【分析】 （1）由等式的性质就可以得出 BFCE，由平行线的性质就可以得出BC，根据 SAS 证明ABFDCE，进而可以得出结论； （2）由ABFDCE就可以得出AFBDEC，进而可以得出结论 【详解】证明：BECF
28、， BE-EFCF-EF， BFCE ABCD， BC ABF 和DCE 中 ABCDBCBFCE ， ABFDCE（SAS） ， AFDE； （2）ABFDCE， AFBDEC， AFEDEF， AFDE 【点睛】本题考查了平行线的性质，全等三角形的判定及性质，解答时证明三角形全等是关键 18. 某健身俱乐部每次健身费用为 25元暑期来临之际，该俱乐部面向学生推出了两种暑期优惠方案，方案一：购买一张 50元的学生暑期专享卡，每次健身费用按六折优惠；方案二：不购买学生暑期专享卡，每次健身费用按八折优惠设某学生暑期健身 x 次，按照方案一所需费用为 y1（元） ，按照方案二所需费用为y2（元）
29、（1）分别写出 y1和 y2与 x 的关系式； （2）小明同学计划暑期前往该俱乐部健身 9次，通过计算说明选择哪种方案费用少？ 【18 题答案】 【答案】 （1）y115x50，y220 x； （2）选择方案二所需费用更少 【解析】 【分析】 （1）根据两种健身方案的数量关系，直接列出函数解析式即可； （2）将 x9分别代入 y1、y2关于 x的函数解析式，比较即可 【详解】解： （1）由题意得：y10.625x50，即：y115x50， y20.825x，即：y220 x； （2）当健身 9 次时， 选择方案一所需费用：y115950185（元） ， 选择方案二所需费用：y2209180（元
30、） ， 180185， 选择方案二所需费用更少 【点睛】本题考查了一次函数的应用，解题的关键是理解两种优惠活动方案，求出 y1、y2关于 x 的函数解析式 19. 某商场根据第二季度某品牌运动服装的 S 号、M 号、L 号、XL号、XXL号销售情况绘制了如图所示的不完整的两幅统计图根据图中信息解答下列问题： （1） 第二季度该品牌运动服装的销售总量是 件， 扇形统计图中XXL号服装销量占总量的百分比是 ，XL号所对应的圆心角度数是 ； （2）请补全条形统计图； （3）从 M 号、XL 号运动服装中按照 M号，XL 号运动服装的销量比，分别取出一定数量的运动服，再取 3件 XXL号运动服装，将它
31、们放在一起，现从这些运动服装中，随机取出 1件，取得 M号运动服装的概率为35，求取出了 M号、XL号运动服装各多少件？ 【19 题答案】 【答案】 （1）200，10%，54； （2）见详解； （3）取出了 M号、XL号运动服装各 18件和 9 件 【解析】 【分析】 （1）由 M号的销售量及其所占的百分比求出运动服装总销量，再求出 XXL号运动服装销量的百分比，根据各组所占百分比的和为单位 1求出 XL 号运动服装销量的百分比，从而求出圆心角度数； （2）用运动服装总销量分别乘以 S号，L 号，XL号所占的百分比，得到对应服装销量，即可补全条形统计图； （3）根据题意列出分式方程，求解即可
32、 【详解】解： （1）6030%200（件） ， 20200100%10%， 125%30%20%10%15%，36015%=54， 故答案是：200，10%，54； （2）S号服装销量：20025%50（件） ， L号服装销量：20020%40（件） ， XL号服装销量：20015%30（件） ， 条形统计图补充如下： （3）设取出了 M 号、XL号运动服装各 2x 件，x件， 由题意得：23235xxx，解得：x=9， 经检验：x=9是方程的解， 2x=18， 答：取出了 M号、XL号运动服装各 18件和 9 件 【点睛】本题考查了条形统计图、扇形统计图和利用统计图获取信息的能力；利用统计
33、图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题也考查了概率公式 20. 如图，点 P，Q分别是等边ABC 边 AB，BC上的动点（端点除外） ，点 P从点 A出发，沿 AB向点 B 方向运动， 同时， 点 Q 从点 B 出发， 以相同的速度沿 BC向点 C方向运动 连接 AQ， CP， AQ， CP 交于点 M （1）求证：AQCP； （2）求QMC的度数； （3）若点 P，Q分别运动到 AB，BC 的延长线上，直线 AQ，CP 交于点 M，请在备用图中补全图形，并求出QMC 的度数 【20 题答案】 【答案】 （1）见详解； （2）60； （3）120 【解析】
34、【分析】 （1）根据等边三角形的性质，利用 SAS 证明ABQCAP即可； （2）先判定ABQCAP，根据全等三角形的性质可得BAQACP，从而得到QMC60； （3） 先补全图形， 由 （1） 可知ABQCAP， 根据全等三角形的性质可得BAQACP， 从而得到QMC120 【详解】解： （1）证明：ABC是等边三角形 ABQCAP60，ABCA， 又点 P、Q 运动速度相同， APBQ， 在ABQ与CAP中， ABCAABQCAPAPBQ ， ABQCAP（SAS） ， AQCP； （2）ABQCAP， BAQACP， QMC 是ACM 的外角， QMCACPMACBAQMACBAC BA
35、C60， QMC60； （3）补全图形如下： 由（1）可得，ABQCAP， BAQACP， QMC 是APM 的外角， QMCBAQAPM， QMCACPAPM180PAC18060120 【点睛】此题是三角形综合题，主要考查了等边三角形的性质、全等三角形的判定与性质，三角形外角的性质等知识的综合应用解决问题的关键是掌握全等三角形的判定方法：两边及其夹角分别对应相等的两个三角形全等解题时注意运用全等三角形的对应边相等，对应角相等的性质 一、填空题（每小题一、填空题（每小题 4 分，共分，共 20 分）分） 21. 若 a+b3，a2+b27，则 ab_ 【21 题答案】 【答案】1 【解析】
36、【分析】根据完全平方公式，可得答案 【详解】 （a+b）2329， （a+b）2a2+b2+2ab9 a2+b27， 2ab2， ab1， 故答案为 1 【点睛】本题考查了完全平方公式，利用完全平方公式是解题关键 22. 从长度分别为 1cm，3cm，5cm，6cm四条线段中随机取出三条，则能够成三角形的概率为 _ 【22 题答案】 【答案】14 【解析】 【分析】列举出所有可能出现的结果情况，进而求出能构成三角形的概率 【详解】解：从长度为 1cm、3cm、5cm、6cm四条线段中随机取出三条， 共有以下 4 种结果（不分先后） ： 1cm、3cm、5cm， 1cm、3cm、6cm， 3cm
37、、5cm、6cm， 1cm、5cm、6cm， 其中，能构成三角形的只有 1种， P（构成三角形）14 故答案是：14 【点睛】本题考查随机事件发生的概率，列举出所有可能出现的结果情况，是正确解答的关键 23. 请按如图方法操作：对折长方形纸片 ABCD，使 AD 与 BC重合，得到折痕 EF；把纸片展平，在BC 上取点 M，沿 AM再次折叠纸片，并使点 B落在 EF 上的点 B处；把纸片展平，连接 AB则ABE的度数是 _ 【23 题答案】 【答案】30 【解析】 【分析】根据折叠的性质得 A B=AB=2AE，再根据直角三角形的性质，即可求解 【详解】解：对折长方形纸片 ABCD，使 AD与
38、 BC重合， AEF=90，2AE=AB， 沿 AM再次折叠纸片，并使点 B 落在 EF上的点 B处， A B=AB=2AE， ABE=30 故答案是：30 【点睛】 本题主要考查折叠的性质和矩形的性质， 熟练掌握含 30角的直角三角形的性质， 是解题的关键 24. 甲、乙两人在笔直的健身步道上同起点、同终点、同方向匀速步行 2400米，先到终点的人原地休息已知甲先出发 4分钟，在整个步行过程中，甲、乙两人的距离 y（米）与甲出发的时间 t（分）之间的关系如图所示，则甲、乙两人距离的最大值是 _米 【24 题答案】 【答案】360 【解析】 【分析】根据题意和函数图象中的数据分别求出甲、乙的速
39、度，再求出乙到达终点时，甲离终点距离从而可以解答本题 【详解】解：由题意可得：甲步行速度240460（米/分） ， 设乙的速度为：x米/分， 由题意可得：16 60（164）x， 解得 x80 乙的速度为 80米/分， 乙走完全程的时间24008030（分） ， 乙到达终点时，甲离终点距离是：2400（430）60360（米） ， 甲、乙两人距离的最大值是 360米 故答案是 360 【点睛】本题考查一次函数的应用，解答本题的关键是明确题意，理解函数图像上点的坐标的实际意义，利用数形结合的思想解答 25. 如图，AOB30 ，点 P 是AOB内的一定点，且 OP6，若点 M，N分别是射线 OA
40、，OB上异于点O 的动点，则 PMN 周长的最小值是_ 【25 题答案】 【答案】6 【解析】 【分析】设点 P 关于 OA的对称点为 C，关于 OB的对称点为 D，当点 M、N在 CD上时，PMN 的周长最小，利用等边三角形的判定和性质即可得出结果 【详解】解：分别作点 P关于 OA、OB的对称点 C、D，连接 CD，分别交 OA、OB于点 M、N，连接 OP、OC、OD、PM、PN 点 P关于 OA 的对称点为 C，关于 OB 的对称点为 D， PM=CM，OP=OC，COA=POA； 点 P关于 OB 的对称点为 D， PN=DN，OP=OD，DOB=POB， OC=OD=OP=6cm，
41、COD=COA+POA+POB+DOB=2POA+2POB=2AOB=60 ， COD是等边三角形， CD=OC=OD=6 PMN 的周长的最小值=PM+MN+PN=CM+MN+DNCD=6 故答案为 6 【点睛】此题主要考查轴对称-最短路线问题，熟知两点之间线段最短是解答此题的关键 二、解答题（本大题有二、解答题（本大题有 3 个小题，共个小题，共 30 分）分） 26. 若 a，b，c为ABC的三边 （1）化简：|ab+c|+|cab|a+b|； （2）若 a，b，c 都是正整数，且 a2+b22a8b+170，ABC的周长 【26 题答案】 【答案】 （1）ab； （2）9 【解析】 【
42、分析】 （1）根据三角形的三边关系化简即可； （2）根据非负数的性质和三角形的三边关系化简即可得到结论 【详解】解： （1）a，b，c为ABC三边， ab+c0，cab0，a+b0， |ab+c|+|cab|a+b|ab+cc+a+babab； （2）a2+b22a8b+17（a22a+1）+（b28b+16）（a1）2+（b4）20， a1，b4， a，b，c 为ABC的三边， 41c4+1， 3c5， 若 a，b，c都是正整数， c4， ABC的周长1+4+49 【点睛】本题考查了配方法的应用，非负数的性质，三角形的三边关系，正确的理解题意是解题的关键 27. 在一条笔直的公 路上依次有
43、A，C，B 三地，甲、乙两人同时出发，甲从 A 地骑自行车去 B 地，途经 C地休息 1 分钟，继续按原速骑行至 B 地，甲到达 B 地后，立即按原路原速返回 A 地；乙步行从 B 地前往 A地甲、乙两人距 A 地的路程 y（米）与时间 x（分）之间的函数关系如图所示，请结合图象解答下列问题： （1）请写出甲的骑行速度为 米/分，点 M 的坐标为 ； （2）求甲返回时距 A 地的路程 y 与时间 x 之间的函数关系式（不需要写出自变量的取值范围） ； （3）请直接写出两人出发后，在甲返回 A 地之前，经过多长时间两人距 C 地的路程相等 【27 题答案】 【答案】 （1）240， （6，120
44、0） ； （2）y=240 x+2640； （3）经过 4 分钟或 6 分钟或 8 分钟时两人距 C 地的路程相等 【解析】 【分析】(1)根据函数图象得出 AB两地的距离,由行程问题的数量关系由路程时间=速度就可以求出结论; (2)先由行程问题的数量关系求出 M、N的坐标,设 y与 x之间的函数关系式为 y=kx+b,由待定系数法就可以求出结论; (3) 设甲返回 A 地之前，经过 x 分两人距 C 地的路程相等，可得乙的速度：120020=60（米/分） ，分别分当 0 x3 时当 3x1 时当x6 时当 x=6 时当 x6 时 5 种情况讨论可得经过多长时间两人距 C 地的路程相等. 【
45、详解】 （1）由题意得：甲的骑行速度为： =240（米/分） ， 240（111）2=1200（米） ， 则点 M 的坐标为（6，1200） ， 故答案为 240， （6，1200） ； （2）设 MN 的解析式为：y=kx+b（k0） ， y=kx+b（k0）的图象过点 M（6，1200） 、N（11，0） ， ， 解得， 直线 MN 的解析式为：y=240 x+2640； 即甲返回时距 A 地的路程 y 与时间 x 之间的函数关系式：y=240 x+2640； （3）设甲返回 A 地之前，经过 x 分两人距 C 地的路程相等， 乙的速度：120020=60（米/分） ， 如图 1 所示：A
46、B=1200，AC=1020， BC=12001020=180， 分 5 种情况： 当 0 x3 时，1020240 x=18060 x， x=3， 此种情况不符合题 意； 当 3x1 时，即 3x，甲、乙都在 A、C 之间， 1020240 x=60 x180， x=4， 当x6 时，甲在 B、C 之间，乙在 A、C 之间， 240 x1020=60 x180， x=， 此种情况不符合题意； 当 x=6 时，甲到 B 地，距离 C 地 180 米， 乙距 C 地的距离：660180=180（米） ， 即 x=6 时两人距 C 地的路程相等， 当 x6 时，甲在返回途中， 当甲在 B、C 之间
47、时，180240（x1）1200=60 x180，x=6， 此种情况不符合题意， 当甲在 A、C 之间时，240（x1）1200180=60 x180， x=8， 综上所述，在甲返回 A 地之前，经过 4 分钟或 6 分钟或 8 分钟时两人距 C 地的路程相等 【点睛】 本题考查了待定系数法一次函数的解析式的运用,一次函数与二元一次方程组的关系的运用,行程问题的数量关系的运用,注意由图像得出有用的信息及分类讨论思想在解题时的应用. 28. 如图，在边长为 8的正方形 ABCD中，点 E在边 AB上移动（不与端点重合） 连接 CE，以 CE为一边在其右侧作CEF，其中CEF90 ，CEEF，点
48、G为 FC的中点，过点 F作 FHAD，垂足为点 H，连接 GD，GH，FA （1）求证：EAF135 ； （2）请判断线段 GD 和 GH之间有何关系？写出你的结论并证明； （3）在点 E 移动过程中，EAF 的面积有最大值吗？如果有，求出EAF 面积的最大值及此时 BE的长；如果没有，说明理由 【28 题答案】 【答案】 （1）见详解； （2）DGGH，DG=GH，理由见详解； （3） EAF 面积的最大值=8，此时，BE=4 【解析】 【分析】 （1）过点 F 作 FNBA 于点 N，证明CBEENF，可得 EN=BC=AB，BE=FN，进而即可得到结论； （2）延长 HG交 CD 于点
49、 M，可证FGHCGM，从而得DMH是等腰直角三角形，进而即可得到结论； （3）设 EA=x，则 BE=FN=8-x，根据三角形面积公式，得到21482EAFSx，进而即可求解 【详解】 （1）证明：过点 F作 FNBA 于点 N， FNE=90，即：EFN+FEN=90， CEF90 ， CEB+FEN=90， EFN=CEB， 在CBE和ENF中， 90BENFEFNCEBCEEF， CBEENF EN=BC=AB，BE=FN， AB-AE=EN-AE，即：BE=AN=FN， AFN是等腰直角三角形，即：FAN=45， EAF180-FAN =135 ； （2）DGGH，DG=GH，理由如
50、下： 延长 HG交 CD于点 M， FHAD， FHD=CDA=90， CDFH， GCM=GFH，GMC=GHF， G 为 CF 的中点， FG=CG， FGHCGM， CM=FH，GM=GH， FHA=HAN=ANF=90，AN=FN， 四边形 ANFH是正方形， AH=FH=CM， AD-AH=CD-CM，即：DH=DM， DMH是等腰直角三角形， MG=HG， DGGH，DG=GH； （3）设 EA=x，则 BE=8-x， 由（1）可知：BE=FN， FN=8-x， FNEA， 2111848222EAFSEA FNxxx， 当 x=4 时， EAF面积的最大值=8， 此时，BE=8-
