1、2022年山东省潍坊市诸城市中考三模数学试题一、选择题（每小题选对得3分，多选、不选、错选均记0分）1. 如图，数轴上有A，B，C，D四点，以下线段中，长度最接近的是（）A. 线段ABB. 线段ACC. 线段CDD. 线段BC2. 下列计算正确的是（ ）A. B. C D. 3. 下列因式分解正确的是（ ）A. B. C. D. 4. 不等式组的解集在数轴上表示为（）A. B. C. D. 5. 如图，点A到点C的距离为100米，要测量河对岸B点到河岸AD的距离小明在A点测得B在北偏东60的方向上，在C点测得B在北偏东30的方向上，则B点到河岸AD的距离为（）A. 100米B. 50米C. 米
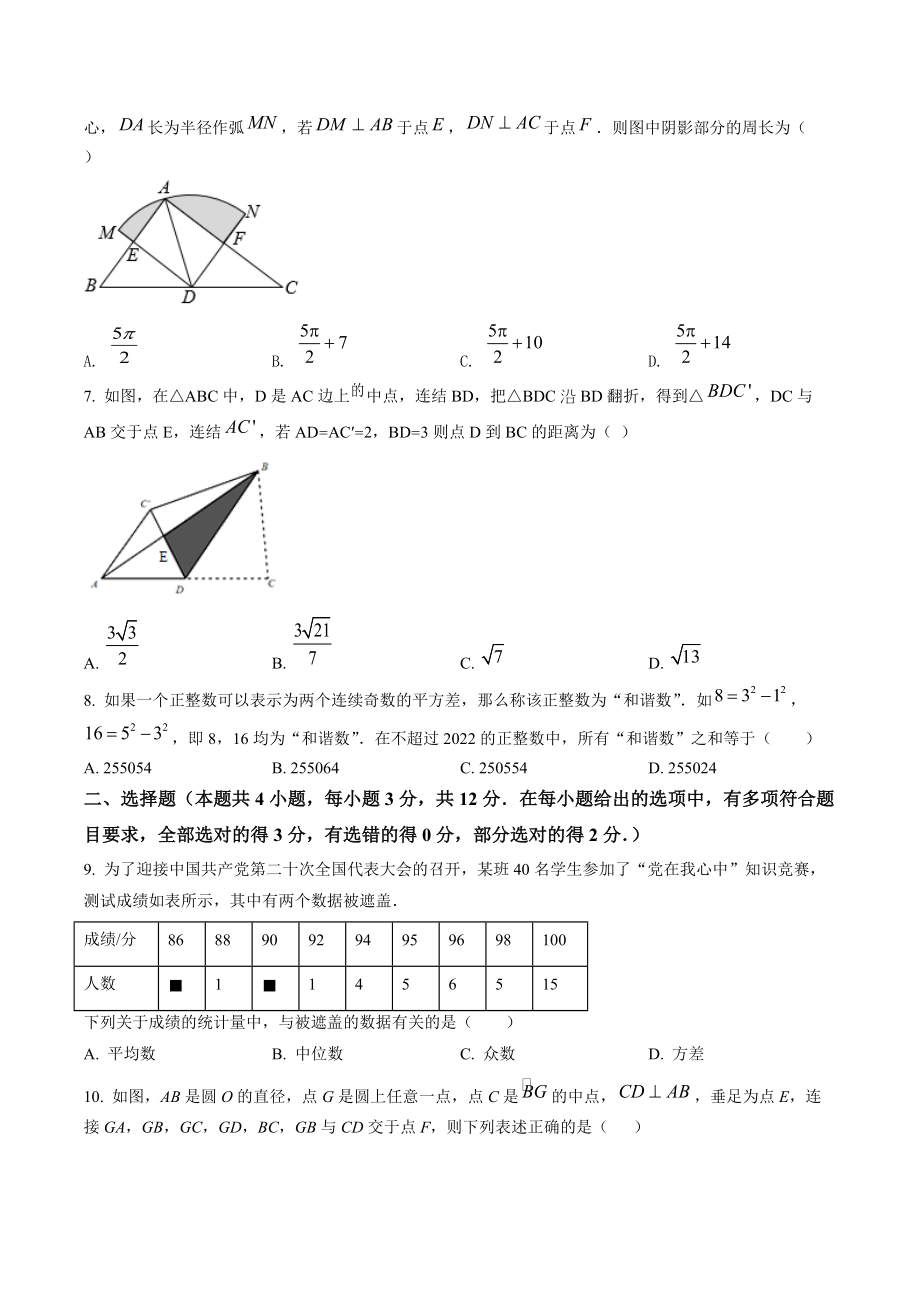
2、D. 50米6. 如图，在中，为的中点，连接，以点为圆心，长为半径作弧，若于点，于点则图中阴影部分的周长为（ ）A. B. C. D. 7. 如图，在ABC中，D是AC边上中点，连结BD，把BDC沿BD翻折，得到，DC与AB交于点E，连结，若AD=AC=2，BD=3则点D到BC的距离为（ ）A. B. C. D. 8. 如果一个正整数可以表示为两个连续奇数的平方差，那么称该正整数为“和谐数”如，即8，16均为“和谐数”在不超过2022的正整数中，所有“和谐数”之和等于（ ）A. 255054B. 255064C. 250554D. 255024二、选择题（本题共4小题，每小题3分，共12分在每
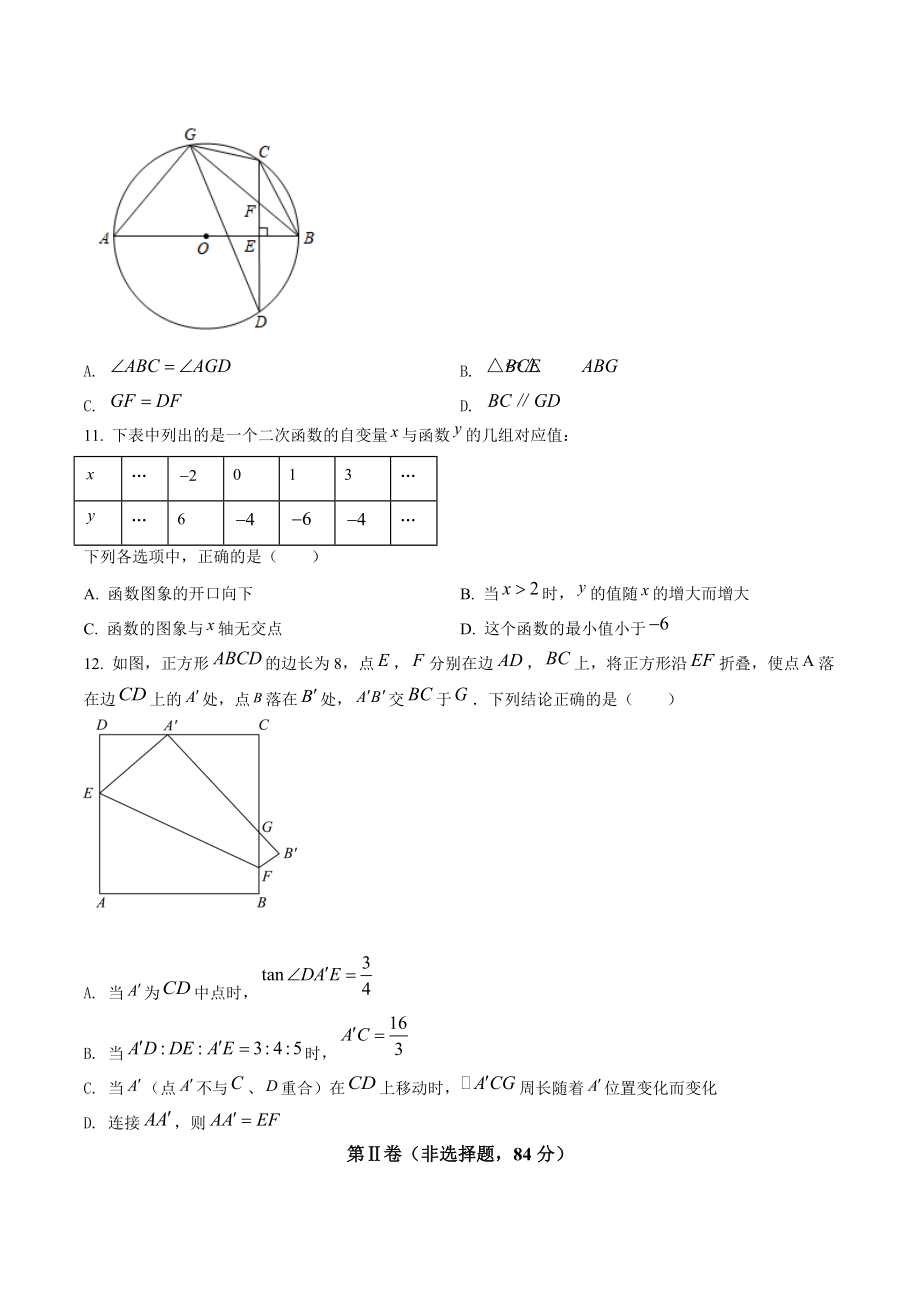
3、小题给出的选项中，有多项符合题目要求，全部选对的得3分，有选错的得0分，部分选对的得2分）9. 为了迎接中国共产党第二十次全国代表大会的召开，某班40名学生参加了“党在我心中”知识竞赛，测试成绩如表所示，其中有两个数据被遮盖成绩/分8688909294959698100人数11456515下列关于成绩的统计量中，与被遮盖的数据有关的是（ ）A. 平均数B. 中位数C. 众数D. 方差10. 如图，AB是圆O的直径，点G是圆上任意一点，点C是的中点，垂足为点E，连接GA，GB，GC，GD，BC，GB与CD交于点F，则下列表述正确的是（ ）A. B. C. D. 11. 下表中列出的是一个二次函数
4、的自变量与函数的几组对应值：0136下列各选项中，正确的是（ ）A. 函数图象的开口向下B. 当时，的值随的增大而增大C. 函数的图象与轴无交点D. 这个函数的最小值小于12. 如图，正方形的边长为8，点，分别在边，上，将正方形沿折叠，使点落在边上的处，点落在处，交于下列结论正确的是（ ）A. 当为中点时，B. 当时，C. 当（点不与、重合）在上移动时，周长随着位置变化而变化D. 连接，则第卷（非选择题，84分）三、填空题（本题共4小题，共12分，只要求填写最后结果，每小题填对得3分）13. 若一次函数的图象经过第一、二、四象限，则化简_14. 若，是一元二次方程两个实数根，则的值是_15.
5、如图，函数和的图像分别是和设点在上，轴交于点，轴交于点，的面积_16. 如图，已知的内角，分别作内角与外角的平分线，两条平分线交于，得；和的平分线交于，得；，以此类推得到，则_（用表示）四、解答题（本题共7小题，共72分解答应写出必要文字说明或演算步骤）17. 某校为了“中考体测”的顺利进行，引导同学们积极参加体育锻炼，学校购买了一批跳绳供学生借用，现从九年级随机抽取了部分学生对新跳绳进行测试，绘制了如下的两幅不完整的统计表和统计图请根据相关信息，解答下列问题：一分钟跳绳成绩的分组统计表 组别跳绳次数分段频数A10BC42D13一分钟跳绳成绩的扇形统计图（1）本次接受随机抽样调查的学生人数为
6、人，统计表中的的值为 ；（2）抽取学生一分钟跳绳成绩的中位数所在的组别是 ；（3）现在指定两名男生和两名女生负责跳绳发放和整理工作，若两人一组，随机组合，则恰好分组都是一男一女的概率是多少？18. 自“新冠”病毒出现后，瓶装酒精成了人们家中常备之物一种酒精消毒瓶如图1，AB为喷嘴，BCD为按压柄，CE为伸缩连杆，BE和EF为导管，其示意图如图2，DBEBEF108，BD6cm，BE4cm当按压柄BCD按压到底时，BD转动到，此时EF（如图3）（1）求BD转动到扫过的面积（结果保留）；（2）求点D到直线EF的距离（结果精确到0.1cm）（参考数据：sin360.59，cos360.81，tan3
7、60.73，sin720.95，cos720.31，tan723.08）19. 数学是一个不断思考，不断发现，不断归纳过程，古希腊数学家帕普斯（Pappus，约300350）把三等分的操作如下：以点为坐标原点，所在的直线为轴建立平面直角坐标系；在平面直角坐标系中，绘制反比例函数的图象，图象与的边交于点；以点为圆心，为半径作弧，交函数的图象于点；分别过点和作轴和轴的平行线，两线交于点，；作射线，交于点，得到（1）任务一：判断四边形的形状，并证明；（2）任务二：请证明20. 点M，N为正方形ABCD平面内两点，BMBN（1）如图1，点M为边CD上一点，D，A，N三点共线求证：BMBN（2）如图2，
8、点M为正方形ABCD外一点，CMMN，M，A，N三点共线BMBN是否仍然成立，请说明理由（3）在（2）条件下，若CM1，BN4，求正方形的边长21. 如图，是某同学正在设计的一动画示意图，轴上依次有，三个点，且，在上方有五个台阶（各拐角均为），每个台阶的高、宽分别是1和1.5，台阶到轴距离从点处向右上方沿抛物线发出一个带光的点（1）求点的横坐标，且在图中补画出轴，并直接指出点会落在哪个台阶上；（2）当点落到台阶上后立即弹起，又形成了另一条与形状相同的抛物线，且最大高度为11，求抛物线的表达式22. 如图，上有，三点，是直径，点是的中点，连接交于，在延长线上，且（1）求证：是的切线；（2）若，求
9、的半径和的值23. 综合与探究如图，抛物线与轴交于，两点，与轴交于点，点，的坐标分别为(2，0)，(0，3)，点与点关于轴对称，是直线上方抛物线上一动点，连接、交于点（1）求抛物线的函数表达式及点的坐标；（2）在点运动的过程中，求：的最大值；（3）在轴上是不存在点，使？若存在，请直接写出点的坐标；若不存在，请说明理由2022年山东省潍坊市诸城市中考三模数学试题一、选择题（每小题选对得3分，多选、不选、错选均记0分）1. 如图，数轴上有A，B，C，D四点，以下线段中，长度最接近的是（）A. 线段ABB. 线段ACC. 线段CDD. 线段BC【答案】A【解析】【分析】23，依次估计线段AB、AC、
10、CD、BC的长度范围，和进行比较即可【详解】选项A、线段AB长度范围大于2且小于3；选项B、线段AC长度范围是大于4而小于5；选项C、线段CD长度是4；选项D、线段BC长度是2；23，最接近的是线段AB长度，所以答案选A【点睛】本题考查了无理数大小的估计，会进行无理数大小的估计是本题的解题关键2. 下列计算正确的是（ ）A. B. C. D. 【答案】B【解析】【分析】根据算术平方根的性质、同底数幂除法、合并同类项法则及幂的乘方法则逐一计算即可得答案【详解】A、，故该选项计算错误，不符合题意；B、，故该选项计算正确，符合题意；C、+=，故该选项计算错误，不符合题意；D、，故该选项计算错误，不符
11、合题意；故选：D【点睛】本题考查算术平方根的性质、同底数幂除法、合并同类项法则及幂的乘方法则，熟练掌握运算法则是解题关键3. 下列因式分解正确的是（ ）A. B. C. D. 【答案】D【解析】【分析】根据因式分解的定义化简判断【详解】解：A. ，故此选项不合题意；B.，无法运用平方差公式分解因式，故此选项不合题意；C. ，故此选项不合题意；D，故此选项符合题意故选：D【点睛】本题考查因式分解：把一个多项式化成几个整式积的形式，像这样的式子变形叫做这个多项式的因式分解，也叫做把这个多项式分解因式；因式分解的结果是整式的乘积的形式且结果必须分解到不能再分解为止，这是判断是否是因式分解的根据方法，
12、掌握因式分解的方法是解题的关键4. 不等式组的解集在数轴上表示为（）A. B. C. D. 【答案】A【解析】【分析】分别求出每一个不等式解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集【详解】解：解不等式x23，得：x2，解不等式82x4，得：x2，则不等式组的解集为2x2，故选：A【点睛】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键5. 如图，点A到点C的距离为100米，要测量河对岸B点到河岸AD的距离小明在A点测得B在北偏东60的方向上，在C点测得B在北
13、偏东30的方向上，则B点到河岸AD的距离为（）A. 100米B. 50米C. 米D. 50米【答案】D【解析】【分析】过B作BMAD于M，先证BADABC，得BCAC100米，再在RtBCM中，由锐角三角函数定义求出BM即可【详解】解：过B作BMAD于M，如图：由题意得：BAD906030，BCD903060，ABCBCDBAD30，BADABC，BCAC100米，BMAD，BMC90，在RtBCM中，sinBCM， BMBCsinBCM10050， 即B点到河岸AD的距离为50米，故选：D【点睛】此题主要考查了解直角三角形的应用以及等腰三角形的判定等知识，正确作出辅助线构造直角三角形是解题的
14、关键6. 如图，在中，为的中点，连接，以点为圆心，长为半径作弧，若于点，于点则图中阴影部分的周长为（ ）A. B. C. D. 【答案】C【解析】【分析】由BAC=90，AB=6，AC=8，得又D为BC的中点，有AD= BC=5，根据DMAB，DNAC，BAC=90，知四边形AEDF是矩形，从而可得DE=AC=4，DF=AB=3，即得阴影部分的周长【详解】解：BAC=90，AB=6，AC=8， D为BC的中点， ， DMAB，DNAC，BAC=90， 四边形AEDF是矩形， MDN=90， 是的中位线，DE=AC=4，DF=AB=3，而 阴影部分的周长为故选：C【点睛】本题考查阴影面积，矩形的
15、判定与性质，平行线分线段成比例，三角形的中位线的性质，解题的关键是掌握弧长公式，证明四边形AEDF是矩形7. 如图，在ABC中，D是AC边上的中点，连结BD，把BDC沿BD翻折，得到，DC与AB交于点E，连结，若AD=AC=2，BD=3则点D到BC的距离为（ ）A. B. C. D. 【答案】B【解析】【分析】连接CC，交BD于点M，过点D作DHBC于点H，由翻折知，BDCBDC，BD垂直平分CC，证ADC为等边三角形，利用解直角三角形求出DM=1，CM= =，BM=2，在RtBMC中，利用勾股定理求出BC的长，在BDC中利用面积法求出DH的长.【详解】解：如图，连接CC，交BD于点M，过点D
16、作DHBC于点H，AD=AC=2，D是AC边上的中点，DC=AD=2，由翻折知，BDCBDC，BD垂直平分CC，DC=DC=2，BC=BC，CM=CM，AD=AC=DC=2，ADC为等边三角形，ADC=ACD=CAC=60，DC=DC，DCC=DCC= 60=30，在RtCDM中，DCC=30，DC=2，DM=1，CM=DM= ，.BM=BD-DM=3-1=2，在RtBMC中，BC=.BM=BD-DM=3-1=2,在RtCDM中， 故选B.【点睛】本题考查了轴对称的性质，解直角三角形，勾股定理等，解题关键是会通过面积法求线段的长度.8. 如果一个正整数可以表示为两个连续奇数的平方差，那么称该正
17、整数为“和谐数”如，即8，16均为“和谐数”在不超过2022的正整数中，所有“和谐数”之和等于（ ）A. 255054B. 255064C. 250554D. 255024【答案】D【解析】【分析】由（2n+1）2（2n1）2=8n2022，解得n252，可得在不超过2022的正整数中，“和谐数”共有252个，依此列式计算即可求解【详解】解:由（2n+1）2（2n1）2=8n2022，解得：n252，则在不超过2027的正整数中，所有的“和谐数”之和为3212+5232+50525032=505212=255024故选D【点睛】本题考查了平方差公式，弄清题中“和谐数”的定义是解答本题的关键二、
18、选择题（本题共4小题，每小题3分，共12分在每小题给出的选项中，有多项符合题目要求，全部选对的得3分，有选错的得0分，部分选对的得2分）9. 为了迎接中国共产党第二十次全国代表大会的召开，某班40名学生参加了“党在我心中”知识竞赛，测试成绩如表所示，其中有两个数据被遮盖成绩/分8688909294959698100人数11456515下列关于成绩的统计量中，与被遮盖的数据有关的是（ ）A. 平均数B. 中位数C. 众数D. 方差【答案】AD【解析】【分析】通过计算成绩为86、90分的人数，进行判断，不影响成绩出现次数最多的结果，因此不影响众数，同时不影响找第20、21位数据，因此不影响中位数的
19、计算，进而进行选择【详解】被遮盖部分的人数和为3，众数为100，与被盖的数据无关；中位数应为第20名与第21名成绩和的平均数，为97分，与被盖的数据无关；根据平均数、方差公式知平均数、方差会受到影响故选AD【点睛】本题考查中位数、众数、方差、平均数的意义和计算方法，理解各个统计量的实际意义，以及每个统计量所反应数据的特征，是正确判断的前提10. 如图，AB是圆O的直径，点G是圆上任意一点，点C是的中点，垂足为点E，连接GA，GB，GC，GD，BC，GB与CD交于点F，则下列表述正确的是（ ）A. B. C. D. 【答案】ACD【解析】【分析】根据垂径定理和圆周角定理可以判断A，根据圆周角定理
20、可以判断B，根据圆周角定理、垂径定理以及等角对等边，即可判断C，根据圆周角定理、垂径定理以及平行线的判定，即可判断D【详解】解：AB是圆O的直径，故A正确；AB是圆O的直径，即，也没有其他条件可以证得和的另外一组内角对应相等，不能证得，故B不正确；点C是的中点，AB是圆O的直径，故C正确；点C是的中点，AB是圆O的直径，故D正确故选ACD【点睛】本题主要考查了垂径定理、圆周角定理、等腰三角形的判定以及平行线的判定11. 下表中列出的是一个二次函数的自变量与函数的几组对应值：0136下列各选项中，正确的是（ ）A. 函数图象的开口向下B. 当时，的值随的增大而增大C. 函数的图象与轴无交点D.
21、这个函数的最小值小于【答案】BD【解析】【分析】根据抛物线经过点（0，-4），（3，-4）可得抛物线对称轴为直线，由抛物线经过点（-2，6）可得抛物线开口向上，进而求解【详解】解：抛物线经过点（0，-4），（3，-4）， 抛物线对称轴为直线， 抛物线经过点（-2，6）， 当x时，y随x增大而减小， 抛物线开口向上，且跟x轴有交点，故A，C错误，不符合题意； x时，y随x增大而增大，故B正确，符合题意； 由对称性可知，在处取得最小值，且最小值小于-6故D正确，符合题意 故选：BD【点睛】本题考查二次函数的图象与性质，解题关键是掌握二次函数与方程的关系12. 如图，正方形的边长为8，点，分别在边，
22、上，将正方形沿折叠，使点落在边上的处，点落在处，交于下列结论正确的是（ ）A. 当为中点时，B. 当时，C. 当（点不与、重合）在上移动时，周长随着位置变化而变化D. 连接，则【答案】ABD【解析】【分析】当为CD中点时，设则，由勾股定理列方程求解，进一步求得的值，进而可判断A的正误；当三边之比为3：4：5时，设，由可求a 的值，进一步求得的值，进而可判断B的正误；过点A作，垂足为H，连接，AG，先证，可得，再证，可得，由此证得周长16，进而可判断C的正误；过点E作EMBC，垂足为M，连接交EM，EF于点N，Q，证明，进而可判断D的正误【详解】：为CD中点，正方形ABCD的边长为8，由折叠的性
23、质，设则，在中，由勾股定理得，即42+（8x）2x2，解得x5，AE5，DE3，故A正确；当三边之比为3：4：5时，设，则，解得：，故B正确；过点A作，垂足为H，连接，AG，则，由折叠的性质可知，在和中，在与中，周长，当在CD上移动时，周长不变，故C错误；如图，过点E作EMBC，垂足为M，连接交EM，EF于点N，Q，由翻折可知：EF垂直平分，在和中， ，故D正确故选：ABD【点睛】本题考查了正方形的性质，折叠的性质，勾股定理，全等三角形的判定与性质等知识解题的关键在于对知识的熟练掌握与灵活运用第卷（非选择题，84分）三、填空题（本题共4小题，共12分，只要求填写最后结果，每小题填对得3分）13
24、. 若一次函数的图象经过第一、二、四象限，则化简_【答案】【解析】【分析】首先根据一次函数的位置确定a和b的值，然后化简二次根式求值【详解】解：若一次函数y=ax+b图象经过第一、二、四象限，a0，b0，b-a0， ，故答案为-b【点睛】本题主要考查一次函数和图象和性质，熟记一次函数的图象和性质是解题的关键14. 若，是一元二次方程的两个实数根，则的值是_【答案】31【解析】【分析】根据根与系数的关系得到，再根据完全平方公式变形即可求解【详解】根据根与系数的关系得，所以故答案为：31【点睛】此题主要考查根与系数的关系，解题的关键是熟知完全平方公式的变形运用15. 如图，函数和的图像分别是和设点
25、在上，轴交于点，轴交于点，的面积_【答案】【解析】【分析】设点，则点，得到，的长，最后求得的面积【详解】解：设点，则点，故答案为：【点睛】本题考查了反比例函数的图像上点的坐标特征，直角三角形的面积，解题的关键是熟知反比例函数图像上点的坐标的特征16. 如图，已知的内角，分别作内角与外角的平分线，两条平分线交于，得；和的平分线交于，得；，以此类推得到，则_（用表示）【答案】【解析】【分析】先根据角平分线的定义、三角形的外角性质分别求出和，再归纳类推出一般规律，由此即可得【详解】解：分别平分，同理可得：，归纳类推得：，其中为正整数，则，故答案为：【点睛】本题考查了角平分线的定义、三角形的外角性质，
26、正确归纳类推出一般规律是解题关键四、解答题（本题共7小题，共72分解答应写出必要文字说明或演算步骤）17. 某校为了“中考体测”的顺利进行，引导同学们积极参加体育锻炼，学校购买了一批跳绳供学生借用，现从九年级随机抽取了部分学生对新跳绳进行测试，绘制了如下的两幅不完整的统计表和统计图请根据相关信息，解答下列问题：一分钟跳绳成绩的分组统计表 组别跳绳次数分段频数A10BC42D13一分钟跳绳成绩的扇形统计图（1）本次接受随机抽样调查的学生人数为 人，统计表中的的值为 ；（2）抽取学生一分钟跳绳成绩的中位数所在的组别是 ；（3）现在指定两名男生和两名女生负责跳绳发放和整理工作，若两人一组，随机组合，
27、则恰好分组都是一男一女的概率是多少？【答案】（1）100 ，35 （2）C （3）恰好分组都是一男一女的概率是【解析】【分析】（1）将A组的频数除以扇形所占的百分比即可求出学生总数，再将总数减去A、C、D的频数即可求出m；（2）由（1）可知学生总数为100人，按顺序排列后，中位数应该是55和56两个数的平均数，A组是10人，B组为35人，即可得答案；（3）通过列表即可分析出分组都是一男一女的概率【小问1详解】解：学生总数为：1010%=100，m=100-10-42-13=35，故答案是：100，35；【小问2详解】A、B、C、D组已经按顺序排列，学生总数为100人，A组是10人，B组为35人
28、，中位数应该是第51个数和第52个数的平均数，中位数在C组；【小问3详解】根据题意列表男1男2女1女2男1男2，男1女1，男1女2，男1男2男1，男2女1，男2女2，男2女1男1，女1男2，女1女2，女1女2男1，女2男2，女2女1，女2由上表可知，共有12种情况，并且它们出现的机会均等，其中都是一男一女的有8种， 所以，【点睛】本题考查了频数，中位数和概率的求法，解题的关键是列出表格求概率18. 自“新冠”病毒出现后，瓶装酒精成了人们家中常备之物一种酒精消毒瓶如图1，AB为喷嘴，BCD为按压柄，CE为伸缩连杆，BE和EF为导管，其示意图如图2，DBEBEF108，BD6cm，BE4cm当按压
29、柄BCD按压到底时，BD转动到，此时EF（如图3）（1）求BD转动到扫过的面积（结果保留）；（2）求点D到直线EF的距离（结果精确到0.1cm）（参考数据：sin360.59，cos360.81，tan360.73，sin720.95，cos720.31，tan723.08）【答案】（1）cm2 （2）7.3cm【解析】【分析】（1）根据平行线的性质可求出，从而求出，然后根据扇形的面积计算公式即可解答；（2）过点D作，垂足为G，过点E作，垂足为H，分别在RtBDG和RtBHE中，利用锐角三角函数的定义求出DG，EH的长，进行计算即可解答【小问1详解】解：BDEF，BEF108，180BEF72
30、，DBE108，DBE1087236，BD6cm，BD转动到扫过的面积（cm2），BD转动到扫过的面积为cm2；【小问2详解】解：过点D作，垂足为G，过点E作，垂足为H，在RtBDG中，DBG36，DGBDsin3660.593.54（cm），在RtBHE中，EBH72，EHBEsin7240.953.80（cm），DG+EH3.54+3.807.3（cm），点D到直线EF的距离为7.3cm【点睛】本题考查了解直角三角形的应用、扇形的面积、平行线的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键19. 数学是一个不断思考，不断发现，不断归纳的过程，古希腊数学家帕普斯（Pappus
31、，约300350）把三等分的操作如下：以点为坐标原点，所在的直线为轴建立平面直角坐标系；在平面直角坐标系中，绘制反比例函数的图象，图象与的边交于点；以点为圆心，为半径作弧，交函数图象于点；分别过点和作轴和轴的平行线，两线交于点，；作射线，交于点，得到（1）任务一：判断四边形的形状，并证明；（2）任务二：请证明【答案】（1）矩形，证明见解析 （2）见解析【解析】【分析】（1）根据题意可知，由此即可证明四边形是矩形；（2）先证明，则，再由推出推出即可得到则【小问1详解】解： 结论：四边形是矩形证明：分别过点和作轴和轴的平行线，两线交于点，四边形是平行四边形，四边形是矩形【小问2详解】证明：矩形的对
32、角线与相交于点，是的外角，以点为圆心，为半径作弧，交函数的图象于点，【点睛】本题主要考查了矩形的性质与判定，坐标与图形，反比例函数与几何综合，等腰三角形的性质与判定，三角形外角的性质等等，正确理解题意是解题的关键20. 点M，N为正方形ABCD平面内两点，BMBN（1）如图1，点M为边CD上一点，D，A，N三点共线求证：BMBN（2）如图2，点M为正方形ABCD外一点，CMMN，M，A，N三点共线BMBN是否仍然成立，请说明理由（3）在（2）的条件下，若CM1，BN4，求正方形的边长【答案】（1）见解析 （2）成立，理由见解析 （3）【解析】【分析】（1）从是正方形，得到， 从，得到，得到，推
33、出，推出（2）仍然成立：从是正方形，推出，从，推出，从，推出从，推出，推出，得到（3）连接，从，推出，得到，由勾股定理，推出【小问1详解】证明：如图1，是正方形，【小问2详解】解：仍然成立，理由如下：如图2，是正方形，【小问3详解】解：如图2，连接由（2），由勾股定理，【点睛】本题主要考查了正方形，三角形全等，勾股定理，解决问题的关键是熟练掌握正方形的边角性子，全等三角形的判定和性质，熟练运用勾股定理21. 如图，是某同学正在设计一动画示意图，轴上依次有，三个点，且，在上方有五个台阶（各拐角均为），每个台阶的高、宽分别是1和1.5，台阶到轴距离从点处向右上方沿抛物线发出一个带光的点（1）求点的
34、横坐标，且在图中补画出轴，并直接指出点会落在哪个台阶上；（2）当点落到台阶上后立即弹起，又形成了另一条与形状相同的抛物线，且最大高度为11，求抛物线的表达式【答案】（1）点的横坐标为；作图见解析；点会落在台阶上 （2）【解析】【分析】（1）由题意台阶的左边端点，右边端点的坐标，求出，6时的的值，即可判断；（2）由题意抛物线，经过，最高点的纵坐标为11，构建方程组求出，可得结论【小问1详解】解：图形如图所示， 由题意台阶左边的端点坐标，右边的端点，对于抛物线，令，解得或6，点的横坐标为，当时，当时，当时，解得或5，抛物线与台阶有交点，设交点为，点会落在台阶上；【小问2详解】解：由题意抛物线，经过
35、，最高点的纵坐标为11，解得或（舍弃），抛物线的解析式为【点睛】本题属于二次函数综合题，考查了二次函数的性质，待定系数法等知识，解题的关键是学会寻找特殊点解决问题，属于中考压轴题22. 如图，上有，三点，是直径，点是的中点，连接交于，在延长线上，且（1）求证：是的切线；（2）若，求的半径和的值【答案】（1）证明见解析 （2）半径为；【解析】【分析】（1）根据可得，根据点是弧的中点得到，证明，进而得到，即可证明是的切线；（2）在中，根据，即可求出，在中，即可求出的半径；连接，证明即可得到的值【小问1详解】证明：，点是弧的中点， 是直径，即，是的切线； 【小问2详解】解：，令，则，解得， 在中，半
36、径为； 在中， ，连接， 【点睛】本题主要考查了切线的判定、解直角三角形、勾股定理、相似三角形的判定与性质等知识；熟练掌握切线的判定和解直角三角形是解题的关键23. 综合与探究如图，抛物线与轴交于，两点，与轴交于点，点，的坐标分别为(2，0)，(0，3)，点与点关于轴对称，是直线上方抛物线上一动点，连接、交于点（1）求抛物线的函数表达式及点的坐标；（2）在点运动的过程中，求：的最大值；（3）在轴上是不存在点，使？若存在，请直接写出点的坐标；若不存在，请说明理由【答案】（1），A(-3，0)； （2）； （3）存在，M(0，6)或(0，-6)，理由见解析【解析】【分析】（1）将，两点坐标代入抛物
37、线的函数表达式求得，进而抛物线函数表达式，根据抛物线对称性或令，进而求得结果；（2）作于，交于，设出点和点坐标，表示出的长，根据列出比例式，进而配方，进一步求得结果；（3）可先求在轴正半轴时：以为底作等腰直角三角形，以为圆心，为半径作圆，交轴于，设点M(0，m)，由列出方程求得的值，从而求得坐标，根据对称性求得再轴负半轴的情形【小问1详解】把点，的坐标代入得，解得，由得，舍去，A(-3，0)；【小问2详解】如图， 作于，交于，设直线AC的解析式为 把A(-3，0)，C(0，3)代入得， 解得， 直线的关系式是：，设，点与点关于轴对称，当时，；【小问3详解】如图， 以为底作等腰直角三角形，以为圆心，为半径作圆，交轴于，设点M(0，m)，舍去，(0，6)，由对称性可得：(0，-6)，综上所述：M(0，6)或(0，-6)【点睛】本题考查了二次函数及其图象性质，相似三角形的判定和性质，确定圆的条件，等腰直角三角形性质等知识，解决问题的关键是熟练掌握“定弦对定角”模型
