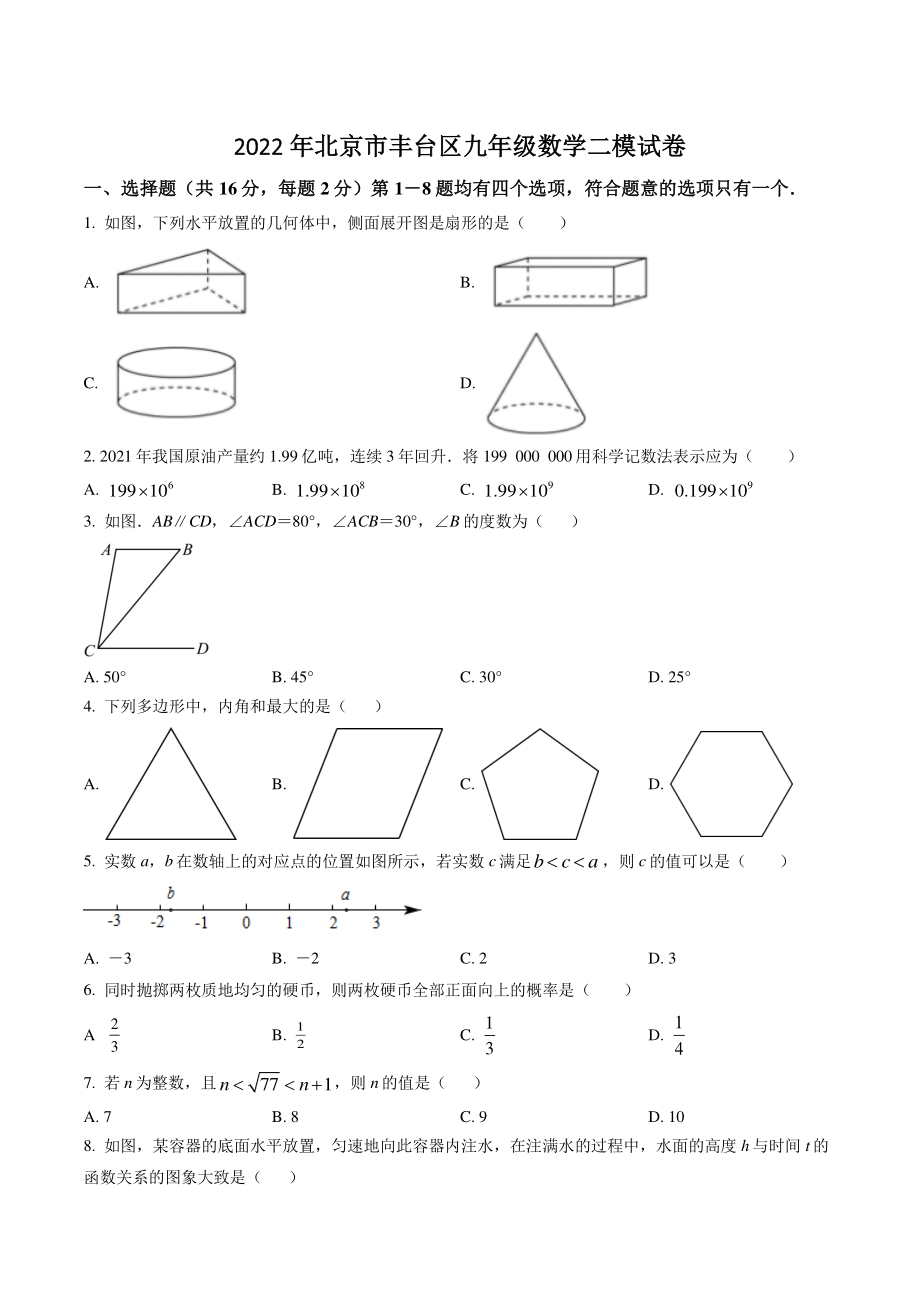
1、20222022 年北京市丰台区九年级数学二模试年北京市丰台区九年级数学二模试卷卷 一、选择题（共一、选择题（共 16 分，每题分，每题 2 分）第分）第 18 题均有四个选项，符合题意的选项只有一个题均有四个选项，符合题意的选项只有一个 1. 如图，下列水平放置的几何体中，侧面展开图是扇形的是（ ） A. B. C. D. 2. 2021 年我国原油产量约 1.99亿吨，连续 3 年回升将 199 000 000用科学记数法表示应为（ ） A. 6199 10 B. 81.99 10 C. 91.99 10 D. 90.199 10 3. 如图ABCD，ACD80 ，ACB30 ，B 的度数
2、为（ ） A. 50 B. 45 C. 30 D. 25 4. 下列多边形中，内角和最大的是（ ） A. B. C. D. 5. 实数 a，b在数轴上的对应点的位置如图所示，若实数 c满足bca，则 c 的值可以是（ ） A. 3 B. 2 C. 2 D. 3 6. 同时抛掷两枚质地均匀的硬币，则两枚硬币全部正面向上的概率是（ ） A 23 B. 12 C. 13 D. 14 7. 若 n 为整数，且771nn，则 n的值是（ ） A. 7 B. 8 C. 9 D. 10 8. 如图，某容器的底面水平放置，匀速地向此容器内注水，在注满水的过程中，水面的高度 h与时间 t的函数关系的图象大致是（
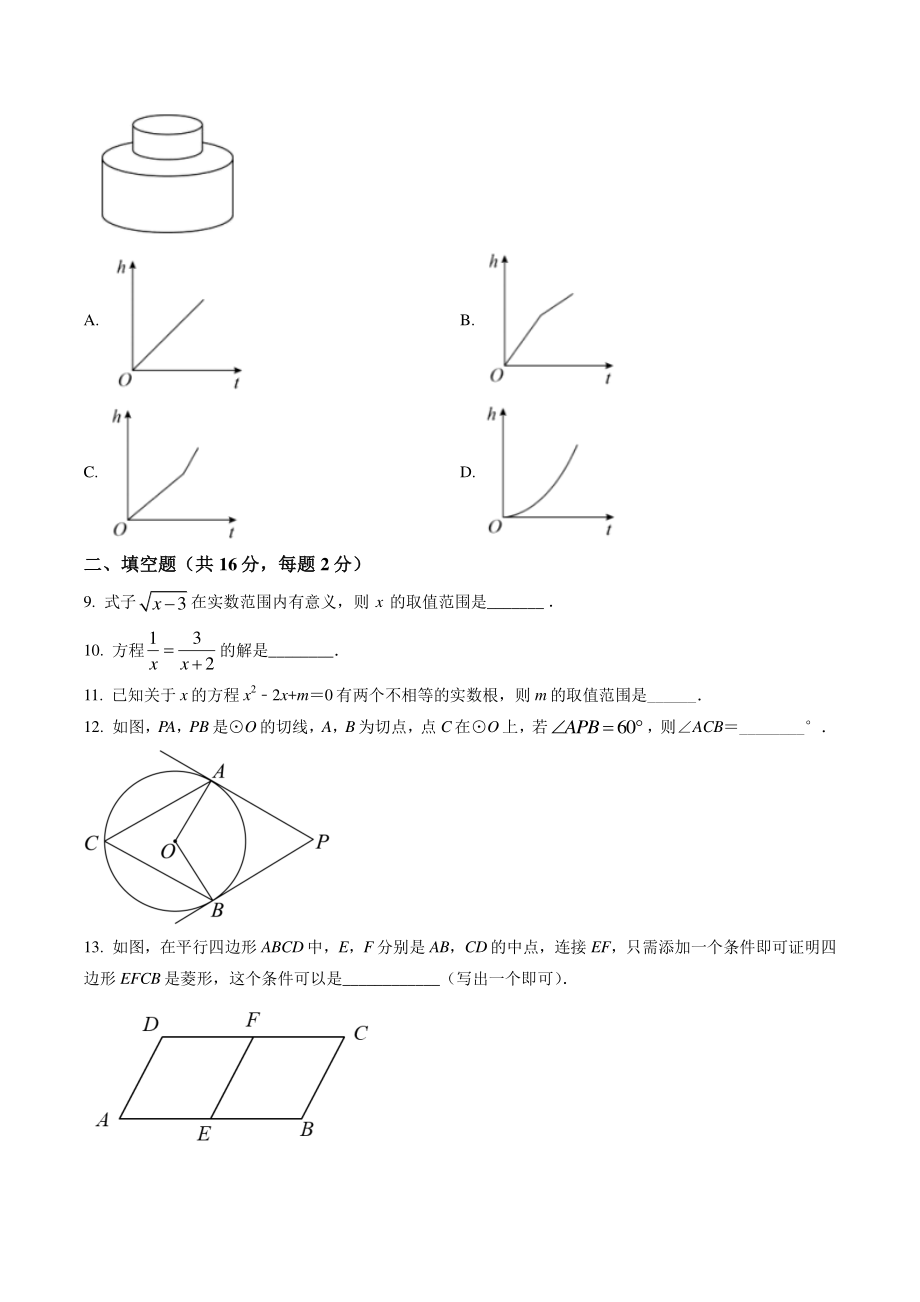
3、 ） A. B. C. D. 二、填空题（共二、填空题（共 16 分，每题分，每题 2 分）分） 9. 式子3x在实数范围内有意义，则 x 的取值范围是_ 10. 方程132xx的解是_ 11. 已知关于 x 的方程 x22x+m0有两个不相等的实数根，则 m 的取值范围是_ 12. 如图，PA，PB 是O的切线，A，B为切点，点 C在O上，若60APB，则ACB_ 13. 如图，在平行四边形 ABCD 中，E，F 分别是 AB，CD 的中点，连接 EF，只需添加一个条件即可证明四边形 EFCB 是菱形，这个条件可以是_（写出一个即可） 14. 在直角坐标系xOy中，直线yx与双曲线0mymx
4、交于A，B两点若点A，B的横坐标分别为1x，2x，则12xx的值为_ 15. 甲、乙两台包装机同时包装糖果，分别从中随机抽取 5袋，测得它们的实际质量（单位：g）如下表所示： 甲 100 102 99 101 98 乙 100 97 104 97 102 那么_包装机包装的 5袋糖果的质量比较稳定（填“甲”或“乙”） 16. 某超市现有 n个人在收银台排队等候结账设结账人数按固定的速度增加，收银员结账的速度也是固定的若同时开放 2个收银台，需要 20分钟可使排队等候人数为 0；若同时开放 3个收银台，需要 12 分钟可使排队等候人数为 0为减少顾客等待结账的时间，需要 6 分钟内使排队等候人数
5、为 0，则需要至少同时开放_个收银台 三、解答题（共三、解答题（共 68 分，第分，第 1720 题，每题题，每题 5 分，第分，第 21 题题 6 分，第分，第 22 题题 5 分，第分，第 2324 题题每题每题 6 分，第分，第 25题题 5 分，第分，第 26 题题 6 分，第分，第 2728 题，每题题，每题 7 分）解答应写出文字说明、演分）解答应写出文字说明、演算步骤或证明过程算步骤或证明过程 17. 计算：032sin4583 18. 解不等式组：2323212xxxx 19. 已知22320ab，求代数式22aba ab值 20. 已知：如图，射线 AM 求作：ABC，使得9
6、0ABC，30BAC 作法：在射线 AM 上任取一点 O（不与点 A重合） ； 以点 O 为圆心，OA 长为半径画弧，交射线 AM于 A，C 两点； 以点 C 为圆心，CO长为半径画弧，交AC于点 B； 连接 AB，BC ABC 就是所求作的三角形 （1）使用直尺和圆规，依作法补全图形（保留作图痕迹） ； （2）完成下面的证明： 证明：连接 OB 在O中，OBOC 在C中，OCBC OBOCBC OCB是等边三角形 60ACB AC是O的直径， ABC_ （_） （填推理的依据） 90ACBBAC 30BAC 21. 如图，在ABC中，90BAC，ADBC，垂足为 D，AEBC，CEDA （1
7、）求证：四边形 AECD是矩形； （2）若 AB5，3cos5B ，求 AE的长 22. 在平面直角坐标系 xOy 中， 一次函数0ykxb k图象由函数yx的图象向下平移 4个单位长度得到 （1）求这个一次函数的解析式； （2）一次函数ykxb的图象与 x轴的交点为 A，函数(0)ymx m的图象与一次函数ykxb的图象的交点为 B，记线段 OA，AB，BO围成的区域（不含边界）为 W，横、纵坐标都是整数的点叫做整点，若区域 W内恰有 2 个整点，直接写出 m的取值范围 23. 如图，AB 是O 的直径，C 为 BA延长线上一点，过点 C作O的切线，切点为 D，过点 B 作 BECD于点 E
8、，连接 AD，BD （1）求证：ABDDBE； （2）如果 CAAB，BD4，求 BE 的长 24. 跳台滑雪是冬季奥运会比赛项目之一 记运动员在该项目的运动过程中的某个位置与起跳点的水平距离为 x（单位：m） ，竖直高度为 y（单位：m） ，下面记录了甲运动员起跳后的运动过程中的七组数据： x/m 0 10 20 30 40 50 60 y/m 54.0 57.8 57.6 53.4 45.2 33.0 16.8 下面是小明的探究过程，请补充完整： （1）为观察 y 与 x 之间的关系，建立坐标系，以 x为横坐标，y为纵坐标，描出表中数据对应的 7 个点，并用平滑的曲线连接它们： （2）观察
9、发现， （1）中的曲线可以看作是_的一部分（填“抛物线”或“双曲线”） ，结合图象，可推断出水平距离约为_m（结果保留小数点后一位）时，甲运动员起跳后达到最高点； （3）乙运动员在此跳台进行训练，若乙运动员在运动过程中的最高点的竖直高度达到 61m，则乙运动员运动中的最高点比甲运动员运动中的最高点_（填写“高”或“低”）约_m（结果保留小数点后一位） 25. 2022年是中国共产主义青年团建团 100周年，某校团委组织七、八年级学生开展主题为“成团百年，勇当先锋”的团史知识学习活动，为了解这两个年级学生团史知识的学习情况，从七、八年级的学生中，各随机抽取了 20名学生进行测试，获得了他们的成绩
10、（百分制，且成绩均为整数） ，并对数据（成绩）进行了整理、描述和分析，下面给出了部分信息 a 该校七年级抽取学生测试成绩的数据的频数分布直方图如下 （数据分为 5 组7580y，8085y，8590 x，9095y，95100y） b该校七年级抽取的学生测试成绩的数据在8590 x这一组的是：85；85；85；86；87；88 c该校七、八年级抽取的学生的测试成绩的数据的平均数、中位数、众数如下： 平均数 中位数 众数 七年级 85.2 m 85 八年级 87 89.5 90 根据以上信息，回答下列问题： （1）写出表中 m的值； （2）此次测试成绩 90分及 90 分以上为优秀 记该校七年级
11、抽取的学生中成绩优秀的人数是1x，八年级抽取的学生中成绩优秀的人数为2x，比较1x，2x的大小，并说明理由； 该校七、八年级各有 200 名学生，假设该校七、八年级学生全部参加此次测试，请估计成绩优秀的学生总人数（直接写出结果） 26. 在平面直角坐标系 xOy 中，已知抛物线223yxax （1）求该抛物线的对称轴（用含 a的式子表示） （2）11A xy，22B xy，为该抛物线上的两点，若112xa ，21xa，且12yy，求 a 的取值范围 27. 如图， 在ABC 中， ABAC， BAC120， D是 BC中点， 连接 AD 点 M 在线段 AD 上 （不与点 A，D 重合） ，连
12、接 MB，点 E在 CA的延长线上且 MEMB，连接 EB （1）比较ABM与AEM 的大小，并证明； （2）用等式表示线段 AM，AB，AE 之间的数量关系，并证明 28. 在平面直角坐标系 xOy 中， O的半径为 1， A 为任意一点， B为O上任意一点， 给出如下定义： 记 A，B 两点间的距离的最小值为 p（规定：点 A在O上时，0p ） ，最大值为 q，那么把2pq的值称为点 A与O的“关联距离”，记作 d（A，O） （1）如图，点 D，E，F的横、纵坐标都是整数 d（D，O）_； 若点 M在线段 EF上，求 d（M，O）取值范围； （2）若点 N在直线32 3yx上，直接写出 d
13、（N，O）的取值范围； （3） 正方形的边长为 m， 若点 P在该正方形的边上运动时， 满足 d （P， O） 的最小值为 1， 最大值为10，直接写出 m的最小值和最大值 20222022 年北京市丰台区九年级数学二模试年北京市丰台区九年级数学二模试卷卷 一、选择题（共一、选择题（共 16 分，每题分，每题 2 分）第分）第 18 题均有四个选项，符合题意的选项只有一个题均有四个选项，符合题意的选项只有一个 1. 如图，下列水平放置的几何体中，侧面展开图是扇形的是（ ） A. B. C. D. 【答案】D 【解析】 【分析】侧面展开图是把一个立方体从其侧面竖直剪开，展开后的那个平面即为侧面展
14、开图，据此逐一判断即可得答案 【详解】解：A、侧面展开图是矩形，故此选项不合题意； B、侧面展开图是矩形，故此选项不合题意； C、侧面展开图是矩形，故此选项不符合题意； D、侧面展开图是扇形，故此选项符合题意； 故选：D 【点睛】本题考查几何体的侧面展开图，侧面展开图是把一个立方体从其侧面竖直剪开，展开后的那个平面即为侧面展开图，解题关键理解侧面展开图的定义 2. 2021 年我国原油产量约 1.99亿吨，连续 3 年回升将 199 000 000用科学记数法表示应为（ ） A. 6199 10 B. 81.99 10 C. 91.99 10 D. 90.199 10 【答案】B 【解析】 【
15、分析】将一个数表示成10na的形式，其中110a，n为整数，这种记数的方法叫做科学记数法，根据科学记数法的定义即可得 【详解】81990000001.99 10 故选：B 【点睛】 本题考查了科学记数法， 熟记科学记数法的定义 （将一个数表示成10na的形式， 其中110a，n为整数，这种记数的方法叫做科学记数法）是解题关键确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同 3. 如图ABCD，ACD80 ，ACB30 ，B 的度数为（ ） A. 50 B. 45 C. 30 D. 25 【答案】A 【解析】 【分析】首先求出50BCD，然后根据平行线的性质
16、直接得出50BBCD 【详解】80ACD，30ACB， 50BCDACDACB， /ABCD， 50BBCD 故选：A 【点睛】本题考查角度的计算，解题的关键是熟练掌握平行线的性质 4. 下列多边形中，内角和最大的是（ ） A. B. C. D. 【答案】D 【解析】 【分析】根据多边形的内角和公式求解即可 【详解】解：多边形的内角和21803nn，n 代表多边形的边数， 多边形的边数 n越大，内角和越大， 3 4 5 6 ， 六边形的内角和最大 故选：D 【点睛】本题主要考查了多边形的内角和公式：21803nn，熟记多边形的内角和公式是解题的关键 5. 实数 a，b在数轴上的对应点的位置如图
17、所示，若实数 c满足bca，则 c 的值可以是（ ） A. 3 B. 2 C. 2 D. 3 【答案】C 【解析】 【分析】根据bca结合数轴判断，即可得 c的值 【详解】解：由数轴及bca知，c的取值只能是-1，0，1，2这四个整数， 观察四个选项，只有选项 C符合 故选：C 【点睛】 本题考查了在数轴比较大小， 牢记数轴上左边的的点表示的数小于右边的点表示的数是解题关键 6. 同时抛掷两枚质地均匀的硬币，则两枚硬币全部正面向上的概率是（ ） A. 23 B. 12 C. 13 D. 14 【答案】D 【解析】 【分析】画出树状图，从而可得同时抛掷两枚质地均匀的硬币的所有等可能的结果，再找出
18、两枚硬币全部正面向上的结果，然后利用概率公式计算即可得 【详解】解：由题意，画树状图如下： 由图可知，同时抛掷两枚质地均匀的硬币的所有等可能的结果共有 4种，其中，两枚硬币全部正面向上的结果有 1种， 则两枚硬币全部正面向上的概率是14P ， 故选：D 【点睛】本题考查了利用列举法求概率，正确画出树状图是解题关键 7. 若 n 为整数，且771nn，则 n的值是（ ） A. 7 B. 8 C. 9 D. 10 【答案】B 【解析】 【分析】根据 n 为整数，647781，即可求得 n的值 【详解】解：647781， 8779， n为整数，且771nn， n=8 故选：B 【点睛】本题主要考查了
19、无理数的估算，熟练掌握无理数估算的方法是解题的关键 8. 如图，某容器的底面水平放置，匀速地向此容器内注水，在注满水的过程中，水面的高度 h与时间 t的函数关系的图象大致是（ ） A. B. C. D. 【答案】C 【解析】 【分析】根据图象可知，物体的形状为首先大然后变小故注水过程的水的高度是先慢后快 【详解】解：相比较而言，注满下面圆柱体，用时较多，高度增加较慢，注满上面圆柱体，用时较少，高度增加较快， 所以选项 C的图像符合此图 故选：C 【点睛】本题考查函数的图象，解题的关键是理解题意，灵活运用所学知识解决问题 第二部分第二部分 非选择题非选择题 二、填空题（共二、填空题（共 16 分
20、，每题分，每题 2 分）分） 9. 式子3x在实数范围内有意义，则 x 的取值范围是_ 【答案】x3 【解析】 【分析】直接利用二次根式有意义的条件得到关于 x 的不等式，解不等式即可得答案. 【详解】由题意可得：x30， 解得：x3， 故答案为 x3 【点睛】本题考查了二次根式有意义的条件，熟练掌握二次根式的被开方数是非负数是解题的关键. 10. 方程132xx的解是_ 【答案】x=1 【解析】 【详解】132xx， x+2=3x， x=1， 检验：当 x=1 时，x（x+2）0， 原方程的解为 x=1 故答案为 x=1 11. 已知关于 x 的方程 x22x+m0有两个不相等的实数根，则
21、m 的取值范围是_ 【答案】m1 【解析】 【分析】关于 x的方程 x22x+m0 有两个不相等的实数根，即判别式 b24ac0即可得到关于 m的不等式，从而求得 m的范围 【详解】解：a1，b2，cm， b24ac（2）24 1 m44m0， 解得：m1 故答案为 m1 【点睛】本题考查了一元二次方程根的判别式，掌握一元二次方程根的判别式是解题的关键 12. 如图，PA，PB 是O的切线，A，B为切点，点 C在O上，若60APB，则ACB_ 【答案】60 【解析】 【分析】先根据圆的切线的性质可得90OAPOBP，再根据四边形的内角和可得120AOB，然后根据圆周角定理即可得 【详解】解：,
22、PA PB是O的切线， 90OAPOBP ， 60APB， 360120AOBOAPOBPAPB， 由圆周角定理得：1602ACBAOB， 故答案为：60 【点睛】本题考查了圆的切线的性质、圆周角定理等知识点，熟练掌握圆的切线的性质和圆周角定理是解题关键 13. 如图，在平行四边形 ABCD 中，E，F 分别是 AB，CD 的中点，连接 EF，只需添加一个条件即可证明四边形 EFCB 是菱形，这个条件可以是_（写出一个即可） 【答案】BCBE（答案不唯一） 【解析】 【分析】先根据平行四边形的性质可得,ABCD AB CD，再根据线段中点的定义可得1122CFCDABBE，然后根据平行四边形的
23、判定可得四边形EFCB是平行四边形，最后根据菱形的判定即可得出答案 【详解】解：四边形ABCD是平行四边形， ,ABCD AB CD， ,E F分别是,AB CD的中点， 1122CFCDABBE， 四边形EFCB是平行四边形， 要使四边形EFCB是菱形，添加的这个条件可以是BCBE， 故答案为：BCBE（答案不唯一） 【点睛】本题考查了平行四边形的判定与性质、菱形的判定，熟练掌握菱形的判定是解题关键 14. 在直角坐标系xOy中，直线yx与双曲线0mymx交于A，B两点若点A，B的横坐标分别为1x，2x，则12xx的值为_ 【答案】0 【解析】 【分析】根据“正比例函数与反比例函数的交点关于
24、原点对称”即可求解. 【详解】解：正比例函数和反比例函数均关于坐标原点 O 对称， 正比例函数和反比例函数的交点亦关于坐标原点中心对称， 120 xx， 故答案为：0. 【点睛】本题考查正比例函数和反比例函数的图像性质，根据正比例函数与反比例函数的交点关于原点对称这个特点即可解题. 15. 甲、乙两台包装机同时包装糖果，分别从中随机抽取 5袋，测得它们的实际质量（单位：g）如下表所示： 甲 100 102 99 101 98 乙 100 97 104 97 102 那么_包装机包装的 5袋糖果的质量比较稳定（填“甲”或“乙”） 【答案】甲 【解析】 【分析】分别求出甲和乙的平均数及方差，再比较
25、即可 【详解】1(100 10299 101 98)1005x甲，1(10097 10497 102)1005x乙， 2222221(100 100)(102 100)(99 100)(101 100)(98 100)25S甲， 2222221(100 100)(97 100)(104 100)(97 100)(102 100)7.65S乙， 22SS甲乙， 甲包装机包装的 5袋糖果的质量比较稳定， 故答案为：甲 【点睛】本题考查了平均数和方差及其意义，熟练掌握公式是解题的关键 16. 某超市现有 n个人在收银台排队等候结账设结账人数按固定的速度增加，收银员结账的速度也是固定的若同时开放 2个
26、收银台，需要 20分钟可使排队等候人数为 0；若同时开放 3个收银台，需要 12 分钟可使排队等候人数为 0为减少顾客等待结账的时间，需要 6 分钟内使排队等候人数为 0，则需要至少同时开放_个收银台 【答案】6 【解析】 【分析】设每分钟增加结账人数 x人，每分钟收银员结账 y人，根据题意，得 y=2x，n=60 x根据为减少顾客等待结账的时间，需要 6 分钟内使排队等候人数为 0的要求，可设开放 a个收银台，则 6ay6x+n，将 y和 n代入，即可求得 a 的取值，从而请求解 【详解】解：设每分钟增加结账人数 x人，每分钟收银员结账 y人，根据题意，得 202 20123 12xnyxn
27、y 化简，得 y=2x，n=60 x， 为减少顾客等待结账的时间，需要 6分钟内使排队等候人数为 0， 设开放 a个收银台，则 6ay6x+n， 即 6a2x6x+60 x， 12a66， x0， a112， a是正整数， a6， 需要至少同时开放 6个收银台 故答案：6 【点睛】本题考查了二元一次方程组和不等式的应用，弄清题意，正确设未知数找到相等关系是解题的关键 三、解答题（共三、解答题（共 68 分，第分，第 1720 题，每题题，每题 5 分，第分，第 21 题题 6 分，第分，第 22 题题 5 分，第分，第 2324 题题每题每题 6 分，第分，第 25题题 5 分，第分，第 26
28、 题题 6 分，第分，第 2728 题，每题题，每题 7 分）解答应写出文字说明、演分）解答应写出文字说明、演算步骤或证明过程算步骤或证明过程 17. 计算：032sin4583 【答案】42 【解析】 【分析】原式第一项利用绝对值意义化简，第二项利用特殊角的三角函数值计算，第三项化为最简二次根式，第四项利用零指数幂法则计算即可得到结果 【详解】解：原式 = 2322 2 12-?+ =322 2 1-+ =42 【点睛】此题考查了实数的运算，熟练掌握运算法则是解本题的关键 18. 解不等式组：2323212xxxx 【答案】14x 【解析】 【分析】先求出每个不等式的解集，然后取公共部分即可
29、得到答案 【详解】解：原不等式组为2323212xxxx， 由得：1x ， 由得：4x， 所以原不等式组的解集为：14x 【点睛】本题考查了解一元一次不等式组，解题的关键是熟练掌握解不等式 19. 已知22320ab，求代数式22aba ab的值 【答案】2 【解析】 【分析】先将22320ab变形，得出2232ab，再将原式利用完全平方公式和整式运算化简，即可求解 【详解】22320ab， 2232ab， 222222222232aba abaabbaabab 【点睛】本题考查了完全平方公式和整式的化简求值，熟练掌握知识点是解题的关键 20. 已知：如图，射线 AM 求作：ABC，使得90A
30、BC，30BAC 作法：在射线 AM 上任取一点 O（不与点 A重合） ； 以点 O 为圆心，OA 长为半径画弧，交射线 AM于 A，C 两点； 以点 C圆心，CO长为半径画弧，交AC于点 B； 连接 AB，BC ABC 就是所求作的三角形 （1）使用直尺和圆规，依作法补全图形（保留作图痕迹） ； （2）完成下面的证明： 证明：连接 OB 在O中，OBOC 在C中，OCBC OBOCBC OCB是等边三角形 60ACB AC是O的直径， ABC_ （_） （填推理的依据） 90ACBBAC 30BAC 【答案】 （1）见解析 （2）90，直径所对的圆周角是直角 【解析】 【分析】 （1）根据要
31、求作出图形即可； （2）证明OCB是等边三角形，求出ABC90 即可 【小问 1 详解】 解：如图，ABC即为所作； 【小问 2 详解】 证明：连接 OB 在O中，OBOC， 在C中，OCBC， OBOCBC， OCB是等边三角形， 60ACB， AC是O的直径， ABC90 （直径所对的圆周角是直角） ， 90ACBBAC， 30BAC 故答案为：90，直径所对的圆周角是直角 【点睛】本题考查作图复杂作图，等边三角形的判定和性质，直径所对的圆周角是直角，解题的关键是理解题意，灵活运用所学知识解决问题 21. 如图，在ABC中，90BAC，ADBC，垂足为 D，AEBC，CEDA （1）求证：
32、四边形 AECD是矩形； （2）若 AB5，3cos5B ，求 AE的长 【答案】 （1）见详解 （2）163 【解析】 【分析】 （1）先证四边形 AECD 是平行四边形，再证是矩形即可； （2）根据锐角三角函数进行求解即可； 【小问 1 详解】 证明：AEBC，CEDA 四边形 AECD是平行四边形 ADBC AECD是矩形 【小问 2 详解】 90BAC，ADBC 3cos5ABBDBBCAB AB5 253BC ，3BD 根据矩形的性质， 2516333AECDBCBD 【点睛】本题主要考查矩形的性质、锐角三角函数，掌握相关知识并灵活应用是解题的 22. 在平面直角坐标系 xOy 中，
33、 一次函数0ykxb k的图象由函数yx的图象向下平移 4 个单位长度得到 （1）求这个一次函数的解析式； （2）一次函数ykxb的图象与 x轴的交点为 A，函数(0)ymx m的图象与一次函数ykxb的图象的交点为 B，记线段 OA，AB，BO围成的区域（不含边界）为 W，横、纵坐标都是整数的点叫做整点，若区域 W内恰有 2 个整点，直接写出 m的取值范围 【答案】 （1）4yx （2）21m 或102m 【解析】 【分析】 （1）根据平移的规律写出解析式即可； （2）先求出 A 点的坐标，再根据题意，找出符合题意的整数点，进行求解即可 小问 1 详解】 一次函数0ykxb k的图象由函数y
34、x的图象向下平移 4 个单位长度得到， 这个一次函数的解析式4yx； 【小问 2 详解】 当04yx时，4x ， 一次函数的解析式4yx与 x轴的交点为(4,0)， 当1x 时，可知在第四象限内，整点有(1, 1),(1, 2)， 当2x 时，可知在第四象限内，整点有(2, 1)， 当3x 时，可知在第四象限内无整点， 把(1, 1),(2, 1),(1, 2)分别代入(0)ymx m，得1m 或12m 或2m ， 解得1m 或12m 或2m， 区域 W内恰有 2 个整点， 函数(0)ymx m的图象要在(1, 1),(2, 1)之间，或在(1, 1),(1, 2)之间， 21m 或102m
35、【点睛】本题考查了一次函数图象平移的规律（左加右减，上加下减） ，一次函数的图象和性质，熟练掌握知识点并正确理解题意是解题的关键 23. 如图，AB 是O 的直径，C 为 BA延长线上一点，过点 C作O的切线，切点为 D，过点 B 作 BECD于点 E，连接 AD，BD （1）求证：ABDDBE； （2）如果 CAAB，BD4，求 BE 的长 【答案】 （1）证明见解析； （2）463 【解析】 【分析】 （1）如图 1，连接 OD， 由 CD切O于点 A 得ODCD ， 从而得ODBE， 进而得ODBDBE， 另外由ODBABD即可得出结论； （2）解：设 OA=x，则 CA=AB=2x，C
36、O=CA+OA=3x，先证明 CODCBE，得3=4ODCOxBECBx从而有3=4xBE，另外由ABDDBE得ABDBBDBE，即可求得463BE 【小问 1 详解】 证明：如图，连接 OD， CD 切O于点 A， ODCD ， BECD， ODBE， ODBDBE， OD=OB， ODBABD， ABDDBE； 【小问 2 详解】 解：如图， 设 OA=x，则 CA=AB=2x，CO=CA+OA=3x， ODBE， ,CDOECODCBE ， CODCBE， 3=4ODCOxBECBx即3=4xBE， 3=4xBE， AB 是O的直径， 90ADB， BECD， 90EADB， ABDDB
37、E， ABDDBE， ABDBBDBE， BD4， 32444BEBE， 解得463BE 【点睛】本题主要考查了圆的切线、勾股定理、相似三角形的判定及性质以及平行线的判定及性质，熟练掌握相似三角形的判定及性质是解题的关键 24. 跳台滑雪是冬季奥运会比赛项目之一 记运动员在该项目的运动过程中的某个位置与起跳点的水平距离为 x（单位：m） ，竖直高度为 y（单位：m） ，下面记录了甲运动员起跳后的运动过程中的七组数据： x/m 0 10 20 30 40 50 60 y/m 54.0 57.8 57.6 53.4 45.2 33.0 16.8 下面是小明的探究过程，请补充完整： （1）为观察 y
38、 与 x 之间的关系，建立坐标系，以 x为横坐标，y为纵坐标，描出表中数据对应的 7 个点，并用平滑的曲线连接它们： （2）观察发现， （1）中的曲线可以看作是_的一部分（填“抛物线”或“双曲线”） ，结合图象，可推断出水平距离约为_m（结果保留小数点后一位）时，甲运动员起跳后达到最高点； （3）乙运动员在此跳台进行训练，若乙运动员在运动过程中的最高点的竖直高度达到 61m，则乙运动员运动中的最高点比甲运动员运动中的最高点_（填写“高”或“低”）约_m（结果保留小数点后一位） 【答案】 （1）见详解 （2）抛物线；10.1m （3）高；3.2m 【解析】 【分析】 （1）根据题意画图即可； （
39、2）根据图表求解即可； （3）根据图表求解即可； 【小问 1 详解】 解：如图， 【小问 2 详解】 根据所学函数， （1）中的曲线可以看作是抛物线的一部分； 结合图象，图象的最高点在 10m到 20m之间，可推断出水平距离约为 10.1m时，甲运动员起跳后达到最高点； 【小问 3 详解】 61-57 8=3.2m 乙运动员在此跳台进行训练，若乙运动员在运动过程中的最高点的竖直高度达到 61m，则乙运动员运动中的最高点比甲运动员运动中的最高点高约 3.2m 【点睛】本题主要考查了二次函数图象的性质，掌握相关知识是解题的关键 25. 2022年是中国共产主义青年团建团 100周年，某校团委组织七
40、、八年级学生开展主题为“成团百年，勇当先锋”的团史知识学习活动，为了解这两个年级学生团史知识的学习情况，从七、八年级的学生中，各随机抽取了 20名学生进行测试，获得了他们的成绩（百分制，且成绩均为整数） ，并对数据（成绩）进行了整理、描述和分析，下面给出了部分信息 a 该校七年级抽取的学生测试成绩的数据的频数分布直方图如下 （数据分为 5组7580y，8085y，8590 x，9095y，95100y） b该校七年级抽取的学生测试成绩的数据在8590 x这一组的是：85；85；85；86；87；88 c该校七、八年级抽取的学生的测试成绩的数据的平均数、中位数、众数如下： 平均数 中位数 众数
41、七年级 85.2 m 85 八年级 87 89.5 90 根据以上信息，回答下列问题： （1）写出表中 m的值； （2）此次测试成绩 90分及 90 分以上为优秀 记该校七年级抽取的学生中成绩优秀的人数是1x，八年级抽取的学生中成绩优秀的人数为2x，比较1x，2x的大小，并说明理由； 该校七、八年级各有 200 名学生，假设该校七、八年级学生全部参加此次测试，请估计成绩优秀的学生总人数（直接写出结果） 【答案】 （1）85 （2）12xx，理由见解析 成绩优秀的学生总人数为 150人 【解析】 【分析】 （1）根据七年级共抽取了 20 名学生进行测试，第 10，11 名学生的成绩为 85 分，
42、85 分，即可求解； （2）分别根据题意得出1x，2x的值，进行比较即可； 根据成绩为毓秀的人所占的比例乘以总人数即可求解 【小问 1 详解】 七年级共抽取了 20 名学生进行测试，第 10，11名学生的成绩为 85 分，85分， 1(8585)852m， 故答案为：85； 【小问 2 详解】 12xx，理由如下： 由频数分布直方图可得，1325x ， 八年级成绩的中位数为 89.5 分，且他们的成绩均为整数， 八年级抽取的学生中成绩优秀的人数为 10个，即210 x ， 12xx； 51020020050 1001502020人， 所以，成绩优秀的学生总人数为 150 人 【点睛】本题考查了
43、频数分布直方图，中位数，众数等，用样本估计总体，熟练掌握知识点，准确理解题意是解题的关键 26. 在平面直角坐标系 xOy 中，已知抛物线223yxax （1）求该抛物线的对称轴（用含 a的式子表示） （2）11A xy，22B xy，为该抛物线上的两点，若112xa ，21xa，且12yy，求 a 的取值范围 【答案】 （1）xa （2）0a 或23a 【解析】 【分析】 （1）根据抛物线对称轴公式即可求解； （2）根据二次函数性质分三种情况列不等式求即可； 【小问 1 详解】 解：该抛物线的对称轴为：22 1axa 【小问 2 详解】 当21axx时，12yy； 则，1 1 2aa ，即0
44、a 当12xaxa时，12yy； 则，1 21aaaa，即23a 当12xaxa时，12yy； 则，1 21aaaa，即23a 综上，0a 或23a 【点睛】本题主要考查二次函数的图象及性质，掌握二次函数的图象及性质是解题的关键 27. 如图， 在ABC 中， ABAC， BAC120， D是 BC中点， 连接 AD 点 M 在线段 AD 上 （不与点 A，D 重合） ，连接 MB，点 E在 CA的延长线上且 MEMB，连接 EB （1）比较ABM与AEM 的大小，并证明； （2）用等式表示线段 AM，AB，AE 之间的数量关系，并证明 【答案】 （1）ABMAEM ，证明见解析； （2）AB
45、=AM+AE，证明见解析 【解析】 【分析】 （1）连接 CM，由 ABAC， D是 BC中点得 AD 垂直平分线段 CD， ABMMBDACMMCD，从而有 BM=CM=ME，于是得MBDMCD，AEMACM，即可得ABMAEM ； （2）AB=AM+AE，证明见解析，理由如下：如下图 2，在线段 AC 上取一点 G，使得 AG=AM，连接 MG，ABAC， D是 BC中点，BAC120得60BAMCAD，进而证明AMG是等边三角形，得AG=AM=MG，从而证明 BAMEGM，即可证明 AB=AM+AE， 【小问 1 详解】 解： ABMAEM ，理由如下：如下图 1，连接 CM， ABAC
46、， D是 BC中点， AD 垂直平分线段 CD，ABDACD 即 ABMMBDACMMCD， BM=CM， MEMB， BM=CM=ME， MBDMCD，AEMACM， ABMMBDACMMCD， ABMAEM ； 【小问 2 详解】 解： AB=AM+AE，证明见解析，理由如下：如下图 2，在线段 AC 上取一点 G，使得 AG=AM，连接 MG， ABAC， D是 BC中点，BAC120， 60BAMCAD， AG=AM， AMG是等边三角形， AG=AM=MG，60EGM， BAMEGM， 在EMG和EMA中， BAMEGMABMAEMMAMG BAMEGM， ABEG， EG=AE+A
47、G，AG=AM， AB=AM+AE 【点睛】本题主要考查了等腰三角形的性质、线段垂直平分线的判定及性质、等边三角形的判定及性质以及全等三角形的判定及性质，利用旋转思想作出手拉手全等三角形是解题的关键 28. 在平面直角坐标系 xOy 中， O的半径为 1， A 为任意一点， B为O上任意一点， 给出如下定义： 记 A，B 两点间的距离的最小值为 p（规定：点 A在O上时，0p ） ，最大值为 q，那么把2pq的值称为点 A与O的“关联距离”，记作 d（A，O） （1）如图，点 D，E，F的横、纵坐标都是整数 d（D，O）_； 若点 M在线段 EF上，求 d（M，O）的取值范围； （2）若点 N
48、在直线32 3yx上，直接写出 d（N，O）的取值范围； （3） 正方形的边长为 m， 若点 P在该正方形的边上运动时， 满足 d （P， O） 的最小值为 1， 最大值为10，直接写出 m的最小值和最大值 【答案】 （1）2，2d（M，O）3 （2）d（N，O）3 （3）m的最小值为 1，最大值为252- 【解析】 【分析】 （1）因为 D 到O 的最小值 p=1，最大值 q=3，根据关联距离的定义可求；先求 d（E，O）和 d（F，O） ，则 d（M，O）在其之间即可； （2）当过 O的直线 ONAB 时，d（N，O）最小，根据三角形的面积公式可求 ON 的值，而 ON 无最大值，即可求出
49、 d（N，O）的取值范围； （3） 当正方形是O的外切正方形时， m 的最小值是 1， 当如图 3时， m取最大值10， 即211 0m+ =，可求 m的值，从而求得 m的最小值和最大值 【小问 1 详解】 解：D到O的最小值 p=1，最大值 q=3， d（D，O）=1 322 ， 故答案为 2； 当 M 在点 E 处，d（E，O）=2， 当 M在点 F处，d（F，O）=2432 ， 2d（M，O）3 【小问 2 详解】 解：设 ON=d， p=d-r=d-1，q=d+r=d+1， d（N，O）=1122pqddd+-+= ， N 在直线32 3yx上， 设直线交 x 轴于 B，交 y轴于 A，如图， 则 x=0时，y=2 3，y=0 时，x=-2， A(0,2 3) ，B( 2,0) ， OA=2 3 ，OB=2， AB=224OAOB ， 当 ONAB时，d（N，O）最小， 1122AOBSOA OBAB ON= ， ON=3 ， ON无最大值， d（N，O）3 【小问 3 详解】 解：如图 2，当正方形是O 的外切正方形时，m的最小值是 1， 如图 3，d（P，O）有最大值10 ， 则2110m+ =， 252m =- m 的最小值为 1，最大值为252- 【点睛】本题是新定义题，考查了对新定义的理解，点到直线的距离，勾股定理，解题的关键是准确理解关联距离这个新定义
