1、2022年河南省南阳市唐河县中考一模数学试卷一、选择题（每小题3分，满分30分）1. 绝对值是（ ）A. B. C. D. 2. 2022年3月5日李克强总理在十三届全国人大第五次会议上作政府工作报告时指出，我国经济保持恢复发展，国内生产总值达到114万亿元，增长8.1%，将数据114万亿用科学记数法表示为（ ）A. B. C. D. 3. 下列计算正确的是（ ）A. B. C. D. 4. 如图是由10个同样大小的小正方体摆成的几何体将小正方体移走后，则关于新几何体的三视图描述正确的是（）A. 俯视图不变，左视图不变B. 主视图改变，左视图改变C. 俯视图不变，主视图不变D. 主视图改变，俯
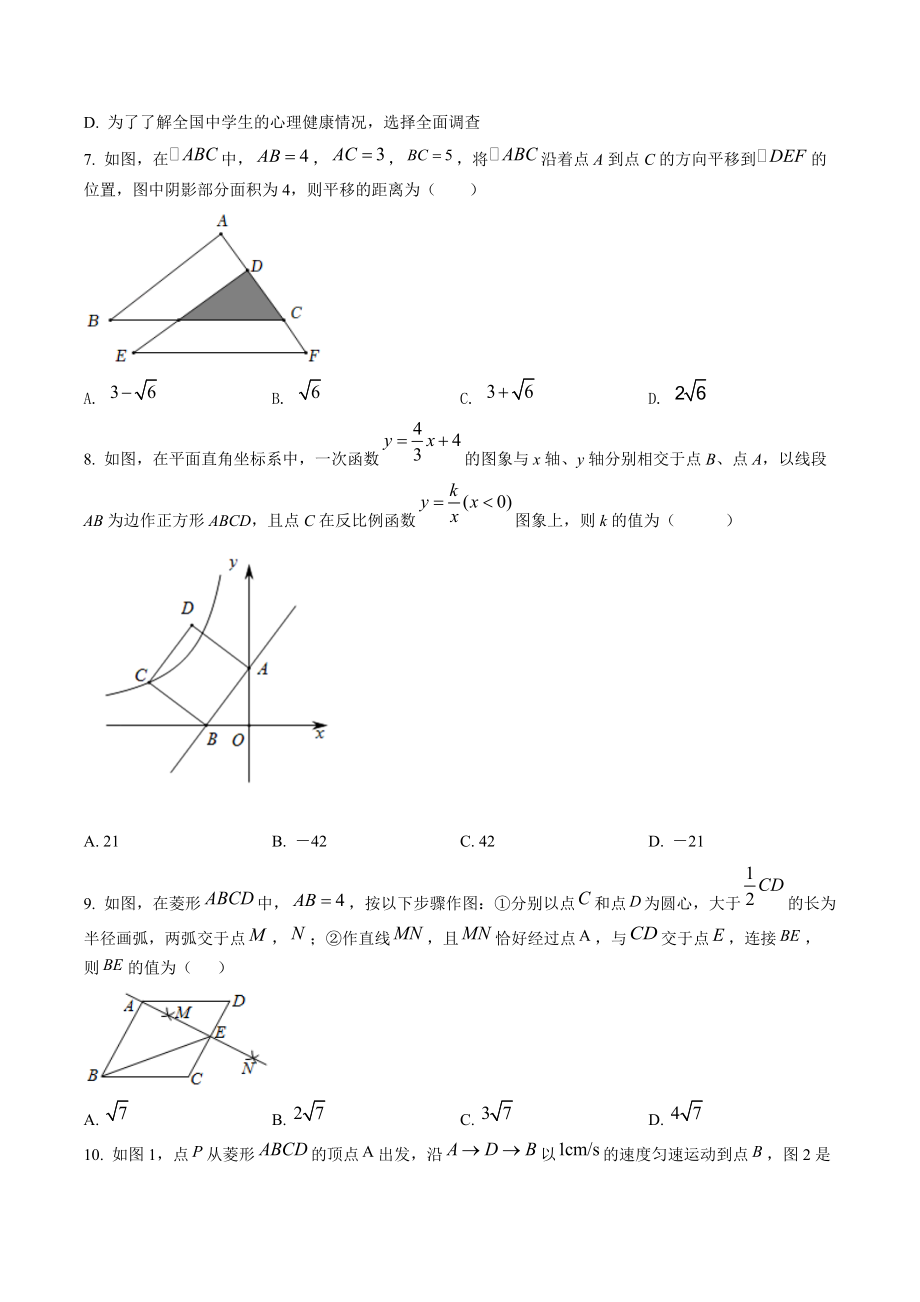
2、视图改变5. 如图，已知直线AD、BE、CF相交于点O，OGAD，且BOC=35，FOG=30，则DOE的度数为（）A. B. C. D. 6. 下列说法正确是（ ）A. “若a是实数，则”是必然事件B. 在一组数据5，7，6，8，6，6，4中，众数和中位数都是6C. 若甲组数据的方差，乙组数据的方差，则乙组数据比甲组数据稳定D. 为了了解全国中学生的心理健康情况，选择全面调查7. 如图，在中，将沿着点A到点C的方向平移到的位置，图中阴影部分面积为4，则平移的距离为（ ）A. B. C. D. 8. 如图，在平面直角坐标系中，一次函数的图象与x轴、y轴分别相交于点B、点A，以线段AB为边作正方
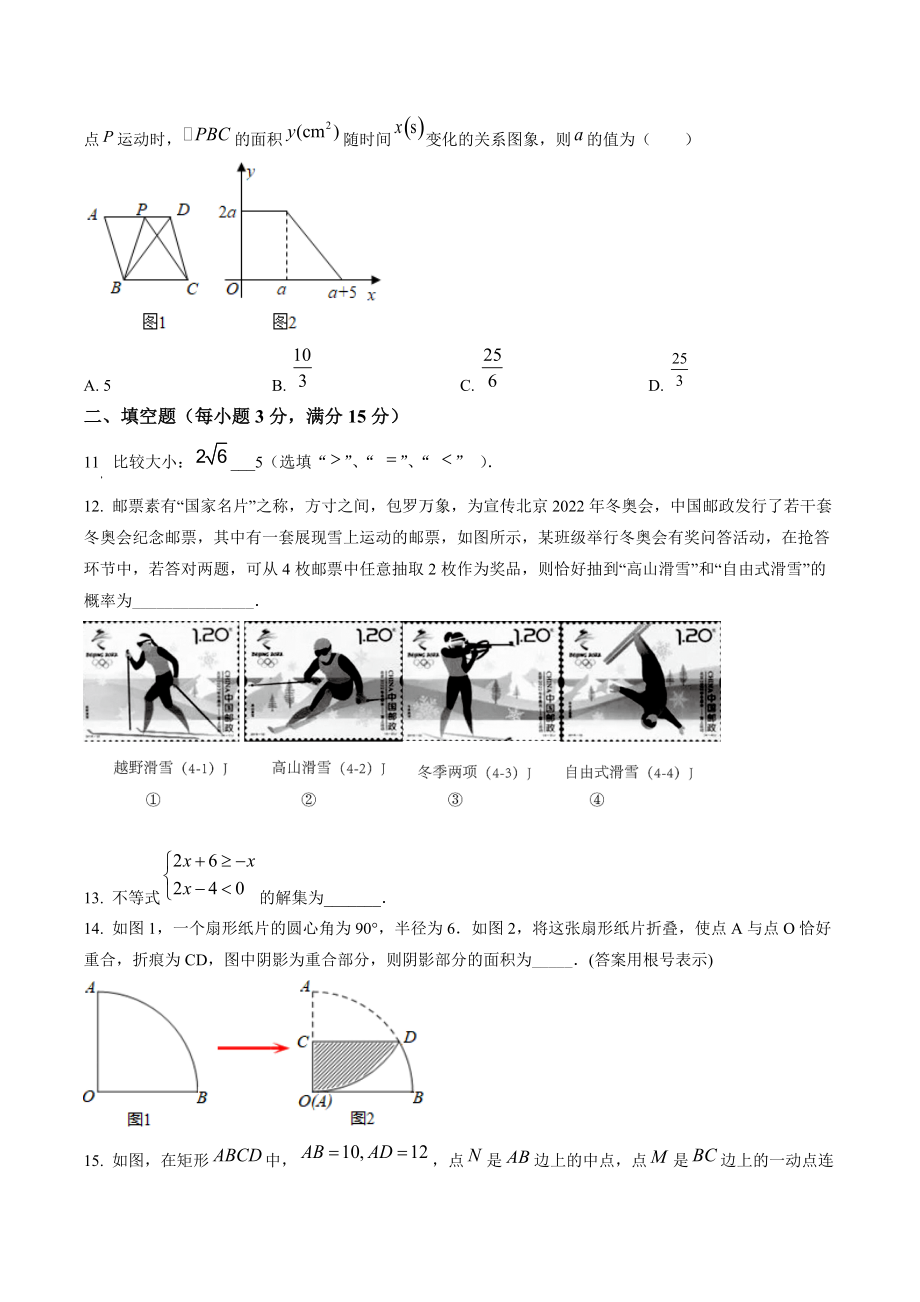
3、形ABCD，且点C在反比例函数图象上，则k的值为（ ）A. 21B. 42C. 42D. 219. 如图，在菱形中，按以下步骤作图：分别以点和点为圆心，大于的长为半径画弧，两弧交于点，；作直线，且恰好经过点，与交于点，连接，则的值为（ ）A. B. C. D. 10. 如图1，点从菱形的顶点出发，沿以的速度匀速运动到点，图2是点运动时，的面积随时间变化的关系图象，则的值为（ ）A. 5B. C. D. 二、填空题（每小题3分，满分15分）11 比较大小：_5（选填“”、“ ”、“ ” ）12. 邮票素有“国家名片”之称，方寸之间，包罗万象，为宣传北京2022年冬奥会，中国邮政发行了若干套冬奥会
4、纪念邮票，其中有一套展现雪上运动的邮票，如图所示，某班级举行冬奥会有奖问答活动，在抢答环节中，若答对两题，可从4枚邮票中任意抽取2枚作为奖品，则恰好抽到“高山滑雪”和“自由式滑雪”的概率为_13. 不等式的解集为_14. 如图1，一个扇形纸片的圆心角为90，半径为6如图2，将这张扇形纸片折叠，使点A与点O恰好重合，折痕为CD，图中阴影为重合部分，则阴影部分的面积为_(答案用根号表示)15. 如图，在矩形中，点是边上的中点，点是边上的一动点连接，将沿折叠，若点的对应点，连接，当为直角三角形时的长为_三、解答题（共8小题，满分75分）16. 先化简：，并从中选取合适的整数代入求值17. 为了纪念中
5、国共产党建党百年，某校进行了“四史”学习教育知识竞赛，该校全体同学参加了知识竞赛收集数据：现随机抽取了部分同学的“四史知识竞赛”成绩，分数如下（单位：分）：85 95 88 68 88 86 95 93 87 93 98 99 88 100 97 80 85 92 94 84 80 78 90 98 85 96 98 86 93 80 86 100 82 78 98 88 100 76 88 99整理分析数据：成绩（单位：分）频数（人数）117（1）填空；，；（2）补充完整频数分布直方图，并求出成绩优秀（80分及以上）的学生占全校学生人数的百分比；（3）学校决定表彰“四史知识竞赛”成绩在100
6、分的同学根据上面统计结果估计该校3000人中，约有多少人将获得表彰；（4）通过“四史知识竞赛”以及学习党史的过程中，写出你最深的感悟18. 如图，AB与O相切于点C，且C为线段AB的中点，直线AO与O交于点E和点D，OB与O交于点F，连接DF，DC（1）求证：CDFCDE；（2）若DE10，DF8，则CD；连接CO，CF，当B的度数为时，四边形ODFC是菱形19. 2021年“五一”期间，修复后的安阳老城东南城墙及魁星阁与市民见面，这一始建于北魏天兴元年（公元398年）的建筑，在1600多年后，以崭新的面貌向世人展示历史印记，古代安阳“魁星取水”景观即将重现某数学学习小组利用卷尺和自制的测角仪
7、测量魁星阁顶端距离地面的高度，如图所示，他们在地面一条水平步道上架设测角仪，先在点处测得魁星阁顶端的仰角是26，朝魁星阁方向走20米到达处，在处测得魁星阁顶端的仰角是45若测角仪和的高度均为米，求魁星阁顶端距离地面的高度（图中的值）（参考数据：，结果精确到米）20. 如图，一次函数的图象与反比例函数的图象交于二、四象限内的、两点，点的坐标为，点的坐标为（1）则，；（2）若时，则的取值范围是；（3）过点作轴于点，连接，过点作于点，求线段的长21. 冰墩墩（Bing Dwen Dwen），是2022年北京冬季奥运会的吉祥物将熊猫形象与富有超能量的冰晶外壳相结合，头部外壳造型取自冰雪运动头盔，装饰彩
8、色光环，整体形象酷似航天员冬奥会来临之际，冰墩墩玩偶非常畅销小冬在某网店选中A，B两款冰墩墩玩偶，决定从该网店进货并销售两款玩偶的进货价和销售价如表：价格类别A款玩偶B款玩偶进货价（元/个）2015销售价（元/个）2820（1）第一次小冬550元购进了A，B两款玩偶共30个，求两款玩偶各购进多少个（2）第二次小冬进货时，网店规定A款玩偶进货数量不得超过B款玩偶进货数量一半小冬计划购进两款玩偶共30个，应如何设计进货方案才能获得最大利润，最大利润是多少？（3）小冬第二次进货时采取了（2）中设计方案，并且两次购进的玩偶全部售出，请从利润率的角度分析，对于小冬来说哪一次更合算？（注：利润率=（利润成
9、本）100%）22. 如图，已知抛物线yx2+bx+c与一直线相交于A（1，0），C（2，3）两点，与y轴交于点N，其项点为D（1）填空：抛物线的解析式为 ；（2）若P是抛物线上位于直线AC上方的一个动点，设点P的横坐标为t，过点P作y轴的平行线交AC与M，当t为何值时，线段PM的长最大，并求其最大值；（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EFBD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，请直接写出点E的坐标；若不能，请说明理由23. （1）（问题发现）如图1，ABC和ADE均为等边三角形，点B，D，E在同一条直线上填空：线段
10、BD，CE之间的数量关系为 ；BEC = （2）（类比探究）如图2，ABC和ADE均为等腰直角三角形，ACB=AED=90，AC=BC，AE=DE，点B，D，E在同一条直线上，请判断线段BD，CE之间的数量关系及BEC的度数，并给出证明（3）如图3，在ABC中，ACB=90，A=30，AB = 5，点D在AB 边上，DEAC于点E，AE = 3，将ADE绕点A旋转，当DE所在直线经过点B时，CE的长是多少？（直接写出答案）2022年河南省南阳市唐河县中考一模数学试卷一、选择题（每小题3分，满分30分）1. 的绝对值是（ ）A. B. C. D. 【答案】B【解析】【分析】根据负数的绝对值是它的
11、相反数，即可解答【详解】解：的绝对值是故选B【点睛】本题主要考查绝对值，熟练掌握求一个数的绝对值是解题的关键2. 2022年3月5日李克强总理在十三届全国人大第五次会议上作政府工作报告时指出，我国经济保持恢复发展，国内生产总值达到114万亿元，增长8.1%，将数据114万亿用科学记数法表示为（ ）A. B. C. D. 【答案】C【解析】【分析】用科学记数法表示较大数时，一般形式为a10n，其中1|a|10，n为整数，且n比原来的整数位数少1，据此判断即可【详解】解：114万亿1140000000000001.141014故选：C【点睛】此题主要考查了用科学记数法表示较大的数，一般形式为a10
12、n，其中1|a|10，确定a与n的值是解题的关键3. 下列计算正确的是（ ）A. B. C. D. 【答案】D【解析】【分析】利用同合并同类项的法则，幂的乘方的法则，同底数幂的除法的法则，同底数幂的乘法的法则，对各项进行运算即可【详解】解：A.不是同类项，不能合并，不符合题意；B.，计算错误，不符合题意；C.，计算错误，不符合题意；D.，计算正确，符合题意；故选D【点睛】本题主要考查同底数幂的除法，合并同类项，幂的乘方，同底数幂的乘法，解答的关键是对相应的运算法则的掌握4. 如图是由10个同样大小的小正方体摆成的几何体将小正方体移走后，则关于新几何体的三视图描述正确的是（）A. 俯视图不变，左
13、视图不变B. 主视图改变，左视图改变C. 俯视图不变，主视图不变D. 主视图改变，俯视图改变【答案】A【解析】【分析】结合几何体的形状，结合三视图可得出俯视图和左视图没有发生变化.【详解】将正方体移走后，新几何体的三视图与原几何体的三视图相比，俯视图和左视图没有发生改变，主视图发生了改变，故选A【点睛】本题考查了简单组合体的三视图，根据题意正确掌握三视图的观察角度是解题关键5. 如图，已知直线AD、BE、CF相交于点O，OGAD，且BOC=35，FOG=30，则DOE的度数为（）A. B. C. D. 【答案】D【解析】【分析】根据对顶角相等，以及垂直定义求出所求角度数即可【详解】解：BOC=
14、35，FOG=30，EOF=BOC=35，GOE=GOF+FOE=65，OGAD，GOD=90，DOE=25，故选D【点睛】此题考查了垂线，以及对顶角，熟练掌握各自的性质是解本题的关键6. 下列说法正确的是（ ）A. “若a是实数，则”是必然事件B. 在一组数据5，7，6，8，6，6，4中，众数和中位数都是6C. 若甲组数据的方差，乙组数据的方差，则乙组数据比甲组数据稳定D. 为了了解全国中学生的心理健康情况，选择全面调查【答案】B【解析】【分析】根据随机事件，众数和中位数，方差的意义，抽样调查及普查，分别判断即可【详解】解：A“若a是实数，则”是随机事件，故选项错误，不符合题意；B在一组数据
15、5，7，6，8，6，6，4中，众数和中位数都是6，故选项正确，符合题意；C若甲组数据的方差，乙组数据的方差，则甲组数据比乙组数据稳定， 故选项错误，不符合题意；D为了了解全国中学生的心理健康情况，选择抽样调查，故选项错误，不符合题意故选：B【点睛】此题主要考查了随机事件，众数和中位数，方差的意义，抽样调查及普查，解答本题的关键是熟练掌握各个知识点7. 如图，在中，将沿着点A到点C的方向平移到的位置，图中阴影部分面积为4，则平移的距离为（ ）A. B. C. D. 【答案】A【解析】【分析】根据勾股定理的逆定理求出ABC是直角三角形，求出ABC的面积，根据平移的性质得出ACDF3，DEF的面积A
16、BC的面积6，再根据面积比等于相似比的平方得出即可【详解】解：AB4，AC3，BC5，AB2+AC2BC2，ABC是直角三角形，A90，将ABC沿着点A到点C的方向平移到DEF的位置，DEF的面积ABC的面积6，DFAC3，图中阴影部分面积为4， ，解得：DC ，即平移的距离是CFACDC3，故选：A【点睛】本题考查了平移的性质，勾股定理的逆定理，三角形的面积和相似三角形的性质等知识点，能求出DEF的面积是解此题的关键8. 如图，在平面直角坐标系中，一次函数的图象与x轴、y轴分别相交于点B、点A，以线段AB为边作正方形ABCD，且点C在反比例函数图象上，则k的值为（ ）A. 21B. 42C.
17、 42D. 21【答案】D【解析】【分析】过点C作 轴，垂足为E，证明 ，可得点C坐标，代入求解即可【详解】如图，过点C作 轴，垂足为E 一次函数的图象与x轴、y轴分别相交于点B、点A 当 时， A（0，4）B（-3，0） 四边形ABCD是正方形ABCD 在 和中 C（-7，3）点C在反比例函数图象上 故选：D【点睛】本题考查了一次函数图象与坐标轴的交点、正方形的性质、求反比例函数的系数即全等三角形的判定和性质，正确的做出辅助线以及运用数形结合的思想是解题的关键9. 如图，在菱形中，按以下步骤作图：分别以点和点为圆心，大于的长为半径画弧，两弧交于点，；作直线，且恰好经过点，与交于点，连接，则的
18、值为（ ）A. B. C. D. 【答案】B【解析】【分析】由作图可知AE垂直平分CD，则AED=90，DE=CE，在RtAED中，可得DAE=30，由勾股定理得AE=，由菱形的性质可求得BAE=90，在RtABE中，根据勾股定理即可求出BE的长【详解】解：由作图可知AE垂直平分CD，AED=90，DE=CE，四边形ABCD是菱形，CD=AD=AB=4，DE=CD=2，在RtAED中，DE=AD，DAE=30，AE=，D=60，BAD=120，BAE=BAD-DAE=90，在RtABE中，BE=故选B【点睛】本题考查了线段垂直平分线的性质，菱形的性质，直角三角形的性质和勾股定理，根据菱形的性质
19、和线段垂直平分线的性质证得BAE=90是解决此题的关键10. 如图1，点从菱形的顶点出发，沿以的速度匀速运动到点，图2是点运动时，的面积随时间变化的关系图象，则的值为（ ）A. 5B. C. D. 【答案】C【解析】【分析】过点作，根据图象的三角形的面积可得菱形的边长为5，再利用菱形的性质和勾股定理列方程可求【详解】解：过点作，菱形中，当点在边上运动时，的值不变，即菱形的边长是，即当点在上运动时，逐渐减小，在中，解得故选：C【点睛】本题主要考查菱形的性质和勾股定理，掌握菱形的性质及勾股定理是关键二、填空题（每小题3分，满分15分）11. 比较大小：_5（选填“”、“ ”、“ ” ）【答案】【解
20、析】【分析】先把两数值化成带根号的形式，再根据实数的大小比较方法即可求解【详解】解：，而2425，5故答案：【点睛】此题主要考查了实数的大小的比较，当一个带根号的无理数和一个有理数进行比较时，首选的方法就是把它们还原成带根号的形式，然后比较被开方数即可解决问题12. 邮票素有“国家名片”之称，方寸之间，包罗万象，为宣传北京2022年冬奥会，中国邮政发行了若干套冬奥会纪念邮票，其中有一套展现雪上运动的邮票，如图所示，某班级举行冬奥会有奖问答活动，在抢答环节中，若答对两题，可从4枚邮票中任意抽取2枚作为奖品，则恰好抽到“高山滑雪”和“自由式滑雪”的概率为_【答案】【解析】【分析】画树状图，共有12
21、种等可能结果，其中恰好抽到“高山滑雪”和“自由式滑雪”的有2种结果，再由概率公式求解即可【详解】“越野滑雪”、“高山滑雪”、“冬季两项”、“自由式滑雪”分别记为甲、乙、丙、丁，画树状图如下：共有12种等可能结果，其中恰好抽到乙和丁即“高山滑雪”和“自由式滑雪”的有2种结果，恰好抽到“高山滑雪”和“自由式滑雪”的概率为：【点睛】此题考查的是用树状图法求概率树状图法可以不重复不遗漏的列出所有可能的结果，适合两步或两步以上完成的事件用到的知识点为：概率所求情况数与总情况数之比13. 不等式的解集为_【答案】【解析】【分析】分别求出不等式组中两不等式的解集，找出两解集的公共部分即可【详解】解：，由得：
22、x2，由得：x2，则不等式组的解集为2x2故答案为：2x2【点睛】此题考查了解一元一次不等式组，熟练掌握不等式组取解集的方法是解本题的关键14. 如图1，一个扇形纸片的圆心角为90，半径为6如图2，将这张扇形纸片折叠，使点A与点O恰好重合，折痕为CD，图中阴影为重合部分，则阴影部分的面积为_(答案用根号表示)【答案】6【解析】【分析】连接OD，利用折叠性质得由弧AD、线段AC和CD所围成的图形的面积等于阴影部分的面积，根据勾股定理求出CD=3 ，从而得到CDO=30，COD=60，然后根据扇形面积公式，利用由弧AD、线段AC和CD所围成的图形的面积=S扇形AOD-SCOD，进行计算即可【详解】
23、连接OD，扇形纸片折叠，使点A与点O恰好重合，折痕为CD，ACOC，OD2OC6，CDO30，COD60，由弧AD、线段AC和CD所围成的图形的面积S扇形AODSCOD阴影部分的面积为6，故答案为6【点睛】本题考查是扇形面积的计算折叠的性质，将不规则图形面积转化为规则图形的面积、记住扇形面积的计算公式是解题的关键15. 如图，在矩形中，点是边上的中点，点是边上的一动点连接，将沿折叠，若点的对应点，连接，当为直角三角形时的长为_【答案】5或【解析】【分析】分以下三种情况讨论：当；当；当时，分别根据勾股定理列方程求解即可【详解】当为直角三角形时，当时， N为中点， ，即，点的对应点不能落在所在直线
24、上，故该情况不存在；如图1，当时，由折叠的性质得：，得；如图2，当时，故三点共线，设，则，在中，则，在中，由勾股定理可得，即，解得，即综上所述，满足条件的的值为5或【点睛】本题考查了折叠问题，矩形的性质，以及勾股定理解题时注意：折叠前后两图形全等，即对应线段相等；对应角相等本题有三种可能情况，需要分类讨论，避免漏解三、解答题（共8小题，满分75分）16. 先化简：，并从中选取合适的整数代入求值【答案】；-1（答案不唯一）【解析】【分析】先根据分式的加减乘除的运算法则对分式进行化简，在根据分式有意义的条件进行取值，最后代入求值，即可求解【详解】解：要使原分式有意义，则，又，且为整数，可取，0，1
25、，当时，原式【点睛】本题主要考查了分式的化简求值和分时有意义的条件，熟练掌握分式混合运算的法则是解题的关键17. 为了纪念中国共产党建党百年，某校进行了“四史”学习教育知识竞赛，该校全体同学参加了知识竞赛收集数据：现随机抽取了部分同学的“四史知识竞赛”成绩，分数如下（单位：分）：85 95 88 68 88 86 95 93 87 93 98 99 88 100 97 80 85 92 94 84 80 78 90 98 85 96 98 86 93 80 86 100 82 78 98 88 100 76 88 99整理分析数据：成绩（单位：分）频数（人数）117（1）填空；，；（2）补充完
26、整频数分布直方图，并求出成绩优秀（80分及以上）的学生占全校学生人数的百分比；（3）学校决定表彰“四史知识竞赛”成绩在100分的同学根据上面统计结果估计该校3000人中，约有多少人将获得表彰；（4）通过“四史知识竞赛”以及学习党史的过程中，写出你最深的感悟【答案】（1）3；19 （2）补充完整的频数分布直方图见解析；优秀的学生占全校学生人数的百分比为 （3）该校3000人中获得表彰人数约有225人 （4）通过“四史知识竞赛”以及学习党史的过程中，我们更加热爱祖国，热爱中国共产党【解析】【分析】（1）根据题意所给数据即可得a的值，用总数减去前三组的频数即可得c的值；（2）结合（1）即可补充完整频
27、数分布直方图，进而可得80分及以上的学生占全校学生人数的百分比；（3）利用样本估计总体的方法即可估计该校3000人中，约有多少人将获得表彰；（4）通过以上数据的分析即可写出感悟【小问1详解】解：根据题意可知：，；故答案为：3，19；【小问2详解】补充完整的频数分布直方图如图，优秀的学生占全校学生人数的百分比为：【小问3详解】该校3000人中获得表彰人数约有人；【小问4详解】合适，积极即可如：通过“四史知识竞赛”以及学习党史的过程中，我们更加热爱祖国，热爱中国共产党【点睛】本题考查了频数分布直方图，用样本估计总体，频数分布表，解决本题的关键是准确画出频数分布直方图18. 如图，AB与O相切于点C
28、，且C为线段AB的中点，直线AO与O交于点E和点D，OB与O交于点F，连接DF，DC（1）求证：CDFCDE；（2）若DE10，DF8，则CD；连接CO，CF，当B的度数为时，四边形ODFC是菱形【答案】（1）见解析；（2）；30【解析】【分析】（1）连接OC由切线的性质得OCA90，由C为线段AB的中点得出OC垂直平分线段AB，则OAOB，得AOCBOC，由圆周角定理即可得出结论；（2）连接OC，过点O作ONDF于N，延长DF交AB于M，先求出DNNFDF4，由勾股定理得，易证CDFOCD，得OCDF，则OCMCMN180，求出CMN90，证得四边形OCMN是矩形，得出ONCM3，MNOC5
29、，DM9，由勾股定理即可得出结果；易证OCF是等边三角形，则COB60，由OCB90，即可得出结果【详解】（1）证明：连接OC如图1所示：AB是O的切线，OCA90，C为线段AB的中点，OC垂直平分线段AB，OAOB，AOCBOC，CDFBOC，CDEAOC，CDFCDE；（2）解：连接OC，过点O作ONDF于N，延长DF交AB于M，如图2所示：ONDF，ODOF，DF8，DNNFDF4，DE10，OD5，在RtOND中，由勾股定理得：ON3，OCOD，CDEOCD，CDFCDE，CDFOCD，OCDF，OCM+CMN180，OCM90，CMN90，ONM90，四边形OCMN是矩形，ONCM3
30、，MNOC5，DMDN+MN4+59，在RtCMD中，由勾股定理得：CD3，故答案为：3；如图3所示：四边形ODFC是菱形，OCCF，OCOF，OCF是等边三角形，COB60，OCB90，B30，故答案为：30【点睛】本题是圆综合题，考查了圆周角定理、切线的性质、平行线的判定与性质等知识,熟练掌握圆周角定理、切线的性质和矩形的判定与性质是解题的关键19. 2021年“五一”期间，修复后的安阳老城东南城墙及魁星阁与市民见面，这一始建于北魏天兴元年（公元398年）的建筑，在1600多年后，以崭新的面貌向世人展示历史印记，古代安阳“魁星取水”景观即将重现某数学学习小组利用卷尺和自制的测角仪测量魁星阁
31、顶端距离地面的高度，如图所示，他们在地面一条水平步道上架设测角仪，先在点处测得魁星阁顶端的仰角是26，朝魁星阁方向走20米到达处，在处测得魁星阁顶端的仰角是45若测角仪和的高度均为米，求魁星阁顶端距离地面的高度（图中的值）（参考数据：，结果精确到米）【答案】魁星阁顶端距离地面的高度约为米【解析】【分析】推出四边形CFGD是矩形，于是得到，求得DE=AD，设AE=CE=x，得到BE，解直角三角形即可得到答案【详解】由题意知，四边形是矩形设米在中，在中，即解得（米）答：魁星阁顶端距离地面的高度约为米【点睛】本题考查了解直角三角形应用-仰角俯角问题，要求学生能借助仰角构造直角三角形并解直角三角形20
32、. 如图，一次函数的图象与反比例函数的图象交于二、四象限内的、两点，点的坐标为，点的坐标为（1）则，；（2）若时，则的取值范围是；（3）过点作轴于点，连接，过点作于点，求线段的长【答案】（1）， （2）或 （3）【解析】【分析】（1）先将点坐标代入反比例函数解析式中，求出，再将点坐标代入反比例函数解析式中求出；（2）根据图象直接得出结论；（3）先求出，再求出，最后用三角形的面积公式建立方程求解，即可得出结论【小问1详解】点，在反比例函数的图象上，反比例函数的解析式为，在反比例函数的图象上，故答案为：，；【小问2详解】由（1）知，当或时，故答案为：或；【小问3详解】轴，点到的距离，【点睛】此题是
33、反比例函数综合题，主要考查了待定系数法，两点间的距离公式，三角形的面积公式，用方程的思想解决问题是解本题的关键21. 冰墩墩（Bing Dwen Dwen），是2022年北京冬季奥运会的吉祥物将熊猫形象与富有超能量的冰晶外壳相结合，头部外壳造型取自冰雪运动头盔，装饰彩色光环，整体形象酷似航天员冬奥会来临之际，冰墩墩玩偶非常畅销小冬在某网店选中A，B两款冰墩墩玩偶，决定从该网店进货并销售两款玩偶的进货价和销售价如表：价格类别A款玩偶B款玩偶进货价（元/个）2015销售价（元/个）2820（1）第一次小冬550元购进了A，B两款玩偶共30个，求两款玩偶各购进多少个（2）第二次小冬进货时，网店规定A
34、款玩偶进货数量不得超过B款玩偶进货数量的一半小冬计划购进两款玩偶共30个，应如何设计进货方案才能获得最大利润，最大利润是多少？（3）小冬第二次进货时采取了（2）中设计的方案，并且两次购进的玩偶全部售出，请从利润率的角度分析，对于小冬来说哪一次更合算？（注：利润率=（利润成本）100%）【答案】（1）A款玩偶购进20个，则B款玩偶购进10个 （2）A款玩偶购进10个，则B款玩偶购进20个，才能获得最大利润，最大利润是180元 （3）第二次更合算【解析】【分析】（1）设A款玩偶购进a个，则B款玩偶购进（30-a）个，根据题意，列出方程，即可求解；（2）设获得利润w元，A款玩偶购进x个，则B款玩偶购
35、进（30-x）个，根据题意，列出函数关系式，再根据一次函数的增减性，即可求解；（3）分别求出两次的利润率，即可求解【小问1详解】解：设A款玩偶购进a个，则B款玩偶购进（30-a）个，根据题意得：，解得：，30-a=10，答：A款玩偶购进20个，则B款玩偶购进10个；【小问2详解】解：设获得利润w元，A款玩偶购进x个，则B款玩偶购进（30-x）个，根据题意得：， A款玩偶进货数量不得超过B款玩偶进货数量的一半，解得：，w随x的增大而增大，当时，的值最大，最大值为310+150=180，答：A款玩偶购进10个，则B款玩偶购进20个，才能获得最大利润，最大利润是180元；【小问3详解】解：第一次的利
36、润率为：，第二次的利润率为：，第二次更合算【点睛】本题主要考查了一元一次方程的应用，一次函数的应用，明确题意，准确得到等量关系是解题的关键22. 如图，已知抛物线yx2+bx+c与一直线相交于A（1，0），C（2，3）两点，与y轴交于点N，其项点为D（1）填空：抛物线的解析式为 ；（2）若P是抛物线上位于直线AC上方的一个动点，设点P的横坐标为t，过点P作y轴的平行线交AC与M，当t为何值时，线段PM的长最大，并求其最大值；（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EFBD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，请直接写出点E的
37、坐标；若不能，请说明理由【答案】（1）yx2+2x+3；（2）当t=时，PM有最大值，最大值为；（3）（0，1）或（，）或（，）【解析】【分析】（1）运用待定系数法即可解决；（2）依题意得P（t，t2+2t+3），表示M点坐标，再求出PM长的函数表达式，依据二次函数性质求最值；（3）运用配方法求顶点D坐标，由以B，D，E，F为顶点的四边形能为平行四边形，且EFBD，可得EFBD，设点E（m，m+1），则F（m，m2+2m+3），EF，建立方程求解即可求得符合题意的点E坐标【详解】解：（1）把A（1，0），C（2，3）代入yx2+bx+c得，解得，抛物线的解析式为：yx2+2x+3；故答案为：y
38、x2+2x+3；（2）设直线AC的解析式为y=mx+n，把A（1，0），C（2，3）代入得，解得，直线AC的解析式为y=x+1，依题意得，P（t，t2+2t+3），M(t,t+1),PM=t2+2t+3-(t+1)= t2+t+2=-(t-)2+,当t=时，PM有最大值，最大值为；（3）yx2+2x+3（x1）2+4顶点D（1，4），把x=1代入y=x+1得，y=2，B（1，2），BD2，设点E（m，m+1），则F（m，m2+2m+3），EF，EFBD，当EFBD时，以B，D，E，F为顶点的四边形能为平行四边形2，当时，解得：m10，m21（舍去），当时，解得m3，m4；点E的坐标为：（0，1
39、）或（，）或（，）【点睛】本题属于中考压轴题，与二次函数有关的代数几何综合题，涉及知识点多，综合性较强，难度较大，解题时必须熟练掌握并灵活运用相关性质和定理，还要注意数形结合，分类讨论；此题主要考查了二次函数图象和性质，待定系数法求函数解析式，平行四边形性质等23. （1）（问题发现）如图1，ABC和ADE均为等边三角形，点B，D，E在同一条直线上填空：线段BD，CE之间的数量关系为 ；BEC = （2）（类比探究）如图2，ABC和ADE均为等腰直角三角形，ACB=AED=90，AC=BC，AE=DE，点B，D，E在同一条直线上，请判断线段BD，CE之间的数量关系及BEC的度数，并给出证明（3
40、）如图3，在ABC中，ACB=90，A=30，AB = 5，点D在AB 边上，DEAC于点E，AE = 3，将ADE绕点A旋转，当DE所在直线经过点B时，CE的长是多少？（直接写出答案）【答案】（1）BD=CE，60；（2）BD=，BEC=45理由见解析；（3）或【解析】【分析】（1）利用等边三角形的性质和SAS可证明，则有，然后再利用即可求出的度数；（2）首先利用等腰直角三角形的性质和锐角三角函数得出，则有，进而可求出，再根据即可得到；（3）分两种情况进行讨论：将ADE绕点A顺时针旋转，DE所在直线经过点B时和将ADE绕点A逆时针旋转，DE所在直线经过点B时，利用相似三角形的判定及性质求解即可【详解】解：（1）和均为等边三角形， ， 在和中， ， ， ；（2），理由如下：和均为等腰直角三角形，和中，又，；（3）如图，将ADE绕点A逆时针旋转，DE所在直线经过点B时， ， ， ， ， ， ， ， ， ， ， ；如图，将ADE绕点A顺时针旋转，DE所在直线经过点B时，同理可得，综上所述，CE的长度为或【点睛】本题主要考查全等三角形的判定及性质和相似三角形的判定及性质，掌握全等三角形的判定及性质和相似三角形的判定及性质是解题的关键
