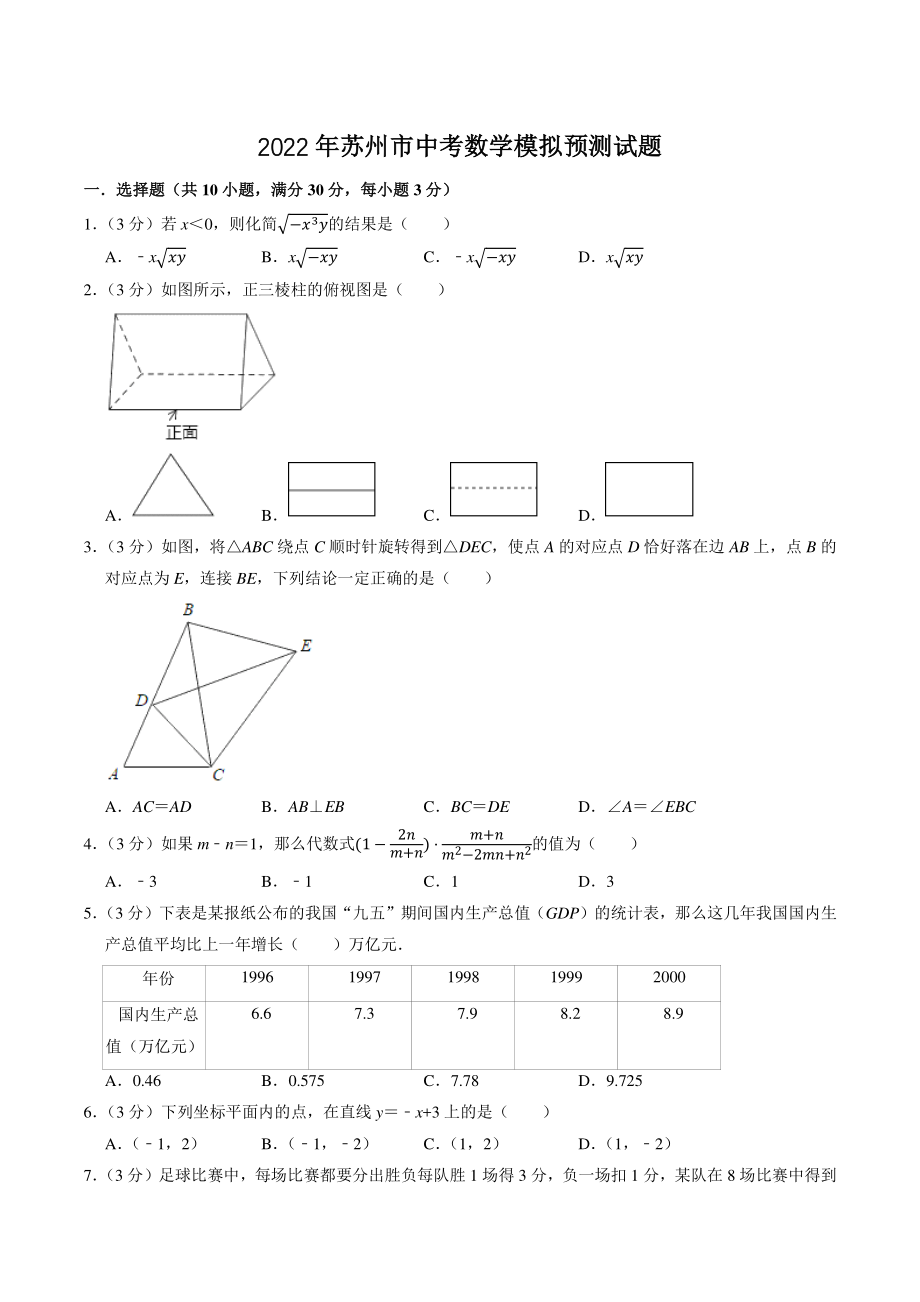
1、20222022 年苏州市中考数学模拟年苏州市中考数学模拟预测试题预测试题 一选择题（共一选择题（共 10 小题，满分小题，满分 30 分，每小题分，每小题 3 分）分） 1 （3 分）若 x0，则化简3的结果是（ ） Ax Bx Cx Dx 2 （3 分）如图所示，正三棱柱的俯视图是（ ） A B C D 3 （3 分）如图，将ABC 绕点 C 顺时针旋转得到DEC，使点 A 的对应点 D 恰好落在边 AB 上，点 B 的对应点为 E，连接 BE，下列结论一定正确的是（ ） AACAD BABEB CBCDE DAEBC 4 （3 分）如果 mn1，那么代数式(1 2+) +22+2的值为（
2、 ） A3 B1 C1 D3 5 （3 分）下表是某报纸公布的我国“九五”期间国内生产总值（GDP）的统计表，那么这几年我国国内生产总值平均比上一年增长（ ）万亿元 年份 1996 1997 1998 1999 2000 国内生产总值（万亿元） 6.6 7.3 7.9 8.2 8.9 A0.46 B0.575 C7.78 D9.725 6 （3 分）下列坐标平面内的点，在直线 yx+3 上的是（ ） A （1，2） B （1，2） C （1，2） D （1，2） 7 （3 分）足球比赛中，每场比赛都要分出胜负每队胜 1 场得 3 分，负一场扣 1 分，某队在 8 场比赛中得到12 分，若设该队
3、胜的场数为 x 负的场数为 y，则可列方程组为（ ） A + = 83 = 12 B = 83 = 12 C + = 183 + = 12 D = 83 + = 12 8 （3 分）如图，抛物线 y1=12( 3)2+1 与 y2a（x+3）21 交于点 A，分别交 y 轴于点 P，Q，过点 A作 x 轴的平行线，分别交两条抛物线于点 B，C已知 B（5，3） ，则以下结论： 两抛物线的顶点关于原点对称； A（2，3） ； C（7，3） ； PQ2 其中正确结论是（ ） A B C D 9 （3 分）如图，在平行四边形 ABCD 中，ABC45，E、F 分别在 CD 和 BC 的延长线上，AE
4、BD，EFC30，AB1则 CF 的长为（ ） A2 + 6 B22 C4 D2 + 3 10 （3 分）如图 1，在ABC 中，ABAC，BCm，D，E 分别是 AB，AC 边的中点，点 P 为 BC 边上的一个动点，连接 PD，PA，PE设 PCx，图 1 中某条线段长为 y，若表示 y 与 x 的函数关系的图象大致如图 2 所示，则这条线可能是（ ） APB BPE CPA DPD 二填空题（共二填空题（共 8 小题，满分小题，满分 24 分，每小题分，每小题 3 分）分） 11 （3 分）健康成年人的心脏全年流过的血液总量为 2540000000 毫升，将 2540000000 用科学
5、记数法表示应为 12 （3 分）分解因式：a3b3 13 （3 分）如图，在正方形纸片上作随机扎针试验，针头扎在阴影区域内的概率为 14 （3 分）如图，在ABA1中，B20，ABA1B，在 A1B 上取一点 C，延长 AA1到 A2，使得 A1A2A1C；在 A2C 上取一点 D，延长 A1A2到 A3，使得 A2A3A2D；，按此做法进行下去，第 n 个等腰三角形的底角的度数为 15 （3 分）若 m2n20，则 m24mn+4n2+5 的值是 16 （3 分）已知 p2x+1，q2x+2，规定 y= 1 + ( )1 + ()，则 y 的最小值是 17 （3 分）已知一个菱形的较短的对角
6、线与较长的对角线的比值为 1：3，则这个菱形中较小的内角为 18 （3 分）在ABC 中，BAC90，BC 的垂直平分线 EF 交 BC 于点 F，交 AB 于点 E，P 是 AC 延长线上一点，连接 FP，将 FP 绕点 F 逆时针旋转 2，得到 FK，连接 CK，如果B（090） ，则;= 三解答题（共三解答题（共 10 小题，满分小题，满分 76 分）分） 19 （5 分）计算： （1） （5）24 + 273； （2）24 2 + 6（8 118） 20 （5 分） （1） = 1 2 + 3 = 3 （2）7 + 3 = 55 + 6 = 8 21 （6 分）先化简，再求值： （:2
7、2;2+84;2）2，其中 a= 3 2 22 （6 分）某教育局为了解本地八年级学生参加社会实践活动情况，随机抽查了八年级学生参加社会实践活动的天数，并用得到的数据绘制了两幅统计图，下面给出了两幅不完整的统计图： 请根据图中提供的信息，回答下列问题： （1）所抽取的八年级学生人数是 ，其中 a ，并写出 8 天所在的扇形所对圆心角的度数为 （2）请补全条形图 （3）如果该市共有八年级学生 2000 人，请你估计“活动时间不少于 7 天”的学生人数大约有多少人？ 23 （8 分）甲和乙玩一个游戏：三张大小、质地都相同的卡片上分别标有数字 2，3，4（背面完全相同） ，现将标有数字的一面朝下，甲
8、从中任意抽取一张，记下数字后放回洗匀，然后乙从中任意抽取一张，计算甲和乙抽得的两个数字之和若和为奇数，则甲胜；若和为偶数，则乙胜 （1）请你用画树状图或列表的方法，求出这两数和为 6 的概率； （2）你认为这个游戏规则对双方公平吗？说明你的理由 24 （8 分）如图，在平面直角坐标系中，四边形 OABC 为矩形，点 C、A 分别在 x 轴和 y 轴的正半轴上，点 D 为 AB 的中点 一次函数 y3x+6 的图象经过点 C、 D， 反比例函数 y=（x0） 的图象经过点 B，求 k 的值 25 （8 分）如图，四边形 ABCD 内接于O，12，延长 BC 到点 E，使得 CEAB，连接 ED
9、（1）求证：BDED （2）若 AB5，BC7，ABC60，求 tanDCB 的值 26 （10 分）如图，在平面直角坐标系中，抛物线 yax2+bx+c 的顶点坐标为 D（1，4） ，与 x 轴的一个交点为 A（3，0） ，与 y 轴的交点为 B （1）求抛物线的解析式； （2）若点 P 是直线 AB 上方抛物线上的一动点，且点 P 到直线 AB 的距离是582，求 P 的坐标； （3） 若点 P 是该抛物线上一动点， 是否存在一点 P， 使PBABAD？若存在， 请写出所有 P 点坐标；若不存在，请说明理由 27 （10 分）父亲告诉小明： “距离地面越远，温度越低” ，并且出示了下面的表
10、格： 距离地面高度（千米） 0 1 2 3 4 5 温度（） 20 14 8 2 4 10 根据上表，父亲还给小明出了下面几个问题，你和小明一起回答： （1）如果用 h（单位：km）表示距离地面的高度，用 T（单位：）表示温度，T 如何随着 h 的变化而变化？写出 T 随着 h 随着 h 变化的函数解析式； （2）画出函数图象； （3）你能预测出距离地面 6km 的高空温度是多少吗？ 28 （10 分）已知在菱形 ABCD 中，AB4，BAD120，点 P 是直线 AB 上任意一点，联结 PC在PCD 内部作射线 CQ 与对角线 BD 交于点 Q（与 B、D 不重合） ，且PCQ30 （1）如
11、图，当点 P 在边 AB 上时，如果 BP3，求线段 PC 的长； （2）当点 P 在射线 BA 上时，设 BPx，CQy，求 y 关于 x 的函数解析式及定义域； （3）联结 PQ，直线 PQ 与直线 BC 交于点 E，如果QCE 与BCP 相似，求线段 BP 的长 参考答案与试题解析参考答案与试题解析 一一选择题（共选择题（共 10 小题，满分小题，满分 30 分，每小题分，每小题 3 分）分） 1 【解答】解：当 x0 时，x0， 3 = ()2 () = x 故选：C 2 【解答】解：俯视图是从上面看所得到的图形，看见的棱用实线表示，看不见的用虚线表示， 故选：B 3 【解答】解：将A
12、BC 绕点 C 顺时针旋转得到DEC， ACCD，BCCE，ABDE，故 A 错误，C 错误； ACDBCE， AADC=1802，CBE=1802， AEBC，故 D 正确； A+ABC 不一定等于 90， ABC+CBE 不一定等于 90，故 B 错误 故选：D 4 【解答】解：(1 2+) +22+2 = (+2+) +()2 =+2+()2 =+()2 =1， 把 mn1 代入上式， 原式1 故选：C 5 【解答】解： （0.7+0.6+0.3+0.7）40.575 故选：B 6 【解答】解：当 x1 时，y（1）+31+34，故选项 A、B 均不符合题意； 当 x1 时，y1+32，
13、故选项 C 符合题意，选项 D 不符合题意； 故选：C 7 【解答】解：设这个队胜 x 场，负 y 场， 根据题意，得 + = 83 = 12 故选：A 8 【解答】解：由抛物线 y1=12( 3)2+1 与 y2a（x+3）21 知，两抛物线的顶点坐标分别是（3，1） ，（3，1） ，则它们关于原点对称，故结论正确 由于 B（5，3） ，且点 A 与点 B 关于直线 x3 对称，所以 A（1，3） ，故结论不正确 由于 A（1，3） ，且点 A 与点 C 关于直线 x3 对称，所以 C（7，3） ，故结论正确 由抛物线 y1=12( 3)2+1=12x23x+112知，P（0，112） ；由
14、 y2a（x+3）21ax2+6ax+9a1 知，Q（0，9a1） 则 PQ=1129a+1=1329a，故结论不正确 故选：B 9 【解答】解：四边形 ABCD 是平行四边形， ABCD，ABDC， AEDB， 四边形 ABDE 是平行四边形， ABDECD， 即 D 为 CE 中点 AB1， CE2， ABCD， ECFABC45， 过 E 作 EHBF 于点 H， CE2，ECF45， EHCH= 2， EFC30， = 3 = 6， = 2 + 6 故选：A 10 【解答】解：选项 A：若 yPB，已知 BCm，观察图形可知 PB 在 xm 取得最小值为 0，故 A 错误； 选项 B：
15、若 yPE，E 是 AC 边的中点，且 ABAC， 可知 PE 在 x=4取得最小值，观察图 2，可知选项 B 错误； 选项 C：若 yPA，由 ABAC，可知 PA 在 x=2取得最小值，故 C 错误； 选项 D：由前三个错误，可知本选项正确，且由题意及图形可知 PD 在 x=34处取得最小值，本选项正确 故选：D 二填空题（共二填空题（共 8 小题，满分小题，满分 24 分，每小题分，每小题 3 分）分） 11 【解答】解：将 2540000000 用科学记数法表示为 2.54109 故答案为：2.54109 12 【解答】解：原式（ab） （a2+ab+b2） ， 故答案为： （ab）
16、（a2+ab+b2） 13 【解答】解：将每个小正方形的边长记为 1， 则图中阴影部分面积=122144，正方形纸片的面积329， 针头扎在阴影区域内的概率为49 故答案为：49 14 【解答】解：在ABA1中，B20，ABA1B， BA1A=1802=180202=80， A1A2A1C，BA1A 是A1A2C 的外角， CA2A1=12=802=40； 同理可得， DA3A220，EA4A310， 第 n 个等腰三角形的底角的度数=8021 故答案为：8021 15 【解答】解：m2n20 m2n2 原式（m2n）2+5 4+5 9 故答案为 9 16 【解答】解：p2x+1，q2x+2，
17、 当 pq 时，2x+12x+2， 解得：x14 x14时，pq；当 x14，pq y= 1 + ( )1 + ()，可化为： y= 1 + 2 + 1 (2 + 2) = 4( 14)1 2 1 2 + 2 = 4 + 2(14)， y4x（x14） ，其函数值随自变量的增大而增大，故其在 x=14时取得最小值，即 y1； y4x+2（x14） ，其函数值随自变量的增大而减小，故 y1 y 的最小值是 1 故答案为：1 17 【解答】解：一个菱形的较短的对角线与较长的对角线的比值为 1：3， 菱形的对角线互相垂直， =13， ABO30， ABC60， 故答案为：60 18 【解答】解：如图
18、， 连接 AF， EF 是 BC 的垂直平分线，BAC90， BFCFAF， BBAF， AFC2B2， AFPKFC， FPCK， 在AFP 与CFK 中， = = = AFPCFK， APCK， CKCPAC， 过 F 作 FDAB 于 D， FDcosEF， F 是 BC 的中点，ABAC， DF 为ABC 的中位线， DFAC，DF=12AC， ;=12=2 故答案为：2 三解答题（共三解答题（共 10 小题，满分小题，满分 76 分）分） 19 【解答】解： （1）原式52+36； （2）原式23 +43 33=1733 20 【解答】解： （1） = 1 2 + 3 = 3， 把代
19、入得：22y+3y3，即 y1， 把 y1 代入得：x0， 则方程组的解为 = 0 = 1； （2）7 + 3 = 55 + 6 = 8， 2得：9x18，即 x2， 把 x2 代入得：y3， 则方程组的解为 = 2 = 3 21 【解答】解：原式:2(;2)8(:2)(;2);2 =(+2)28(+2)(2);2 =(2)2(+2)(2);2 =1+2， 当 a= 3 2 时，原式=33 22 【解答】解： （1）所抽取的八年级学生人数是：24040%600（人） ， a1（40%+20%+25%+5%）190%10%， 8 天所在的扇形所对圆心角的度数为：36010%36； 故答案为：60
20、0，10%，36； （2）8 天的人数有：60010%60（人） ， 补全统计图如下： （3）根据题意得： 2000（25%+10%+5%）800（人） 答：估计“活动时间不少于 7 天”的学生人数大约有 800 人 23 【解答】解： （1）列表如下： 2 3 4 2 2+24 2+35 2+46 3 3+25 3+36 3+47 4 4+26 4+37 4+48 由表可知，总共有 9 种结果，其中和为 6 的有 3 种， 则这两数和为 6 的概率39=13； （2）这个游戏规则对双方不公平 理由：因为 P（和为奇数）=49，P（和为偶数）=59，而4959， 所以这个游戏规则对双方是不公平
21、的 24 【解答】解：在 y3x+6 中，令 y0，则3x+60， 解得 x2， C（2，0） ， B（2，2） ， A（0，2） ， 点 D 为 AB 的中点， 点 D（1，2） ， 点 D 在直线 y3x+6 上， 2= 31+6， k6 25 【解答】 （1）证明：12， = ， ADDC， 四边形 ABCD 内接于O， BAD+BCD180， ECD+BCD180， BADECD， 在ABD 和CED 中， = = = ， ABDCED（SAS） ， BDED； （2）解：过点 D 作 DMBE 于 M， AB5，BC7，CEAB5， BEBC+EC12， BDED，DMBE， BMM
22、E=12BE6， CMBCBM1， ABC60，12， 230， DMBMtan2633=23， tanDCB=23 26 【解答】解： （1）抛物线 yax2+bx+c 的顶点坐标为 D（1，4） ， 设抛物线的解析式为：ya（x1）2+4， 抛物线经过点 A（3，0） ， 0a（31）2+4，解得，a1， 抛物线的解析式为：yx2+2x+3； （2）如图 1，连接 PA，过点 P 作 PCx 轴，交 AB 于点 C， A（3，0） ，B（0，3） ， 直线 AB 的解析式为：yx+3，且 = 32， 设点 P（m，m2+2m+3） ，则点 C（m，m+3） ， PC（m2+2m+3）（m+
23、3）m2+3m， =12 ( ) =12(2+ 3)(3 0) =32(2+ 3)， 设 d 为点 P 到直线 AB 距离是582， 又=12 =12 32 582 =158， 32(2+ 3) =158，解得1=12，2=52， 点 P 的坐标为(12，154)或(52，74)； （3）存在，理由： 当点 P 在 x 轴上方时， 如图 2，延长 AD 交 y 轴于点 M，过点 M 作 MGAB 交于点 G，过点 A 作 AHBP 于 y 轴于点 H，则BADBAH， 由点 A、B、D 的坐标知，OBOA3，OBAOAB45， 由点 A、D 的坐标得，直线 AD 的表达式为 y2x+6，则点
24、M（0，6） ， 则 BM633，AM35， 在AGM 中，GBMOBA45，则 BGMG=22MB=322， 则 tanBAD=32232+322=13， PBABAD，BADBAH， PBABAHBAD， tanBAH=13， 在BAH 中，HBA45，tanBAH=13，AB32， 过点 H 作 HRAB 于点 R，设 RHxBR，则 AR3x， 则 AB32 =AR+BR4x，解得 x=324， 则 BH= 2x=32，故点 H 的坐标为（0，32） ， 由点 A、H 的坐标得：直线 AH 的表达式为 y= 12x+32， AHBP， 故设直线 BP 的表达式为 y= 12x+t， 将
25、点 B 的坐标代入上式得：3t，解得 t3， 故直线 BP 的表达式为 y= 12x+3， 联立并解得 =52 =74（不合题意的值已舍去） ， 故点 P 的坐标为（52，74） ； 当点 P（P）在 x 轴下方时， 则 PBAD，同理可得，直线 BP的表达式为 y2x+6， 联立并解得 = 4 = 5（不合题意的值已舍去） ， 故点 P 的坐标为（52，74）或（4，5） 27 【解答】解： （1）根据表中数据的变化规律，T 随着 h 的增大而减小， 设 Tkh+b，把（0，20） ， （1，14）代入得： = 20 + = 14， 解得： = 6 = 20， T6h+20 （2）如图，根据
26、点（0，20） ， （103，0）画出图象 （3）当 h6 时，T66+2016 距离地面 6km 的高空温度是16 28 【解答】解： （1）如图 1 中，作 PHBC 于 H 四边形 ABCD 是菱形， ABBC4，ADBC， A+ABC180， A120， PBH60， PB3，PHB90， BHPBcos60=32，PHPBsin60=332， CHBCBH432=52， PC= 2+ 2=(332)2+ (52)2= 13 （2）如图 1 中，作 PHBC 于 H，连接 PQ，设 PC 交 BD 于 O 四边形 ABCD 是菱形， ABDCBD30， PCQ30， PBOQCO， P
27、OBQOC， POBQOC， =， =， POQBOC， POQBOC， OPQOBC30PCQ， PQCQy， PC= 3y， 在 RtPHB 中，BH=12x，PH=32x， PC2PH2+CH2， 3y2（32x）2+（412x）2， y=3212+483（0 x8） （3）如图 2 中，若直线 QP 交直线 BC 于 B 点左侧于 E 此时CQE120， PBC60， PBC 中，不存在角与CQE 相等， 此时QCE 与BCP 不可能相似 如图 3 中，若直线 QP 交直线 BC 于 C 点右侧于 E 则CQEBQBC+QCP60CBP， PCBE， 只可能BCPQCE75， 作 CFAB 于 F，则 BF2，CF23，PCF45， PFCF23， 此时 PB2+23， 如图 4 中，当点 P 在 AB 的延长线上时， QCE 与BCP 相似， CQECBP120， QCEPCB15， 作 CFAB 于 F FCB30， FCP45， BF=12BC2，CFPF23， PB23 2 综上所述，满足条件的 PB 的值为 2+23或 23 2
