1、2021 年浙江省杭州市滨江区七年级年浙江省杭州市滨江区七年级下期末数学试卷下期末数学试卷 一、选择题：本大题有一、选择题：本大题有 10 个小题，每小题个小题，每小题 3 分，共分，共 30分分 1. 下列是二元一次方程的是（ ） A. 122xx B. 431xy C. 20 xy D. 22xyx 2. 要使分式12xx有意义，则x的取值应满足（ ） A 2x B. 1x C. 2x D. 1x 3. 下列计算正确的是（ ） A. 325aaa B. 3321aa C. 23x xx D. 623aaa 4. 为了解某中学 2500名学生家长对“骑电动车需戴头盔”的态度，从中随机调查 4
2、00 名家长，结果有 380名家长持赞成态度，则下列说法正确的是（ ） A. 调查方式是全面调查 B. 该校只有 380名家长持赞成态度 C. 样本是 400 D. 该校约有 95%的家长持赞成态度 5. 如图，下列说法不正确的是（ ） A. 1和A是同旁内角 B. 2和B是内错角 C. 3和A同位角 D. 4和C是同旁内角 6. 下列计算正确的是（ ） A. 22222xyxyxy B. 22xyxyxy C. 2222xyxxyy D. 222xyxy 7. 下列因式分解正确的是（ ） A. 2999xxx B. 322aaaa aa C. 2212111xxx D. 22228822xx
3、yyxy 8. 某班级第一次用 160元买奖品，第二次又用 600元买奖品，已知第二次买的奖品数量是第一次买的奖品数量的3倍， 但单价比第一次的单价多2元， 设第一次买奖品的单价是x元， 则下列所列方程正确的是 （ ） A. 60016032xx B. 60016032xx C. 60016032xx D. 60016032xx 9. 一个长方体模型的长、 宽、 高分别是 4a （cm） ， 3a （cm） ， a （cm） ， 某种油漆每千克可漆面积为12a（cm） ，则漆这个模型表面需要的油漆是（ ）千克 A. 76a B. 38a C. 276a D. 382a 10. 已知无论 x 取
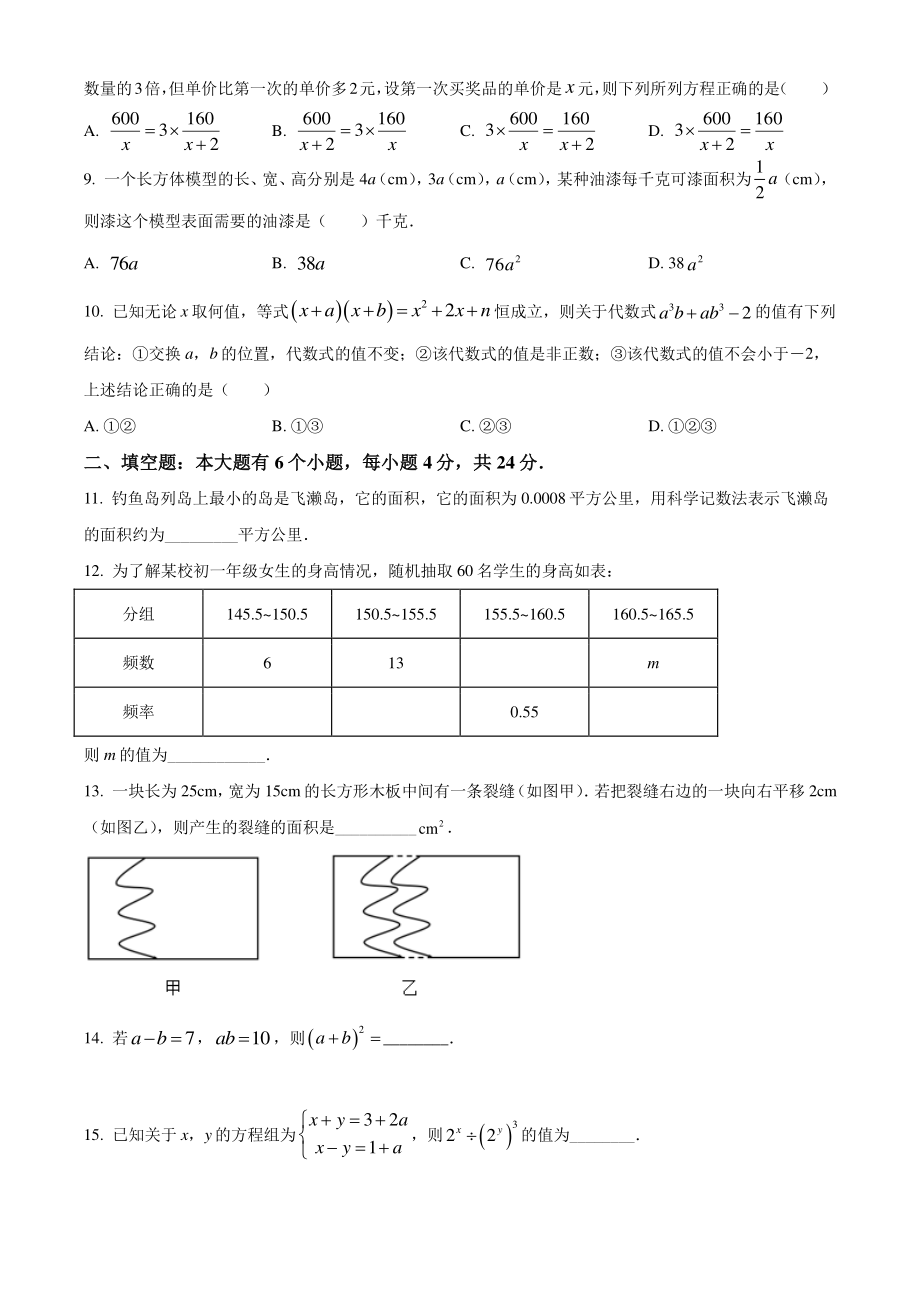
4、何值，等式22xaxbxxn恒成立，则关于代数式332a bab的值有下列结论：交换 a，b的位置，代数式的值不变；该代数式的值是非正数；该代数式的值不会小于2，上述结论正确的是（ ） A. B. C. D. 二、填空题：本大题有二、填空题：本大题有 6 个小题，每小题个小题，每小题 4分，共分，共 24 分分 11. 钓鱼岛列岛上最小的岛是飞濑岛，它的面积，它的面积为 0.0008平方公里，用科学记数法表示飞濑岛的面积约为_平方公里 12. 为了解某校初一年级女生的身高情况，随机抽取 60 名学生的身高如表： 分组 145.5150.5 150.5155.5 155.5160.5 160.5
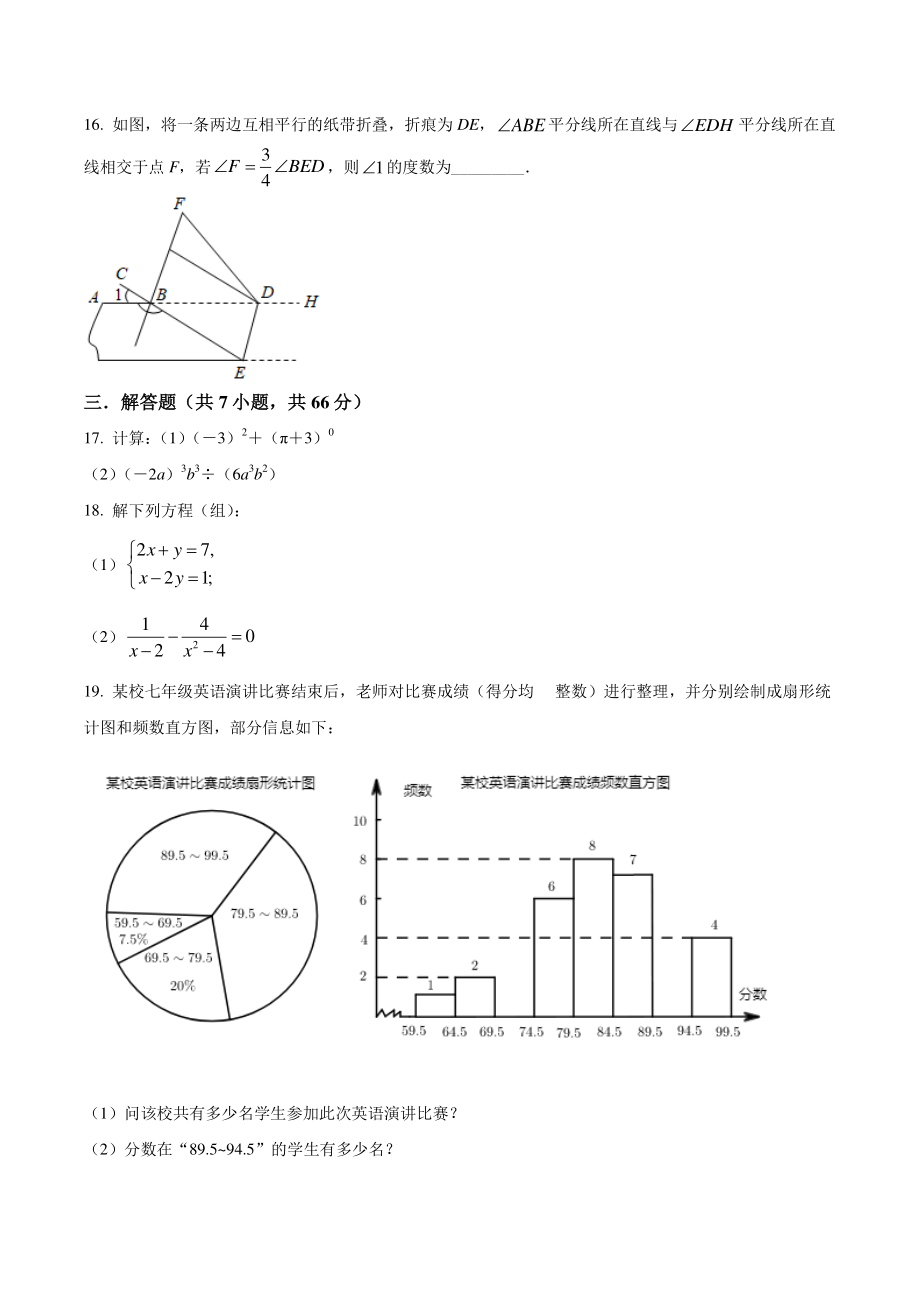
5、165.5 频数 6 13 m 频率 0.55 则 m 的值为_ 13. 一块长为 25cm， 宽为 15cm的长方形木板中间有一条裂缝 （如图甲） 若把裂缝右边的一块向右平移 2cm（如图乙） ，则产生的裂缝的面积是_2cm 14. 若7ab，10ab，则2ab_ 15. 已知关于 x，y的方程组为321xyaxya ，则322xy的值为_ 16. 如图，将一条两边互相平行的纸带折叠，折痕为 DE，ABE平分线所在直线与EDH平分线所在直线相交于点 F，若34FBED，则1的度数为_ 三解答题（共三解答题（共 7 小题，共小题，共 66 分）分） 17. 计算： （1） （3）2（3）0 （
6、2） （2a）3b3（6a3b2） 18. 解下列方程（组） ： （1）27,21;xyxy （2）214024xx 19. 某校七年级英语演讲比赛结束后，老师对比赛成绩（得分均整数）进行整理，并分别绘制成扇形统计图和频数直方图，部分信息如下： （1）问该校共有多少名学生参加此次英语演讲比赛？ （2）分数在“89.594.5”的学生有多少名？ 20. 先化简，再求值： （1） （a2） （a3）3（a1） ，其中 a1 （2）222111442aaaaaa，其中 a2 21. 如图，点 D，F，H，E 都在ABC 的边上，且 DE/ /AC，12180 （1）求证：AE/ /HF； （2）若1
7、3，试猜想BHF 与CFH数量关系，并说明理由 22. 甲地到乙地全程 5.5km，小明从甲地走路去乙地，其中有一段上坡路、一段平路和一段下坡路如果上坡路平均速度为 2km/h，下坡路的平均速度为 5km/h （1）若小明走路从甲地到乙地需74小时，从乙地走路到甲地需1910小时，来回走平路分别都用了14小时，求出小明从甲地到乙地的上坡路和下坡路的路程（请用方程组的方法解） （2）若小明从甲地到乙地，平路上的平均速度为 v（km/h） ，上坡和下坡走的路程分别为 1.5km和 2km若小明从乙地到甲地所用的时间与从甲地到乙地的时间相同，求小明从乙地到甲地平路上走的平均速度（用含 v的代数式表示
8、） 23. 如图，4张长为 x，宽为 y（xy）的长方形纸片拼成一个边长为（xy）的正方形 ABCD （1）用含 x，y 的代数式表示图中所有阴影部分面积的和； （2）当正方形 ABCD的周长是正方形 EFGH周长的三倍时，求xy的值； （3）在（2）的条件下，用题目条件中的 4张长方形纸片，m张正方形 ABCD纸片和 n张正方形 EFHG纸片（m，n 为正整数） ，拼成一个大的正方形（拼接时无空隙、无重叠） ，当 m，n为何值时，拼成的大正方形的边长最小？ 2021 年浙江省杭州市滨江区七年级下期末数学试卷年浙江省杭州市滨江区七年级下期末数学试卷 一、选择题：本大题有一、选择题：本大题有 1
9、0 个小题，每小题个小题，每小题 3 分，共分，共 30分分 1. 下列是二元一次方程的是（ ） A. 122xx B. 431xy C. 20 xy D. 22xyx 【答案】B 【解析】 【分析】根据二元一次方程的定义逐个判断即可 【详解】解：A是一元一次方程，不是二元一次方程，故本选项不符合题意； B是二元一次方程，故本选项符合题意； C是分式方程，不是整式方程，不是二元一次方程，故本选项不符合题意； D是二元二次方程，不是二元一次方程，故本选项不符合题意； 故选：B 【点睛】本题考查了二元一次方程的定义，能熟记二元一次方程的定义是解此题的关键，注意：只含有两个未知数，并且所含未知数的项
10、的最高次数是 1次的整式方程，叫二元一次方程 2. 要使分式12xx有意义，则x的取值应满足（ ） A. 2x B. 1x C. 2x D. 1x 【答案】A 【解析】 【分析】根据分母不等于 0 列式计算即可得解 【详解】解：由题意得，x-20， 解得 x2 故选：A 【点睛】本题考查了分式有意义的条件，分式有意义，分母不等于 0，分式无意义，分母等于 0 3. 下列计算正确的是（ ） A. 325aaa B. 3321aa C. 23x xx D. 623aaa 【答案】C 【解析】 【分析】根据合并同类项、同底数幂的乘法及除法法则进行计算即可 【详解】解：选项 A，a3与 a2不是同类项
11、，不能合并，所以选项 A不符合题意； 选项 B，2a3-a3=a3，所以选项 B不符合题意； 选项 C，根据同底数幂的乘法，xx2=x1+2=x3，所以选项 C符合题意； 选项 D，根据同底数幂的除法，a6 a2=a6-2=a4，所以选项 D 不符合题意 故选：C 【点睛】此题考查了同底数幂的乘法、除法及合并同类项运算，掌握其运算法则是解决此题关键 4. 为了解某中学 2500名学生家长对“骑电动车需戴头盔”的态度，从中随机调查 400 名家长，结果有 380名家长持赞成态度，则下列说法正确的是（ ） A. 调查方式是全面调查 B. 该校只有 380名家长持赞成态度 C. 样本是 400 D.
12、 该校约有 95%的家长持赞成态度 【答案】D 【解析】 【分析】总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目我们在区分总体、个体、样本、样本容量，这四个概念时，首先找出考查的对象从而找出总体、个体再根据被收集数据的这一部分对象找出样本，最后再根据样本确定出样本容量 【详解】解：A调查方式是抽样调查，故此选项不合题意； B400名家长里有 380名家长持赞成态度，故此选项不合题意； C样本容量是 400，故此选项不合题意； D该校约有：380400 100=95%的家长持赞成态度，故此选项符合题意； 故选：D 【点睛
13、】此题考查了总体、个体、样本、样本容量，解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象总体、个体与样本的考查对象是相同的，所不同的是范围的大小样本容量是样本中包含的个体的数目，不能带单位 5. 如图，下列说法不正确的是（ ） A. 1和A是同旁内角 B. 2和B是内错角 C. 3和A是同位角 D. 4和C是同旁内角 【答案】B 【解析】 【分析】根据同旁内角、内错角、同位角的概念判断即可 【详解】解：如图， A1和A是 MN与 AN被 AM 所截成的同旁内角，说法正确，故此选项不符合题意； B2和B不是内错角，说法错误，故此选项符合题意； C3和A是 MN与 AC被 AM 所截成
14、的同位角，说法正确，故此选项不符合题意； D4和C是 MN与 BC被 AC所截成的同旁内角，说法正确，故此选项不符合题意； 故选：B 【点睛】此题考查了同旁内角、内错角、同位角，熟记同旁内角、内错角、同位角概念是解题的关键 6. 下列计算正确的是（ ） A. 22222xyxyxy B. 22xyxyxy C. 2222xyxxyy D. 222xyxy 【答案】C 【解析】 【分析】根据完全平方公式和平方差公式逐个判断即可 【详解】解：A （x+2y） （x-2y）=x2-4y2，故本选项不符合题意； B （x-y） （-x-y）=y2-x2，故本选项不符合题意； C （x-y）2=x2-2
15、xy+y2，故本选项符合题意； D （x+y）2=x2+2xy+y2，故本选项不符合题意； 故选：C 【点睛】本题考查了完全平方公式和平方差公式，能熟记完全平方公式和平方差公式是解此题的关键 7. 下列因式分解正确的是（ ） A. 2999xxx B. 322aaaa aa C. 2212111xxx D. 22228822xxyyxy 【答案】D 【解析】 【分析】A直接利用平方差公式分解因式得出答案；B直接提取公因式 a，进而分解因式即可；C直接利用完全平方公式分解因式得出答案；D首先提取公因式 2，再利用完全平方公式分解因式得出答案 【详解】解：Ax2-9=（x-3） （x+3） ，故此
16、选项不合题意； Ba3-a2+a=a（a2-a+1） ，故此选项不合题意； C （x-1）2-2（x-1）+1=（x-2）2，故此选项不合题意； D2x2-8xy+8y2=2（x-2y）2，故此选项符合题意； 故选：D 【点睛】此题主要考查了提取公因式法以及公式法分解因式，正确运用乘法公式是解题关键 8. 某班级第一次用 160元买奖品，第二次又用 600元买奖品，已知第二次买的奖品数量是第一次买的奖品数量的3倍， 但单价比第一次的单价多2元， 设第一次买奖品的单价是x元， 则下列所列方程正确的是 （ ） A. 60016032xx B. 60016032xx C. 60016032xx D.
17、 60016032xx 【答案】B 【解析】 【分析】设第一次买奖品的单价是 x 元，根据“第二次买的奖品数量是第一次买的奖品数量的 3倍”列出方程即可 【详解】解：设第一次买奖品的单价是 x 元，则第二次的单价为（x+2）元， 根据题意得：60016032xx ， 故选：B 【点睛】考查了由实际问题抽象出分式方程的知识，解题的关键是找到题目中的等量关系并根据等量关系列出方程，难度不大 9. 一个长方体模型的长、 宽、 高分别是 4a （cm） ， 3a （cm） ， a （cm） ， 某种油漆每千克可漆面积为12a（cm） ，则漆这个模型表面需要的油漆是（ ）千克 A. 76a B. 38a
18、 C. 276a D. 382a 【答案】A 【解析】 【分析】先计算出长方体表面积再根据每千克可漆面积为12a（cm2） ，计算油漆的用量即可 【详解】解：由题知，长方体的表面积为： 4a 3a 2+4a a 2+3a a 2=38a2（cm2） ， 需要油漆 38a212a=76a（千克） ， 故选：A 【点睛】本题主要考查长方体的表面积，代数式的计算等知识点，熟练掌握长方体表面积公式是解题的关键 10. 已知无论 x 取何值，等式22xaxbxxn恒成立，则关于代数式332a bab的值有下列结论：交换 a，b的位置，代数式的值不变；该代数式的值是非正数；该代数式的值不会小于2，上述结论
19、正确的是（ ） A. B. C. D. 【答案】A 【解析】 【分析】 由等式 （x+a）（x+b） =x2+2x+n恒成立， 表示出 a+b=2， ab=n， 将 a3b+ab3-2 化简为 ab （a+b）2-2ab-2，将 a+b，ab的值代入然后配方可得 【详解】解：等式（x+a） （x+b）=x2+2x+n恒成立， 即 x2+（a+b）x+ab=x2+2x+n 恒成立， 2ababn， a3b+ab3-2 =ab（a2+b2）-2 =ab（a+b）2-2ab-2 =n22-2n-2 =4n-2n2-2 =-2n2+4n-2 =-2（n-1）20， -2（n-1）2中只与 n有关，故正
20、确； 根据偶次幂为非负数得：-2（n-1）20，故正确，错误； 故选：A 【点睛】本题以恒等式为背景考查了配方法的应用和偶次幂为非负数的应用，关键是根据恒等式求出 a+b，ab 的值，将 a+b，ab 的值代入 a3b+ab3-2 配方化简即可 二、填空题：本大题有二、填空题：本大题有 6 个小题，每小题个小题，每小题 4分，共分，共 24 分分 11. 钓鱼岛列岛上最小的岛是飞濑岛，它的面积，它的面积为 0.0008平方公里，用科学记数法表示飞濑岛的面积约为_平方公里 【答案】8 10-4 【解析】 【分析】用科学记数法表示较小的数，一般形式为 a 10-n，其中 1|a|10，n为由原数左
21、边起第一个不为零的数字前面的 0 的个数所决定 【详解】解：0.0008=8 10-4 故答案为：8 10-4 【点睛】此题考查科学记数法的表示方法，表示时关键要确定 a的值以及 n的值 12. 为了解某校初一年级女生的身高情况，随机抽取 60 名学生的身高如表： 分组 145.5150.5 150.5155.5 155.5160.5 160.5165.5 频数 6 13 m 频率 0.55 则 m 的值为_ 【答案】8 【解析】 【分析】根据频数、频率、总数之间的关系求出身高在“155.5160.5”的频数，进而求出 m 的值 【详解】解：身高在“155.5160.5”的频数为：60 0.5
22、5=33（人） ， m=60-6-13-33=8（人） ， 故答案为：8 【点睛】本题考查频数分布表，理解频数、频率、总数之间的关系是正确计算的前提 13. 一块长为 25cm， 宽为 15cm的长方形木板中间有一条裂缝 （如图甲） 若把裂缝右边的一块向右平移 2cm（如图乙） ，则产生的裂缝的面积是_2cm 【答案】30 【解析】 【分析】利用新长方形的面积减去原长方形的面积得到产生的裂缝的面积 【详解】解：产生的裂缝的面积为： （25+2） 15-25 15 =（27-2） 15 =30（cm2） 故答案为：30 【点睛】 本题主要考查了生活中的平移现象， 利用利用两个长方形形的面积差得出
23、裂缝的面积是解题关键 14. 若7ab，10ab，则2ab_ 【答案】89 【解析】 【分析】先根据完全平方公式得出（a+b）2=（a-b）2+4ab，再代入求出答案即可 【详解】解：a-b=7，ab=10， （a+b）2=（a-b）2+4ab=72+4 10=89， 故答案为：89 【点睛】 本题考查了完全平方公式， 能熟记完全平方公式是解此题的关键， 注意： （a+b）2=a2+2ab+b2， （a-b）2=a2-2ab+b2 15. 已知关于 x，y的方程组为321xyaxya ，则322xy的值为_ 【答案】12 【解析】 【分析】求出关于 x，y的方程组为321xyaxya 的解，将
24、 x、y的值代入 2x （2y）3计算即可 【详解】解：解关于 x，y的方程组为321xyaxya 得， x=2+32a，y=1+12a， 所以 2x （2y）3 =2x 23y =22+1.5a 23+1.5a =2-1 =12， 故答案为：12 【点睛】本题考查解二元一次方程组，同底数幂的除法，幂的乘方，正确的求出二元一次方程组的解，掌握同底数幂的除法法则是正确计算的前提 16. 如图，将一条两边互相平行的纸带折叠，折痕为 DE，ABE平分线所在直线与EDH平分线所在直线相交于点 F，若34FBED，则1的度数为_ 【答案】36 【解析】 【分析】运用平行线的性质、图形翻折的特点，结合FB
25、D 的内角和等于 180 ，从而列出关系式，进而得出结论 【详解】解：如图 令BEDx，则3344FBEDx 由题意得：BEDDEMx ，/ /AHEM BDEDEMx ，180EDHx 1801802EBDBEDBDEx 1802ABEEBDx 又直线BN是ABE的角平分线 12ABNABEx FBDABNx 又直线DF是EDH的角平分线所在直线 1(360)9022xFDEEDH (90)9022xxBDFFDEBDEx 又180BFDFBDFDB 39018042xxx 72x 1180236EBDx ， 故答案为：36 【点睛】本题主要考查平行线的性质、图形翻折的特点，结合三角形内角和
26、的性质，运用化归的思想破解该题 三解答题（共三解答题（共 7 小题，共小题，共 66 分）分） 17 计算： （1） （3）2（3）0 （2） （2a）3b3（6a3b2） 【答案】 （1）10； （2）43b 【解析】 【分析】 （1）直接利用零指数幂的性质化简得出答案； （2）直接利用积的乘方运算法则化简，再利用单项式除单项式运算法则计算得出答案 【详解】解： （1） （-3）2+（+3）0 =9+1 =10； （2） （-2a）3b3 （6a3b2） =-8a3b3 6a3b2 =43b 【点睛】此题主要考查了零指数幂的性质以及积的乘方运算、单项式除单项式运算，正确掌握相关运算法则是解题
27、关键 18. 解下列方程（组） ： （1）27,21;xyxy （2）214024xx 【答案】 （1）31xy； （2）无解 【解析】 【分析】 （1）用加减法解方程组即可； （2）先去分母，再转化为整式方程解答 【详解】解： （1）2721xyxy， 2+得到 5x=15， x=3， 把 x=3代入，得到： y=1， 原方程组的解为31xy； （2）两边都乘以（x-2） （x+2） ，得到： x+2-4=0， x=2， 经检验：x=2不是原方程的解，原方程无解 【点睛】此题主要考查了二元一次方程组的解法和解分式方程，解方程组的关键是消元，消元的方法有两种：加减法消元，代入法消元当系数成倍数
28、关系式一般用加减法消元，系数为 1 时，一般用代入法消元；解分式方程一定要验根 19. 某校七年级英语演讲比赛结束后，老师对比赛成绩（得分均为整数）进行整理，并分别绘制成扇形统计图和频数直方图，部分信息如下： （1）问该校共有多少名学生参加此次英语演讲比赛？ （2）分数在“89.594.5”的学生有多少名？ 【答案】 （1）40 名； （2）10 名 【解析】 【分析】 （1）从两个统计图中可知“59.569.5”的频数为 1+2=3 人，占调查人数的 7.5%，根据频数除以频率等于调查总数可求出结果； （2）求出“69.579.5”的人数，再根据频数分布直方图提供的信息和数据进行计算即可 【
29、详解】解： （1） （1+2） 7.5%=40（名） ， 答：此次参加英语演讲比赛的学生共有 40名； （2）成绩在“69.579.5”组的人数有：40 20%=8（名） ， 成绩在 69.574.5”组的人数为：8-6=2（名） ， 成绩在“89.594.5”组的人数为：40-1-2-2-6-8-7-4=10（名） ， 答：分数在“89.594.5”的有 10 名学生 【点睛】本题考查频数分布直方图、扇形统计图，理解两个统计图中数量之间的关系是正确解答的前提，掌握频率=频数 调查总数是解决问题的关键 20. 先化简，再求值： （1） （a2） （a3）3（a1） ，其中 a1 （2）2221
30、11442aaaaaa，其中 a2 【答案】 （1）a2+4a-9，-4； （2）11a ，13 【解析】 【分析】 （1）整式的混合运算，先算乘法，然后再算加减，最后代入求值； （2）分式的乘除混合运算，将除法转化为乘法，然后从左往右依次进行计算，最后代入求值 【详解】解： （1）原式=a2+3a-2a-6+3a-3 =a2+4a-9， 当 a=1时，原式=1+4-9=-4； （2）原式=2222111aaaaaa =11a ， 当 a=2时，原式=121=13 【点睛】本题考查整式的混合运算和分式的乘除混合运算，掌握运算法则准确计算是解题关键 21. 如图，点 D，F，H，E 都在ABC
31、的边上，且 DE/ /AC，12180 （1）求证：AE/ /HF； （2）若13，试猜想BHF 与CFH的数量关系，并说明理由 【答案】 （1）见解析； （2）BHF=2CFH，理由见解析 【解析】 【分析】 （1）根据平行线的性质得到1=4，再根据12180 可得42180 ，即可证明； （2）根据平行线的性质得到3=C，1=4，可得4=C，再结合平行线的性质可证明5=C，利用三角形外角的性质可得BHF=2CFH 【详解】解： （1）DE/ /AC， 1=4， 12180 ， 42180 ， AE/ /HF； （2）BHF=2CFH，理由是： DE/ /AC， 3=C，1=4， 1=3，
32、4=C， AE/ /FH， 4=5， 5=C， BHF=5+C， BHF=2CFH 【点睛】本题考查了平行线的判定和性质，三角形外角的性质，解题的关键是能根据所学性质定理得到角之间的关系 22. 甲地到乙地全程 5.5km，小明从甲地走路去乙地，其中有一段上坡路、一段平路和一段下坡路如果上坡路的平均速度为 2km/h，下坡路的平均速度为 5km/h （1）若小明走路从甲地到乙地需74小时，从乙地走路到甲地需1910小时，来回走平路分别都用了14小时，求出小明从甲地到乙地的上坡路和下坡路的路程（请用方程组的方法解） （2）若小明从甲地到乙地，平路上的平均速度为 v（km/h） ，上坡和下坡走的路
33、程分别为 1.5km和 2km若小明从乙地到甲地所用的时间与从甲地到乙地的时间相同，求小明从乙地到甲地平路上走的平均速度（用含 v的代数式表示） 【答案】 （1）上坡路路程为 2km，下坡路的路程为 2.5km； （2）40403vvkm/h 【解析】 【分析】 （1）设从甲地到乙地上坡路长 xkm，下坡路长 ykm，然后根据路程，时间，速度之间的等量关系列方程组求解； （2）设从乙地到甲地平路上走的平均速度为 akm/h，然后根据小明从乙地到甲地所用的时间与从甲地到乙地的时间相同列方程求解 【详解】解： （1）设从甲地到乙地上坡路长 xkm，下坡路长 ykm，根据题意可得： 17245411
34、954210 xyxy， 解得：22.5xy， 小明从甲地到乙地的上坡路路程为 2km，下坡路的路程为 2.5km； （2）小明从甲地到乙地，平路上的平均速度为 vkm/h，上坡和下坡走的路程分别为 1.5km和 2km， 从甲地到乙地的平路路程为5.5 1.522km， 设从乙地到甲地平路上走的平均速度为 akm/h，根据题意可得： 1.5221.5222552va， 解得：40403vav 经检验40403vav是原方程的解，且符合题意， 小明从乙地到甲地平路上走平均速度为40403vvkm/h 【点睛】本题考查二元一次方程组和分式方程的应用，找准题目间的等量关系并准确计算是解题关键 23
35、. 如图，4张长为 x，宽为 y（xy）的长方形纸片拼成一个边长为（xy）的正方形 ABCD （1）用含 x，y 的代数式表示图中所有阴影部分面积的和； （2）当正方形 ABCD的周长是正方形 EFGH周长的三倍时，求xy的值； （3）在（2）的条件下，用题目条件中的 4张长方形纸片，m张正方形 ABCD纸片和 n张正方形 EFHG纸片（m，n 为正整数） ，拼成一个大的正方形（拼接时无空隙、无重叠） ，当 m，n为何值时，拼成的大正方形的边长最小？ 【答案】 （1）2xy-y2； （2）2； （3）m=1，n=8 【解析】 【分析】 （1）利用面积差可得阴影部分的面积和； （2）根据正方形
36、ABCD 的周长是正方形 EFGH周长的 3倍列等式可得：x=2y，从而得结论； （3）根据题意可得出大的正方形面积为 4xy+m（x+y）2+n（x-y）2，根据（2）中的结论 x=2y，即大的正方形面积可化为 y2（8+9m+n） ，由题意可知因为大正方形的边长一定是 b的整数倍，则 8+9m+n 是平方数，因为 m、m都是正整数，即 8+9m+n最小是 25，即可得出答案 【详解】解： （1）如图 1， S阴=S正方形ABCD-S正方形EFGH-2SAPB-2SPED =（x+y）2-（x-y）2-212y（x+y）-212xy =2xy-y2 （2）由题意得：4（x+y）=3 4（x-
37、y） ， 解得：x=2y， xy=2； （3）由题意得：拼成一个大的正方形的面积=4xy+m（x+y）2+n（x-y）2， 由（2）知：x=2y， 4xy+m（x+y）2+n（x-y）2=42yy+9my2+ny2=y2（8+9m+n） ， 因为大正方形的边长一定是 y的整数倍， 8+9m+n平方数， m，n都是正整数， 8+9m+n 最小25，即 9m+n=17， m=1，n=8， 此时 4xy+m（x+y）2+n（x-y）2=y2（8+9m+n）=25b2， 则 m=1，n=8时，拼成的大正方形的边长最小 【点睛】本题主要考查了完全平方式和整式的混合运算及列代数式，读懂题意列出代数式是解决本题的关键
