1、2022 年北京中考数学模拟试卷年北京中考数学模拟试卷 一选择题（共一选择题（共 8 小题，满分小题，满分 16 分，每小题分，每小题 2 分）分） 1 （2 分） （2020金坛区二模）若一个几何体的表面展开图如图所示，则这个几何体是（ ） A三棱柱 B四棱柱 C三棱锥 D四棱锥 2 （2 分） （2022宿州一模）电影长津湖2021 年 9 月 30 日上映以来，据有关票房数据显示，截止到 10月 7 日，总票房达 46.49 亿将数据 46.49 亿用科学记数法表示为（ ） A46.49108 B4.649108 C4.649109 D0.46491010 3 （2 分） （2022海淀
2、区校级模拟）如图，点 O 在直线 AB 上，OCOD若BOC60，则AOD 的大小为（ ） A160 B140 C120 D150 4 （2 分） （2021云南）一个十边形的内角和等于（ ） A1800 B1660 C1440 D1200 5 （2 分） （2018 秋资源县期中）实数 a，b，c 在数轴上的对应点的位置如图所示，如果 a+b0，那么下列结论正确的是（ ） A Ba+c0 Cabc0 D 6 （2 分） （2022拱墅区模拟）在一个不透明纸箱中放有除了数字不同外，其它完全相同的 2 张卡片，分别标有数字 1、2，从中任意摸出一张，放回搅匀后再任意摸出一张，两次摸出的数字之和为
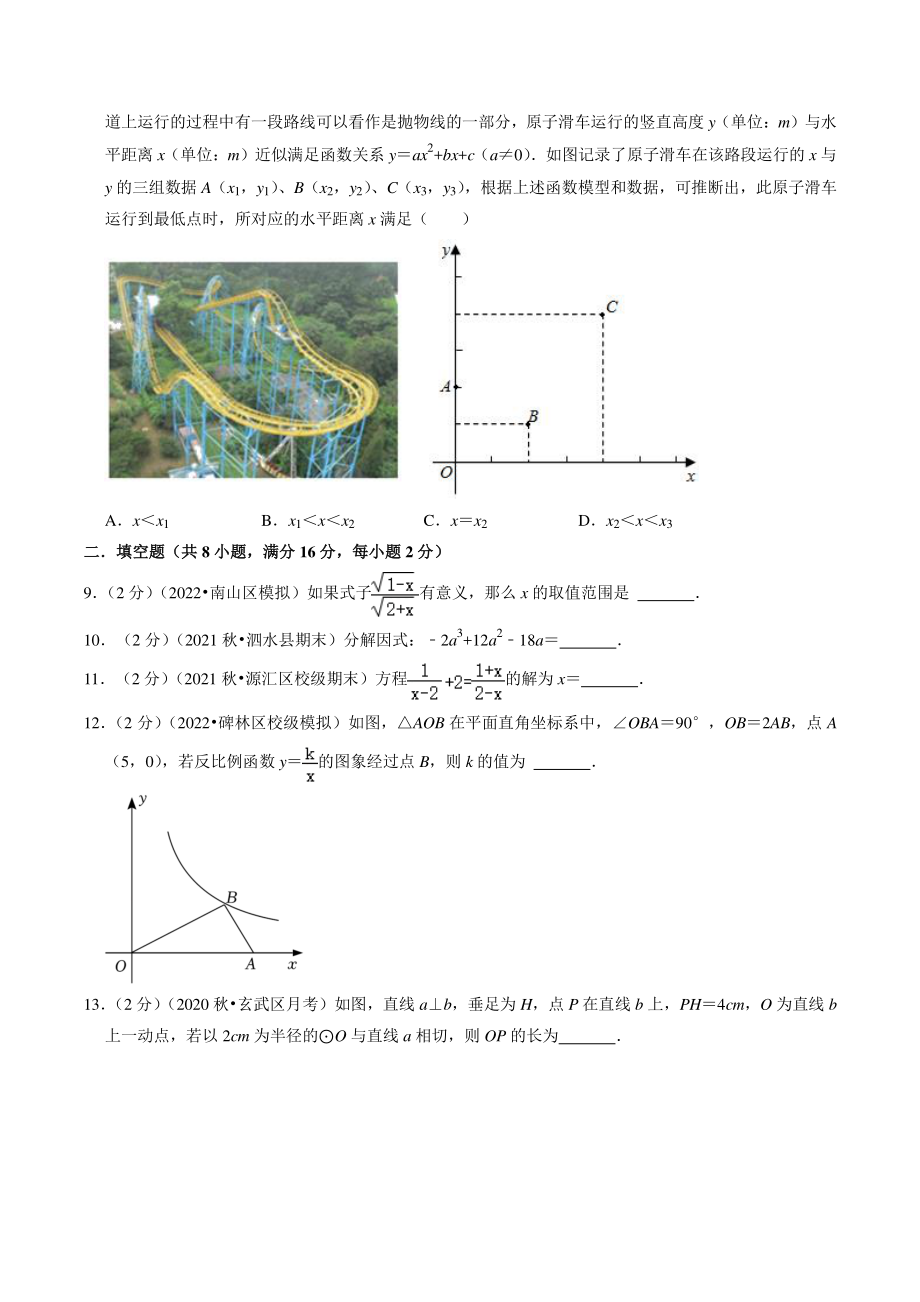
3、奇数的概率为（ ） A B C D 7 （2 分） （2021鹿城区校级二模）与+1 最接近的整数是（ ） A4 B5 C6 D8 8 （2 分） （2022建湖县一模）如图，游乐园里的原子滑车是很多人喜欢的项目，惊险刺激，原子滑车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分，原子滑车运行的竖直高度 y（单位：m）与水平距离 x（单位：m）近似满足函数关系 yax2+bx+c（a0） 如图记录了原子滑车在该路段运行的 x 与y 的三组数据 A（x1，y1） 、B（x2，y2） 、C（x3，y3） ，根据上述函数模型和数据，可推断出，此原子滑车运行到最低点时，所对应的水平距离 x 满足
4、（ ） Axx1 Bx1xx2 Cxx2 Dx2xx3 二填空题（共二填空题（共 8 小题，满分小题，满分 16 分，每小题分，每小题 2 分）分） 9 （2 分） （2022南山区模拟）如果式子有意义，那么 x 的取值范围是 10（2 分） （2021 秋泗水县期末）分解因式：2a3+12a218a 11（2 分） （2021 秋源汇区校级期末）方程的解为 x 12 （2 分） （2022碑林区校级模拟）如图，AOB 在平面直角坐标系中，OBA90，OB2AB，点 A（5，0） ，若反比例函数 y的图象经过点 B，则 k 的值为 13 （2 分） （2020 秋玄武区月考）如图，直线 ab，
5、垂足为 H，点 P 在直线 b 上，PH4cm，O 为直线 b上一动点，若以 2cm 为半径的O 与直线 a 相切，则 OP 的长为 14 （2 分） （2021桃江县模拟）如图，矩形 ABCD 中，AC，BD 相交于点 O，过点 B 作 BFAC 交 CD 于点 F，交 AC 于点 M，过点 D 作 DEBF 交 AB 于点 E，交 AC 于点 N，连接 FN，EM则下列结论： DNBM；EMFN；AEFC；当 AOAD 时，四边形 DEBF 是菱形 其中，正确的序号为： 15 （2 分） （2020 秋兴庆区校级期末）某校组织了一次比赛，甲、乙两队各有 5 人参加比赛，两队每人的比赛成绩（
6、单位：分）如下： 甲队：7，8，9，6，10 乙队：10，9，5，8，8 已知甲队成绩的方差为 S甲22，则成绩波动较大的是 队 16 （2 分）甲、乙两队修建一条水渠，甲先完成工程的三分之一，乙后完成工程的三分之二，两队所用的天数为 A；甲先完成工程的三分之二，乙后完成工程的三分之一，两队所用天数为 B；甲、乙两队同时工作完成的天数为 C，已知 A 比 B 多 5，A 是 C 的 2 倍多 4，那么甲单独完成此项工程需要 天 三解答题（共三解答题（共 12 小题，满分小题，满分 68 分）分） 17 （5 分） （2021 秋林甸县期末）计算： （3.14）0+2tan60（2）2021 （
7、）2020 18 （5 分） （2021 秋杜尔伯特县期末）解不等式组： 19 （5 分） （2021 秋沈丘县期末）先化简，再求值： （x2y）2+（x2y） （x+2y）2x（2xy）2x，其中 x1，y2 20 （5 分） （2022 春朝阳区校级月考）在 68 的正方形网格，每个小正方形的顶点称为格点，已知线段AB，其中点 A 在直线 MN 上请用无刻度的直尺按要求作图，保留作图痕迹 （1）在图中，在直线 MN 上找到一点 C，作ABC，使得ACB45； （2）在图中，在直线 MN 上找到一点 D，作ABD，使得ABD45； （3）在图中，在直线 MN 上找到一点 E，作ABE，使得E
8、ABEBA 21 （6 分） （2021南充）已知关于 x 的一元二次方程 x2（2k+1）x+k2+k0 （1）求证：无论 k 取何值，方程都有两个不相等的实数根 （2）如果方程的两个实数根为 x1，x2，且 k 与都为整数，求 k 所有可能的值 22 （6 分） （2022海淀区校级模拟）如图，在四边形 ABCD 中，ACBCAD90，ADBC，点 E在 BC 延长线上，AE 与 CD 交于点 F （1）求证：四边形 ABCD 是平行四边形； （2）若 AE 平分BAD，AB13，cosB，求 AD 和 CF 的长 23 （5 分） （2021 秋东城区校级期中）在平面直角坐标系 xOy
9、中，一次函数 ykx+b（k0）的图象由函数的图象向下平移 2 个单位长度得到 （1）求这个一次函数的解析式； （2）当 x4 时，对于 x 的每一个值，函数 ymx（m0）的值大于一次函数 ykx+b 的值，直接写出 m 的取值范围 24 （6 分） （2020 秋饶平县校级期末）如图，ABC 内接于O，AB 是O 的直径，C 是中点，弦 CEAB 于点 H，连接 AD，分别交 CE、BC 于点 P、Q，连接 BD （1）求证：P 是线段 AQ 的中点； （2）若O 的半径为 5，D 是的中点，求弦 CE 的长 25 （5 分） （2021 春襄汾县期末）某校为了解七、八年级学生对“防溺水”
10、安全知识的掌握情况，从七、八年级各随机抽取 50 名学生进行测试，并对成绩（百分制）进行整理和分析部分信息如下： a七年级成绩频数分布直方图； b七年级成绩在 70 x80 这一组的是： 70 72 74 75 76 76 77 77 77 78 79 c七、八年级成绩的平均数、中位数如下： 年级 平均数 中位数 七 76.9 m 八 79.2 79.5 根据以上信息，回答下列问题： （1）在这次测试中，七年级在 80 分以上（含 80 分）的有 人； （2）表中 m 的值为 ； （3）在这次测试中，七年级学生甲与八年级学生乙的成绩都是 78 分，请判断两位学生在各自年级的排名谁更靠前，并说明
11、理由 26 （6 分） （2021 春海曙区校级期末）已知抛物线 yax22x+1（a0）的对称轴为直线 x1 （1）a ； （2）若抛物线的顶点为 P，直线 y9 与抛物线交于两点 G、H，求PGH 的面积； （3）设直线 ym（m0）与抛物线 yax22x+1 交于点 A、B，与抛物线 y4（x1）2交于点 C，D，则线段 AB 与线段 CD 的长度之比为 27 （7 分） （2022沙坪坝区校级开学）如图，ABC 为等腰三角形，ABAC，将 CA 绕点 C 顺时针旋转至CD，连接 AD，E 为直线 CD 上一点，连接 AE （1）如图 1，若BAC60，ACD90，E 为 CD 中点，A
12、B2，求BCE 的面积； （2）如图 2，若ACD90，点 E 在线段 CD 上且DAE+ABC90，AE 的延长线与 BC 的延长线交于点 F，连接 DF，求证：BCDF 28 （7 分） （2021 秋晋州市期末）如图： （1） 【问题发现】 如图 1，ABC 内接于半径为 4 的O，若C60，则 AB ； （2） 【问题探究】 如图 2，四边形 ABCD 内接于半径为 6 的O，若B120，求四边形 ABCD 的面积最大值； （3） 【解决问题】 如图 3，一块空地由三条直路（线段 AD、AB、BC）和一条弧形道路围成，点 M 是 AB 道路上的一个地铁站口，已知 ADBM1 千米，AM
13、BC2 千米，AB60，的半径为 1 千米，市政府准备将这块空地规划为一个公园， 主入口在点 M 处， 另外三个入口分别在点 C、 D、 P 处， 其中点 P 在上，并在公园中修四条慢跑道，即图中的线段 DM、MC、CP、PD，是否存在一种规划方案，使得四条慢跑道总长度（即四边形 DMCP 的周长）最大？若存在，求其最大值；若不存在，说明理由 参考答案解析参考答案解析 一选择题（共一选择题（共 8 小题，满分小题，满分 16 分，每小题分，每小题 2 分）分） 1 （2 分） （2020金坛区二模）若一个几何体的表面展开图如图所示，则这个几何体是（ ） A三棱柱 B四棱柱 C三棱锥 D四棱锥
14、【考点】几何体的展开图 【专题】几何图形；空间观念 【分析】由平面图形的折叠及立体图形的表面展开图的特点解题 【解答】解：三个长方形和两个三角形折叠后可以围成三棱柱 故选：A 【点评】考查了几何体的展开图，熟记常见几何体的表面展开图特征，是解决此类问题的关键 2 （2 分） （2022宿州一模）电影长津湖2021 年 9 月 30 日上映以来，据有关票房数据显示，截止到 10月 7 日，总票房达 46.49 亿将数据 46.49 亿用科学记数法表示为（ ） A46.49108 B4.649108 C4.649109 D0.46491010 【考点】科学记数法表示较大的数 【专题】实数；数感 【
15、分析】科学记数法的表示形式为 a10n的形式，其中 1|a|10，n 为整数确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同当原数绝对值10 时，n是正整数；当原数的绝对值1 时，n 是负整数 【解答】解：46.49 亿46490000004.649109 故选：C 【点评】此题考查科学记数法的表示方法科学记数法的表示形式为 a10n的形式，其中 1|a|10，n为整数，正确确定 a 的值以及 n 的值是解决问题的关键 3 （2 分） （2022海淀区校级模拟）如图，点 O 在直线 AB 上，OCOD若BOC60，则AOD 的大小为（ ） A16
16、0 B140 C120 D150 【考点】垂线 【专题】线段、角、相交线与平行线；几何直观；运算能力 【分析】根据垂直的定义可得BOC90，进而求出BOD，再根据平角的定义求出答案 【解答】解：OCOD COD90， BOC60， BOD906030， 又AOD+BOD180， AOD18030150， 故选：D 【点评】本题考查垂线，角的计算，理解垂直的定义以及角的和差关系是正确解答的前提 4 （2 分） （2021云南）一个十边形的内角和等于（ ） A1800 B1660 C1440 D1200 【考点】多边形内角与外角 【专题】多边形与平行四边形；推理能力 【分析】根据多边形的内角和等于
17、（n2） 180即可得解 【解答】解：根据多边形内角和公式得， 十边形的内角和等于： （102）18081801440， 故选：C 【点评】此题考查了多边形的内角，熟记多边形的内角和公式是解题的关键 5 （2 分） （2018 秋资源县期中）实数 a，b，c 在数轴上的对应点的位置如图所示，如果 a+b0，那么下列结论正确的是（ ） A Ba+c0 Cabc0 D 【考点】实数与数轴；绝对值 【专题】实数；运算能力；推理能力 【分析】由 a+b0 可以得出 a、b 互为相反数，从而得出 a0bc，|a|b|c|即可作出判断 【解答】解：a+b0， a、b 互为相反数，a0bc，|a|b|c|，
18、 A 选项错误； a+c 要取绝对值较大的数的符号， a+c0， B 选项错误； a0bc， abc0， C 选项正确； a、b 互为相反数， 1， D 选项错误， 故选：C 【点评】本题主要考查数轴的性质，关键是要牢记数轴上的点从左到右依次增大，到原点的距离越小的数的绝对值越小 6 （2 分） （2022拱墅区模拟）在一个不透明纸箱中放有除了数字不同外，其它完全相同的 2 张卡片，分别标有数字 1、2，从中任意摸出一张，放回搅匀后再任意摸出一张，两次摸出的数字之和为奇数的概率为（ ） A B C D 【考点】列表法与树状图法 【专题】概率及其应用；数据分析观念；推理能力 【分析】画树状图，共
19、有 4 种等可能的结果，两次摸出的数字之和为奇数的结果有 2 种，再由概率公式求解即可 【解答】解：画树状图如下： 共有 4 种等可能的结果，两次摸出的数字之和为奇数的结果有 2 种， 两次摸出的数字之和为奇数的概率为， 故选：C 【点评】此题主要考查了树状图法求概率，树状图法可以不重复不遗漏的列出所有可能的结果，适用于两步或两步以上完成的事件；解题时还要注意是放回试验还是不放回试验用到的知识点为：概率所求情况数与总情况数之比 7 （2 分） （2021鹿城区校级二模）与+1 最接近的整数是（ ） A4 B5 C6 D8 【考点】估算无理数的大小 【专题】实数；二次根式；运算能力 【分析】先估
20、算出的范围，再求出+1 的范围，最后得出选项即可 【解答】解：3.54， 4.5+15， 与+1 最接近的整数是 5， 故选：B 【点评】本题考查了实数的大小比较和估算无理数的大小，能估算出的范围是解此题的关键 8 （2 分） （2022建湖县一模）如图，游乐园里的原子滑车是很多人喜欢的项目，惊险刺激，原子滑车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分，原子滑车运行的竖直高度 y（单位：m）与水平距离 x（单位：m）近似满足函数关系 yax2+bx+c（a0） 如图记录了原子滑车在该路段运行的 x 与y 的三组数据 A（x1，y1） 、B（x2，y2） 、C（x3，y3） ，根据上
21、述函数模型和数据，可推断出，此原子滑车运行到最低点时，所对应的水平距离 x 满足（ ） Axx1 Bx1xx2 Cxx2 Dx2xx3 【考点】二次函数的应用 【专题】二次函数图象及其性质；几何直观；运算能力 【分析】将点 A（0，2） 、B（2，1） 、C（4，4）分别代入函数解析式，求得系数的值；然后由抛物线的对称轴公式可以得到答案 【解答】解：根据题意知，抛物线 yax2+bx+c（a0）经过点 A（0，2） 、B（2，1） 、C（4，4） ， 则， 解得：， 所以 x 此原子滑车运行到最低点时，所对应的水平距离 x 满足 x1xx2 故选：B 【点评】 此题考查了二次函数的应用， 此题
22、也可以将所求得的抛物线解析式利用配方法求得顶点式方程，然后直接得到抛物线顶点坐标，由顶点坐标推知此原子滑车运行到最低点时，所对应的水平距离 二填空题（共二填空题（共 8 小题，满分小题，满分 16 分，每小题分，每小题 2 分）分） 9 （2 分） （2022南山区模拟）如果式子有意义，那么 x 的取值范围是 2x1 【考点】二次根式有意义的条件 【专题】分式；二次根式；运算能力 【分析】根据被开方数大于等于 0，分母不等于 0 列式计算即可得解 【解答】解：由题意得， ， 解得2x1 故答案为：2x1 【点评】本题考查的知识点为：分式有意义，分母不为 0；二次根式的被开方数是非负数 10（2
23、 分） （2021 秋泗水县期末）分解因式：2a3+12a218a 2a（a3）2 【考点】提公因式法与公式法的综合运用 【专题】整式；运算能力 【分析】先提公因式，然后再利用完全平方公式继续分解即可 【解答】解：2a3+12a218a 2a（a26a+9） 2a（a3）2， 故答案为：2a（a3）2 【点评】本题考查了提公因式法与公式法的综合运用，一定要注意如果多项式的各项含有公因式，必须先提公因式 11 （2 分） （2021 秋源汇区校级期末）方程的解为 x 【考点】解分式方程 【专题】分式方程及应用；运算能力 【分析】按照解分式方程的步骤进行计算即可解答 【解答】解：， 1+2（x2）
24、1x， 解得：x， 检验：当 x时，x20， x是原方程的根 【点评】本题考查了解分式方程，一定要注意解分式方程必须检验 12 （2 分） （2022碑林区校级模拟）如图，AOB 在平面直角坐标系中，OBA90，OB2AB，点 A（5，0） ，若反比例函数 y的图象经过点 B，则 k 的值为 8 【考点】反比例函数图象上点的坐标特征 【专题】反比例函数及其应用；运算能力；推理能力 【分析】作 BDOA 于 D，设 B（m，n） ，则 ODm，BDn，AD5m，证得OBDBAD，得到，解得 m4，n2， 然后利用待定系数法即可求得 k 的值 【解答】解：作 BDOA 于 D， OBA90， OB
25、D+ABD90， ABD+DAB90， OBDBAD， ODBBDA90， OBDBAD， ， 设 B（m，n） ，则 ODm，BDn， OB2AB，点 A（5，0） ， AD5m， ， 解得 m4，n2， B（4，2）， 反比例函数 y的图象经过点 B， k428， 故答案为：8 【点评】本题考查了反比例图象上点的坐标特征，三角形相似的判断和性质，求得 B 的坐标是解题的关键 13 （2 分） （2020 秋玄武区月考）如图，直线 ab，垂足为 H，点 P 在直线 b 上，PH4cm，O 为直线 b上一动点，若以 2cm 为半径的O 与直线 a 相切，则 OP 的长为 2cm 或 6cm 【
26、考点】切线的性质 【专题】与圆有关的位置关系；几何直观；推理能力 【分析】当点 O 在点 H 的左侧O 与直线 a 相切时，OPPHOH；当点 O 在点 H 的右侧O 与直线a 相切时，OPPH+OH，即可得出结果 【解答】解：直线 ab，O 为直线 b 上一动点， O 与直线 a 相切时，切点为 H， OH2cm， 当点 O 在点 H 的左侧，O 与直线 a 相切时，如图 1 所示： OPPHOH422（cm）； 当点 O 在点 H 的右侧，O 与直线 a 相切时，如图 2 所示： OPPH+OH4+26（cm）； O 与直线 a 相切，OP 的长为 2cm 或 6cm， 故答案为：2cm
27、或 6cm 【点评】本题考查了切线的性质以及分类讨论；熟练掌握切线的性质是解题的关键 14 （2 分） （2021桃江县模拟）如图，矩形 ABCD 中，AC，BD 相交于点 O，过点 B 作 BFAC 交 CD 于点 F，交 AC 于点 M，过点 D 作 DEBF 交 AB 于点 E，交 AC 于点 N，连接 FN，EM则下列结论： DNBM；EMFN；AEFC；当 AOAD 时，四边形 DEBF 是菱形 其中，正确的序号为： 【考点】矩形的性质；全等三角形的判定与性质；菱形的性质；菱形的判定 【专题】图形的全等；等腰三角形与直角三角形；矩形 菱形 正方形；推理能力 【分析】 证DNABMC
28、（AAS） ， 得出 DNBM， ADECBF， 故正确； 证ADECBF （ASA） ，得出 AEFC，DEBF，故正确；证四边形 NEMF 是平行四边形，得出 EMFN，故正确；证四边形 DEBF 是平行四边形，证出ODNABD，则 DEBE，得出四边形 DEBF 是菱形；故正确；即可得出结论 【解答】解：四边形 ABCD 是矩形， ABCD，ABCD，DAEBCF90，ODOBOAOC，ADBC，ADBC， DANBCM， BFAC，DEBF， DEAC， DNABMC90， 在DNA 和BMC 中， ， DNABMC（AAS）， DNBM，ADECBF，故正确； 在ADE 和CBF 中
29、， ， ADECBF（ASA）， AEFC，DEBF，故正确； DEDNBFBM，即 NEMF， DEBF， 四边形 NEMF 是平行四边形， EMFN，故正确； ABCD，AECF， BEDF， BEDF， 四边形 DEBF 是平行四边形， AOAD， AOADOD， AOD 是等边三角形， ADODAN60， ABD90ADO30， DEAC， ADNODN30， ODNABD， DEBE， 四边形 DEBF 是菱形；故正确； 故答案为： 【点评】本题考查了矩形的性质、菱形的判定、平行四边形的判定与性质、全等三角形的判定与性质、等边三角形的判定与性质、等腰三角形的判定等知识；熟练掌握矩形的
30、性质和菱形的判定，证明三角形全等是解题的关键 15 （2 分） （2020 秋兴庆区校级期末）某校组织了一次比赛，甲、乙两队各有 5 人参加比赛，两队每人的比赛成绩（单位：分）如下： 甲队：7，8，9，6，10 乙队：10，9，5，8，8 已知甲队成绩的方差为 S甲22，则成绩波动较大的是 乙 队 【考点】方差 【专题】统计的应用；运算能力 【分析】先由平均数的公式计算出乙队的平均成绩，再根据方差的公式求出乙队的方差，然后根据方差的意义即可得出答案 【解答】解：乙队的平均成绩为（10+9+5+8+8）8（分） ， 其方差 S2乙（108）2+（98）2+（58）2+（88）2+（88）22.8
31、 22.8，即 S2甲S2乙， 乙队成绩波动较大 故答案为：乙 【点评】本题考查方差的定义：一般地设 n 个数据，x1，x2，xn的平均数为 ，则方差 S2（x1 ）2+（x2 ）2+（xn ）2，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立 16 （2 分）甲、乙两队修建一条水渠，甲先完成工程的三分之一，乙后完成工程的三分之二，两队所用的天数为 A；甲先完成工程的三分之二，乙后完成工程的三分之一，两队所用天数为 B；甲、乙两队同时工作完成的天数为 C，已知 A 比 B 多 5，A 是 C 的 2 倍多 4，那么甲单独完成此项工程需要 30 天 【考点】一元一次方程的应用；二元
32、一次方程的应用；列代数式 【专题】分式；一次方程（组）及应用；应用意识 【分析】设甲单独完成此项工程需要 x 天，乙单独完成此项工程需要 y 天，则 A+，B+，C，由 A 比 B 多 5，可得出关于 x，y 的二元一次方程，化简后可得出 yx+15，结合是 C 的 2倍多 4，即可得出关于 x 的一元一次方程，解之即可得出结论 【解答】解：设甲单独完成此项工程需要 x 天，乙单独完成此项工程需要 y 天，则 A+，B+，C 依题意得：+（+）5， yx+15 A 是 C 的 2 倍多 4， +2+4， 化简得：3x900， 解得：x30， 经检验，x30 是原方程的解，且符合题意， 甲单独完
33、成此项工程需要 30 天 故答案为：30 【点评】 本题考查了一元一次方程的应用、 二元一次方程的应用以及列代数式， 根据各数量之间的关系，用含 x 的代数式表示出 A，B，C 是解题的关键 三解答题（共三解答题（共 12 小题，满分小题，满分 68 分）分） 17 （5 分） （2021 秋林甸县期末）计算： （3.14）0+2tan60（2）2021 （）2020 【考点】实数的运算；零指数幂；特殊角的三角函数值 【专题】实数；运算能力 【分析】根据零指数幂的意义、立方根的性质、特殊角的锐角三角函数的值以及有理数的乘方运算即可求出答案 【解答】解：原式1+（2）+2（2）2020（）202
34、0（2） 12+6（2）2020（2） 12+61（2） 12+6+2 7 【点评】本题考查实数的运算，解题的关键熟练运用零指数幂的意义、立方根的性质、特殊角的锐角三角函数的值以及有理数的乘方运算，本题属于基础题型 18 （5 分） （2021 秋杜尔伯特县期末）解不等式组： 【考点】解一元一次不等式组 【专题】一元一次不等式（组）及应用；运算能力 【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集 【解答】解：解不等式 2x+53（x+2），得：x1， 解不等式 2x1，得：x3， 则不等式组的解集为1x3 【点评】本题考查的是
35、解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键 19 （5 分） （2021 秋沈丘县期末）先化简，再求值： （x2y）2+（x2y） （x+2y）2x（2xy）2x，其中 x1，y2 【考点】整式的混合运算化简求值 【专题】整式；运算能力 【分析】原式中括号里利用完全平方公式，平方差公式，以及单项式乘多项式法则计算，去括号合并后利用多项式除以单项式法则计算得到最简结果，把 x 与 y 的值代入计算即可求出值 【解答】解：原式（x24xy+4y2+x24y24x2+2xy）2x （2x22xy）2x xy，
36、当 x1，y2 时，原式1+21 【点评】此题考查了整式的混合运算化简求值，熟练掌握运算法则是解本题的关键 20 （5 分） （2022 春朝阳区校级月考）在 68 的正方形网格，每个小正方形的顶点称为格点，已知线段AB，其中点 A 在直线 MN 上请用无刻度的直尺按要求作图，保留作图痕迹 （1）在图中，在直线 MN 上找到一点 C，作ABC，使得ACB45； （2）在图中，在直线 MN 上找到一点 D，作ABD，使得ABD45； （3）在图中，在直线 MN 上找到一点 E，作ABE，使得EABEBA 【考点】作图应用与设计作图；等腰三角形的性质 【专题】作图题；几何直观 【分析】 （1）利用
37、等腰直角三角形的性质（图中BCR 是等腰直角三角形） ，解决问题即可； （2）构造等腰直角三角形，可得结论； （3）作线段 AB 的垂直平分线交 MN 于点 E，连接 EB，ABE 即为所求 【解答】解： （1）如图中，ACB 即为所求； （2）如图中，ABD 即为所求； （3）如图中，ABE 即为所求 【点评】本题考查作图应用与设计作图，等腰直角三角形的判定和性质，线段的垂直平分线的性质等知识，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型 21 （6 分） （2021南充）已知关于 x 的一元二次方程 x2（2k+1）x+k2+k0 （1）求证：无论 k 取何值，方程都有两个
38、不相等的实数根 （2）如果方程的两个实数根为 x1，x2，且 k 与都为整数，求 k 所有可能的值 【考点】解一元二次方程因式分解法；根的判别式 【专题】一元二次方程及应用；运算能力 【分析】 （1）根据方程的系数结合根的判别式，可得出10，进而可证出方程有两个不相等的实数根； （2）解方程求出方程的两根为 k，k+1，得出1+或1，然后利用有理数的整除性确定k 的整数值； 【解答】 （1）证明：（2k+1）24（k2+k）10， 无论 k 取何值，方程有两个不相等的实数根 （2）解：x2（2k+1）x+k2+k0，即（xk）x（k+1）0， 解得：xk 或 xk+1 一元二次方程 x2（2k
39、+1）x+k2+k0 的两根为 k，k+1， 或， 如果 1+为整数，则 k 为 1 的约数， k1， 如果 1为整数，则 k+1 为 1 的约数， k+11， 则 k 为 0 或2 整数 k 的所有可能的值为1，0 或2 【点评】本题考查了根的判别式、解一元二次方程，解题的关键是： （1）牢记“当0 时，方程有两个不相等的实数根” ； （2）利用解方程求出 k 的整数值 22 （6 分） （2022海淀区校级模拟）如图，在四边形 ABCD 中，ACBCAD90，ADBC，点 E在 BC 延长线上，AE 与 CD 交于点 F （1）求证：四边形 ABCD 是平行四边形； （2）若 AE 平分B
40、AD，AB13，cosB，求 AD 和 CF 的长 【考点】平行四边形的判定与性质；解直角三角形；勾股定理 【专题】线段、角、相交线与平行线；等腰三角形与直角三角形；多边形与平行四边形；解直角三角形及其应用；运算能力；推理能力 【分析】 （1）先证 ADBC，再由 ADBC，即可得出结论； （2）由锐角三角函数定义得 BC5，再由平行四边形的性质得 ADBC5，然后证 BEAB13，则CEBEBC8，进而证CFEBEA，得 CFCE8 【解答】 （1）证明：ACBCAD90， ADBC， ADBC， 四边形 ABCD 是平行四边形； （2）解：ACB90，AB13， cosB， BC5， 由（
41、1）可知，四边形 ABCD 是平行四边形， ADBC5，ABCD，ADBC， DAEBEA， AE 平分BAD， DAEBAE， BEABAE， BEAB13， CEBEBC1358， ABCD， CFEBAE， CFEBEA， CFCE8 【点评】本题考查了平行四边形的判定与性质、等腰三角形的判定、锐角三角函数定义、平行线的判定与性质等知识，熟练掌握平行四边形的判定与性质是解题的关键 23 （5 分） （2021 秋东城区校级期中）在平面直角坐标系 xOy 中，一次函数 ykx+b（k0）的图象由函数的图象向下平移 2 个单位长度得到 （1）求这个一次函数的解析式； （2）当 x4 时，对于
42、 x 的每一个值，函数 ymx（m0）的值大于一次函数 ykx+b 的值，直接写出 m 的取值范围 【考点】一次函数图象与几何变换；一次函数图象与系数的关系 【专题】一次函数及其应用；几何直观；应用意识 【分析】 （1）根据平移的规律即可求得 （2）根据点（4，4）结合图象即可求得 【解答】解： （1）函数的图象向下平移 2 个单位长度得到 yx2， 一次函数 ykx+b（k0）的图象由函数的图象向下平移 2 个单位长度得到， 这个一次函数的表达式为 yx2 （2）把 x4 代入 yx2，求得 y4， 函数 ymx（m0）与一次函数 yx2 的交点为（4，4） ， 把点（4，4）代入 ymx，
43、求得 m1， 当 x4 时，对于 x 的每一个值，函数 ymx（m0）的值大于一次函数 yx2 的值， m1 【点评】本题考查了一次函数图象与几何变换，一次函数与系数的关系，数形结合是解题的关键 24 （6 分） （2020 秋饶平县校级期末）如图，ABC 内接于O，AB 是O 的直径，C 是中点，弦 CEAB 于点 H，连接 AD，分别交 CE、BC 于点 P、Q，连接 BD （1）求证：P 是线段 AQ 的中点； （2）若O 的半径为 5，D 是的中点，求弦 CE 的长 【考点】三角形的外接圆与外心；勾股定理；垂径定理；圆心角、弧、弦的关系；圆周角定理 【专题】圆的有关概念及性质；推理能力
44、 【分析】 （1）利用垂径定理得到，则可证明，利用圆周角定理得到CADACE，所以APCP，再证明BCPCQA 得到 CPPQ，于是得到 APPQ； （2）利用，AB 是直径，利用圆周角得到ACB90，ABC30，然后利用含 30 度的直角三角形三边的关系计算出 CH，而根据垂径定理得到 CHEH，于是可得 CE 的长度 【解答】 （1）证明：CEAB，AB 是直径， ， 又 ， CADACE， APCP， AB 是O 的直径， ACB90， ACE+BCP90，CAD+CQA90， BCPCQA， CPPQ， APPQ， 即 P 是线段 AQ 的中点； （2）解：，AB 是直径， ACB90
45、，ABC30， 又AB5210， AC5，BC5， CHBC， 又CEAB， CHEH， CE2CH25 【点评】本题考查了三角形的外接圆与外心：三角形外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心也考查了垂径定理和圆周角定理 25 （5 分） （2021 春襄汾县期末）某校为了解七、八年级学生对“防溺水”安全知识的掌握情况，从七、八年级各随机抽取 50 名学生进行测试，并对成绩（百分制）进行整理和分析部分信息如下： a七年级成绩频数分布直方图； b七年级成绩在 70 x80 这一组的是： 70 72 74 75 76 76 77 77 77 78 79 c七、八年级成绩的平均数
46、、中位数如下： 年级 平均数 中位数 七 76.9 m 八 79.2 79.5 根据以上信息，回答下列问题： （1）在这次测试中，七年级在 80 分以上（含 80 分）的有 23 人； （2）表中 m 的值为 77.5 ； （3）在这次测试中，七年级学生甲与八年级学生乙的成绩都是 78 分，请判断两位学生在各自年级的排名谁更靠前，并说明理由 【考点】频数（率）分布直方图；加权平均数；中位数 【专题】统计的应用；数据分析观念；运算能力 【分析】 （1）求出 80 x90，90 x100 两组的频数之和即可； （2）根据中位数的意义求出中间位置两个数的平均数即可； （3）根据中位数的意义，结合七年
47、级的甲同学，八年级的乙同学的成绩进行判断即可 【解答】解：（1）15+823（人）， 故答案为：23； （2）将七年级 50 人的成绩从小到大排列后，处在中间位置的两个数的平均数为77.5（分） ，因此中位数是 77.5 分，即 m77.5， 故答案为：77.5； （3）七年级学生甲的排名更靠前，理由为：七年级成绩的中位数是 77.5，甲同学的成绩 78 分，位于中位数以上，而八年级成绩的中位数是 79.5，乙同学的成绩 78 分，位于中位数以下，因此七年级同学甲的排名更靠前 【点评】本题考查频数分布直方图，加权平均数，中位数，理解中位数的意义是正确解答的前提 26 （6 分） （2021 春
48、海曙区校级期末）已知抛物线 yax22x+1（a0）的对称轴为直线 x1 （1）a 1 ； （2）若抛物线的顶点为 P，直线 y9 与抛物线交于两点 G、H，求PGH 的面积； （3）设直线 ym（m0）与抛物线 yax22x+1 交于点 A、B，与抛物线 y4（x1）2交于点 C，D，则线段 AB 与线段 CD 的长度之比为 2 【考点】二次函数的性质；二次函数图象上点的坐标特征 【专题】二次函数图象及其性质；推理能力 【分析】 （1）由抛物线对称轴直线方程 x求解 （2）求出点 G，H 坐标然后根据三角形面积公式求解 （3）分别将 ym 代入两抛物线解析式，求出 AB，CD 长度作商求解
49、【解答】解： （1）抛物线对称轴为直线 x1， a1 故答案为：1 （2）由（1）得 yx22x+1（x1）2， 点 P 坐标为（1，0） ， 把 y9 代入 yx22x+1 得 9x22x+1， 解得 x2 或 x4， G，H 坐标为（2，9） ， （4，9） ， SPGHGH（yGyP）（4+2）927 （3）yx22x+1（x1）2， 把 ym 代入 y（x1）2得 m（x1）2， 解得 x1+或 x1， AB1+（1）2 把 ym 代入 y4（x1）2得 m4（x1）2， 解得 x1+或 x1 CD1+（1）， 2 故答案为：2 【点评】本题考查二次函数的性质，解题关键是熟练掌握二次函
50、数的性质 27 （7 分） （2022沙坪坝区校级开学）如图，ABC 为等腰三角形，ABAC，将 CA 绕点 C 顺时针旋转至CD，连接 AD，E 为直线 CD 上一点，连接 AE （1）如图 1，若BAC60，ACD90，E 为 CD 中点，AB2，求BCE 的面积； （2）如图 2，若ACD90，点 E 在线段 CD 上且DAE+ABC90，AE 的延长线与 BC 的延长线交于点 F，连接 DF，求证：BCDF 【考点】旋转的性质；全等三角形的判定与性质 【专题】图形的全等；平移、旋转与对称；推理能力 【分析】 （1）由直角三角形的性质求出 EN，即可求解； （2）作 AGBC 于 G，作
