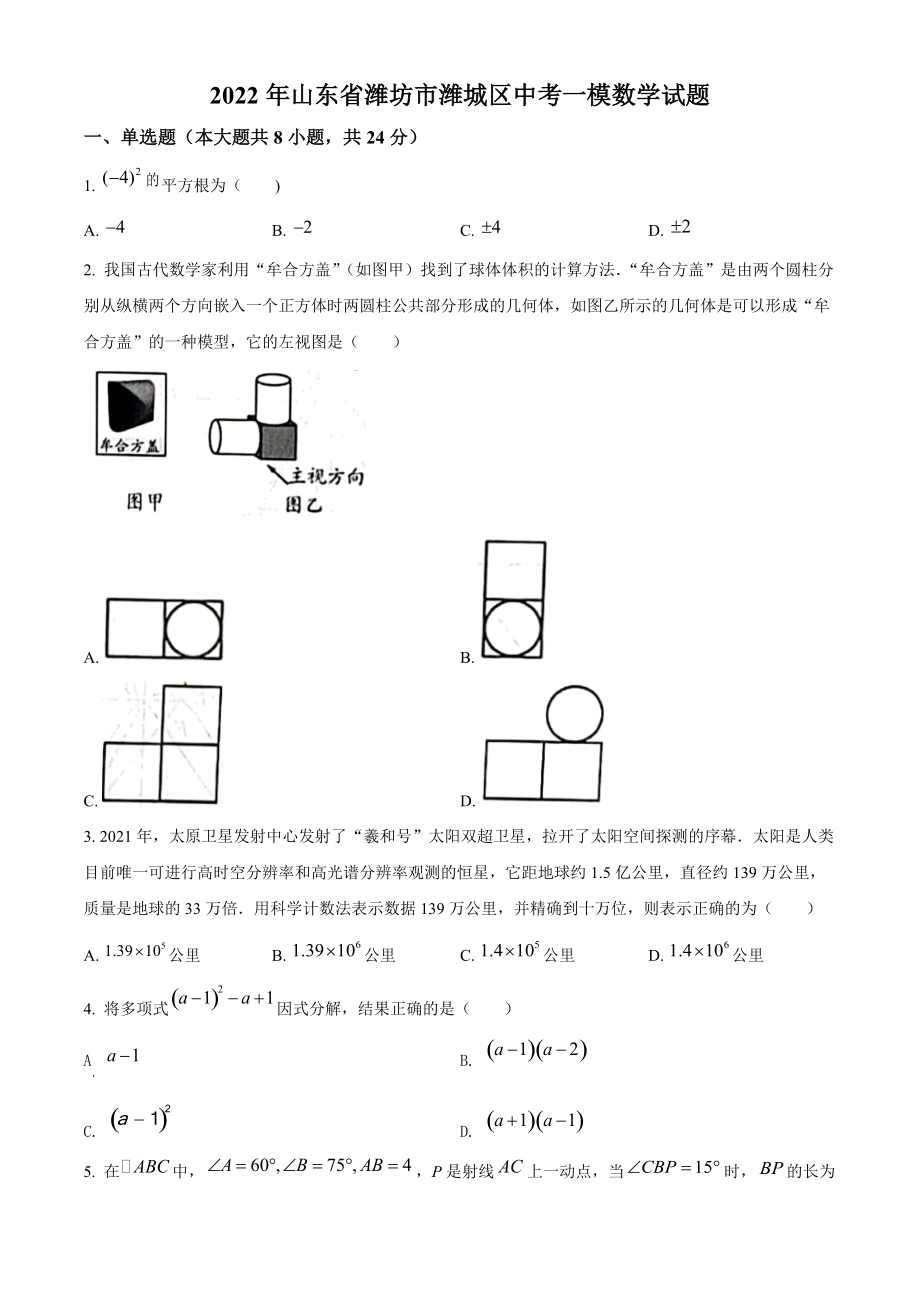
1、2022年山东省潍坊市潍城区中考一模数学试题一、单选题（本大题共8小题，共24分）1. 平方根为（ )A. B. C. D. 2. 我国古代数学家利用“牟合方盖”（如图甲）找到了球体体积的计算方法“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体，如图乙所示的几何体是可以形成“牟合方盖”的一种模型，它的左视图是（ ）A. B. C. D. 3. 2021年，太原卫星发射中心发射了“羲和号”太阳双超卫星，拉开了太阳空间探测的序幕太阳是人类目前唯一可进行高时空分辨率和高光谱分辨率观测的恒星，它距地球约1.5亿公里，直径约139万公里，质量是地球的33万倍用科学计数
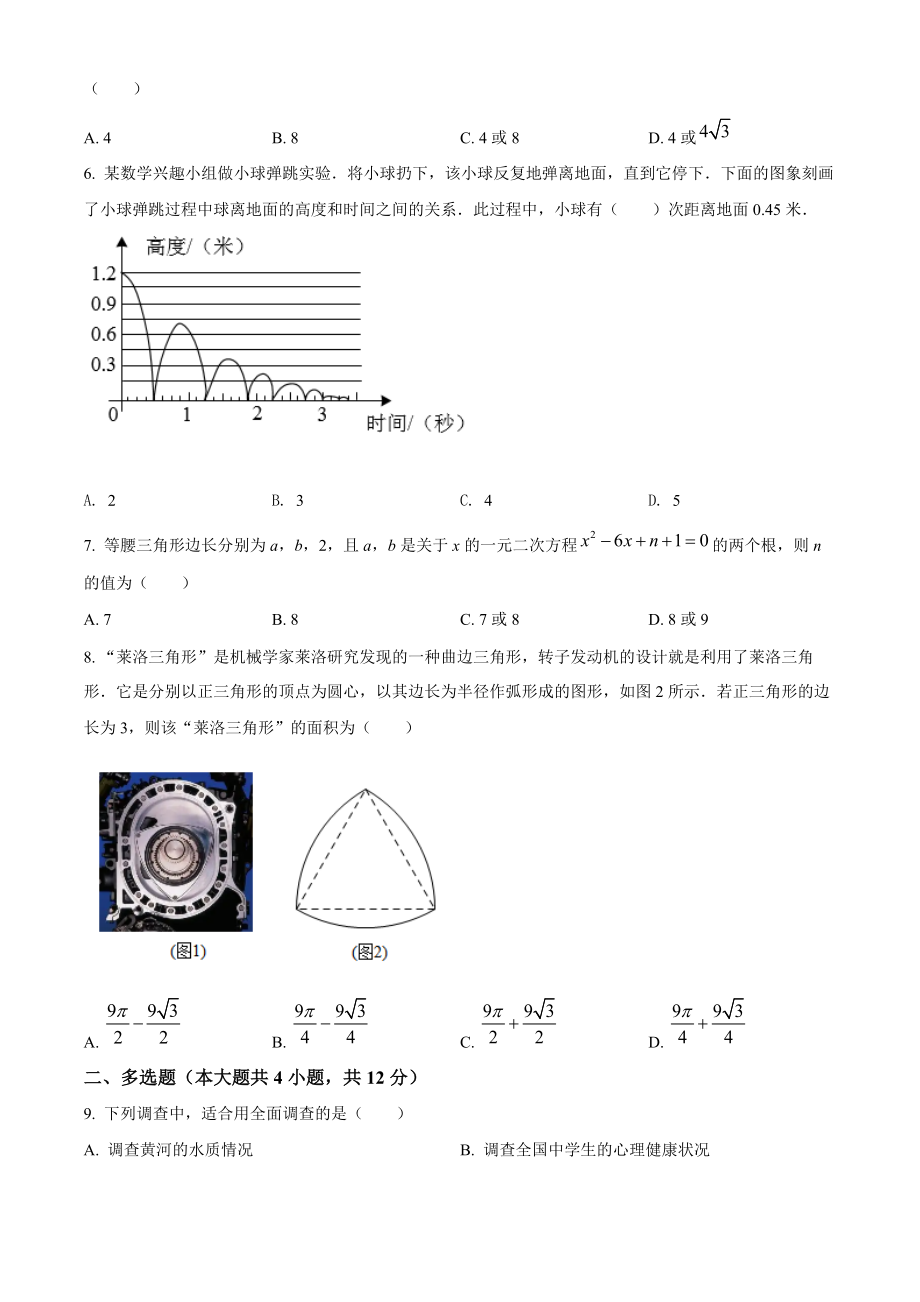
2、法表示数据139万公里，并精确到十万位，则表示正确的为（ ）A. 公里B. 公里C. 公里D. 公里4. 将多项式因式分解，结果正确的是（ ）A B. C. D. 5. 在中，P是射线上一动点，当时，的长为（ ）A. 4B. 8C. 4或8D. 4或6. 某数学兴趣小组做小球弹跳实验将小球扔下，该小球反复地弹离地面，直到它停下下面的图象刻画了小球弹跳过程中球离地面的高度和时间之间的关系此过程中，小球有（ ）次距离地面0.45米A. 2B. 3C. 4D. 57. 等腰三角形边长分别为a，b，2，且a，b是关于x的一元二次方程的两个根，则n的值为（ ）A. 7B. 8C. 7或8D. 8或98.
3、 “莱洛三角形”是机械学家莱洛研究发现的一种曲边三角形，转子发动机的设计就是利用了莱洛三角形它是分别以正三角形的顶点为圆心，以其边长为半径作弧形成的图形，如图2所示若正三角形的边长为3，则该“莱洛三角形”的面积为（ ）A. B. C. D. 二、多选题（本大题共4小题，共12分）9. 下列调查中，适合用全面调查的是（ ）A. 调查黄河的水质情况B. 调查全国中学生的心理健康状况C. 调查某班级40名学生的视力情况D. 某客运公司检测10辆客运汽车的安全性能10. 关于x的分式方程解的情况，下列说法正确的是（ )A. 若，则此方程无解B. 若，则此方程无解C. 若方程的解为负数，则D. 若，则方
4、程的解为正数11. 如图，已知，点E，F分别在直线上，且平分平分，与相交于点O，则下列结论正确的是（ ）A. B. C. D. 12. 在同一平面直角坐标系中，如图所示，正比例函数与一次函数的图象则二次函数的图象可能是（ ）A. B. C. D. 三、填空题（本大题共4小题，共12分）13. 计算的结果是_14. 云顶滑雪公园是北京2022年冬奥会7个雪上竞赛场馆中唯一利用现有雪场改造而成的下图左右两幅图分别是公园内云顶滑雪场U型池的实景图和示意图，该场地可以看作是从一个长方体中挖去了半个圆柱而成，它的横截面图中半圆的半径为，其边缘，点E在上，一名滑雪爱好者从点A滑到点E，他滑行的最短路线长为
5、_m15. 如图是一张四边形纸片，点M，N分别是，上的点，将沿直线翻折，将沿直线翻折，点A和点B落在同一点G处，再将纸片沿直线折叠，点C恰好落在点D处，则的长为_16. 如图，在平面直角坐标系中，点B的坐标为，轴，反比例函数的图象与交于点C，与交于点E，且，则点E的坐标为_四、解答题（本大题共7小题，共72分）17. 先化简，再求值：，其中a为不等式组的整数解18. 某移动公司为了提升网络信号，在坡度的山坡上加装了信号塔（如图所示），信号塔底端Q到坡底A的距离为3.9米为了提醒市民，在距离斜坡底A点5.4米的水平地面上立了一块警示牌，当太阳光线与水平线所成的夹角为时，信号塔顶端P的影子落在警示
6、牌上的点E处，且长为3米（1）求点Q到水平地面的铅直高度；（2）求信号塔的高度大约为多少米？（参考数据：）20. 某商场为掌握国庆节期间顾客购买商品时刻的分布情况，统计了10月1日7:00-23:00这一时间段内5000名顾客的购买时刻顾客购买商品时刻的频数分布直方图和扇形统计图如图所示，将7:00-23:00这一时间段划分为四个小的时间段：A段为，B段为，C段为，D段为，其中t为顾客购买商品的时刻，扇形统计图中，A，B，C，D四段各部分圆心角的度数比为1342请根据上述信息解答下列问题：（1）通过计算将频数直方图补充完整，并直接写出顾客购买商品时刻的中位数落在哪个时间段？（2）求10月1日这
7、天顾客购买商品时刻的平均值（同一时间段内顾客购买商品时刻的平均值用该时段的中点值代表例如，A段的中点值为：）；（3）活跃节日气氛，该商场设置购物后抽奖活动，设立了特等奖一个，一等奖两个，二等奖若干，并随机分配到A，B，C，D四个时间段中请直接写出特等奖出现在A时间段的概率；请利用画树状图或列表的方法，求两个一等奖出现在不同时间段的概率22. 如图，以的边为直径的交于点F，点E是的中点，连接并延长交于点D，若（1）求证：是的切线；（2）若半径为2，求的长24. 某公司生产的一种产品在市场上很受欢迎，该公司每年的产量为6万件，可在国内和国外两个市场全部销售若在国外销售，平均每件产品的利润（元）与国
8、外销售量x（万件）之间的函数关系如图所示若在国内销售，平均每件产品的利润为元，设该公司每年在国内和国外销售的总利润为w万元（1）求与x之间的函数表达式，并写出x的取值范围；（2）该公司每年在国内国外销售量各为多少时，可使公司每年的总利润最大？最大总利润是多少？26. 如图，二次函数经过菱形顶点A，B，D，且，点D的坐标为(0，4)，延长交抛物线于另一点E，连接，交于点F（1）求二次函数的表达式；（2）求的面积；（3）如图，直线l是二次函数图象的对称轴，若P为l上一点，且P，D，B三点构成以为底的等腰三角形，求点P的坐标28. 如图，矩形中，为等边三角形点E，F分别为边上的动点，且，P为上一动点
9、，连接，将线段绕点B顺时针旋转至，连接（1）求证：；（2）当三条线段的和最小时，求的长；（3）若点E以每秒2个单位的速度由A点向D点运动，点P以每秒1个单位的速度由E点向F点运动E，P两点同时出发，点E到达点D时停止，点P到达点F时停止，设点P的运动时间为t秒求t为何值时，与相似；求的面积S的最小值2022年山东省潍坊市潍城区中考一模数学试题一、单选题（本大题共8小题，共24分）1. 的平方根为（ )A. B. C. D. 【1题答案】【答案】C【解析】【分析】先按乘方法则计算，再根据平方根定义耱解即可【详解】解：(-4)2=16，16的平方根为4，的平方根为4，故选：C【点睛】本题考查平方根
10、，熟练掌握求一个数的平方根是解题的关键注意：一个正数的平方根有两个2. 我国古代数学家利用“牟合方盖”（如图甲）找到了球体体积的计算方法“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体，如图乙所示的几何体是可以形成“牟合方盖”的一种模型，它的左视图是（ ）A. B. C. D. 【2题答案】【答案】B【解析】【分析】根据左视图的定义，得出圆柱以及立方体的摆放即可得出左视图为2个正方形以及一个圆的组合体，进而得出答案即可【详解】解：利用圆柱直径等于立方体边长，得出此时摆放，圆柱左视图是正方形，得出圆柱以及正方体的摆放的左视图为1列，上边一个矩形，下边是正方形与
11、圆的组合体故选：B【点睛】此题主要考查了几何体的三视图；掌握左视图是从几何体左面看得到的平面图形是解决本题的关键3. 2021年，太原卫星发射中心发射了“羲和号”太阳双超卫星，拉开了太阳空间探测的序幕太阳是人类目前唯一可进行高时空分辨率和高光谱分辨率观测的恒星，它距地球约1.5亿公里，直径约139万公里，质量是地球的33万倍用科学计数法表示数据139万公里，并精确到十万位，则表示正确的为（ ）A. 公里B. 公里C. 公里D. 公里【3题答案】【答案】D【解析】【分析】科学记数法的表示形式为的形式，其中，n为整数确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数
12、相同当原数绝对值时，n是正数；当原数的绝对值时，n是负数【详解】解：139万公里=1390000公里公里，故选：D【点睛】此题考查科学记数法的表示方法科学记数法的表示形式为的形式，其中，n为整数，表示时关键要正确确定a的值以及n的值4. 将多项式因式分解，结果正确的是（ ）A. B. C. D. 【4题答案】【答案】B【解析】【分析】先运用完全平方公式展开，然后再合并，最后运用十字相乘法因式分解即可【详解】解：=故选B【点睛】本题主要考查了运用完全平方公式计算、十字相乘法因式分解等知识点，掌握运用十字相乘法进行因式分解是解答本题的关键5. 在中，P是射线上一动点，当时，的长为（ ）A. 4B.
13、 8C. 4或8D. 4或【5题答案】【答案】D【解析】【分析】分为点P在线段AC上时及点P在线段AC延长线上时两种情况进行讨论【详解】解：如图1，若点P在线段AC上时， 图1ABC=75，CBP=15，ABP=ABC-CBP=75-15=60，A=60，APB是等边三角形，BP=AB=4，如图2，若点P在线段AC延长线上时， 图2ABC=75，CBP=15，ABP=ABC+CBP=75+15=90，A=60，ABP=30，AP=2AB，综上所述，BP=4或，故选：D【点睛】本题考查了等边三角形的判定含30的直角三角形的性质，解决本题的关键是分类讨论解决问题6. 某数学兴趣小组做小球弹跳实验将
14、小球扔下，该小球反复地弹离地面，直到它停下下面的图象刻画了小球弹跳过程中球离地面的高度和时间之间的关系此过程中，小球有（ ）次距离地面0.45米A. 2B. 3C. 4D. 5【6题答案】【答案】B【解析】【分析】小球有几次距离地面的高度为0.45米，即图象中高度为0.45米的横线与图象的交点个数【详解】解：图象中高度为0.45米的横线与图象的交点个数为3个，所以小球有3次距离地面0.45米故选B【点睛】本题考查图象问题，准确理解题意并识图是解题的关键7. 等腰三角形边长分别为a，b，2，且a，b是关于x的一元二次方程的两个根，则n的值为（ ）A. 7B. 8C. 7或8D. 8或9【7题答案
15、】【答案】B【解析】【分析】由三角形是等腰三角形，得到a2，或b2，ab;当a2，或b2时，得到方程的根x2，把x2代入x26x+n+10即可得到结果；当ab时，方程x26x+n+10有两个相等的实数根，由（6）24（n+1）0可得结果【详解】解：三角形是等腰三角形，a2，或b2，ab两种情况，当a2，或b2时，a，b是关于x的一元二次方程x26x+n+10的两根，x2，把x2代入x26x+n+10得，2262+n+10，解得：n7，当n7，方程的两根是2和4，而2，4，2不能组成三角形，故n7不合题意，当ab时，方程x26x+n+10有两个相等的实数根，（6）24（n+1）0解得n8，当n8
16、，方程的根是3，则三角形的三边分别是2，3，3，符合题意，综上所述，n8，故选：B【点睛】本题考查了等腰直角三角形的性质，一元二次方程的根，一元二次方程根的判别式，注意分类讨论思想的应用8. “莱洛三角形”是机械学家莱洛研究发现的一种曲边三角形，转子发动机的设计就是利用了莱洛三角形它是分别以正三角形的顶点为圆心，以其边长为半径作弧形成的图形，如图2所示若正三角形的边长为3，则该“莱洛三角形”的面积为（ ）A. B. C. D. 【8题答案】【答案】A【解析】【分析】“莱洛三角形”的面积为三个以正三角形的两边和弧组成的扇形的面积减去重合的两次三角形的面积，根据扇形面积公式和等边三角形的面积求解即
17、可【详解】解：“莱洛三角形”是分别以正三角形的顶点为圆心，以其边长为半径作弧形成的图形，“莱洛三角形”的面积为三个以正三角形的两边和弧组成的扇形的面积减去重合的两次三角形的面积， ，故选：A【点睛】本题考查了扇形面积和等边三角形的面积，解题的关键是正确找出所求面积是由哪些特殊图形的面积构成的二、多选题（本大题共4小题，共12分）9. 下列调查中，适合用全面调查的是（ ）A. 调查黄河的水质情况B. 调查全国中学生的心理健康状况C. 调查某班级40名学生的视力情况D. 某客运公司检测10辆客运汽车的安全性能【9题答案】【答案】CD【解析】【分析】全面调查是指对总体中每个个体都进行的调查，一般适用
18、于总体中个体数量不太多的情况；抽样调查是指不必要或不可能对总体进行全面调查时，就从总体中抽取一部分个体进行调查，然后根据调查数据来推断总体的情况；根据全面调查与抽样调查的概念即可进行选择【详解】调查黄河水质及调查全国中学生的心理健康状况适合抽样调查，而调查某班级40名学生的视力情况、某客运公司检测10辆客运汽车的安全性能则适合用全面调查故选：CD【点睛】本题考查了统计调查的方法：抽样调查与全面调查，根据总体中个体的数量情况及是否具有破坏性、危险性来选择调查方法10. 关于x的分式方程解的情况，下列说法正确的是（ )A. 若，则此方程无解B. 若，则此方程无解C. 若方程的解为负数，则D. 若，
19、则方程的解为正数【10题答案】【答案】BC【解析】【分析】先按照一般步骤解方程，用含有a的代数式表示x，然后根据x的取值讨论a的范围，即可作出判断【详解】解：A、当a=0时，原分式方程为，解得：x=2，当x=2时，x-10，原分式方程的解为x=2，故本选项错误，不符合题意；B、，去分母得：，当a=1时，该方程无解，原分式方程无解；当a=-1时，原分式方程为，解得：x=1，当x=1时，x-1=0，x=1是增根，原分式方程无解；若，则此方程无解，故本选项正确，符合题意；C、，去分母得：，解得：，方程的解为负数，x0且x-10，且，解得：，故本选项正确，符合题意；D、若方程的解为正数，且，解得：且a
20、-1，当且a-1时，方程的解为正数，故本选项错误，不符合题意；故选：BC【点睛】考查了分式方程的解，解题关键是要掌握方程的解的定义，使方程成立的未知数的值叫做方程的解11. 如图，已知，点E，F分别在直线上，且平分平分，与相交于点O，则下列结论正确的是（ ）A. B. C. D. 【11题答案】【答案】AD【解析】【分析】由平分，得EFH=GFH，由ABCD可得EHF=GFH，再通过角平分线及等腰三角形三线合一性质可判定选项A；由得EHF=GFH，可判定选项B；由平行线的性质及等量代换可判定选项故选项D，从题目已知条件不能推出，故判定选项C【详解】解：平分，EFH=GFHABCD，EHF=GF
21、HEHF=EFHEF=EH，EG平分FEB，FEO=HEO，故选项A正确；，FOG=90，HFG+FGE=90，EHF=GFH，故选项B错误；EG平分FEB，FEO=HEOABCD，HEO=OGFFEO=FGOEF=FG，EF=EH，EH=FG，故选项D正确，从题目已知条件不能推出，故选项C错误，故选：AD【点睛】本题主要考查平行线的性质，等腰三角形的性质及判定，解题的关键是掌握等腰三角形三线合一性质等知识点12. 在同一平面直角坐标系中，如图所示，正比例函数与一次函数的图象则二次函数的图象可能是（ ）A. B. C. D. 【12题答案】【答案】BD【解析】【分析】根据正比例函数图象和一次函
22、数图象可得，然后分两种情况讨论：当时，；当时，即可求解【详解】解：根据题题得：当x=-1时，正比例函数与一次函数的图象相交，即， 当时，对于二次函数，当x=-1时，即，且，故B选项正确；当时，对于二次函数，当x=1时，即，且，故D选项正确；故选：BD【点睛】本题主要考查了一次函数的图象和性质，二次函数的图象和性质，熟练掌握一次函数的图象和性质，二次函数的图象和性质，利用分类讨论思想解答是解题的关键第卷 非选择题（共84分）三、填空题（本大题共4小题，共12分）13. 计算的结果是_【13题答案】【答案】1【解析】【分析】直接利用绝对值的性质、特殊角的三角函数值、负整数指数幂的性质分别化简得出答
23、案【详解】解：原式=1【点睛】此题主要考查了实数运算，正确化简各数是解题关键14. 云顶滑雪公园是北京2022年冬奥会7个雪上竞赛场馆中唯一利用现有雪场改造而成的下图左右两幅图分别是公园内云顶滑雪场U型池的实景图和示意图，该场地可以看作是从一个长方体中挖去了半个圆柱而成，它的横截面图中半圆的半径为，其边缘，点E在上，一名滑雪爱好者从点A滑到点E，他滑行的最短路线长为_m【14题答案】【答案】【解析】【分析】根据题意可得，AD12m，DECDCE24420m，线段AE即为滑行的最短路线长在R tADE中，根据勾股定理即可求出滑行的最短路线长【详解】解：如图，根据题意可知：AD12，DECDCE2
24、4420，线段AE即为滑行的最短路线长在TtADE中，根据勾股定理，得AE（m）故答案为：【点睛】本题考查了平面展开最短路径问题，解决本题的关键是掌握圆柱的侧面展开图是矩形，利用勾股定理求最短距离15. 如图是一张四边形纸片，点M，N分别是，上的点，将沿直线翻折，将沿直线翻折，点A和点B落在同一点G处，再将纸片沿直线折叠，点C恰好落在点D处，则的长为_【15题答案】【答案】17【解析】【分析】首先根据平行线的性质可得，再根据翻折的性质，可得，GD=8cm，设，则GN=acm，DN=(8+a)cm，再由折叠的性质可得，可求得，据此即可求得a的值，即可求得BC的长【详解】解： 沿直线翻折后得到，沿
25、直线翻折后得到 ， 设cm则cm 、G、N三点共线cm由对折知， 且 得，解得 故 故答案为：17【点睛】本题考查了平行线的性质，折叠的性质，相似三角形的判定与性质，熟练掌握和运用各图形的性质是解决本题的关键16. 如图，在平面直角坐标系中，点B的坐标为，轴，反比例函数的图象与交于点C，与交于点E，且，则点E的坐标为_【16题答案】【答案】【解析】【分析】由点B的坐标及，可求得AC的长，从而得BC的长，则可得点C、A的坐标，可求出反比例函数的解析式及直线OA的解析式，联立两个解析式并解方程组即可求得点E的坐标【详解】点B的坐标为 OB=4轴，即AC=10点C坐标为，点A的坐标为点C在反比例函数
26、的图象上直线OA过原点设直线OA的解析式为y=mx(m0)把点A的坐标代入上式得：即直线OA的解析式为联立反比例函数与一次函数解析式得：消去y并解得：，（舍去）则点E的坐标为故答案为：【点睛】本题是反比例函数与一次函数的综合，考查了求反比例函数与一次函数的解析式，反比例函数图象与一次函数图象的交点，由已知面积求得AC的长是解题的关键四、解答题（本大题共7小题，共72分）17. 先化简，再求值：，其中a为不等式组的整数解【17题答案】【答案】；当时，原式；当时，原式【解析】【分析】先将分子分母因式分解，再进行计算，然后解出不等式组，根据分式有意义的条件，可得a=0或1，即可求解【详解】解：由不等
27、式得，；由不等式得，；所以a为整数，a取，0，1，2，要使原分式有意义，则a不能为，2，当时，原式；当时，原式【点睛】本题主要考查了分式的化简求值，解一元一次不等式组，熟练掌握相关运算法则是解题的关键18. 某移动公司为了提升网络信号，在坡度的山坡上加装了信号塔（如图所示），信号塔底端Q到坡底A的距离为3.9米为了提醒市民，在距离斜坡底A点5.4米的水平地面上立了一块警示牌，当太阳光线与水平线所成的夹角为时，信号塔顶端P的影子落在警示牌上的点E处，且长为3米（1）求点Q到水平地面的铅直高度；（2）求信号塔的高度大约为多少米？（参考数据：）【18题答案】【答案】（1）1.5米 （2）13.2米【
28、解析】【分析】（1）作，根据坡度的定义设，在中，由勾股定理可得，代入求出QH的长；（2）作，在中，利用锐角三角函数关系得出PS的长，进而得出答案【小问1详解】解：作，垂足为H，由，可得，设，则，在中，由勾股定理可得，解得，（米），所以，点Q到水平地面的铅直高度是1.5米【小问2详解】解：作，垂足为S，则，在中，即（米），（米）所以，信号塔的高度大约为13.2米【点睛】此题考查了解直角三角形的应用坡度坡角问题，解决本题的关键是熟练掌握坡度坡角的概念20. 某商场为掌握国庆节期间顾客购买商品时刻的分布情况，统计了10月1日7:00-23:00这一时间段内5000名顾客的购买时刻顾客购买商品时刻的频
29、数分布直方图和扇形统计图如图所示，将7:00-23:00这一时间段划分为四个小的时间段：A段为，B段为，C段为，D段为，其中t为顾客购买商品的时刻，扇形统计图中，A，B，C，D四段各部分圆心角的度数比为1342请根据上述信息解答下列问题：（1）通过计算将频数直方图补充完整，并直接写出顾客购买商品时刻的中位数落在哪个时间段？（2）求10月1日这天顾客购买商品时刻的平均值（同一时间段内顾客购买商品时刻的平均值用该时段的中点值代表例如，A段的中点值为：）；（3）为活跃节日气氛，该商场设置购物后抽奖活动，设立了特等奖一个，一等奖两个，二等奖若干，并随机分配到A，B，C，D四个时间段中请直接写出特等奖出
30、现在A时间段的概率；请利用画树状图或列表的方法，求两个一等奖出现在不同时间段的概率【20题答案】【答案】（1）见解析， （2）15.8 （3）；画图见解析，【解析】【分析】（1）根据圆心角的比算出各部分的数量，补全频数分布直方图即可；按照时间段从早到晚进行排序，根据各部分的人数推断出排在中间第2500和2501名所在的时间段即可得出中位数所处的时间段；（2）按照加权平均数的计算公式计算即可；（3）直接根据概率公式进行计算即可；先画树状图，然后再利用概率公式进行计算即可【小问1详解】解：B段：，C段：补图：中位数落在C段：【小问2详解】，所以，该天顾客购买商品时刻的平均值为15.8【小问3详解】
31、特等奖出现在A时间段的概率为； （或列表法）共有16种等可能的结果，两个一等奖出现在不同时间段的情况有12种，两个一等奖出现在不同时间段的概率是【点睛】本题主要考查了频数分布直方图与扇形统计图结合，列表或画树状图求概率，根据题意画出树状图或列出表格是解题的关键22. 如图，以的边为直径的交于点F，点E是的中点，连接并延长交于点D，若（1）求证：是的切线；（2）若的半径为2，求的长【22题答案】【答案】（1）证明见解析 （2）6【解析】【分析】（1）连接，根据是的直径，得出，点E为弧的中点，得出，再根据，证明即可；（1）根据已知条件得出，即可得出AD=AB，根据AB=4，算出AC，即可得出CD长
32、度【小问1详解】证明：连接，如图所示：是的直径，点E为弧的中点，又，是的切线【小问2详解】解：，在中，即，得，【点睛】本题主要考查了圆周角定理、切线的证明、等腰三角形的判定和性质，解直角三角形，正确作出辅助线是解题的关键24. 某公司生产的一种产品在市场上很受欢迎，该公司每年的产量为6万件，可在国内和国外两个市场全部销售若在国外销售，平均每件产品的利润（元）与国外销售量x（万件）之间的函数关系如图所示若在国内销售，平均每件产品的利润为元，设该公司每年在国内和国外销售的总利润为w万元（1）求与x之间的函数表达式，并写出x的取值范围；（2）该公司每年在国内国外销售量各为多少时，可使公司每年的总利润
33、最大？最大总利润是多少？【24题答案】【答案】（1） （2）公司每年的国外销售量为4万件，国内销售量为2万件时，可使公司每年的总利润最大，最大总利润是580万元【解析】【分析】（1）分两种情况，用待定系数法可得答案；（2）结合（1）分别计算分段利润函数的最大值，最后得出最大值即可；【小问1详解】当时，当时，设，将，代入得：解得，此时，综上所述，【小问2详解】当时，；，当时，；当时，当时，当时，w取最大值580，答：当该公司每年的国外销售量为4万件，国内销售量为2万件时，可使公司每年的总利润最大，最大总利润是580万元【点睛】本题考查了二次函数在成本利润问题中的应用，前两问相对比较简单，第三问由
34、于含有两个变量，分析难度较大，总体来说，本题中等难度略大26. 如图，二次函数经过菱形的顶点A，B，D，且，点D的坐标为(0，4)，延长交抛物线于另一点E，连接，交于点F（1）求二次函数的表达式；（2）求的面积；（3）如图，直线l是二次函数图象的对称轴，若P为l上一点，且P，D，B三点构成以为底的等腰三角形，求点P的坐标【26题答案】【答案】（1） （2） （3）点P的坐标为【解析】【分析】（1）根据待定系数法代入点A、B、D的坐标求解即可；（2）根据求解即可；（3）根据题意，四边形是菱形，垂直平分，所以要使点P，D，B三点构成以为底的等腰三角形，须点P在对角线上，求出直线AC的解析式，再由P
35、在对称轴，可求解【小问1详解】解：点D的坐标为，四边形为菱形，在中，点A的坐标为，点B的坐标为又抛物线过点，可得解得：，【小问2详解】解：四边形为菱形，即轴，点E的纵坐标为4令，得得，点E的横坐标为，可得过点F作轴，交于M，交于N，则，又，【小问3详解】解：四边形是菱形，垂直平分，要使点P，D，B三点构成以为底的等腰三角形，则点P在对角线上设直线的表达式为，由点A的坐标为和点C的坐标为，可得，得直线表达式为由，可得对称轴为点P在抛物线的对称轴上，将代入，得点P的坐标为【点睛】本题考查了用待定系数法求二次函数的解析式，二次函数的性质，二次函数与三角形的面积问题，等腰三角形问题， 相似三角形的判定
36、与性质，解题的关键是综合运用二次函数与几何的性质解题28. 如图，矩形中，为等边三角形点E，F分别为边上的动点，且，P为上一动点，连接，将线段绕点B顺时针旋转至，连接（1）求证：；（2）当三条线段的和最小时，求的长；（3）若点E以每秒2个单位的速度由A点向D点运动，点P以每秒1个单位的速度由E点向F点运动E，P两点同时出发，点E到达点D时停止，点P到达点F时停止，设点P的运动时间为t秒求t为何值时，与相似；求的面积S的最小值【28题答案】【答案】（1）证明见解析 （2） （3）；【解析】【分析】（1）等边三角形的性质，可得，再由旋转的性质可得到，即可求证；（2）作，交于点，则，根据题意可得当G
37、，M，P，E四点共线时，最小，再由为等边三角形，可得，然后根据，可即可求解；（3）根据题意可得：，则再利用相似三角形的性质，即可求解；分两种情况讨论：当时，当时，即可求解小问1详解】证明：为等边三角形又；小问2详解】解：如图，作，交于点，则，为等边三角形，当G，M，P，E四点共线时，最小，为等边三角形，为等边三角形，当三条线段的和最小时，；【小问3详解】解：由题意得：，则，若，则，即（不合题意，舍去）；若，则需，即，解得；综上所述，当时，当时，所以当时，的面积最小为当时，故时，的面积最小为综上所述，的面积最小为【点睛】本题主要考查了图形的旋转，等边三角形的判定和性质，相似三角形的判定和性质，解直角三角三角形，熟练掌握图形的旋转的性质，等边三角形的判定和性质，相似三角形的判定和性质是解题的关键
