1、20222022 年年南京南京市中考考前猜题数学试卷市中考考前猜题数学试卷 一选择题（共一选择题（共 6 6 小题，满分小题，满分 1212 分，每小题分，每小题 2 2 分）分） 1下列计算结果为正数的是（ ） A|2| B（1）0 C （1）2 D32 2 某市在一次扶贫助残活动中， 捐款约 61800000 元， 请将 61800000 元用科学记数法表示， 其结果为 （ ） A0.618109 元 B6.18106元 C6.18107 元 D618105 元 3某校饭堂随机抽取了 100 名学生，对他们最喜欢的套餐种类进行问卷调查后（每人选一种） ，绘制了如图的条形统计图，根据图中的信
2、息，学生最喜欢的套餐种类是（ ） A套餐一 B套餐二 C套餐三 D套餐四 4已知 2m3，32n6，则下列关系成立的是（ ） Am+15n Bn2m Cm+1n D2m5+n 5已知关于x的分式方程3 的解是x3，则m的值为（ ） A3 B3 C1 D1 6如图，在边长为a的等边ABC中，分别取ABC三边的中点A1，B1，C1，得A1B1C1；再分别取A1B1C1三边的中点A2，B2，C2， 得A2B2C2； 这样依次下去， 经过第2021次操作后得A2021B2021C2021， 则A2021B2021C2021的面积为（ ） A B C D 第第卷（卷（非非选择题，共选择题，共 10810
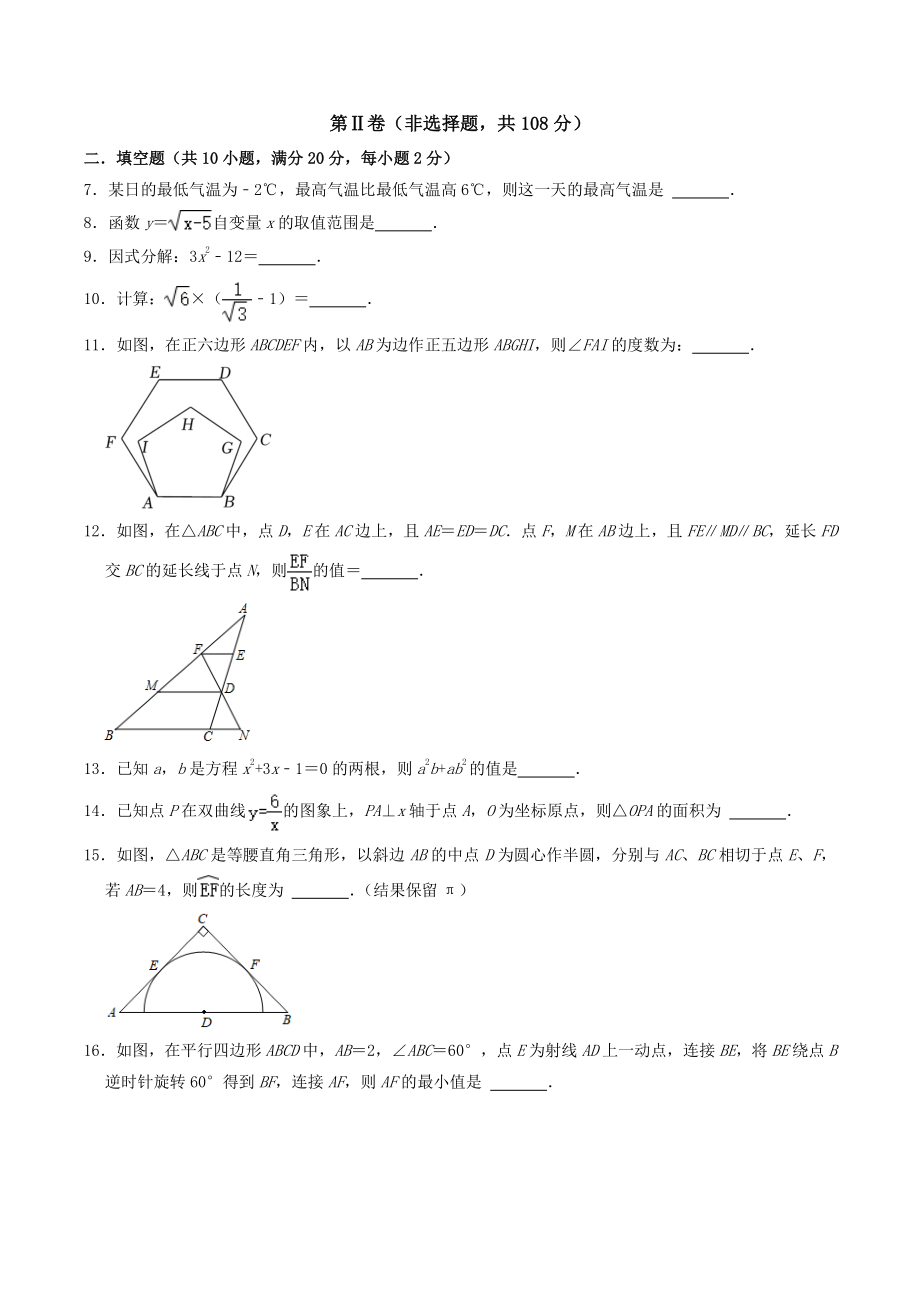
3、8 分）分） 二填空题（共二填空题（共 1010 小题，满分小题，满分 2020 分，每小题分，每小题 2 2 分）分） 7某日的最低气温为2，最高气温比最低气温高 6，则这一天的最高气温是 8函数y自变量x的取值范围是 9因式分解：3x212 10计算：（1） 11如图，在正六边形ABCDEF内，以AB为边作正五边形ABGHI，则FAI的度数为： 12如图，在ABC中，点D，E在AC边上，且AEEDDC点F，M在AB边上，且FEMDBC，延长FD交BC的延长线于点N，则的值 13已知a，b是方程x2+3x10 的两根，则a2b+ab2的值是 14已知点P在双曲线的图象上，PAx轴于点A，O为
4、坐标原点，则OPA的面积为 15如图，ABC是等腰直角三角形，以斜边AB的中点D为圆心作半圆，分别与AC、BC相切于点E、F，若AB4，则的长度为 （结果保留 ） 16如图，在平行四边形ABCD中，AB2，ABC60，点E为射线AD上一动点，连接BE，将BE绕点B逆时针旋转 60得到BF，连接AF，则AF的最小值是 三解答题（共三解答题（共 1111 小题，满分小题，满分 8888 分）分） 17 （7 分）计算：6sin45|1|（2021）0（）2 18 （7 分）先化简、再求值：，其中x 19 （8 分）解不等式组： 20 （8 分）某校合唱团为了开展线上“百人合唱一首歌”的“云演出”活
5、动，需招收新成员小贤、小晴、小艺、小志四名同学报名参加了应聘活动，其中小贤、小艺来自七年级，小志、小晴来自八年级现对这四名同学采取随机抽取的方式进行线上面试 （1）若随机抽取一名同学，恰好抽到小艺同学的概率为 ； （2）若随机抽取两名同学，请用列表法或树状图法求两名同学均来自八年级的概率 21 （8 分）如图 1 是一间安装有壁挂式空调的卧室的一部分，如图 2 是该空调挂机的侧面示意图已知空调挂机底部BC垂直于墙面CD，且当导风板所在的直线AE与竖直直线AB的夹角 为 42时， 空调风刚好吹到床的外边沿E处，CDED于点D，ABED于点F若AB0.02m，BC0.2m，床铺ED2.4m，求空调
6、机的底部位置距离床的高度CD （结果精确到 0.1m，参考数据：sin420.67，cos420.74，tan420.90） 22 （8 分）如图，已知 RtABC，B90 （1）作O，使得圆心O在线段AC上，O经过点C，且与AB相切于点D； （2）若AD3，O的半径为 4，求BC的长 23 （8 分）如图，D，E为GCF中GF边上两点，过D作ABCF交CE的延长线于点A，AECE （1）求证：ADECFE； （2）若GB4，BC6，BD2，求AB的长 24 （8 分）2020 年，新型冠状病毒肆虐，给人们的生活带来许多不便，网络销售成为这个时期最重要的一种销售方式某乡镇农贸公司新开设了一家网
7、店，销售当地农产品其中一种当地特产在网上试销售，其成本为每千克 2 元公司在试销售期间，调查发现，每天销售量y（kg）与销售单价x（元）满足如图所示的函数关系（其中 2x10） （1）求y与x之间的函数关系式； （2）销售单价x为多少元时，每天的销售利润最大？最大利润是多少元？ 25 （8 分）垃圾的分类回收不仅能够减少环境污染、美化家园，甚至能够变废为宝、节约资源为增强学生垃圾分类意识，推动垃圾分类进校园，某中学组织全校 1565 名学生参加了“垃圾分类知识竞赛”（满分为 100 分） 该校数学兴趣小组为了解全校学生竞赛分数情况，采用简单随机抽样的方法（即每名学生的竞赛分数被抽到的可能性相等
8、的抽样方法）抽取部分学生的竞赛分数进行调查分析 （1）以下三种抽样调查方案： 方案一：从七年级、八年级、九年级中指定部分学生的竞赛分数作为样本； 方案二：从七年级、八年级中随机抽取部分男生的竞赛分数以及在九年级中随机抽取部分女生的竞赛分数作为样本； 方案三：从全校 1565 名学生的竞赛分数中随机抽取部分学生的竞赛分数作为样本 其中抽取的样本最具有代表性和广泛性的一种抽样调查方案是 （填写“方案一”、“方案二”或“方案三”） ； （2） 该校数学兴趣小组根据简单随机抽样方法获得的样本， 绘制出如下统计表 （90 分及以上为“优秀”，60 分及以上为“及格”，学生竞赛分数记为x分） 样本容量 平
9、均分 及格率 优秀率 最高分 最低分 100 83.59 95% 40% 100 52 分数段 50 x60 60 x70 70 x80 80 x90 90 x100 频数 5 7 18 30 40 结合上述信息解答下列问题： 样本数据的中位数所在分数段为 ； 全校 1565 名学生，估计竞赛分数达到“优秀”的学生有 人 26 （9 分）如图，抛物线yx2+bx+c分别与x轴交于点A，B，与y轴交于点C，点B（1，0） ，且OC4OB，点P（m，0）为线段OA上（不含端点）的动点，过点P作x轴的垂线交抛物线于点Q，连接AC，交PQ于点M （1）求抛物线的函数解析式； （2）当点M分线段PQ的比
10、为 1：2 时，求m的值 27 （9 分）问题提出 （1）如图，在等腰 RtABC中，ACB90，D是AB边上一点，以CD为腰作等腰 RtCDE，连接BE，则AD与BE的数量关系是 ，位置关系是 ； 问题探究 （2）如图，AB是半圆O的直径，C、D是半圆O上两点，且ACBC，若BD3，AD9，求CD的长； 问题解决 （3）如图是某公园的一个面积为 36m2的圆形广场示意图，点O为圆心，公园开发部门计划在该广场内设计一个四边形运动区域ABDC， 连接BC、AD， 其中等边ABC为球类运动区域， BCD为散步区域，设AD的长为x，BDC的面积为S 求S与x之间的函数关系式； 按照设计要求，发现当点
11、D为的中点时，布局设计最佳，求此时四边形运动区域ABDC的面积 参考答案参考答案 一选择题（共一选择题（共 6 6 小题，满分小题，满分 1212 分，每小题分，每小题 2 2 分）分） 1 2 3 4 5 6 C C B A A D 1 【解答】【解答】解：A、|2|20，结果为负数，故此选项不符合题意； B、（1）010，结果为负数，故此选项不符合题意； C、 （1）210，结果为正数，故此选项符合题意； D、3290，结果为负数，故此选项不符合题意； 故选：C 2 【解答】【解答】解：618000006.18107， 故选：C 3 【解答】【解答】解：根据条形统计图可知：学生最喜欢的套餐
12、种类是套餐一， 故选：A 4 【解答】【解答】解：32n6， 25n32， 2m3， 25n2m2， 则 25n2m+1， 5nm+1， 故选：A 5 【解答】【解答】解：把x3 代入分式方程3，得， 整理得 6+m3， 解得m3 故选：B 6 【解答】【解答】解：点A1，B1分别为BC，AC的中点， AB2A1B1， 点A2，B2分别为B1C1，A2C2的中点， A1B12A2B2， A2B2（）2a， AnBn（）na， A2021B2021（）2021a A2021B2021C2021的面积（）2021a2， 故选：D 二填空题（共二填空题（共 1010 小题，满分小题，满分 2020
13、分，每小题分，每小题 2 2 分）分） 7 【解答】【解答】解：2+64（） ， 故答案为：4 8 【解答】【解答】解：根据题意得，x50， 解得x5 故答案为：x5 9 【解答】【解答】解：原式3（x24） 3（x+2） （x2） 故答案为：3（x+2） （x2） 10 【解答】【解答】解：原式 故答案为 11 【解答】【解答】解：在正六边形ABCDEF内，正五边形ABGHI中，FAB120，IAB108， FAIFABIAB12010812， 故答案为：12 12 【解答】【解答】解：EFDMBC，AEDECD， ， 在EFD与CND中， ， EFDCND（AAS） ， EFCN， CN：
14、BC1：3， CN：BN1：4， ， 故答案为 13 【解答】【解答】解：a，b是方程x2+3x10 的两根， 根据根与系数的关系得：a+b3，ab1， a2b+ab2ab（a+b）（1）（3）3， 故答案为：3 14 【解答】【解答】解：P在双曲线的图象上，PAx轴于点A， SOPA3 故答案为：3 15 【解答】【解答】解：连接OE、OF， AB4，点D为AB的中点， AD2， AC、BC是半圆的切线， DEAC，DFBC， C90， EDF90， ABC为等腰直角三角形， A45， DEAD， 的长， 故答案为： 16 【解答】【解答】解：如图，以AB为边向下作等边ABK，连接EK，在E
15、K上取一点T，使得ATTK BEBF，BKBA，EBFABK60， ABFKBE， ABFKBE（SAS） ， AFEK， 根据垂线段最短可知，当KEAD时，KE的值最小， 四边形ABCD是平行四边形， ADBC， ABC60， BAD180ABC120， BAK60， EAK60， AEK90， AKE30， TATK， TAKAKT30， ATETAK+AKT60， ABAK2， AEAK1， EKAE， AF的最小值为 故答案为： 三解答题（共三解答题（共 1111 小题，满分小题，满分 8888 分）分） 17 【解答】【解答】解：原式6（1）214 3+124 3 18 【解答】【解
16、答】解：原式 ， 当时， 原式 19 【解答】【解答】解：， 由得x3， 由得x1， 所以，原不等式组得解集为1x3 20 【解答】【解答】解： （1）共有 4 种可能出现的结果，抽到小艺的只有 1 种， 因此恰好抽到小艺的概率为， 故答案为：； （2）用列表法表示所有可能出现的结果如下： 共有 12 种可能出现的结果，其中都是八年级，即抽到小志、小晴的有 2 种， P（小志、小晴） 21 【解答】【解答】解：由题知，四边形BCDF是矩形， BC0.2m，ED2.4m， EFEDFDEDBC2.40.22.2（m） ， EAF42，tanEAF， AF2.44（m） ， CDBFAFAB2.4
17、40.022.4（m） ， 答：空调机的底部位置距离床的高度CD长约为 2.4m 22 【解答】【解答】解： （1）如图，O即为所求作 （2）AB是O的切线， ODAB， ADO90， AD3，ODOC4， OA5， ACAO+OC5+49， ADOB90， ODBC， ， ， BC 23 【解答】【解答】 （1）证明：ABCF， AECF， 在ADE和CFE中， ， ADECFE（ASA） ； （2）解：DBCF， GBDGCF， ， GB4，BC6，BD2， GCGB+BC10， ， CF5， ADECFE， ADCF5， ABAD+BD5+27 24 【解答】【解答】解： （1）当 2x
18、5 时，y600； 当 5x10 时，设ykx+b（k0） ，把（5，600） ， （10，400）代入得： ， 解得， y40 x+800， y与x之间的函数关系式为： y； （2）设每天的销售利润为w元， 当 2x5 时， w600（x2）600 x1200， 当x5 时，wmax600512001800（元） ； 当 5x10 时， w（40 x+800） （x2） 40（x11）2+3240， 当x10 时， wmax401+32403200（元） 综上所述，销售单价x为 10 元时，每天的销售利润最大，最大利润是 3200 元 25 【解答】【解答】解： （1）根据抽样的代表性、普遍
19、性和可操作性可得，方案三：从全校 1565 名学生的竞赛分数中随机抽取部分学生的竞赛分数作为样本进行调查分析，是最符合题意的 故答案为：方案三； （2）样本总数为：5+7+18+30+40100（人） ， 成绩从小到大排列后，处在中间位置的两个数都在 80 x90，因此中位数在 80 x90 组中； 由题意得，1565626（人） ， 故答案为：80 x90；626 26 【解答】【解答】解： （1）B（1，0） ， OB1， OC4OB4， C（0，4） ， 将B（1，0） ，C（0，4） ，代入yx2+bx+c得：b3，c4， 抛物线的函数解析式为yx23x4； （2）令y0，则有x23x
20、40， 解得：x11，x24， B（1，0） ，A（4，0） ， 直线AC的解析式为：yx4， P（m，0） ， M（m，m4） ，Q（m，m23m4） ， PM（m4） ，PQ（m23m4） ， 当点M分线段PQ的比为 1：2 时，分两种情况： 当PM：MQ1：2 时，则PM：PQ1：3，即， 解得：m12，m24（与A点重合，舍去） ， 当PM：MQ2：1 时，则PM：PQ2：3，即， 解得：m1，m24（与A点重合，舍去） ， 故当点M分线段PQ的比例为 1：2 时，m的值为 2 或 27 【解答】【解答】解： （1）等腰 RtABC中，ACB90， ACB90，ACBA45， CDE是
21、等腰直角三角形， DCEACB90， ACD90DCBBCE， ACBC，DCEC， ACDBCE（SAS） ， ADBE，CBEA45， DBEABC+CBE90， ADBE， 故答案为：相等，垂直； （2）过点C作CECD交AD于点E，如图： AB是半圆O的直径， ABC90， ABAC， ABC45， ADC45， CECD， ACE90ECBBCD，DCE是等腰直角三角形， CAECBD，ACBC， ACEBCD（ASA） ， AEBD3， DEADAE936， 在等腰 RtDCE中，CDDE3； （3）在DA上截取DECD，连接CE，过点C作CFAD于点F，过O作OHAB于H，如图：
22、 ABC是等边三角形， ABC60ADC，CECD， DECD， CDE是等边三角形， O的面积为 36， O的半径为 6，即OA6， ABC是等边三角形，OHAB AB2AH，AOH60， 在 RtAOH中，AHOAsinAOH3， AB6ACBC， ABC、CDE是等边三角形， ACBDCE60，CECD，ACBC， ACE60ECBBCD， BCDACE（SAS） ， SBCDSACE， 设CD2a，则EFDFa，CFa， 而ADx， RtACF中，AC2CF2+AF2， （6）2（a）2+（xa）2， 化简变形得：ax2a2x254， SSACEAECF （x2a）a （ax2a2） x227； D为BC的中点时，如图： CDE是等边三角形， CDE60， D为BC的中点， CADCAB30， ACD90， AD是O的直径， CDDEADOD， 点E与点O重合， SSACESAOCSABC， S四边形ABDCS+SABCSABCAB236
