 2022年江苏省泰州市中考仿真数学试卷(含答案解析)
2022年江苏省泰州市中考仿真数学试卷(含答案解析)
《2022年江苏省泰州市中考仿真数学试卷(含答案解析)》由会员分享,可在线阅读,更多相关《2022年江苏省泰州市中考仿真数学试卷(含答案解析)(26页珍藏版)》请在七七文库上搜索。
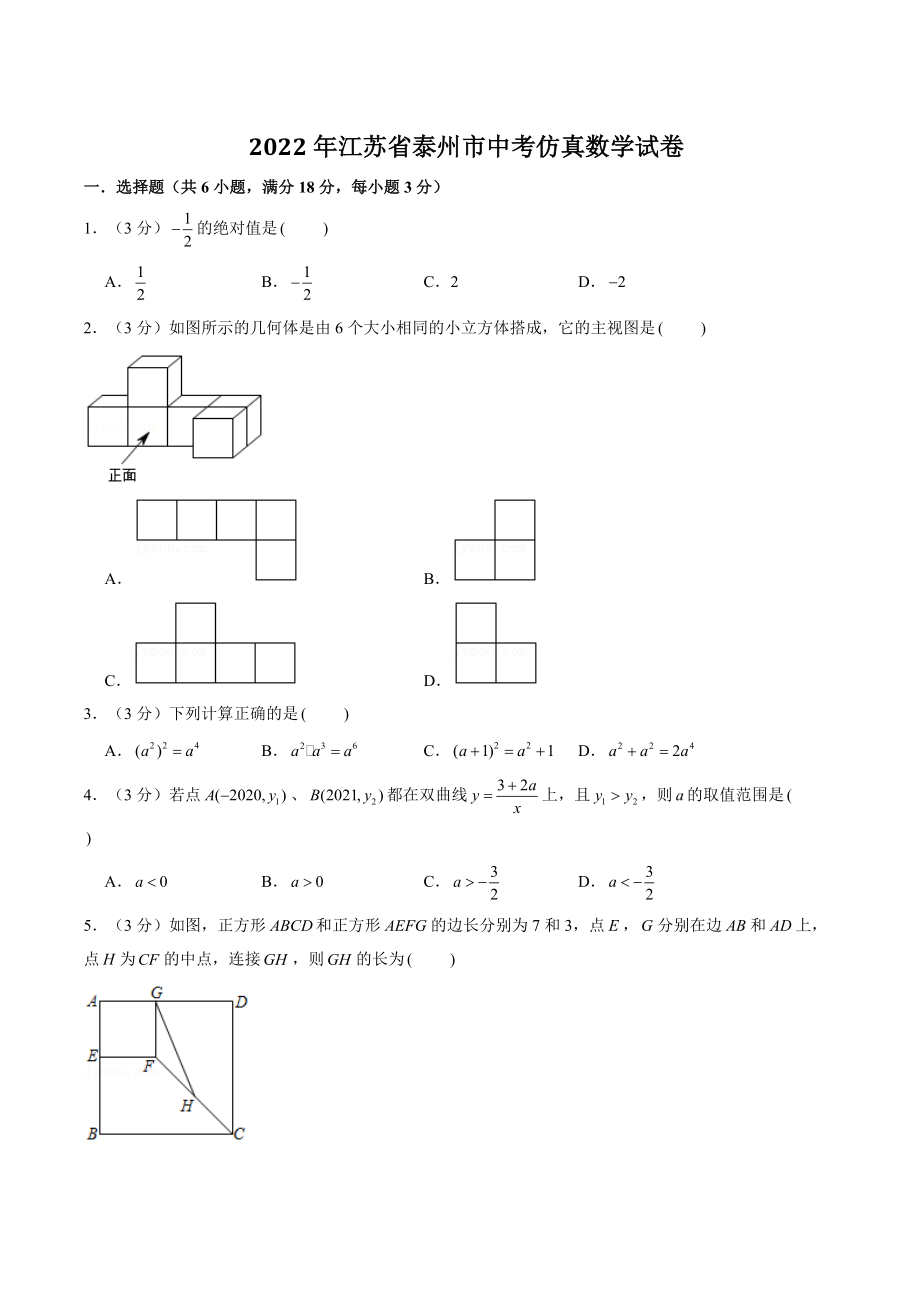
1、 2022年江苏省泰州市中考仿真数学试卷一选择题(共6小题,满分18分,每小题3分)1(3分)的绝对值是ABC2D2(3分)如图所示的几何体是由6个大小相同的小立方体搭成,它的主视图是ABCD3(3分)下列计算正确的是ABCD4(3分)若点、都在双曲线上,且,则的取值范围是ABCD5(3分)如图,正方形和正方形的边长分别为7和3,点,分别在边和上,点为的中点,连接,则的长为ABCD56(3分)对于二次函数,若时随着的增大而增大,则符合条件的整数的值不可能为A3B4C5D6二填空题(共10小题,满分30分,每小题3分)7(3分)在函数中,自变量的取值范围是8(3分)我国高铁通车总里程居世界第一,
2、到2020年末,高铁总里程达到37900千米,37900用科学记数法表示为9(3分)已知,则 10(3分)如图,以正五边形的边为斜边,在五边形内作等腰直角,且,则的大小是 11(3分)某中学为了选拔一名运动员参加市运会100米短跑比赛,有甲、乙两名运动员备选,他们最近测试的10次百米跑平均时间都是12.83秒,他们的方差分别是(秒,(秒,如果要选择一名成绩优秀且稳定的人去参赛,应派 去12(3分)若一次函数的图象与反比例函数的图象相交于点,、,则的值为13(3分)如图,圆锥的底面半径为,侧面积为,设圆锥的母线与高的夹角为,则的值为14(3分)如图,的半径为,四边形内接于,则的值为15(3分)如
3、图,在边长为1的小正方形网格中,若和的顶点都在小正方形网格的格点上,则16(3分)如图,在平面直角坐标系中,四边形是矩形,点、分别在轴、轴的正半轴上,点的坐标为,若点是第一象限内的一点,且,则线段最长时的点坐标为 三解答题(共10小题,满分102分)17(12分)(1)计算:;(2)解不等式组,并写出不等式组的正整数解18(8分)为了增强学生的疫情防控意识,响应“停课不停学”号召,某学校组织了一次“疫情防控知识专题网上学习并进行了一次全校2500名学生都参加的网上测试,阅卷后,教务处随机抽取收了100份答卷进行分析统计,发现考试成绩分)的最低分为51分,最高分为满分100分,并绘制了尚不完整的
4、统计图表,请根据图表提供的信息,解答下列问题:分数段(分频数(人频率0.1180.18350.35120.12合计1001(1)填空:,;(2)将频数分布直方图补充完整;(3)在绘制扇形统计图中,这一分数段所占的圆心角度数为 ;(4)该校对成绩为的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为,请你估算全校获得二等奖的学生人数19(8分)2021年9月30日,以抗美援朝战争中长津湖战役为背景的电影长津湖在各大影院上映后,嬴得口碑与票房双丰收小亮和小明都想去观看这部电影,但是只有一张电影票,于是他们决定采用摸球的办法决定胜负,获胜者去看电影,游戏规则如下:在一个
5、不透明的袋子中装有编号为1,2,3,4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后不放回,再从中摸出一个球,记下数字,若两次数字之和大于5,则小亮获胜,若两次数字之和小于5,则小明获胜请用列表或画树状图的方法求小明获胜的概率20(8分)如图,已知,在中,(1)在线段找一点,使得点到边的距离等于的长(用尺规作图,保留作图痕迹,不要求写作法);(2)在(1)的条件下,求的长21(10分)去年某商店“十一黄金周”进行促销活动期间,前六天的总营业额为450万元,第七天的营业额是前六天总营业额的(1)求该商店去年“十一黄金周”这七天的总营业额;(2)去年,该商店7月份的营业额为350万元,
6、8、9月份营业额的月增长率相同,“十一黄金周”这七天的总营业额与9月份的营业额相等求该商店去年8、9月份营业额的月增长率22(10分)中国溱潼会船节,属于国家级非物质文化遗产,被誉为“民俗文化之大观,水乡风情之博览”,撑篙子船是会船节活动中最具有特色的比赛项目某篙子手发现篙子刚开始触及到河床的点时,篙子与水面所成的角,紧握篙子的右手处离水面的高度为2米俯身发力后,篙子与水面所成的角,此时紧握篙子的右手处离水面的高度为1米,整个过程右手与篙,篙与河床均无滑动,河床近似地看作与水面平行,求此处水面离河床的高度是多少米?(结果精确到0.01米,23(10分)如图,点、在反比例函数的图象上,轴,轴,垂
7、足分别为、,与相交于点(1)根据图象直接写出、的大小关系,并通过计算加以验证;(2)结合以上信息,从四边形的面积为2,这两个条件中任选一个作为补充条件,求的值你选择的条件是 (只填序号)24(10分)如图,中,点在边上,以为直径的与直线相切于点,且是的中点,连接(1)求和的度数;(2)如图,连接,若,求的半径25(12分)阅读理解:对于线段和点,定义:若,则称点为线段的“等距点”;特别地,若,则称点是线段的“完美等距点”解决问题:如图,在平面直角坐标系中,为坐标原点,点的坐标为,点是直线上一动点(1)已知4个点:、,则线段的“等距点”是,线段的“完美等距点”是(2)若,点在轴上,且是线段的“等
8、距点”,求点的坐标;(3)当,是否存在这样的点,使点是线段的“等距点”且为线段的“完美等距点”,若存在,求出点的坐标;若不存在,说明理由26(14分)如图1,边长为1的正方形被两条与边平行的线段、分割成两个小矩形,与交于点,的周长为(1)若,求矩形的面积;(2)当满足什么条件时,矩形的面积是一个与满足条件的点、位置无关的常数?(3)在图2中作出符合(2)中要求的其中一个2022年江苏省泰州市中考仿真数学试卷一选择题(共6小题,满分18分,每小题3分)1(3分)的绝对值是ABC2D【答案】【详解】的绝对值是故选:2(3分)如图所示的几何体是由6个大小相同的小立方体搭成,它的主视图是ABCD【答案
9、】【详解】解:从正面看,共有四列,从左到右每列的正方形的个数分别为:1、2、1、1,故选:3(3分)下列计算正确的是ABCD【答案】【详解】、,正确;、,错误;、,错误;、,错误;故选:4(3分)若点、都在双曲线上,且,则的取值范围是ABCD【答案】【详解】点,两点在双曲线上,且,的取值范围是,故选:5(3分)如图,正方形和正方形的边长分别为7和3,点,分别在边和上,点为的中点,连接,则的长为ABCD5【答案】【详解】如图,延长交的延长线于,正方形和正方形的边长分别为7和3,点是的中点,在和中,故选:6(3分)对于二次函数,若时随着的增大而增大,则符合条件的整数的值不可能为A3B4C5D6【答


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2022 江苏省 泰州市 中考 仿真 数学试卷 答案 解析
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
文档标签
- 数学试卷
- 2022年山东省菏泽市中考仿真数学试卷含答案解析
- 2022年山东省德州市中考仿真数学试卷含答案解析
- 2022年江苏省徐州市中考仿真数学试卷2含答案解析
- 2022年山东省济宁市中考仿真数学试卷含答案解析
- 2022年江苏省徐州市中考仿真数学试卷1含答案解析
- 2022年湖北省襄阳市中考仿真数学试卷含答案解析
- 2022年湖北省岳阳市中考仿真数学试卷含答案解析
- 2022年湖南省永州市中考仿真数学试卷含答案解析
- 江苏2022年数学
- 2022年江苏省苏州市中考模拟仿真数学试卷含答案解析
- 2022年江苏省泰州市海陵区中考二模数学试卷含答案
- 2022年江苏省泰州市靖江市中考二模数学试卷含答案解析
- 2022年江苏省泰州市中考数学试卷含答案解析
- 2022年江苏省泰州市中考历史试卷含答案解析
- 2022年江苏省泰州市中考英语试卷含答案解析
- 2022年江苏省常州市中考仿真数学试卷1含答案解析
- 2022年江苏省泰州市中考数学试卷
- 泰州数学



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-211503.html