1、2022 年安徽省马鞍山市和县中考第一次模拟监测数学试题年安徽省马鞍山市和县中考第一次模拟监测数学试题 一、选择题（共 10 小题，满分 40 分） 1.在四个数 0，2，3，2 中，最小的数是（ ） A.0 B.2 C.3 D.2 2.下列计算正确的是（ ） A.3332bbb B.1644xxx C.224236aaa D.2510aa 3.北京冬奥会和冬残奥会赛会志愿者招募工作进展顺利，截止 2020 年底，赛会志愿者申请人数已突破 960000人.将 960000 用科学记数法表示为（ ） A.496 10 B.59.6 10 C.49.6 10 D.69.6 10 4.下列几何体中，
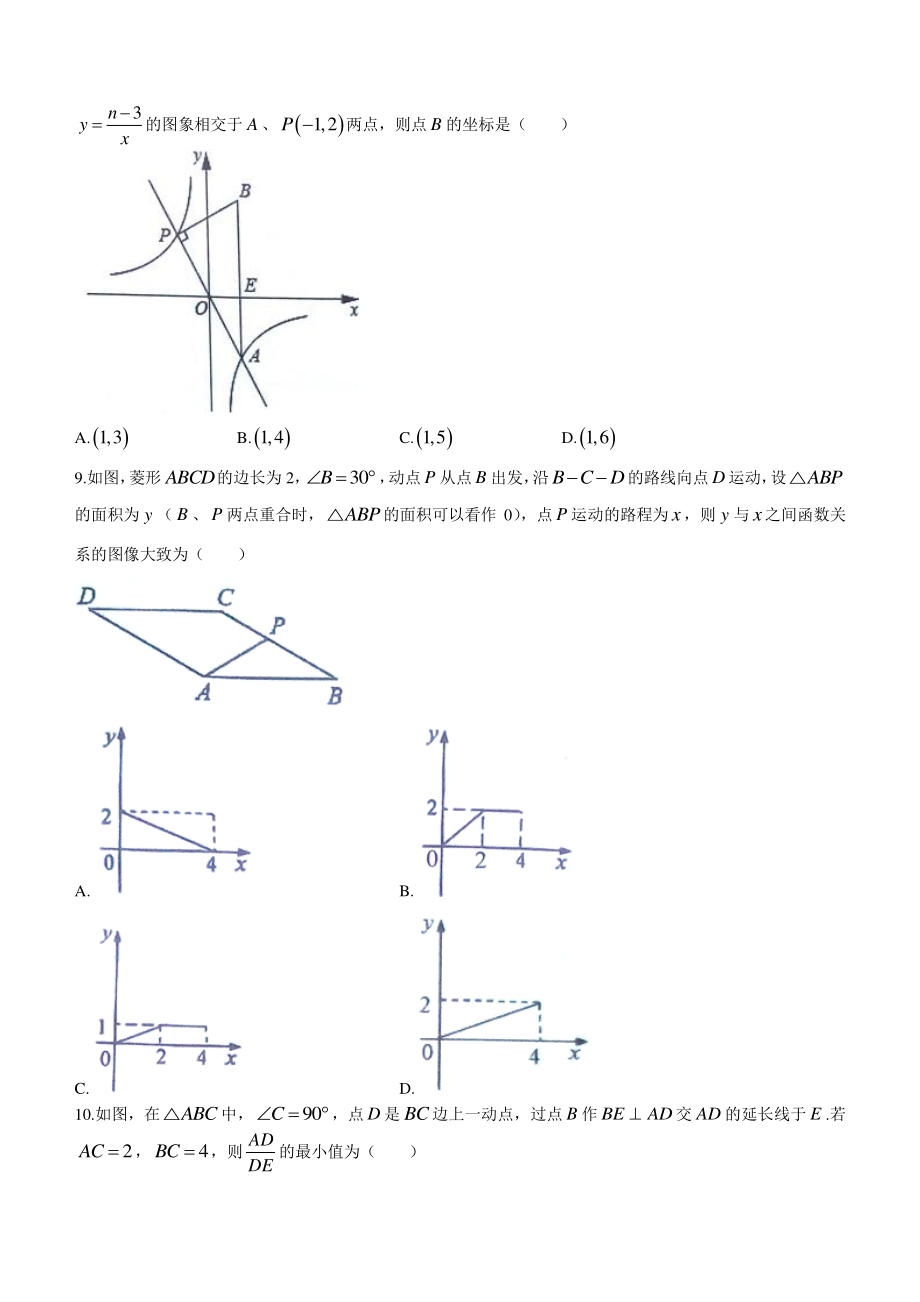
2、主视图是圆的是（ ） A. B. C. D. 5.化简211xxxx的结果是（ ） A.1x B.1x C.x D.x 6.不等式组20321xx 的解集是（ ） A.12x B.21x C.1x或2x D.21x 7.如图，:3:1AG GD，:2:3BD DC ，则:AE EC的值是（ ） A.8:7 B.6:5 C.3:2 D.8:5 8.如图，在平面直角坐标系中，PBPA，ABx轴于点E，正比例函数ymx的图象和反比例函数3nyx的图象相交于A、1,2P 两点，则点B的坐标是（ ） A.1,3 B.1,4 C.1,5 D.1,6 9.如图， 菱形ABCD的边长为 2，30B ， 动点P
3、从点B出发， 沿B CD的路线向点D运动， 设ABP的面积为y（B、P两点重合时，ABP的面积可以看作 0） ，点P运动的路程为x，则y与x之间函数关系的图像大致为（ ） A. B. C. D. 10.如图，在ABC中，90C，点D是BC边上一动点，过点B作BEAD交AD的延长线于E.若2AC ，4BC ，则ADDE的最小值为（ ） A.512 B.1 C.52 D.512 第卷（非选择题） 二、填空题（共 4 小题，满分 20 分，每小题 5 分） 11.若7mn，且m，n为两个连续的整数，则mn的值为_. 12.因式分解：29aba_. 13.为了在校运会中取得更好的成绩，小丁积极训练，在
4、某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是 1.68 米，当铅球运行的水平距离为 2 米时，达到最大高度 2 米的B处，则小丁此次投掷的成绩是_米. 14.如图，Q是ABC内一点，且满足QABQBCQCA. （1）如图 1，当ABC是等边三角形时，_； （2）如图 2，当ABC是等腰直角三角形（其中90ACB）时，QAC，QBA，QCB的面积之比是_. 三、解答题（共 2 小题，满分 16 分，每小题 8 分） 15.（8 分）计算：101351220224sin603 . 16.（8 分）我国北魏数学家张丘建的著作张丘建算经对于不定方程的典型问题有
5、独到见解，其中记载了这样一个问题，原文是： “今甲乙怀银，不知其数，乙得甲十银，适等，甲得乙十银，多乙余钱五倍，问甲乙各怀银几何？”译文为：现有甲、乙两人，带有一些银子，都不知道数量，甲给乙的 10 两银子，两人的银子恰好相等；乙给甲的 10 两银子，甲比乙多出的银子是乙的 5 倍，问甲、乙各带了多少两银子？请解答上述问题. 四、解答题（共 2 小题，满分 16 分，每小题 8 分） 17.（8 分）如图，ABC的顶点坐标分别为1, 1A ，3, 3B ，0, 3C. （1）画出ABC绕点C顺时针旋转 90得到的11ABC，并写出1B的坐标； （2）以点O为位似中心，将ABC放大为原来的 2
6、倍，得到222A B C，请在网格中画出222A B C. 18.（8 分）观察以下等式： 第 1 个等式：12112311，第 2 个等式：32112422， 第 3 个等式：52112533，第 4 个等式：72112644. 第 5 个等式：92112755. 按照以上规律，解决下列问题： （1）写出第 6 个等式：_； （2）写出你猜想的第n个等式：_（用含n的等式表示） ，并证明. 五、解答题（共 2 小题，满分 20 分，每小题 10 分） 19.如图，斜立于地面的木杆AB，从点C处折断后，上半部分BC倒在地上，杆的顶部B恰好接触到地面D处，测得60ACD，37ADC，杆的底部A与
7、点D相距 5 米，求木杆AB的长度.（精确到 0.1 米；参考数据：sin370.6，cos370.8，tan370.75，31.73） 20.如图，AB为O的直径，C是O上的一点，连接AC，BC，D是BC的中点，过D作DEAB于点E，交BC于点F. （1）求证：2BCDE； （2）若6AC ，10AB，求DF的长. 六、解答题（共 1 小题，满分 12 分） 21.某校体育组为了解全校学生“最喜欢的一项球类项目” ，随机抽取了部分学生进行调查，下面是根据调查结果绘制的不完整的统计图.请你根据统计图回答下列问题： 图 1 图 2 （1）本次调查的学生共有_人，扇形统计图中喜欢乒乓球的学生所占的
8、百分比为_； （2）请补全条形统计图（图 2） ，并估计全校 500 名学生中最喜欢“足球”项目的有多少人？ （3） 篮球教练在制定训练计划前， 将从最喜欢篮球项目的甲、乙、丙、 丁四名同学中任选两人进行个别座谈，请用列表法或树状图法求抽取的两人恰好是甲和乙的概率. 七、解答题（共 1 小题，满分 12 分） 22.在平面直角坐标系中，点O为坐标原点，设抛物线224yxbx的顶点为A.直线0ykx k与抛物线224yxbx交于A，B两点OAOB. （1）求k，b的值； （2）若点P在线段OB上任意一点，过P作x轴的垂线，垂足为C，PC的延长线交抛物线224yxbx于点D，求线段PD OC的最大
9、值. 八、解答题（共 1 小题，满分 14 分） 23.已知：ABC和ADE按如图所示方式放置， 点D在ABC内， 连接BD、CD和CE， 且90DCE. 图 图 图 （1）如图，当ABC和ADE均为等边三角形时，试确定AD、BD、CD三条线段的关系，并说明理由； （2）如图，当2BABCAC，2DADEAE时，试确定AD、BD、CD三条线段的关系，并说明理由： （3）如图，当:AB BC ACAD DE AEm n p时，请直接写出AD、BD、CD三条线段的关系. 参考答案参考答案 一、选择题（共 10 小题） 1C2D3B4C5D6A7B 8A 解：AP 为正比例函数，故点 A、P 关于原
10、点对称，则点 A（1，2） ，则设点 B（1，t） ， 过点 P 作 y 轴的平行线交 x 轴于点 N，交点 B 与 x 轴的平行线于点 M， MPB+NPO90，MPB+MBP90， NPOMPB， BM1（1）2PN2，PNOBMP90， PNOBMP（AAS） ， MPON1， 故 MNMP+PN1+23， 故点 B 的坐标为（1，3） ， 故选：A 9C 解：由题意知，点 P 从点 B 出发，沿 BCD 向终点 D 匀速运动，则 当 0 x2，y=12x， 当 2x4，y=1， 由以上分析可知，这个分段函数的图象是 C 故选 C 10D 分析：如图 1，过点 E 作 EFBC 于 F，
11、 C90， ACEF， ACDEDF， ADACDEEF， AEBE， A，B，E，C 四点共圆， 设 AB 的中点为 O，连接 OE， 如图 2，当点 E 是BC中点时，EF 的值最大，此时 E，F，O 共线 AC2，BC4， 2222242 5ABACBC， 5OEOB， OEBC， 122BFBC， 225 41OFOBBF， 51EFOEOF， 251251ADACDEEF ADDE的最小值为512 故选：D 二、填空题（共 4 小题） 115 12a（b+3） （b3） 137 1430 122 提示： （1）先证明ACQBAQCBQ，从而得到QABQBCQCAQACQBAQCB，进
12、而即可求解.（2）QAB+QAC45，QABQCA，QAC+QCA45，AQC135， 同理可得BQA135，QACQBA，BQC90， 22AQCQACBQAQAB，1:2QACQBASS， 设AQm，则2BQm，22CQm. 在RtQCB中，222BQCQBC，即222222mmBC，102BCm， 21212222QCBSmmm，222110132224QACQBAABCQCBSSSSmmm， 22131344QACSmm，22231342QBASmm，222111:42:2 221:QACQBAQCBSSSmmm . 三、解答题 15.原式33 352 3142 952 3 1 2 3
13、 3 16.解：设甲带了 x 两银子，乙带了 y 两银子， 根据题意得：10101010510 xyxyy， 解方程组得3818xy， 答：甲带了 38 两银子，乙带了 18 两银子 17.（1）如图，A1B1C 为所作，点 B1的坐标为（0，0） ； （2）如图，A2B2C2为所作 18.解： （1）第 6 个等式：112112866； （2）猜想的第n个等式：2121122nnnn 证明：左边21221122nnnnnnn右边， 等式成立 19.解：过点 A 作 AECD 于点 E，则AECAED90 在 RtAED 中，ADC37， cos370.85DEDEAD， 4DE ， sin3
14、70.65AEAEAD， AE3， 在 RtAEC 中， CAE90ACE906030， 333CEAE， 22 3ACCE， 2 3343 349.2ABACCEED（米） 答：这棵大树 AB 原来的高度约是 9.2 米 答：这棵大树 AB 原来的高度约是 9.2 米 20.（1）证明：延长 DE 交O 于点 G，如图所示： AB 为O 的直径，DEAB， DEGE，BDBG， D 是BC的中点， CDBDBG， BCDG， BCDG2DE； （2）解：连接 BD、OD，如图所示： CDBG， DBCBDF， DFBF， AB 为O 的直径，AB10， ACB90，OBOD5， 222210
15、68BCABAC， 由（1）得：142DEBC， DEAB， 2222543OEODDE， BEOBOE2， 设 DFBFa，则 EF4a， 在 RtBEF 中，由勾股定理得：22+（4a）2a2， 解得：52a ， 52DF 21.解： （1）调查的总人数为 816%50（人） ， 喜欢乒乓球的人数为 508206214（人） ， 所以喜欢乒乓球的学生所占的百分比14100%28%50， 故答案为：50，28%； （2）补全条形统计图如下： 50016%80， 答：全校 500 名学生中最喜欢“足球”项目的约有 80 人； （3）画树状图为： 共有 12 种等可能的结果数，其中抽取的两人恰好
16、是甲和乙的结果数为 2， 所以抽取的两人恰好是甲和乙的概率为16 22.解： （1）yx22bx4（xb）2b24， 点 A 坐标为（b，b24） ， 由 ykx 的对称性可得点 B 坐标为（b，b2+4） ， 把 xb 代入 ykx 得 ykb， kbb2+4， 联立方程 x22bx4kx 化简得 x2（2b+k）x40， xA+xB2b+k0， k2b， 把 k2b 代入kbb2+4 得 2b2b2+4， 解得 b2 或 b2（舍） k4，b2 （2）由（1）得 yx2+4x4，y4x， 设点 P 横坐标为 m，则点 P 坐标为（m，4m） ，点 C 坐标（m，0） ，点 D 坐标（m，m
17、2+4m4） ， 222117444424PDOCmmmmmmm ， PD+OC 的最大值为174 23.解： （1）CD2+BD2AD2， 理由：ABC 和ADE 是等边三角形， ABAC，ADAEDE，BACDAE60 ， BADCAE， 在ABD 和ACE 中， ABACBADCAEADAE ， ABDACE（SAS） ， BDCE， 在 RtDCE 中， CD2+CE2DE2， CD2+BD2AD2， （2）CD2+14BD2AD2， 理由：BABC2AC，DADE2AE， BABCACDADEAE， ABCADE， BACDAE， BADCAE， 12ABADACAE， BADCAE， BABDACCE2， BD2CE， 在 RtDCE 中，CD2+CE2DE2， CD2+14BD2AD2， （3） （mCD）2+（pBD）2（nAD）2， 理由：AB：BC：ACAD：DE：AEm：n：p， DEnmAD，ABCADE， BACDAE，BADCAE ABADACAE， ABDACE， BDABmCEACp， CEpmBD， 在 RtDCE 中，CD2+CE2DE2， CD2+22pmBD222nmAD2， （mCD）2+（pBD）2（nAD）2
