1、2022年温州市初中数学学业水平考试适应性卷（二）一、选择题（本题有10小题，每小题4分，共40分，每小题只有一个选项是正确的，不选、多选、错选，均不给分）1. 已知2x3y（y0），则下面结论成立的是（ ）A. B. C. D. 2. 如图，由几个小正方体组成的立体图形的俯视图是（）A. B. C. D. 3. 太阳与地球的平均距离大约是150000000 km，其中数150000000用科学记数法表示为（ ）A. 1.5108B. 15107C. 1.5107D. 0.151094. 某校950名七年级学生参加跳绳测试，随机抽取部分学生成绩并绘制频数直方图（每一组含前一个边界值，不含后一个
2、边界值）如图所示，若校方规定次数达到130次（包括130次）的成绩为“优良”，则该校成绩“优良”的学生人数约为（ ）A. 35B. 65C. 350D. 6505. 若扇形的圆心角为60，半径为4，则该扇形的面积为（ ）A B. C. D. 6. 某口罩厂平均每天可生产20万只口罩，厂家引进新技术，经过连续两次增速后，平均每天可生产30万只若两次的增长率都为x，则可得方程（ ）A. B. C. D. 7. 把直尺、三角尺和圆形螺母按如图所示的方式放置于桌面上，AB与螺母相切，D为螺母与桌面的切点，CAB=60若量出AD=6cm，则圆形螺母的外直径是（ ） A. cmB. 12cmC. cmD.
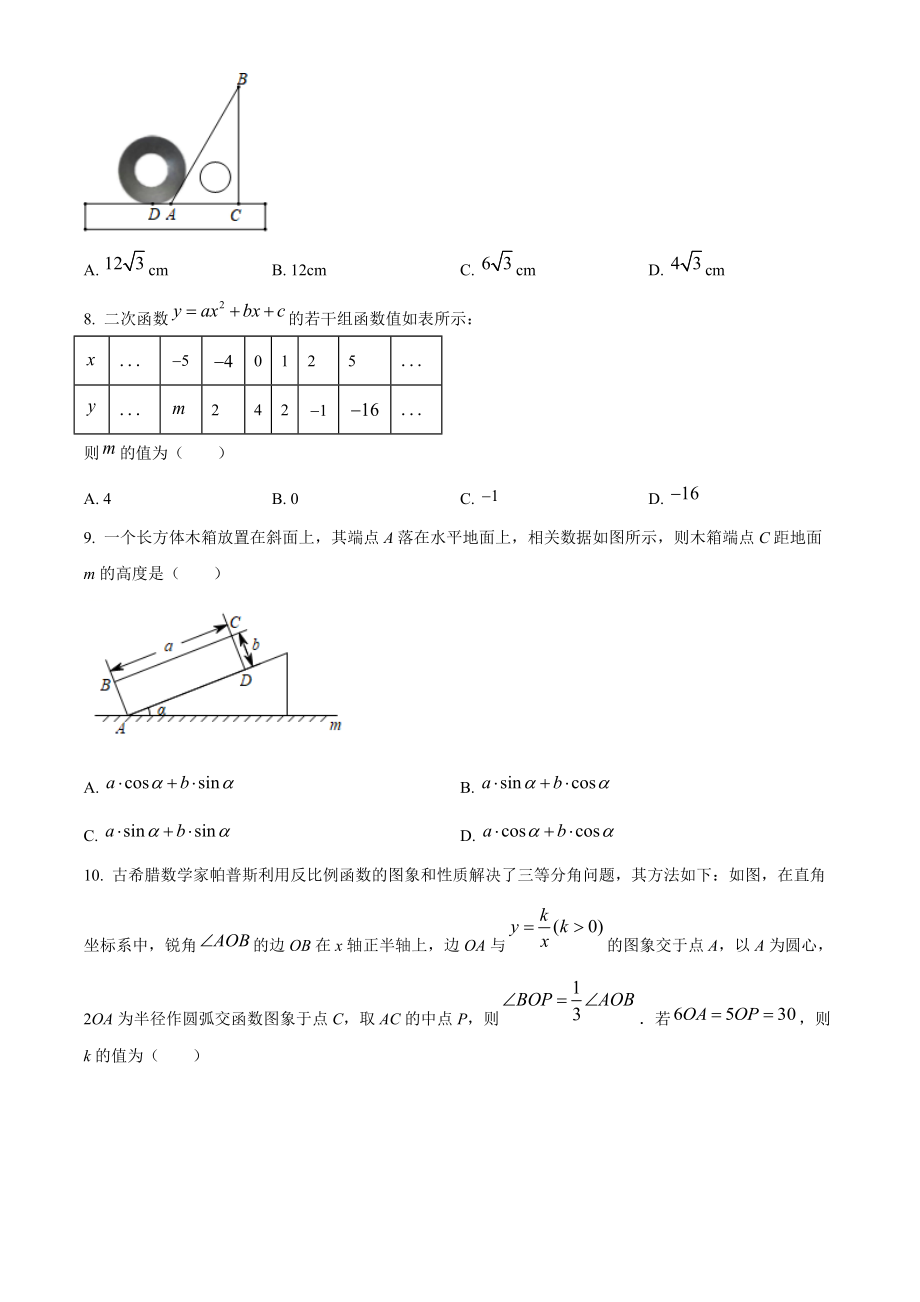
3、 cm8. 二次函数的若干组函数值如表所示：0125242则的值为（ ）A. 4B. 0C. D. 9. 一个长方体木箱放置在斜面上，其端点A落在水平地面上，相关数据如图所示，则木箱端点C距地面m的高度是（ ）A. B. C. D. 10. 古希腊数学家帕普斯利用反比例函数的图象和性质解决了三等分角问题，其方法如下：如图，在直角坐标系中，锐角的边OB在x轴正半轴上，边OA与的图象交于点A，以A为圆心，2OA为半径作圆弧交函数图象于点C，取AC的中点P，则若，则k的值为（ ）A. B. C. D. 卷二、填空题（本题有6小题，每小题5分，共30分）11. 分解因式：_12. 某商场举办有奖销售活
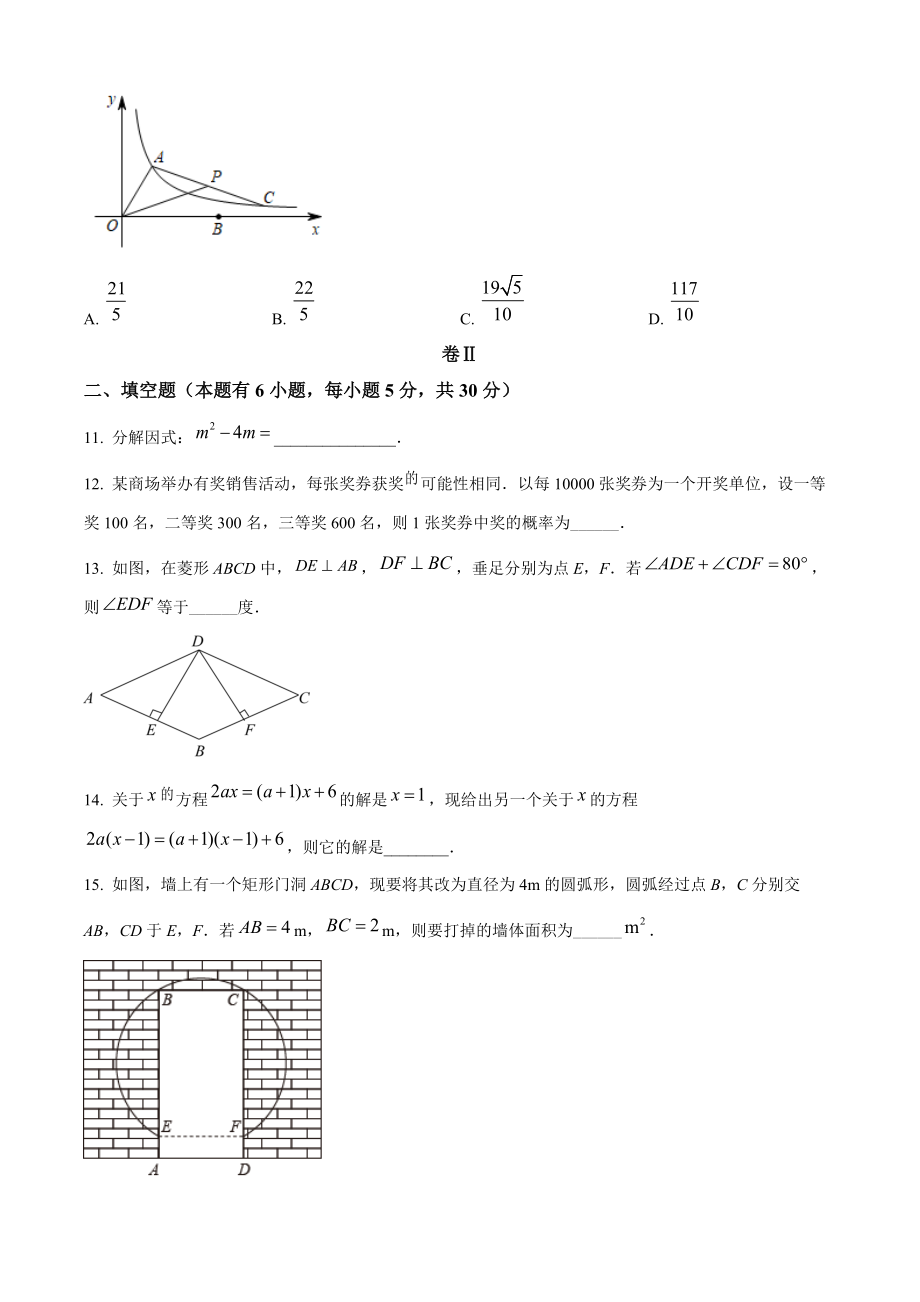
4、动，每张奖券获奖可能性相同以每10000张奖券为一个开奖单位，设一等奖100名，二等奖300名，三等奖600名，则1张奖券中奖的概率为_13. 如图，在菱形ABCD中，垂足分别为点E，F若，则等于_度14. 关于方程的解是，现给出另一个关于的方程，则它的解是_15. 如图，墙上有一个矩形门洞ABCD，现要将其改为直径为4m的圆弧形，圆弧经过点B，C分别交AB，CD于E，F若m，m，则要打掉的墙体面积为_16. 我们知道，勾股定理反映了直角三角形三条边的关系：，而，又可以看成是以a，b，c为边长的正方形的面积如图，在中，O为AB的中点,分别以AC，BC为边向外作正方形ACFG，BCED，连接OF
5、，EF，OE，则的面积为_（用含a，b的代数式表示），若，则的面积为_三、解答题（本题有8小题，共80分，解答需写出必要的文字说明、演算步骤或证明过程）17. （1）计算：（2）化简：18. 如图，四边形中，E为的中点，连结并延长交的延长线于点F（1）求证：；（2）连结，当时，求的长19. 某校策划了一次有关党的知识竞赛，每班参加比赛的人数相同，成绩分为A，B，C，D四个等级，其中相应等级的得分依次记为100分，90分，80分，70分，学校将九年级一班和二班的成绩进行整理并绘制成如下统计图请你根据以上提供的信息解答下列问题：（1）此次竞赛中，一班成绩在C级以上（包括C级）的人数为_人（2）请你
6、根据平均数、众数、中位数等统计知识，综合阐述哪个班整体水平较高，可以评为一等奖？20. 如图，是的方格纸，线段AB的两个端点分别落在格点上，请按照要求画图：（1）在图1中画一个格点四边形APBQ，且AB与PQ互相平分（2）在图2中画一个以AB为中位线的格点21. 已知抛物线经过点，（1）求，的值（2）已知为正数，当时，的最大值和最小值分别为，且，求的值22. 如图，在菱形ABCD中，点E，F分别在AD，CD边上，且，连接EF并延长EF交BC的延长线于点G（1）求证：（2）连接BE，BF，当，时，求的值23. 某中学为筹备校庆，准备印制一批纪念册该纪念册每册需要10张纸，其中4张彩色页，6张黑白
7、页印刷该纪念册的总费用由制版费和印刷费两部分组成，制版费与印数无关，价格为2200元，印刷费与印数的关系见表印数a（千册）彩色（元/张）212黑白（元/张）0.80.5（1）若印制2千册，则共需多少元？（2）该校先印制了x千册纪念册，后发现统计失误，补印了y（）千册纪念册，且补印时无需再次缴纳制版费，学校发现补印的单册造价便宜了，但两次缴纳费用恰好相同用含x的代数式表示y若该校没有统计错误，一次性打印全部纪念册，最少需要多少钱？24. 如图，已知AB是O的直径，P是半径OB上一点，作弦交O于点C，D，其中，E是上一点，延长AE交CD的延长线于点F，延长BD交EF于点G，连结DE（1）求证：（2
8、）连结BC，当四边形BCEG中有一组对边平行时，求DE的长（3）当时，求的值2022年温州市初中数学学业水平考试适应性卷（二）一、选择题（本题有10小题，每小题4分，共40分，每小题只有一个选项是正确的，不选、多选、错选，均不给分）1. 已知2x3y（y0），则下面结论成立的是（ ）A. B. C. D. 【1题答案】【答案】A【解析】【分析】根据比例的性质，把比例式写成乘积式判断即可【详解】A： 可以推出：2x3y，本选项正确； B ：可以推出：xy6；本选项错误；C： 可以推出：3x2y；本选项错误； D： 可以推出：3x2y；本选项错误；故答案选：A【点睛】本题考查比例的性质，熟练掌握基
9、本知识是解题的关键2. 如图，由几个小正方体组成的立体图形的俯视图是（）A. B. C. D. 【2题答案】【答案】D【解析】【分析】看几个小正方体组成的立体图形的俯视图，俯视图是要求从上面向下看得到的图形是俯视图，从上面看到两行小正方形，第一行一个，排在最右边，第二行看到三个小正方形最右边小正方形与前行对齐即可【详解】解：从上面看易得：有两行小正方形，第二行边有3个正方形第一行有1个正方形排在第二行前边，而且与最右侧的小正方形对齐故选择：D【点睛】本题考查组合立体图形的三视图问题，掌握主视图，左视图，即俯视图的区别与联系，它们要长对正，高平齐，宽相等，注意三视图的位置3. 太阳与地球的平均距
10、离大约是150000000 km，其中数150000000用科学记数法表示为（ ）A. 1.5108B. 15107C. 1.5107D. 0.15109【3题答案】【答案】A【解析】【分析】科学记数法的表示形式为a10n的形式，其中1|a|10，n为整数确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同【详解】解：150000000=1.5108，故选：A【点睛】本题考查了科学记数法的表示方法科学记数法的表示形式为a10n的形式，其中1|a|10，n为整数，表示时关键要正确确定a的值以及n的值4. 某校950名七年级学生参加跳绳测试，随机抽取部分学生成绩并
11、绘制频数直方图（每一组含前一个边界值，不含后一个边界值）如图所示，若校方规定次数达到130次（包括130次）的成绩为“优良”，则该校成绩“优良”的学生人数约为（ ）A. 35B. 65C. 350D. 650【4题答案】【答案】C【解析】【分析】先求出样本中“优良”成绩的人数所占的比例，再用总人数950乘以这个比例即可求解【详解】解：样本中“优良”成绩的人数所占的比例为：，该校成绩“优良”的学生人数约为950350故选：C【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题也考查了用样本估计总体5.
12、 若扇形的圆心角为60，半径为4，则该扇形的面积为（ ）A. B. C. D. 【5题答案】【答案】C【解析】【分析】直接根据扇形的面积公式即可得出结论【详解】解：扇形的圆心角为60，半径r=4，这个扇形的面积，故选：C【点睛】本题考查的是扇形面积的计算，熟记扇形的面积公式是解答此题的关键6. 某口罩厂平均每天可生产20万只口罩，厂家引进新技术，经过连续两次增速后，平均每天可生产30万只若两次的增长率都为x，则可得方程（ ）A. B. C. D. 【6题答案】【答案】B【解析】【分析】利用经过连续两次增速后的生产量=原生产量（1+平均每次增长的百分率）2，即可得出关于x的一元二次方程，此题得解
13、【详解】解：设两次的增长率都为x，依题意得：20（1+x）2=30故选：B【点睛】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键7. 把直尺、三角尺和圆形螺母按如图所示的方式放置于桌面上，AB与螺母相切，D为螺母与桌面的切点，CAB=60若量出AD=6cm，则圆形螺母的外直径是（ ） A. cmB. 12cmC. cmD. cm【7题答案】【答案】A【解析】【分析】设圆形螺母的圆心为O，连接OD，OE，OA，如图所示：根据切线的性质得到AO为DAB的平分线，ODAC，又CAB=60，得到OAE=OAD=DAB=60，根据三角函数的定义求出OD的长，即为圆
14、的半径，进而确定出圆的直径【详解】解：设圆形螺母的圆心为O，与AB切于E，连接OD，OE，OA，如图所示：AD，AB分别为圆O的切线，AO为DAB的平分线，ODAC，ODAC，又CAB=60，OAE=OAD=DAB=60，在RtAOD中，OAD=60，AD=6cm，tanOAD=tan60=，即，OD=6cm，则圆形螺母的直径为12cm故选：A【点睛】本题考查了切线的性质，切线长定理，锐角三角函数定义，以及特殊角的三角函数值，熟练掌握性质及定理是解本题的关键8. 二次函数的若干组函数值如表所示：0125242则的值为（ ）A. 4B. 0C. D. 【8题答案】【答案】C【解析】【分析】根据表
15、格可求出该二次函数的对称轴，即可证明当时和时，y的值相等，即可求出m的值【详解】当时，；当时，该二次函数的对称轴为，对于横坐标-5和2关于此对称轴对称，当时和时，y的值相等m=-1故选C【点睛】本题考查二次函数的性质根据表格求出该二次函数的对称轴是解答本题的关键9. 一个长方体木箱放置在斜面上，其端点A落在水平地面上，相关数据如图所示，则木箱端点C距地面m的高度是（ ）A. B. C. D. 【9题答案】【答案】B【解析】【分析】过点C作地面于，交AD于，过点作于，地面于，由此得到四边形DEFG是矩形，在中，解得，在中，解得，最后根据解题即可【详解】解：如图，过点C作地面于，交AD于，过点作于
16、，地面于，则四边形DEFG是矩形，在中，在中，故选：B【点睛】本题考查解直角三角形的应用，正确添加辅助线是解题关键10. 古希腊数学家帕普斯利用反比例函数的图象和性质解决了三等分角问题，其方法如下：如图，在直角坐标系中，锐角的边OB在x轴正半轴上，边OA与的图象交于点A，以A为圆心，2OA为半径作圆弧交函数图象于点C，取AC的中点P，则若，则k的值为（ ）A. B. C. D. 【10题答案】【答案】B【解析】【分析】作AEOB于E，ADOB，CDAE，交直线OB于Q，两平行线交于点D，作CFAD，交AE于F，设点A、点C坐标，求出OP解析式，证四边形AFCD是矩形，再根据已知得出OA=5，O
17、F=1，利用坐标列出方程求解即可【详解】解：作AEOB于E，ADOB，CDAE，交直线OB于Q，两平行线交于点D，作CFAD，交AE于F，则四边形AFCD是矩形；FD经过点P，设点A、点C坐标分别为，则D点坐标为，F点坐标为，设OD解析式为，把代入得，解得，OD解析式为，把代入得，则点F在直线OD上，四边形AFCD是矩形，AC的中点为P，EFDQ，OEFOQD，即，F点坐标为，点A坐标分别，把代入得，解得：（负值舍去），故选：B【点睛】本题考查了反比例函数求解析式、相似三角形点判定与性质，矩形的性质与判定，解题关键是熟练构建矩形和相似三角形，设点的坐标，利用勾股定理建立方程求解卷二、填空题（本
18、题有6小题，每小题5分，共30分）11. 分解因式：_【11题答案】【答案】【解析】【分析】根据提取公因式法即可因式分解【详解】故答案为：【点睛】此题主要考查因式分解，解题的关键是熟知提取公因式法的运用12. 某商场举办有奖销售活动，每张奖券获奖的可能性相同以每10000张奖券为一个开奖单位，设一等奖100名，二等奖300名，三等奖600名，则1张奖券中奖的概率为_【12题答案】【答案】【解析】【分析】用一等奖、二等奖、三等奖的数量除以奖券的总张数即可【详解】解：以每10000张奖券为一个开奖单位，设一等奖100名，二等奖300名，三等奖600名，一张奖券中奖概率为，故答案为：【点睛】本题考查
19、了概率公式：随机事件A的概率P（A）=事件A可能出现的结果数除以所有可能出现的结果数13. 如图，在菱形ABCD中，垂足分别为点E，F若，则等于_度【13题答案】【答案】50【解析】【分析】首先根据菱形的性质得出AC，ADCD，结合垂直的性质进而利用全等三角形的判定证明ADECDF，证明，根据直角三角形两锐角互余得，根据菱形的性质得，从而可求出【详解】解：DEAB，DFBCAEDCFD90，四边形ABCD是菱形，AC，ADCD，在AED和CFD中，AEDCFD（AAS）AEDCFD90 四边形ABCD是菱形，AD/BC 故答案为：50【点睛】此题主要考查了菱形的性质和全等三角形的判定等知识，根
20、据已知得出AC是解题关键14. 关于的方程的解是，现给出另一个关于的方程，则它的解是_【14题答案】【答案】2【解析】【分析】根据方程的解是，求得a，把a的值代入，转化为新的一元一次方程，求解即可【详解】方程的解是，2a=a+1+6，解得a=7，方程变形为：14（x-1）=8（x-1）+6，6（x-1）=6，x-1=1，x=2，故答案为：2【点睛】本题考查了一元一次方程的解及其解法，灵活运用方程的解代入求值，转化为新方程求解是解题的关键15. 如图，墙上有一个矩形门洞ABCD，现要将其改为直径为4m的圆弧形，圆弧经过点B，C分别交AB，CD于E，F若m，m，则要打掉的墙体面积为_【15题答案】
21、【答案】【解析】【分析】连结BF，AD，交于O，根据四边形ABCD为矩形，可得BCD=ABC=90，得出BF为直径，EC为直径，点O为圆心，根据勾股定理，利用三角函数sinBFC=，可求BFC=30，可证BOC为等边三角形，要打掉的墙体面积为S弓形BC+2S弓形CF，利用扇形面积公式及三角形面积公式即可得答案【详解】解：连结BF，AD，交于O，四边形ABCD为矩形，BCD=ABC=90，BF为直径，EC为直径，点O为圆心，OB=OC=OF，在RtBCF中，BC=2m，BF=4m，根据勾股定理，sinBFC=，BFC=30，OCF=BFC=30，BOC=2BFC=60，BOC为等边三角形，要打掉
22、的墙体面积为S弓形BC+2S弓形CF，=，=，=，=故答案为：【点睛】本题考查矩形性质，直角所对弦为直径，勾股定理，等边三角形判定与性质，锐角三角函数值求角，弓形面积，掌握矩形性质，直角所对弦为直径，勾股定理，等边三角形判定与性质，锐角三角函数值求角，弓形面积，熟记扇形面积公式，三角形面积公式是解题关键16. 我们知道，勾股定理反映了直角三角形三条边的关系：，而，又可以看成是以a，b，c为边长的正方形的面积如图，在中，O为AB的中点,分别以AC，BC为边向外作正方形ACFG，BCED，连接OF，EF，OE，则的面积为_（用含a，b的代数式表示），若，则的面积为_【16题答案】【答案】 . .
23、16【解析】【分析】连接AF、BE，即可根据对角线互相垂直求出四边形AFEB的面积，再根据O是AB的中点倍长中线，证明的面积为四边形AFEB的面积的一半即可【详解】如图，连接AF、BE，延长EO、FA交于点M正方形ACFG，BCED， ，AFBEAEBFO为AB中点，AFBE当时故答案为：、【点睛】本题考查正方形的性质、勾股定理得应用，解题的关键是根据倍长中线证明的面积为四边形AFEB的面积的一半三、解答题（本题有8小题，共80分，解答需写出必要的文字说明、演算步骤或证明过程）17. （1）计算：（2）化简：【17题答案】【答案】（1） ；（2） 【解析】分析】（1）原式先化简绝对值和计算零指
24、数幂，然后再计算加减法即可得到答案；（2）原式先去括号，然后再合并同类项即可【详解】解：（1）=（2）=【点睛】本题主要考查了绝对值，零指数幂，完全平方公式以及单项式乘以多项式等知识，熟练相关运算法则是解答本题的关键18. 如图，四边形中，E为的中点，连结并延长交的延长线于点F（1）求证：；（2）连结，当时，求的长【18题答案】【答案】（1）见解析；（2）3【解析】【分析】（1）利用AAS即可证明；（2）由可得，从而证明，得到，可得AB【详解】解：（1），为CD中点，在和中，（AAS）（2）由（1）中，在和中，（SAS），而，【点睛】本题考查了全等三角形的判定和性质，关键是根据AAS和SAS证
25、明三角形全等19. 某校策划了一次有关党的知识竞赛，每班参加比赛的人数相同，成绩分为A，B，C，D四个等级，其中相应等级的得分依次记为100分，90分，80分，70分，学校将九年级一班和二班的成绩进行整理并绘制成如下统计图请你根据以上提供的信息解答下列问题：（1）此次竞赛中，一班成绩在C级以上（包括C级）的人数为_人（2）请你根据平均数、众数、中位数等统计知识，综合阐述哪个班整体水平较高，可以评为一等奖？【1920题答案】【答案】（1）20； （2）一班可以评为一等奖【解析】【分析】（1）由条形图获取信息即可得出答案；（2）分别求出一班二班的众数，中位数，平均数，利用整体角度看中位数和90分以
26、上的百分率可得出结论【小问1详解】解：由条形统计图可知C级以上人数为6+12+2=20人，故答案为20；【小问2详解】从众数上看：一班众数为90分，二班众数为100分，二班好于一班，从中位数上看：一班中位数为90分，二班中位数为80分（因为44%+4%50%，而C级占16%），一班好于二班；从平均数上看，一班平均数为,二班平均数为，两班一样，从整体水平看，因为一班90分以上的占1825=72%，二班90分以上占44%+4%=48%，一班好于二班，一班可以评为一等奖【点睛】本题考查从条形图和扇形统计图获取信息和处理信息，从条形图求频数，中位数，众数，平均数，利用集中趋势的量进行决策20. 如图，
27、是的方格纸，线段AB的两个端点分别落在格点上，请按照要求画图：（1）在图1中画一个格点四边形APBQ，且AB与PQ互相平分（2）在图2中画一个以AB为中位线的格点【2021题答案】【答案】（1）作图见解析 （2）作图见解析【解析】【分析】（1）根据菱形的对角线互相平分的性质作图；（2）由中位线的性质作图【小问1详解】解：如下图，答案不唯一【小问2详解】如下图，答案不唯一【点睛】本题考查网格作图，涉及菱形的性质、中位线的性质等知识，是重要考点，掌握相关知识是解题关键21. 已知抛物线经过点，（1）求，的值（2）已知为正数，当时，的最大值和最小值分别为，且，求的值【21题答案】【答案】（1）b=4
28、,c=6；(2) k=1【解析】【分析】（1）将两点代入解析式即可（2）先求出抛物线的顶点坐标，再求出m，n的值，利用抛物线的增减性和，得出k的值【详解】解：（1）抛物线经过点， 解得 （2）由（1）可知抛物线的解析式为： =抛物线的顶点坐标为：（1,8）a1时，y随x的增大而减小，又当时，有最小值1+k=2k=1【点睛】本题考查抛物线的解析式、抛物线图像性质、在自变量范围内取最值的知识弄清抛物线的最值的取得与自变量的取值范围有紧密的联系是关键22. 如图，在菱形ABCD中，点E，F分别在AD，CD边上，且，连接EF并延长EF交BC的延长线于点G（1）求证：（2）连接BE，BF，当，时，求的值
29、【2223题答案】【答案】（1）证明见解析 （2）【解析】【分析】（1）连接AC，在菱形ABCD中，四条边都相等，再一对角相等两组边等比例的两个三角形相似，得出，再根据两组边分别平行的四边形是平行四边形，而平行四边形对角相等，根据已知条件即可得出所证；（2）连接BD交EF于点I，交AC于点H，进而得出，设，可求出，最后求出的值【小问1详解】解：连接AC，在菱形ABCD中，四边形AEGC为平行四边形，【小问2详解】解：连接BD交EF于点I，交AC于点H如图在菱形ABCD中， ，设，则，【点睛】本题主要考查了菱形的性质、相似三角形的判定与性质以及全等三角形的性质和判定，能准确分析图形中线段与角的关
30、系和牢固掌握菱形的性质、相似三角形、全等三角形的基本知识是做出本题的关键23. 某中学为筹备校庆，准备印制一批纪念册该纪念册每册需要10张纸，其中4张彩色页，6张黑白页印刷该纪念册的总费用由制版费和印刷费两部分组成，制版费与印数无关，价格为2200元，印刷费与印数的关系见表印数a（千册）彩色（元/张）212黑白（元/张）0.80.5（1）若印制2千册，则共需多少元？（2）该校先印制了x千册纪念册，后发现统计失误，补印了y（）千册纪念册，且补印时无需再次缴纳制版费，学校发现补印的单册造价便宜了，但两次缴纳费用恰好相同用含x的代数式表示y若该校没有统计错误，一次性打印全部纪念册，最少需要多少钱？【
31、23题答案】【答案】（1）28600元；（2）；101200元【解析】【分析】（1）先根据印制的册数确定彩色页和黑白页的单价，然后计算出彩色页和黑白页的总页数，最后计算需要的钱数即可得到答案（2）分和两种情况进行讨论，根据两次缴纳的费用相同列等量关系即可得到答案；先算出总册数，然后算出相应的彩色页和黑白页的单价和页数，最后进行计算即可【详解】解：（1）印制的册数为2千册，彩色页的单价为2.1元每张，彩色页的页数=20004=8000页，黑白页的单价为0.8元每张，黑白页的页数=20006=12000页，需要费用=2200+2.18000+0.812000=28600（元），故一共需要28600
32、元；（2）第一种情况当时，即，即；第二种情况当时，即，设两次一共需要印刷的册数为m，需要的钱数为W，则，故，故当，时所需要的的钱数最少为101200元【点睛】本题主要考查了一次函数与实际问题的应用，解题的关键在于分类讨论各种情况进行分析求解24. 如图，已知AB是O的直径，P是半径OB上一点，作弦交O于点C，D，其中，E是上一点，延长AE交CD的延长线于点F，延长BD交EF于点G，连结DE（1）求证：（2）连结BC，当四边形BCEG中有一组对边平行时，求DE的长（3）当时，求的值【2426题答案】【答案】（1）证明见解析 （2）6 （3）【解析】【分析】（1）由平角的定义及圆内接四边形的内对角
33、互补解得，再由同弧所对的圆周角相等得到，据此解答即可得结论；（2）根据两直线平行，同位角相等解得，同圆内，由弧相等弦相等得到，再由垂径定理解得，OC=5，由勾股定理解出OP，BC的长，由两直线平行，内错角相等得到，最后由同位角相等，证得，即可解得CE为的直径，据此解答即可答案；（3）在中，由正切定义解得，由圆周角定理证得，继而证明，最后由相似三角形对应边成比例解答即可得答案【小问1详解】解：（1），直径，小问2详解】当时，则，直径，当时，则，CE为的直径，【小问3详解】在中，【点睛】本题考查圆的综合题，涉及圆周角定理、直径所对的圆周角为90、垂径定理、正切、平行线的判定与性质、相似三角形的判定与性质等知识，是重要考点，难度一般，掌握相关知识是解题关键
