1、 2021 年浙江省宁波市宁海县年浙江省宁波市宁海县二校联考二校联考中考数学三模试卷中考数学三模试卷 一、选择题（本大题共一、选择题（本大题共 10 题，共题，共 40 分，每题分，每题 4 分）分） 1 （4 分）计算：3+1 的结果为（ ） A4 B2 C4 D2 2 （4 分）教育部预测，2021 年高校毕业生将首次突破 900 万人达到 9090000 人，9090000 用科学记数法表示为（ ） A0.909107 B9.09106 C90.9105 D909104 3 （4 分）如图所示的立体图形的主视图是（ ） A B C D 4 （4 分）下列运算结果正确的是（ ） A （a2
2、）3a5 B （ab）2a2b2 Ca3+a3a6 Da3a2a 5 （4 分）如图，在ABC 中，BAC32，将ABC 绕点 A 逆时针旋转 60得到ABC，则BAC 的度数为（ ） A28 B30 C32 D38 6（4 分） 如图是小宁连续两周居家记录的体温情况折线统计图， 下列从图中获得的信息不正确的是 （ ） A第一周体温的中位数为 37.1 B这两周体温的众数为 36.6 C第一周平均体温高于第二周平均体温 D第二周的体温比第一周的体温更加平稳 7 （4 分）如图ABC 是一个锐角，以点 A 为圆心，适当长度为半径画弧，交射线 BC 于点 D，E，若ABC35，BAD30，则DAE
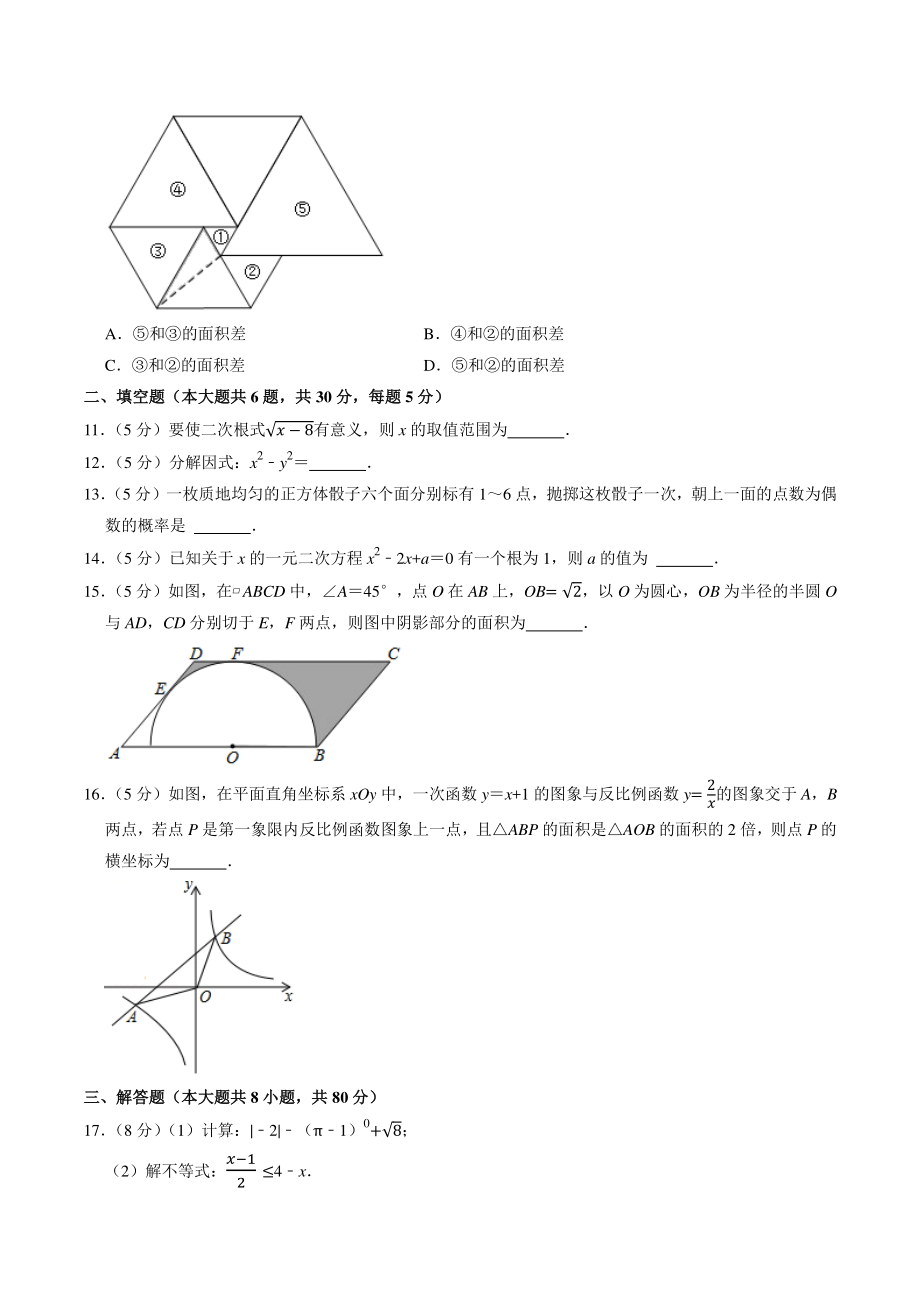
3、 的度数是（ ） A40 B50 C60 D70 8 （4 分）如图，四边形 ABCD 为平行四边形，若将ACB 沿对角线 AC 翻折得到ACE，连接 ED，则图中与CAD 度数一定相等（除CAD 外）的角的个数有（ ） A2 个 B4 个 C5 个 D7 个 9 （4 分）已知二次函数 yx22bx+6b 的顶点为（m，n） ，当 1ma 时，5n9，则 a 的取值范围为（ ） A1a3 B3a5 C3a5 D5a7 10 （4 分）如图是由 7 个等边三角形拼成的图形，若要求出阴影部分的面积，则只需要知道（ ） A和的面积差 B和的面积差 C和的面积差 D和的面积差 二、填空题（本大题共二
4、、填空题（本大题共 6 题，共题，共 30 分，每题分，每题 5 分）分） 11 （5 分）要使二次根式 8有意义，则 x 的取值范围为 12 （5 分）分解因式：x2y2 13 （5 分）一枚质地均匀的正方体骰子六个面分别标有 16 点，抛掷这枚骰子一次，朝上一面的点数为偶数的概率是 14 （5 分）已知关于 x 的一元二次方程 x22x+a0 有一个根为 1，则 a 的值为 15 （5 分）如图，在ABCD 中，A45，点 O 在 AB 上，OB= 2，以 O 为圆心，OB 为半径的半圆 O与 AD，CD 分别切于 E，F 两点，则图中阴影部分的面积为 16 （5 分）如图，在平面直角坐标
5、系 xOy 中，一次函数 yx+1 的图象与反比例函数 y=2的图象交于 A，B两点，若点 P 是第一象限内反比例函数图象上一点，且ABP 的面积是AOB 的面积的 2 倍，则点 P 的横坐标为 三、解答题（本大题共三、解答题（本大题共 8 小题，共小题，共 80 分）分） 17 （8 分） （1）计算：|2|（1）0+8； （2）解不等式：124x 18 （8 分）在正方形网格中，仅用无刻度直尺按下列要求作图 （1）如图中，在 AB 上找点 C，使得 AC：BC2：3； （2）在图中作DAB 使得 tanDAB=35 19 （8 分）中国“祝融号”火星车预计在 2021 年 5 月中下旬登陆
6、火星某一时间，太阳、地球、火星的相对位置如图所示：BCBA，A37，火星与太阳的距离 AC 为 2.4 亿千米求此时地球与火星的距离 BC （精确到 0.1 亿千米，参考数据：sin370.60，cos370.80，tan370.75） 20 （10 分）近年来，随着人们健康睡眠的意识不断提高，社会各界对于初中生的睡眠时间是否充足越发关注近日我市某学校从全校 1200 人中随机抽取了部分同学，调查他们平均每日睡眠时间，将得到的数据整理后绘制了如图所示的扇形统计图和频数分布直方图： （1）本次接受调查的人数为 ；图中 a ；b ；c ； （2） 某班学生小明平均每日睡眠时间为8.5小时， 请问小
7、明的睡眠时间是否达到平均水平？并说明理由 （3） 教育部 关于进一步加强中小学生睡眠管理工作的通知 文件指出， 初中生睡眠时间应达到 9 小时，试估算该校学生睡眠时间达标人数 21 （10 分）如图，抛物线 y1ax2（3a）x3a（a 为常数）与 x 轴的正半轴交于点 A，与 y 轴的负半轴交于点 B，直线 AB 的函数表达式为 y2kx3（k 为常数） （1）求 a 的值； （2）求直线 AB 的函数表达式； （3）根据图象写出当 y1y2时，x 的取值范围 22 （10 分）快车和慢车分别从 A 市和 B 市两地同时出发，匀速行驶，先相向而行，慢车到达 A 市后停止行驶， 快车到达 B
8、市后， 立即按原路原速度返回 A 市 （调头时间忽略不计） 结果与慢车同时到达 A 市 快、慢两车距 B 市的路程 y1、y2（单位：km）与出发时间 x（单位 h）之间的函数图象如图所示 （1）A 市和 B 市之间的路程是 km； （2）求 a 的值并解释图中点 M 的横坐标、纵坐标的实际意义； （3）快车与慢车迎面相遇以后，再经过多长时间两车相距 90km？ 23 （12 分） 【基础巩固】 （1）如图，ABCACDCED，求证：ABCCED 【尝试应用】 （2）如图，在菱形 ABCD 中，A60，点 E，F 分别为边 AD，AB 上两点，将菱形 ABCD 沿 EF翻折，点 A 恰好落在对
9、角线 DB 上的点 P 处，若 PD2PB，求的值 【拓展提高】 （3） 如图， 在矩形 ABCD 中， 点 P 是 AD 边上一点， 连接 PB， PC， 若 PA2， PD4， BPC120，求 AB 的长 24 （14 分）如图 1，锐角ABD（ABAD）内接于M，弦 ACBD 于点 O已知M 半径为 5，且 ACBD （1）求ADB 的度数； （2）若ABO 的面积为72，求 BD 的长； （3）如图 2，在（2）的条件下，点 E，F 分别在 OD，MD 上，连接 EF，ME，若DEFDAB，求MEF 面积的最大值 答案与解析答案与解析 一、选择题（本大题共一、选择题（本大题共 10
10、题，共题，共 40 分，每题分，每题 4 分）分） 1 （4 分）计算：3+1 的结果为（ ） A4 B2 C4 D2 【分析】根据有理数的加法法则，首先确定符号是负号，再用绝对值相减即可求得 【解答】解：3+12 故选：B 2 （4 分）教育部预测，2021 年高校毕业生将首次突破 900 万人达到 9090000 人，9090000 用科学记数法表示为（ ） A0.909107 B9.09106 C90.9105 D909104 【分析】科学记数法的表示形式为 a10n的形式，其中 1|a|10，n 为整数确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移
11、动的位数相同当原数绝对值10 时，n是正整数，当原数绝对值1 时，n 是负整数 【解答】解：90900009.09106 故选：B 3 （4 分）如图所示的立体图形的主视图是（ ） A B C D 【分析】根据从正面看得到的图形是主视图，可得答案 【解答】解：从正面看，底层是一个较大的矩形，上层中间是一个较小的矩形，且中间有一条纵向的实线 故选：A 4 （4 分）下列运算结果正确的是（ ） A （a2）3a5 B （ab）2a2b2 Ca3+a3a6 Da3a2a 【分析】各式计算得到结果，即可作出判断 【解答】解：原式a6，不符合题意； B、原式a2+b2+2ab，不符合题意； C、原式2a
12、3，不符合题意； D、原式a，符合题意 故选：D 5 （4 分）如图，在ABC 中，BAC32，将ABC 绕点 A 逆时针旋转 60得到ABC，则BAC 的度数为（ ） A28 B30 C32 D38 【分析】由旋转的性质可得BAB60，即可求解 【解答】解：将ABC 绕点 A 逆时针旋转 60得到ABC， BAB60， BACBABBAC28， 故选：A 6（4 分） 如图是小宁连续两周居家记录的体温情况折线统计图， 下列从图中获得的信息不正确的是 （ ） A第一周体温的中位数为 37.1 B这两周体温的众数为 36.6 C第一周平均体温高于第二周平均体温 D第二周的体温比第一周的体温更加平
13、稳 【分析】根据统计图和中位数、众数、平均数的定义分别进行解答，即可求出答案 【解答】解：A第一周体温的中位数为 36.9，信息不正确，故本选项符合题意； B这两周体温 36.6出现的次数最多，是 5 次，所以，众数是 36.6，信息正确，故本选项不符合题意； C第一周平均体温是17（36.7+37.1+36.6+37.1+37.1+36.6+36.9）36.9（） ，第二周平均体温17（36.7+36.6+36.7+36.8+36.6+36.6+36.8）36.7（） ，第一周平均体温高于第二周平均体温，故本选项不符合题意； D根据折线统计图可得：第二周的体温比第一周的体温更加平稳，信息正确
14、，故本选项不符合题意 故选：A 7 （4 分）如图ABC 是一个锐角，以点 A 为圆心，适当长度为半径画弧，交射线 BC 于点 D，E，若ABC35，BAD30，则DAE 的度数是（ ） A40 B50 C60 D70 【分析】 根据三角形外角的性质可得到ADE的度数， 再根据等腰三角形的性质以及三角形内角和定理，即可得到DAE 的度数 【解答】解：ABC35，BAD30， ADEABC+BAD65， 由作图可得，ADAE， AEDADE65， ADE 中，DAE180ADEAED180656550， 故选：B 8 （4 分）如图，四边形 ABCD 为平行四边形，若将ACB 沿对角线 AC 翻
15、折得到ACE，连接 ED，则图中与CAD 度数一定相等（除CAD 外）的角的个数有（ ） A2 个 B4 个 C5 个 D7 个 【分析】根据平行四边形的性质、折叠的性质以及全等三角形的性质解答即可 【解答】解：设 AD 与 CE 交点为 O 四边形 ABCD 为平行四边形， ABCD，BODC，ADBC， CADACB， 由折叠可知，AEAB，BAEO， AECD，AEOCDO， AOECOD， AOECOD（AAS） ， ODOE， OAOC， CADACO，OEDODE， AOCEOD， CADACOOEDODE， 因此CAD 度数一定相等的角有：ACO、OED、ODE、ACB，共 4
16、个角 故选：B 9 （4 分）已知二次函数 yx22bx+6b 的顶点为（m，n） ，当 1ma 时，5n9，则 a 的取值范围为（ ） A1a3 B3a5 C3a5 D5a7 【分析】先将题目中的函数解析式化为顶点式，然后即可得到 m 与 b 的关系和 n 与 b 的关系，再根据当1ma 时，5n9，即可求得 a 的取值范围 【解答】解：二次函数 yx22bx+6b（xb）2b2+6b，其顶点为（m，n） ， 该函数的顶点坐标为（b，b2+6b） ， mb，nb2+6b， 当 1ma 时，5n9， 1 5 2+ 6 9， 解得 3a5， 故选：B 10 （4 分）如图是由 7 个等边三角形拼
17、成的图形，若要求出阴影部分的面积，则只需要知道（ ） A和的面积差 B和的面积差 C和的面积差 D和的面积差 【分析】 （1）因全为等边三角形，所以面积差可算出边长的平方差 （2）若两个等边三角形有一条公共边，则两三个角形全等 （3）阴影部分面积可由的面积减去的边长乘的高得到 【解答】设每个等边三角形边长为 xn，每个三角形面积为34xn2 阴影部分面积 S=34x3（x3x2） x1x3x2，x1+x3x4， 与面积差等于34（x42x22）=34（x4+x2） （x4x2） x1x3x2，x1+x3x4， 化简得3x3（x3x2） 观察上式可得阴影面积与与面积差相差四倍，则只需知道和的面积
18、差 故选：B 二、填空题（本大题共二、填空题（本大题共 6 题，共题，共 30 分，每题分，每题 5 分）分） 11 （5 分）要使二次根式 8有意义，则 x 的取值范围为 x8 【分析】直接利用二次根式的定义得出答案 【解答】解：要使二次根式 8有意义， 则 x80， 解得：x8 故答案为：x8 12 （5 分）分解因式：x2y2 （x+y） （xy） 【分析】因为是两个数的平方差，所以利用平方差公式分解即可 【解答】解：x2y2（x+y） （xy） 故答案是： （x+y） （xy） 13 （5 分）一枚质地均匀的正方体骰子六个面分别标有 16 点，抛掷这枚骰子一次，朝上一面的点数为偶数的概
19、率是 12 【分析】抛掷这枚骰子一次共有 6 种等可能结果，朝上一面的点数为偶数的有 2、4、6 这 3 种结果，再根据概率公式求解即可 【解答】解：抛掷这枚骰子一次共有 6 种等可能结果，朝上一面的点数为偶数的有 2、4、6 这 3 种结果， 所以抛掷这枚骰子一次，朝上一面的点数为偶数的概率为36=12， 故答案为：12 14 （5 分）已知关于 x 的一元二次方程 x22x+a0 有一个根为 1，则 a 的值为 1 【分析】把 x1 代入方程 x22x+a0，列出关于 a 的新方程，通过解该方程可以求得 a 的值 【解答】解：依题意得：1221+a0， 解得 a1 故答案是：1 15 （5
20、 分）如图，在ABCD 中，A45，点 O 在 AB 上，OB= 2，以 O 为圆心，OB 为半径的半圆 O 与 AD，CD 分别切于 E，F 两点，则图中阴影部分的面积为 22 +134 【分析】 连接 OE，OF，根据切线的性质即可 OEAD，OFCD，进而可得 CDABOA+OB2+2，根据 S阴影S平行四边形ABCDS半圆（SAOES扇形EOG） ，即可求图中阴影部分的面积 【解答】解：如图，连接 OE，OF， 半圆 O 与 AD，CD 分别切于 E，F 两点， OEAD，OFCD， AEO90， A45， AOE45， OEAEOBOF= 2， OA= 2+ 2=2， CDABOA+
21、OB2+2， S阴影S平行四边形ABCDS半圆（SAOES扇形EOG） （2+2） 2 12（2）2（122 2 45(2)2360 22 +21+4 22 +134 所以图中阴影部分的面积为 22 +134 故答案为：22 +134 16 （5 分）如图，在平面直角坐标系 xOy 中，一次函数 yx+1 的图象与反比例函数 y=2的图象交于 A，B两点，若点 P 是第一象限内反比例函数图象上一点，且ABP 的面积是AOB 的面积的 2 倍，则点 P 的横坐标为 2 或3+172 【分析】分点 P 在 AB 下方、点 P 在 AB 上方两种情况，分别求解即可 【解答】解：当点 P 在 AB 下
22、方时 作 AB 的平行线 l，使点 O 到直线 AB 和到直线 l 的距离相等，则ABP 的面积是AOB 的面积的 2 倍， 直线 AB 与 x 轴交点的坐标为（1，0） ，则直线 l 与 x 轴交点的坐标 C（1，0） ， 设直线 l 的表达式为：yx+b，将点 C 的坐标代入上式并解得：b1， 故直线 l 的表达式为 yx1，而反比例函数的表达式为：y=2， 联立并解得：x2 或1（舍去） ； 当点 P 在 AB 上方时， 同理可得，直线 l 的函数表达式为：yx+3， 联立并解得：x=3172（舍去负值） ； 故答案为：2 或3+172 三、解答题（本大题共三、解答题（本大题共 8 小题
23、，共小题，共 80 分）分） 17 （8 分） （1）计算：|2|（1）0+8； （2）解不等式：124x 【分析】 （1）根据绝对值，零指数幂，算术平方根的定义进行计算即可 （2）去分母，去括号，移项，合并同类项，系数化为 1 即可得出结果 【解答】解： （1）原式= 2 1 + 22 = 1 + 22 （2）去分母得：x12（4x） ， 去括号得：x182x， 移项得：x+2x8+1， 合并同类项得：3x9， 系数化为 1 得：x3 18 （8 分）在正方形网格中，仅用无刻度直尺按下列要求作图 （1）如图中，在 AB 上找点 C，使得 AC：BC2：3； （2）在图中作DAB 使得 tan
24、DAB=35 【分析】 （1）取格点 M，N，来看 MN 交 AB 于点 C，点 C 即为所求作 （2）取格点 E，连接 BE，取格点 M,N，连接 MN 交 BE 于点 D，连接 AD,ADB 即为所求作 【解答】解： （1）如图，点 C 即为所求作 （2）如图，DAB 即为所求作 19 （8 分）中国“祝融号”火星车预计在 2021 年 5 月中下旬登陆火星某一时间，太阳、地球、火星的相对位置如图所示：BCBA，A37，火星与太阳的距离 AC 为 2.4 亿千米求此时地球与火星的距离 BC （精确到 0.1 亿千米，参考数据：sin370.60，cos370.80，tan370.75） 【
25、分析】如图，过 B 作 BDAC，垂足为 D，由 BCBA 可得 CD=12AC，CA37，在 RtCDB中，根据 BCCDcos37代入计算即可得出答案 【解答】解：如图，过 B 作 BDAC，垂足为 D， BCBA CD=12AC1.2，CA37， 在 RtCDB 中， BCCDcos37 1.20.801.5（亿千米） 答：地球与火星的距离 BC 大约为 1.5 亿千米 20 （10 分）近年来，随着人们健康睡眠的意识不断提高，社会各界对于初中生的睡眠时间是否充足越发关注近日我市某学校从全校 1200 人中随机抽取了部分同学，调查他们平均每日睡眠时间，将得到的数据整理后绘制了如图所示的扇
26、形统计图和频数分布直方图： （1）本次接受调查的人数为 50 ；图中 a 28% ；b 21 ；c 20% ； （2） 某班学生小明平均每日睡眠时间为8.5小时， 请问小明的睡眠时间是否达到平均水平？并说明理由 （3） 教育部 关于进一步加强中小学生睡眠管理工作的通知 文件指出， 初中生睡眠时间应达到 9 小时，试估算该校学生睡眠时间达标人数 【分析】（1） 根据 7t8 的人数和所占的百分比， 求出调查的总人数， 再用 8t9 的人数除以总人数，求出 a；用总人数乘以 9t10 所占的百分比，求出 b；同 10t11 的人数除以总人数，即可得出 c； （2）根据平均数的计算公式先求出小明的睡
27、眠时间，再与小明平均每日睡眠时间进行比较，即可得出答案； （3）用总人数乘以该校学生睡眠时间达标人数所占的百分比即可 【解答】解： （1）本次接受调查的人数为：510%50（人） ， a=14501000%28%； b5042%21， c=1050100%21% 故答案为：50；28%；21；20%； （2）小明未达到平均水平 理由如下： =7.55+8.514+9.521+10.51050=9.22（小时） ， 8.59.22， 小明未达到平均水平 （3）根据题意得：120021+1050=744（人） ， 答：共有 744 人睡眠时间达标 21 （10 分）如图，抛物线 y1ax2（3a）
28、x3a（a 为常数）与 x 轴的正半轴交于点 A，与 y 轴的负半轴交于点 B，直线 AB 的函数表达式为 y2kx3（k 为常数） （1）求 a 的值； （2）求直线 AB 的函数表达式； （3）根据图象写出当 y1y2时，x 的取值范围 【分析】 （1）直线 AB 的函数表达式为 y2kx3，故点 B（0，3） ，抛物线 y1ax2（3a）x3a，故点 B（0，3） ，故3a3，即可求解； （2）由抛物线的表达式求出 A（3，0） ，将点 A 的坐标代入直线 AB 的表达式，即可求解； （3）观察图象即可求解 【解答】解： （1）直线 AB 的函数表达式为 y2kx3，令 x0，则 y3，
29、故点 B（0，3） ， 抛物线 y1ax2（3a）x3a，故点 B（0，3） ， 故3a3，解得：a1； （2）a1， 故抛物线的表达式为：yx22x3，令 y0，则 x1 或 3，故点 A（3，0） ， 将点 A 的坐标代入直线 AB 的表达式并解得：k1， 故直线 AB 的表达式为：yx3； （3）从图象看，x0 或 x3 时，y1y2 22 （10 分）快车和慢车分别从 A 市和 B 市两地同时出发，匀速行驶，先相向而行，慢车到达 A 市后停止行驶， 快车到达 B 市后， 立即按原路原速度返回 A 市 （调头时间忽略不计） 结果与慢车同时到达 A 市 快、慢两车距 B 市的路程 y1、y
30、2（单位：km）与出发时间 x（单位 h）之间的函数图象如图所示 （1）A 市和 B 市之间的路程是 360 km； （2）求 a 的值并解释图中点 M 的横坐标、纵坐标的实际意义； （3）快车与慢车迎面相遇以后，再经过多长时间两车相距 90km？ 【分析】 （1）根据函数图象直接可以得到 A 市和 B 市之间的路程； （2）由题意可得，快车速度是慢车速度的 2 倍，即可得快车的速度为 120（千米/小时） ，慢车的速度为60（千米/小时） ，故 a602120，点 M 的横坐标实际意义是快车与慢车出发后经过 2 小时相遇，纵坐标的实际意义是快车与慢车相遇时距 B 地 120 千米； （3）根
31、据函数图象中的数据，可以求得 y1与 x 之间的函数关系式，再利用分类讨论的方法，可以得到快车与慢车迎面相遇以后，再经过12小时或52小时两车相距 90km 【解答】解： （1）由图象可得，A 市和 B 市之间的路程是 360km， 故答案为：360； （2）由题意可得，快车速度是慢车速度的 2 倍， 快车的速度为：360223=120（千米/小时） ，慢车的速度为 120260（千米/小时） ， a602120， 点 M 的横坐标实际意义是快车与慢车出发后经过 2 小时相遇， 纵坐标的实际意义是快车与慢车相遇时距B 地 120 千米； （3）快车从 A 市到 B 市用的时间为 3601203
32、（小时） ， 设当 0 x3 时，y1与 x 之间的函数关系式 y1kx+b， = 3602 + = 120，解得 = 120 = 360， 当 0 x3 时，y1与 x 之间的函数关系式 y1120 x+360； 在 y1120 x+360 中，令 y0 得 x3， 快车在 x3 时到达 B 市， 快车在 x6 时返回 A 市， 设当 3x6 时，y1与 x 之间的函数关系式 y1mx+n， 3 + = 06 + = 360，解得 = 120 = 360， 当 3x6 时，y1与 x 之间的函数关系式 y1120 x360； 设快车与慢车迎面相遇以后，再经过 t 小时两车相距 90km， 快
33、车到达 B 市之前，120（t+2）+60（t+2）360+90，解得 t=12， 快车从 B 市前往 A 市，60（t+2）120（t+23）90，解得 t=52， 答：快车与慢车迎面相遇以后，再经过12小时或52小时两车相距 90km 23 （12 分） 【基础巩固】 （1）如图，ABCACDCED，求证：ABCCED 【尝试应用】 （2）如图，在菱形 ABCD 中，A60，点 E，F 分别为边 AD，AB 上两点，将菱形 ABCD 沿 EF翻折，点 A 恰好落在对角线 DB 上的点 P 处，若 PD2PB，求的值 【拓展提高】 （3） 如图， 在矩形 ABCD 中， 点 P 是 AD 边
34、上一点， 连接 PB， PC， 若 PA2， PD4， BPC120，求 AB 的长 【分析】 （1）ABCACD，ACEA+ABC，则AECD，进而求解； （2） 证明ABD 为等边三角形， 由 （1） 得ABCCED， 则=， 即3=23=， 即可求解； （3）证明BEPPFC，则=，即2343=2323，即可求解 【解答】解： （1）ABCACD，ACEA+ABC， DCE+A+，即AECD， ABCCED， ABCCED； （2）四边形 ABCD 为菱形， ABAD， A60， ABD 为等边三角形， EPFAADBABD60， 由（1）得：DPEBFP， =， 设 BPa，则 DP2
35、a，AEPEx，AFPFy， 则 DE3ax，BF3ay， 3=23=， 解得：=54， 的值为54； （3）如图，在 AD 上取点 E、F，使ABEDCF30， 四边形 ABCD 为矩形， AD90， BEPBPCPFC120， EPB+FPC18012060，EPB+EBP60， FPCEBP， BEPPFC， =， 设 ABCDm， 则2343=2323， 解得：m= 11 3或3 11（舍去） ， AB= 11 3 24 （14 分）如图 1，锐角ABD（ABAD）内接于M，弦 ACBD 于点 O已知M 半径为 5，且 ACBD （1）求ADB 的度数； （2）若ABO 的面积为72，
36、求 BD 的长； （3）如图 2，在（2）的条件下，点 E，F 分别在 OD，MD 上，连接 EF，ME，若DEFDAB，求MEF 面积的最大值 【分析】 （1）ACBD，则= ，则= ，故ADBCAD=12（18090）45； （2）在等腰直角三角形 ABM 中，AB= 2AM52 = 2+ 2，而 SABO=12AOBO=72，即 AOBO7，即可求解； （3） 证明MDHEDF， 则=， 即3=4， 故设 EF3x， 则 DF4x， 则 MF54x， S=12EFMF=123x（54x） ，即可求解 【解答】解： （1）ACBD， = ， = ， ADBCAD=12（18090）45，
37、即ADB45； （2）ADB45， 连接 AM、BM，则AMB90， 在等腰直角三角形 ABM 中，AB= 2AM52 = 2+ 2， 即 AO2+BO250， SABO=12AOBO=72，即 AOBO7， 则 AO+BO= 2+ 2+ 2 =8， BDOB+ODBO+AO8； （3）过点 M 作 MHBD，延长 MH 交圆于点 N， =12，BHDH4， 根据勾股定理得，MH3， =12， HMDDABDEF， EDFMDH， MDHEDF， EFDMHD90， =，即3=4， 故设 EF3x，则 DF4x，则 MF54x， S=12EFMF=123x（54x）6（x58）2+7532， 故当 x=58时，S 的最大值为7532
