 2022年四川省攀枝花市中考模拟数学试卷(3)含答案解析
2022年四川省攀枝花市中考模拟数学试卷(3)含答案解析
《2022年四川省攀枝花市中考模拟数学试卷(3)含答案解析》由会员分享,可在线阅读,更多相关《2022年四川省攀枝花市中考模拟数学试卷(3)含答案解析(21页珍藏版)》请在七七文库上搜索。
1、 2022 年四川省攀枝花市中考数学模拟试卷(年四川省攀枝花市中考数学模拟试卷(3) 一选择题(共一选择题(共 10 小题,满分小题,满分 40 分,每小题分,每小题 4 分)分) 1 (4 分)2 与 2m 互为相反数,那么 m 等于( ) A1 B1 C D 2 (4 分)事件“|x|0(x 为任意实数) ”是( ) A随机事件 B必然事件 C确定事件 D不可能事件 3 (4 分)如图,直线 l1l2,CDAB 于点 D,144,则2 的度数为( ) A30 B44 C46 D56 4 (4 分)下列运算结果正确的是( ) A (2x3)24x6 Bx2+x3x5 C (x)1 Dx01
2、5 (4 分)关于 x 的一元二次方程 ax24x+10 有实数根,则整数 a 的最大值是( ) A1 B4 C3 D4 6 (4 分)表示( ) A3 的平方根 B3 的立方根 C3 的算术平方根 D3 的一半 7 (4 分)2020 年春季,全球发生了新型冠状病毒疫情,病毒直径约在 100300 纳米之间,我们知道,1纳米107cm,用科学记数法表示直径为 150 纳米的病毒相当于( ) A150107cm B15106cm C1.5105cm D1.5107cm 8 (4 分)实数 a、b 在数轴上对应点如图所示,则化简|a|的结果是( ) A2a B2b C2b D2a 9 (4 分)
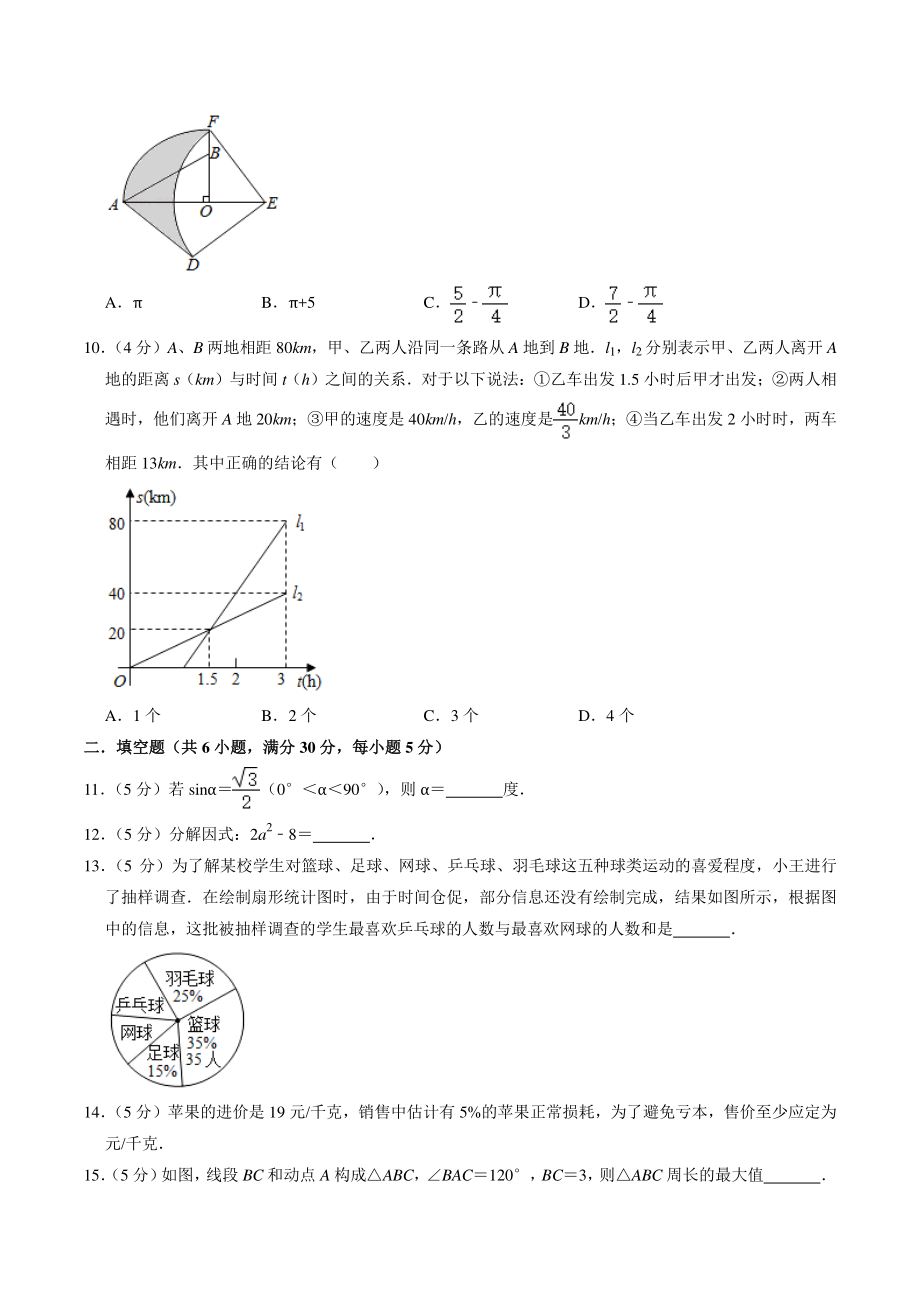
3、如图,在 RtAOB 中,AOB90,OA2,OB1,将 RtAOB 绕点 O 顺时针旋转 90后得 RtFOE,将线段 EF 绕点 E 逆时针旋转 90后得线段 ED,分别以 O,E 为圆心,OA、ED 长为半径画弧 AF 和弧 DF,连接 AD,则图中阴影部分面积是( ) A B+5 C D 10 (4 分)A、B 两地相距 80km,甲、乙两人沿同一条路从 A 地到 B 地l1,l2分别表示甲、乙两人离开 A地的距离 s(km)与时间 t(h)之间的关系对于以下说法:乙车出发 1.5 小时后甲才出发;两人相遇时,他们离开 A 地 20km;甲的速度是 40km/h,乙的速度是km/h;当
4、乙车出发 2 小时时,两车相距 13km其中正确的结论有( ) A1 个 B2 个 C3 个 D4 个 二填空题(共二填空题(共 6 小题,满分小题,满分 30 分,每小题分,每小题 5 分)分) 11 (5 分)若 sin(090) ,则 度 12 (5 分)分解因式:2a28 13 (5 分)为了解某校学生对篮球、足球、网球、乒乓球、羽毛球这五种球类运动的喜爱程度,小王进行了抽样调查在绘制扇形统计图时,由于时间仓促,部分信息还没有绘制完成,结果如图所示,根据图中的信息,这批被抽样调查的学生最喜欢乒乓球的人数与最喜欢网球的人数和是 14 (5 分)苹果的进价是 19 元/千克,销售中估计有
5、5%的苹果正常损耗,为了避免亏本,售价至少应定为 元/千克 15 (5 分) 如图, 线段 BC 和动点 A 构成ABC, BAC120, BC3, 则ABC 周长的最大值 16 (5 分)如图,正方形 ABCD 和正方形 CGFE 的顶点 C,D,E 在同一条直线上,顶点 B,C,G 在同一条直线上,O 是 EG 的中点,EGC 的平分线 GH 过点 D,交 BE 于点 H,连接 FH 交 EG 于点 M,连接OH以下四个结论:OHBE:EHMFHG:2,其中正确的结论是 三解答题(共三解答题(共 8 小题,满分小题,满分 80 分)分) 17 (6 分)求(xy1) (xy+1)(xy1)
6、2,其中 x2021,y 18 (8 分)元宵节前夕,某超市从厂家购进了甲、乙两种发光道具,甲种道具每件进价比乙种道具每件进价少 2 元若购进甲种道具 7 件,乙种道具 2 件,需要 76 元 (1)求甲、乙两种道具的每件进价分别是多少元? (2)若该超市从厂家购进了甲乙两种道具共 50 件,在销售时,甲种道具的每件售价为 10 元,乙种道具的每件售价为 15 元,要使得这 50 件道具所获利润为 160 元,应购进乙道具多少件? 19 (8 分)如图,G 是ABC 的重心,过 G 作 DEAC,分别交 AB、BC 于 D、E,再过 E 作 EFAB 交AC 于 F,求 S四边形ADEF:SA
7、BC的值 20 (10 分)如图,在平面直角坐标系中,一次函数 yx+2 的图象与 x 轴、y 轴分别交于 A、B 两点,与反比例函数 y(a0)的图象交于 P(2,m) ,Q(n,1)两点 (1)求该反比例函数的解析式; (2)求OPQ 的面积; (3)请根据图象直接写出不等式x+2的解集 21 (10 分)文具店有三种品牌的 6 个笔记本,价格是 4,5,7(单位:元)三种,从中随机拿出一个本,已知 P(一次拿到 7 元本) (1)求这 6 个笔记本价格的众数 (2)若琪琪已拿走一个 7 元笔记本,嘉嘉准备从剩余 5 个笔记本中随机拿一个本 所剩的 5 个笔记本价格的中位数与原来 6 个笔
8、记本价格的中位数是否相同?并简要说明理由; 嘉嘉先随机拿出一个笔记本后不放回,之后又随机从剩余的笔记本中拿一个本,用列表法或画树状图求嘉嘉两次都拿到 7 元本的概率 22 (12 分) 如图所示, 抛物线 yax2+bx+c 的对称轴为直线 x3, 抛物线与 x 轴交于 A (2, 0) 、 B 两点,与 y 轴交于点 C(0,4) (1)求抛物线的解析式; (2)连接 BC,在第一象限内的抛物线上,是否存在一点 P,使PBC 的面积最大?最大面积是多少? 23 (12 分)如图,信号塔 PQ 座落在坡度 i1:2 的山坡上,其正前方直立着一警示牌当太阳光线与水平线成 60角时,测得信号塔 P
9、Q 落在斜坡上的影子 QN 长为 2米,落在警示牌上的影子 MN 长为 3米,求信号塔 PQ 的高 (结果不取近似值) 24 (14 分) (1)问题发现 如图 1,在 RtABC 和 RtCDE 中,ACBDCE90,CABCDE45,点 D 是线段 AB上一动点,连接 BE 填空: 的值为 ; DBE 的度数为 (2)类比探究 如图 2,在 RtABC 和 RtCDE 中,ACBDCE90,CABCDE60,点 D 是线段 AB上一动点,连接 BE请求出的值及DBE 的度数,并说明理由; (3)拓展延伸 如图 3,在 RtABC 和 RtCDE 中,ACBDCE90,CABCDE,点 D
10、是线段 AB 上一动点,连接 BE,P 为 DE 中点若 BC4,AC3,在点 D 从 A 点运动到 B 点的过程中,请直接写出 P 点经过的路径长 2022 年四川省攀枝花市中考数学模拟试卷(年四川省攀枝花市中考数学模拟试卷(3) 参考答案与试题解析参考答案与试题解析 一选择题(共一选择题(共 10 小题,满分小题,满分 30 分,每小题分,每小题 3 分)分) 1 (4 分)2 与 2m 互为相反数,那么 m 等于( ) A1 B1 C D 【解答】解:2 与 2m 互为相反数, 2+2m0, 解得 m1, 故选:B 2 (4 分)事件“|x|0(x 为任意实数) ”是( ) A随机事件
11、B必然事件 C确定事件 D不可能事件 【解答】解:|x|0,是随机事件,只有 x0 时,是必然事件 故选:A 3 (4 分)如图,直线 l1l2,CDAB 于点 D,144,则2 的度数为( ) A30 B44 C46 D56 【解答】解:CDAB 于点 D,144, CBD46, 直线 l1l2, CBD2, 246, 故选:C 4 (4 分)下列运算结果正确的是( ) A (2x3)24x6 Bx2+x3x5 C (x)1 Dx01 【解答】解:A、 (2x3)24x6,正确; B、x2+x3,无法计算,故此选项错误; C、 (x)1,故此选项错误; D、x01(x0) ,故此选项错误;
12、故选:A 5 (4 分)关于 x 的一元二次方程 ax24x+10 有实数根,则整数 a 的最大值是( ) A1 B4 C3 D4 【解答】解:由题意可知:164a0 且 a0, a4 且 a0, 所以 a 的最大值为 4, 故选:D 6 (4 分)表示( ) A3 的平方根 B3 的立方根 C3 的算术平方根 D3 的一半 【解答】解:表示 3 的算术平方根, 故选:C 7 (4 分)2020 年春季,全球发生了新型冠状病毒疫情,病毒直径约在 100300 纳米之间,我们知道,1纳米107cm,用科学记数法表示直径为 150 纳米的病毒相当于( ) A150107cm B15106cm C1
13、.5105cm D1.5107cm 【解答】解:150 纳米150107cm1.5105cm, 故选:C 8 (4 分)实数 a、b 在数轴上对应点如图所示,则化简|a|的结果是( ) A2a B2b C2b D2a 【解答】解:如图所示:b0,ab0,a0, 则|a| b+ba(a) 2b 故选:B 9 (4 分)如图,在 RtAOB 中,AOB90,OA2,OB1,将 RtAOB 绕点 O 顺时针旋转 90后得 RtFOE,将线段 EF 绕点 E 逆时针旋转 90后得线段 ED,分别以 O,E 为圆心,OA、ED 长为半径画弧 AF 和弧 DF,连接 AD,则图中阴影部分面积是( ) A
14、B+5 C D 【解答】解:作 DHAE 于 H, AOB90,OA2,OB1, AB, 由旋转,得EOFBOA, OABEFO, FEO+EFOFEO+HED90, EFOHED, HEDOAB, DHEAOB90,DEAB, DHEBOA(AAS) , DHOB1, 阴影部分面积ADE 的面积+EOF 的面积+扇形 AOF 的面积扇形 DEF 的面积 31+12+ , 故选:C 10 (4 分)A、B 两地相距 80km,甲、乙两人沿同一条路从 A 地到 B 地l1,l2分别表示甲、乙两人离开 A地的距离 s(km)与时间 t(h)之间的关系对于以下说法:乙车出发 1.5 小时后甲才出发;
15、两人相遇时,他们离开 A 地 20km;甲的速度是 40km/h,乙的速度是km/h;当乙车出发 2 小时时,两车相距 13km其中正确的结论有( ) A1 个 B2 个 C3 个 D4 个 【解答】解:由图象可得, 乙车出发 1.5 小时后甲乙相遇,故错误; 两人相遇时,他们离开 A 地 20km,故正确; 甲的速度是(8020)(31.5)40(km/h) ,乙的速度是km/h,故正确; 当乙车出发 2 小时时,两车相距:20+(21.5)402km,故错误; 故选:B 二填空题(共二填空题(共 6 小题,满分小题,满分 30 分,每小题分,每小题 5 分)分) 11 (5 分)若 sin


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2022 四川省 攀枝花市 中考 模拟 数学试卷 答案 解析
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-209549.html