 2022年北京市中考模拟数学试卷(3)含答案解析
2022年北京市中考模拟数学试卷(3)含答案解析
《2022年北京市中考模拟数学试卷(3)含答案解析》由会员分享,可在线阅读,更多相关《2022年北京市中考模拟数学试卷(3)含答案解析(28页珍藏版)》请在七七文库上搜索。
1、2022 年年北京市北京市中考中考模拟模拟数学数学试题(试题(3) 一、选择题一、选择题(共共 16 分,每题分,每题 2 分分)第第 1-8 题均有四个选项,符合题意的选项只有一个。题均有四个选项,符合题意的选项只有一个。 1(2 分)下列几何体中,其面既有平面又有曲面的有( ) A1 个 B2 个 C3 个 D4 个 2(2 分)实数 a、b 在数轴上的位置如图,则化简|a|+|b|的结果为( ) Aab Ba+b Ca+b Dab 3(2 分)用加减法解方程组时,下列变形正确的是( ) A B C D 4(2 分)我县人口约为 530060 人,用科学记数法可表示为( ) A530061
2、0 人 B5.3006105人 C53104人 D0.53106人 5(2 分)一个正多边形的内角和为 540,则这个正多边形的每一个外角等于( ) A108 B90 C72 D60 6(2 分)如果 ab5,那么代数式(2)的值是( ) A B C5 D5 7(2 分)如图,排球运动员站在点 O 处练习发球,将球从 O 点正上方 2m 的 A 处发出,把球看成点,其运行的高度 y(m)与运行的水平距离 x(m)满足关系式 ya(xk)2+h已知球与 O 点的水平距离为6m 时,达到最高 2.6m,球网与 O 点的水平距离为 9m高度为 2.43m,球场的边界距 O 点的水平距离为18m,则下
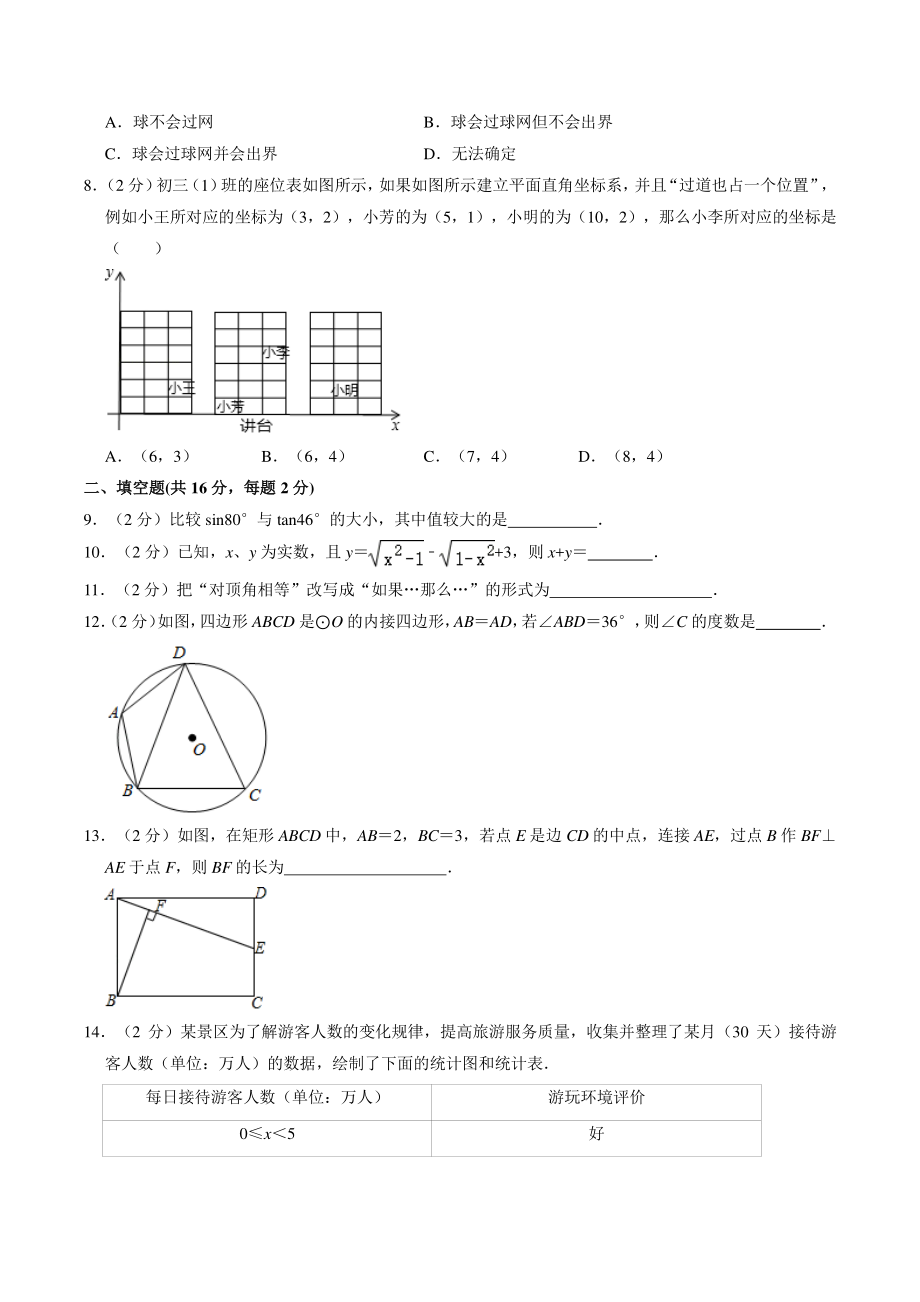
3、列判断正确的是( ) A球不会过网 B球会过球网但不会出界 C球会过球网并会出界 D无法确定 8 (2 分) 初三 (1) 班的座位表如图所示, 如果如图所示建立平面直角坐标系, 并且 “过道也占一个位置” ,例如小王所对应的坐标为(3,2),小芳的为(5,1),小明的为(10,2),那么小李所对应的坐标是( ) A(6,3) B(6,4) C(7,4) D(8,4) 二、填空题二、填空题(共共 16 分,每题分,每题 2 分分) 9(2 分)比较 sin80与 tan46的大小,其中值较大的是 10(2 分)已知,x、y 为实数,且 y+3,则 x+y 11(2 分)把“对顶角相等”改写成“
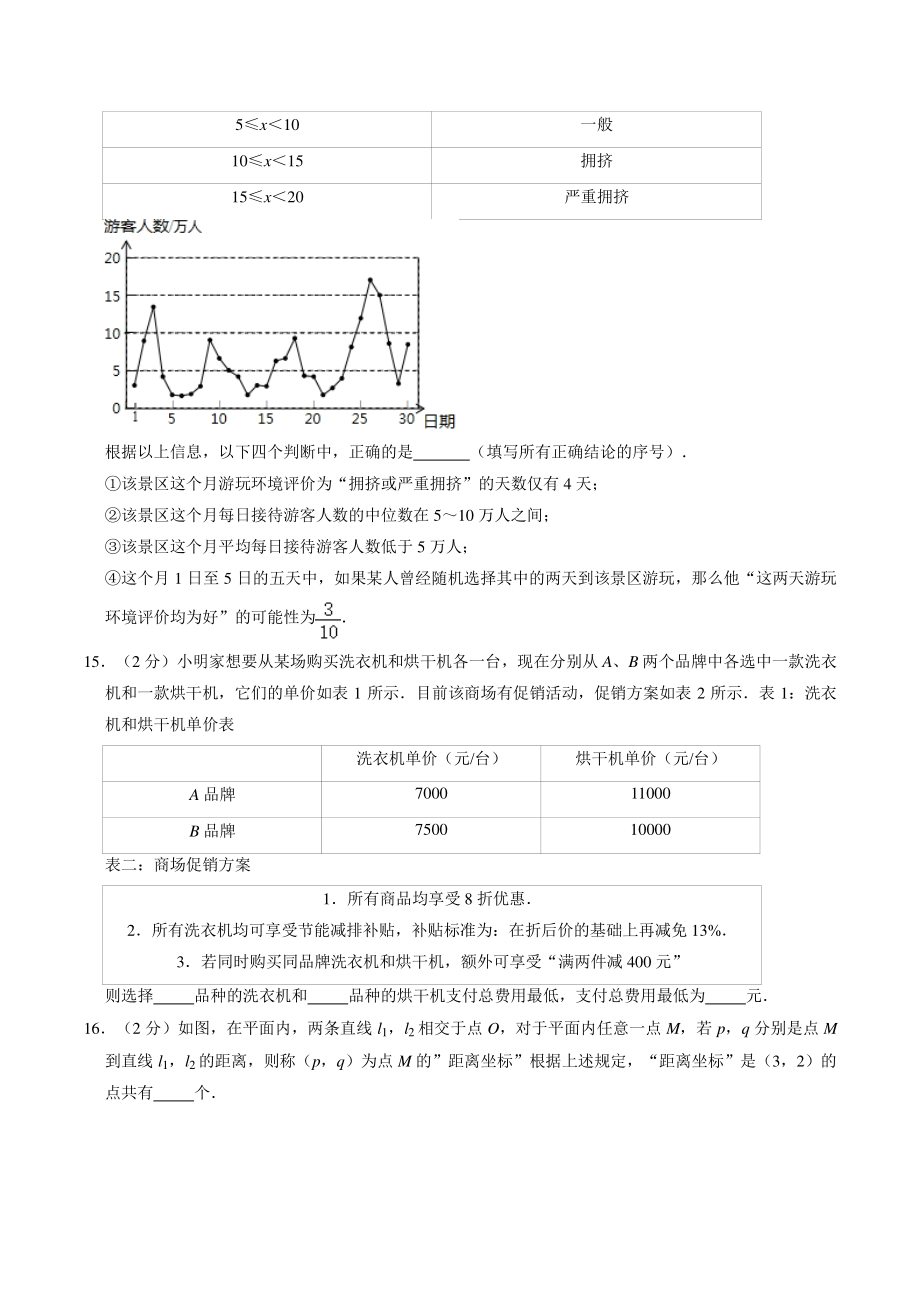
4、如果那么”的形式为 12(2 分) 如图, 四边形 ABCD 是O 的内接四边形, ABAD, 若ABD36, 则C 的度数是 13(2 分)如图,在矩形 ABCD 中,AB2,BC3,若点 E 是边 CD 的中点,连接 AE,过点 B 作 BFAE 于点 F,则 BF 的长为 14(2 分)某景区为了解游客人数的变化规律,提高旅游服务质量,收集并整理了某月(30 天)接待游客人数(单位:万人)的数据,绘制了下面的统计图和统计表 每日接待游客人数(单位:万人) 游玩环境评价 0 x5 好 5x10 一般 10 x15 拥挤 15x20 严重拥挤 根据以上信息,以下四个判断中,正确的是 (填写所
5、有正确结论的序号) 该景区这个月游玩环境评价为“拥挤或严重拥挤”的天数仅有 4 天; 该景区这个月每日接待游客人数的中位数在 510 万人之间; 该景区这个月平均每日接待游客人数低于 5 万人; 这个月 1 日至 5 日的五天中,如果某人曾经随机选择其中的两天到该景区游玩,那么他“这两天游玩环境评价均为好”的可能性为 15(2 分)小明家想要从某场购买洗衣机和烘干机各一台,现在分别从 A、B 两个品牌中各选中一款洗衣机和一款烘干机,它们的单价如表 1 所示目前该商场有促销活动,促销方案如表 2 所示表 1:洗衣机和烘干机单价表 洗衣机单价(元/台) 烘干机单价(元/台) A 品牌 7000 1
6、1000 B 品牌 7500 10000 表二:商场促销方案 1所有商品均享受 8 折优惠 2所有洗衣机均可享受节能减排补贴,补贴标准为:在折后价的基础上再减免 13% 3若同时购买同品牌洗衣机和烘干机,额外可享受“满两件减 400 元” 则选择 品种的洗衣机和 品种的烘干机支付总费用最低,支付总费用最低为 元 16(2 分)如图,在平面内,两条直线 l1,l2相交于点 O,对于平面内任意一点 M,若 p,q 分别是点 M到直线 l1,l2的距离,则称(p,q)为点 M 的”距离坐标”根据上述规定,“距离坐标”是(3,2)的点共有 个 三、解答题(共三、解答题(共 68 分,第分,第 17-2
7、0 题,每题题,每题 5 分,第分,第 21-22 题,每题题,每题 6 分,第分,第 23 题题 5 分,第分,第 24 题题 6 分,第分,第25 题题 5 分,第分,第 26 题题 6 分,第分,第 27-28 题,每题题,每题 7 分)解答应写出文字说明、演算步骤或证明过程。分)解答应写出文字说明、演算步骤或证明过程。 17(5 分)已知:如图,MON 为锐角,点 A 在射线 OM 上求作:射线 AC,使得 ACON 小静的作图思路如下: 以点 A 为圆心,AO 为半径作弧,交射线 ON 于点 B,连接 AB; 作MAB 的角平分线 AC 射线 AC 即为所求的射线 (1)使用直尺和圆
8、规,按照小静的作图思路补全图形(保留作图痕迹); (2)完成下面的证明 证明:OAAB, OABO( ) MAB 是AOB 的一个外角, MAB + ABOMAB AC 平分MAB, BACMAB ABOBAC ACON( ) 18(5 分)计算:(2)0+|1|+2cos30 19(5 分)解不等式组: 20(5 分)已知:关于 x 的方程 mx2+(m3)x30(m0) (1)求证:方程总有两个实数根; (2)如果 m 为正整数,且方程的两个根均为整数,求 m 的值 21(5 分)已知:如图,在ABC 中,直线 PQ 垂直平分 AC,与边 AB 交于点 E,连接 CE,过点 C 作CFBA
9、 交 PQ 于点 F,连接 AF (1)求证:四边形 AECF 是菱形; (2)若 AD3,AE5,则求菱形 AECF 的面积 22(5 分)如图,AB 是O 直径,点 C 在O 上,AD 平分CAB,BD 是O 的切线,AD 与 BC 相交于点 E,与O 相交于点 F,连接 BF (1)求证:BDBE; (2)若 DE2,BD2,求 AE 的长 23(6 分)如图,直线 yx+2 与反比例函数 y(x0)的图象交于点 A(2,m),与 y 轴交于点 B (1)求反比例函数的解析式; (2)连接 OA,将ABO 沿射线 BA 方向平移,平移后 A、O、B 的对应点分别为 A,O,B,当点 O恰
10、好落在反比例函数 y(x0)的图象上时,求点 O的坐标; (3)设点 P(0,n)过点 P 作平行于 x 轴的直线与直线 yx+2 和反比例函数 y(x0)的图象分别交于点 C,D,当 CD4 时,直接写出 n 的取值范围 24(6 分)如图 1,A,C 是平面内的两个定点,BAC30,P 为射线 AB 上一动点,过点 P 作 PC 的垂线交直线 AC 于点 D设APC 的度数为 x,PDC 的度数为 y小贤对 x 与 y 之间满足的等量关系进行了探究下面是小贤的探究过程,请补充完整: (1)如图 2,当 x35 时,依题意补全图形 (2)按照表中 x 的值进行取点、画图、计算,分别得到了 y
11、 与 x 的几组对应值,补全表格 x 30 40 80 90 y (3)如图 3 所示的是平面直角坐标系 xOy, 通过描出表中各组数值所对应的点(x,y),画出 y 与 x 的函数图象 结合中的图象填空,当 y50 时,x 的值为 (4)y 关于 x 的函数表达式为 (需写出自变量 x 的取值范围) 25(6 分)某市教育局为了了解初二学生每学期参加综合实践活动的情况,随机抽样调查了某校初二学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图请你根据图中提供的信息,回答下列问题: (1)扇形统计图中 a 的值为 ; (2)补全频数分布直方图; (3)在这次抽样调查中
12、,众数是 天,中位数是 天; (4)请你估计该市初二学生每学期参加综合实践活动的平均天数约是多少?(结果保留整数) 26(6 分)在平面直角坐标系 xOy 中,抛物线 ymx2+(m3)x3(m0)与 x 轴交于 A、B 两点(点A 在点 B 左侧),与 y 轴交于点 C,AB4,点 D 为抛物线的顶点 (1)求点 A 和顶点 D 的坐标; (2)将点 D 向左平移 4 个单位长度,得到点 E,求直线 BE 的表达式; (3)若抛物线 yax26 与线段 DE 恰有一个公共点,结合函数图象,求 a 的取值范围 27(7 分)如图,在正方形 ABCD 中,点 E 为线段 BC 上一动点(点 E
13、不与点 B、C 重合),点 B 关于直线 AE 的对称点为 F,作射线 EF 交 CD 于 H,连接 AF (1)求证:AFEH; (2)连接 AH,小王通过观察、实验,提出猜想:点 E 在运动过程中,EAH 的度数始终保持不变你帮助小王求出EAH 的度数 28(7 分)如图,在矩形 ABCD 中,AB6,BC8,O 是 AD 的中点,以 O 为圆心在 AD 的下方作半径为 3 的半圆 O,交 AD 于 E、F 思考:连接 BD,交半圆 O 于 G、H,求 GH 的长; 探究:将线段 AF 连带半圆 O 绕点 A 顺时针旋转,得到半圆 O,设其直径为 EF,旋转角为 (0180) (1)设 F
14、到 AD 的距离为 m,当 m时,求 的取值范围; (2)若半圆 O与线段 AB、BC 相切时,设切点为 R,求的长 (sin49,cos41,tan37,结果保留 ) 2022 年年北京市北京市中考中考模拟模拟数学试题(数学试题(3) 一、选择题一、选择题(共共 16 分,每题分,每题 2 分分)第第 1-8 题均有四个选项,符合题意的选项只有一个。题均有四个选项,符合题意的选项只有一个。 1(2 分)下列几何体中,其面既有平面又有曲面的有( ) A1 个 B2 个 C3 个 D4 个 【答案】B 【解析】球只有 1 个曲面;圆锥既有曲面又有平面;正方体只有平面;圆柱既有平面又有曲面; 故选
15、:B 2(2 分)实数 a、b 在数轴上的位置如图,则化简|a|+|b|的结果为( ) Aab Ba+b Ca+b Dab 【答案】C 【解析】由图可知,a0,b0, 所以,|a|+|b|a+b 故选:C 3(2 分)用加减法解方程组时,下列变形正确的是( ) A B C D 【答案】B 【解析】用加减法解方程组时,变形为:, 故选:B 4(2 分)我县人口约为 530060 人,用科学记数法可表示为( ) A5300610 人 B5.3006105人 C53104人 D0.53106人 【答案】B 【解析】530060 是 6 位数, 10 的指数应是 5, 故选:B 5(2 分)一个正多边
16、形的内角和为 540,则这个正多边形的每一个外角等于( ) A108 B90 C72 D60 【答案】C 【解析】设此多边形为 n 边形, 根据题意得:180(n2)540, 解得:n5, 这个正多边形的每一个外角等于:72 故选:C 6(2 分)如果 ab5,那么代数式(2)的值是( ) A B C5 D5 【答案】D 【解析】ab5, 原式ab5, 故选:D 7(2 分)如图,排球运动员站在点 O 处练习发球,将球从 O 点正上方 2m 的 A 处发出,把球看成点,其运行的高度 y(m)与运行的水平距离 x(m)满足关系式 ya(xk)2+h已知球与 O 点的水平距离为6m 时,达到最高
17、2.6m,球网与 O 点的水平距离为 9m高度为 2.43m,球场的边界距 O 点的水平距离为18m,则下列判断正确的是( ) A球不会过网 B球会过球网但不会出界 C球会过球网并会出界 D无法确定 【答案】C 【解析】球与 O 点的水平距离为 6m 时,达到最高 2.6m, 抛物线为 ya(x6)2+2.6 过点, 抛物线 ya(x6)2+2.6 过点(0,2), 2a(06)2+2.6, 解得:a, 故 y 与 x 的关系式为:y(x6)2+2.6, 当 x9 时,y(x6)2+2.62.452.43, 所以球能过球网; 当 y0 时,(x6)2+2.60, 解得:x16+218,x262
18、(舍去) 故会出界 故选:C 8 (2 分) 初三 (1) 班的座位表如图所示, 如果如图所示建立平面直角坐标系, 并且 “过道也占一个位置” ,例如小王所对应的坐标为(3,2),小芳的为(5,1),小明的为(10,2),那么小李所对应的坐标是( ) A(6,3) B(6,4) C(7,4) D(8,4) 【答案】C 【解析】根据题意知小李所对应的坐标是(7,4), 故选:C 二、填空题二、填空题(共共 16 分,每题分,每题 2 分分) 9(2 分)比较 sin80与 tan46的大小,其中值较大的是_ 【答案】tan46 【解析】sin 随 的增大而增大,且 sin80sin90, sin
19、801, tan 随 的增大而增大,且 tan46tan45, tan461, 则 tan46sin80, 10(2 分)已知,x、y 为实数,且 y+3,则 x+y_ 【答案】2 或 4 【解析】由题意知,x210 且 1x20, 所以 x1 所以 y3 所以 x+y2 或 4 11(2 分)把“对顶角相等”改写成“如果那么”的形式为_ 【答案】如果两个角是对顶角,那么这两个角相等 【解析】把“对顶角相等”改写成“如果那么”的形式为:如果两个角是对顶角,那么这两个角相等, 12(2 分) 如图, 四边形 ABCD 是O 的内接四边形, ABAD, 若ABD36, 则C 的度数是_ 【答案】7
20、2 【解析】ABAD,ABD36, ADBABD36, A180ADBABD108, 四边形 ABCD 是O 的内接四边形, C+A180, C18010872, 13(2 分)如图,在矩形 ABCD 中,AB2,BC3,若点 E 是边 CD 的中点,连接 AE,过点 B 作 BFAE 于点 F,则 BF 的长为_ 【答案】 【解析】在矩形 ABCD 中,CDAB2,ADBC3,BADD90, E 是边 CD 的中点, DECD1, AE, BFAE, BAE+DAEDAE+AED90, BAEAED, ABFAED, , , BF 14(2 分)某景区为了解游客人数的变化规律,提高旅游服务质

- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2022 北京市 中考 模拟 数学试卷 答案 解析
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
文档标签
- 数学试卷
- 2022年北京市中考模拟数学试卷3含答案解析
- 2022年北京市中考模拟数学试卷1含答案解析
- 2022年北京市中考模拟数学试卷2含答案解析
- 2022年北京市中考仿真数学试卷3含答案解析
- 2022年北京市昌平区中考模拟数学试卷1含答案解析
- 2022年北京市昌平区中考模拟数学试卷2含答案解析
- 2022年北京市朝阳区中考模拟数学试卷3含答案解析
- 2022年北京市中考学业水平模拟数学试卷含答案
- 2022北京专家
- 2022年北京市中考数学押题预测模拟试卷含答案解析
- 2022年北京初
- 2022年北京市中考模拟数学试卷含答案解析
- 2022年北京市中考模拟数学试卷5含答案解析
- 2022年北京市顺义中考模拟语文试卷含答案
- 2022年模拟数学试卷含答案
- 2022北京数学
- 2022年北京市生物试卷含答案
- 2022版北京中考数学
- 2022年北京中考数学



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-209195.html