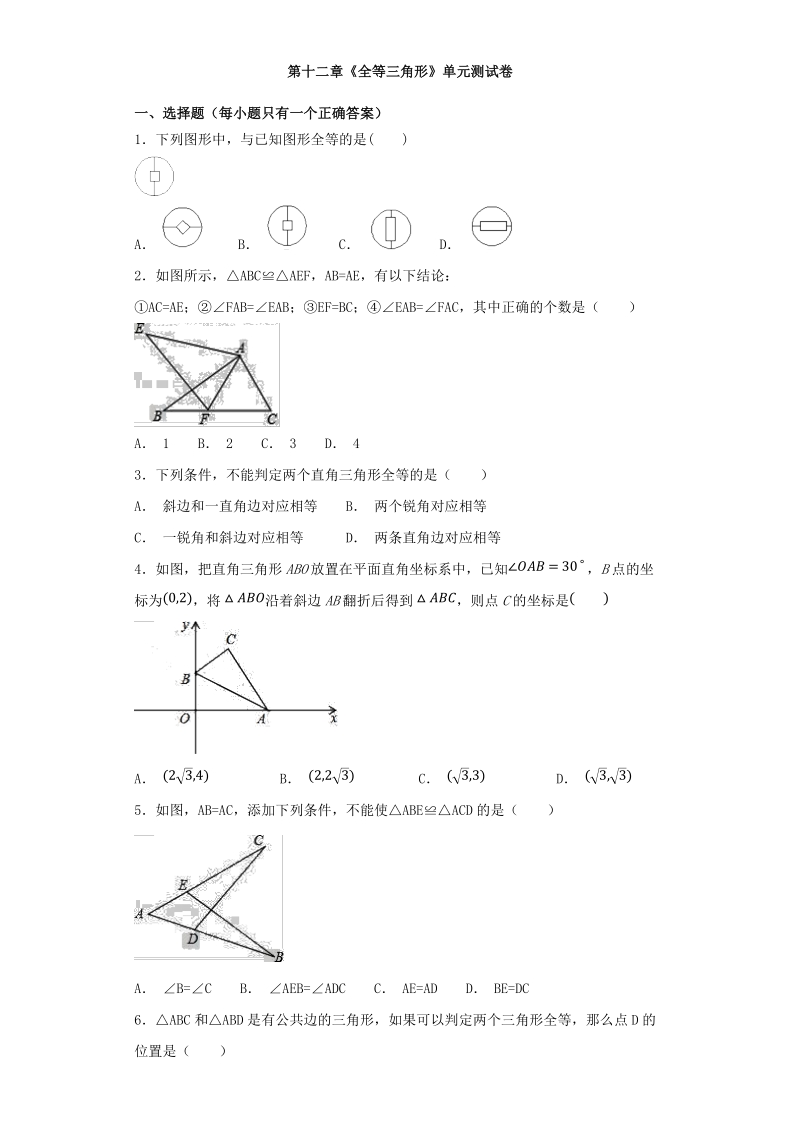
1、第十二章全等三角形单元测试卷一、选择题（每小题只有一个正确答案）1下列图形中，与已知图形全等的是( )A B C D 2如图所示，ABCAEF，AB=AE，有以下结论：AC=AE；FAB=EAB；EF=BC；EAB=FAC，其中正确的个数是（ ）A 1 B 2 C 3 D 4 3下列条件，不能判定两个直角三角形全等的是（ ）A 斜边和一直角边对应相等 B 两个锐角对应相等C 一锐角和斜边对应相等 D 两条直角边对应相等4如图，把直角三角形 ABO 放置在平面直角坐标系中，已知 ， B 点的坐=30标为 ，将 沿着斜边 AB 翻折后得到 ，则点 C 的坐标是 (0,2) ( )A B C D (
2、23,4) (2,23) ( 3,3) ( 3, 3)5如图，AB=AC，添加下列条件，不能使ABEACD 的是（ ）A B=C B AEB=ADC C AE=AD D BE=DC6ABC 和ABD 是有公共边的三角形，如果可以判定两个三角形全等，那么点 D 的位置是（ ）试卷第 2 页，总 6 页A 是唯一确定的 B 有且只有两种可能C 有且只有三种可能 D 有无数种可能7如图，在ABC 中，ABC=45，AD，BE 分别为 BC、AC 边上的高，AD、BE 相交于点 F，连接 CF，则下列结论，BF=AC；FCD=45；若 BF=2EC，则FDC 周长等于 AB 的长；若FBD=30，BF
3、=2，则 AF= 1其中正确的有（ ）3A 1 个 B 2 个 C 3 个 D 4 个8一块三角形玻璃板不慎被小强同学碰破,成了如图所示的四块,聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃板,你认为可行的方案是( )A 带其中的任意两块去都可以 B 带、或、去就可以了C 带、或、去就可以了 D 带、或、去就可以了9如图，OP 平分 ， 于点 A，点 Q 是射线 OM 上一个动点，若 ，则 =3PQ 的最小值为 ( )A B 2 C 3 D 41.510如图是由 4 个相同的小正方形组成的网格图，其中 等于 1+2 ( )A B C D 150 18
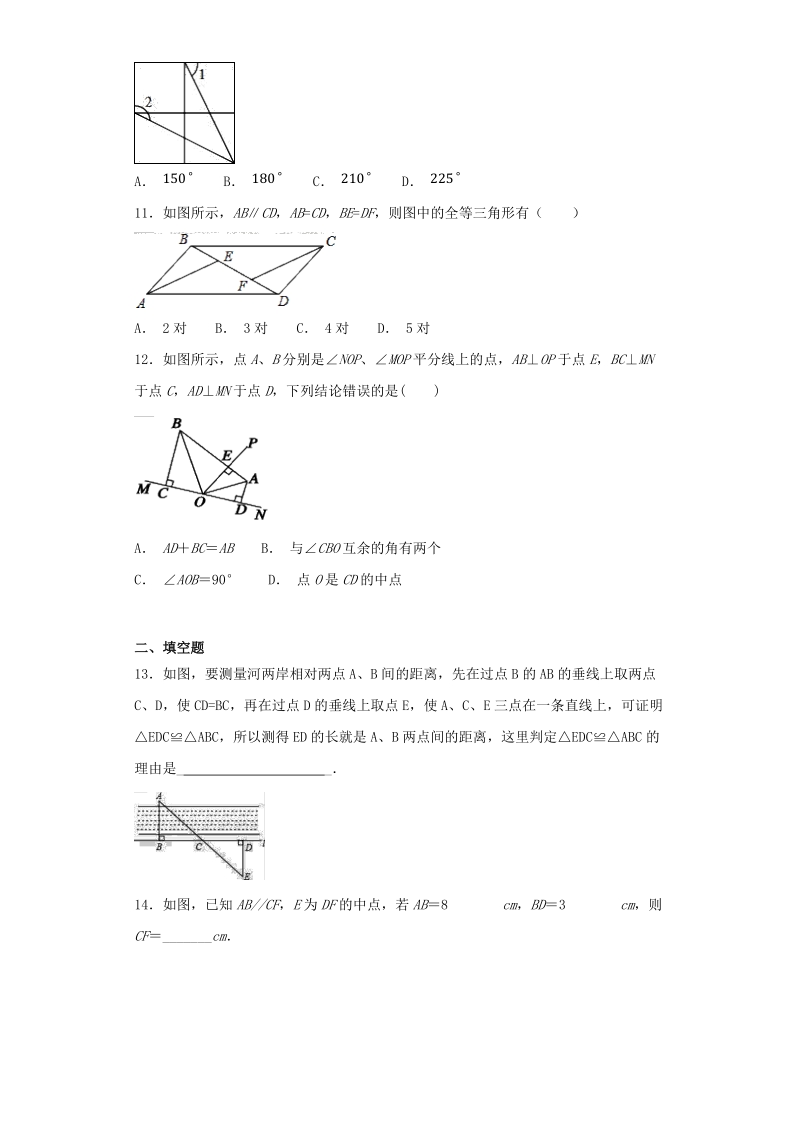
4、0 210 22511如图所示， AB CD， AB=CD， BE=DF，则图中的全等三角形有（ ）A 2 对 B 3 对 C 4 对 D 5 对12如图所示，点 A、 B 分别是 NOP、 MOP 平分线上的点， AB OP 于点 E， BC MN于点 C， AD MN 于点 D，下列结论错误的是( )A AD BC AB B 与 CBO 互余的角有两个C AOB90 D 点 O 是 CD 的中点二、填空题13如图，要测量河两岸相对两点 A、B 间的距离，先在过点 B 的 AB 的垂线上取两点C、D，使 CD=BC，再在过点 D 的垂线上取点 E，使 A、C、E 三点在一条直线上，可证明ED
5、CABC，所以测得 ED 的长就是 A、B 两点间的距离，这里判定EDCABC 的理由是_ _14如图，已知 AB/CF， E 为 DF 的中点，若 AB8 cm， BD3 cm，则CF_ cm试卷第 4 页，总 6 页15如图，在四边形 ABCD 中， AB=CD， AD=BC，对角线 AC、 BD 交于点 O，则图中共有全等三角形_对16如图，ABCADE，BC 的延长线过点 E，ACB=AED=105，CAD=10，B=50，则DEF 的度数为_.17如图，OAOB，OCOD，O50，D35，则AEC_三、解答题18如图，在ABC 中，AB=AC，1=2，则ABD 与ACD 全等吗？证明
6、你的判断19如图，在ABE 中，C 为边 AB 延长线上一点，BC=AE，点 D 在EBC 内部，且EBD=A=DCB（1）求证：ABECDB（2）连结 DE，若CDB=60，AEB=50，求BDE 的度数20如图，已知点 B、D、E、C 四点在一条直线上，且ABEACD求证（1）BD=CE； （2）ABDACE21已知：如图所示ACB 和DCE 都是等腰直角三角形，ACB=DCE=90，连接AE，BD求证：AE=BD22如图，AD 是ABC 的角平分线，DEAB，DFAC，垂足分别是 E，F，连接 EF，EF与 AD 相交于点 G求证：AD 是 EF 的垂直平分线23阅读下列材料：已知：如图
7、 1，直线 AB CD，点 E 是 AB、 CD 之间的一点，连接 BE、 DE 得到 BED 求证： BED = B+ D.图 1小冰是这样做的：证明：过点 E 作 EF AB，则有 BEF= B AB CD， EF CD FED= D BEF + FED = B+ D 试卷第 6 页，总 6 页即 BED= B+ D请利用材料中的结论，完成下面的问题：已知：直线 AB CD，直线 MN 分别与 AB、 CD 交于点 E、 F（1）如图 2， BEF 和 EFD 的平分线交于点 G猜想 G 的度数，并证明你的猜想；（2）如图 3， EG1和 EG2为 BEF 内满足1=2 的两条线，分别与
8、EFD 的平分线交于点 G1和 G2求证： FG1 E+ G2=180 参考答案1B【解析】【分析】根据全等图形的定义:能够完全重合的两个图形是全等图形.【详解】根据全等图形的定义可得:B 选项中图形能够与已知图形完全重合,故选 B.【点睛】本题主要考查全等图形的定义,解决本题的关键是要熟练掌握全等图形的定义.2B【解析】【分析】因ABCAEF，AB=AE，根据全等三角形的性质即可解答.【详解】ABCAEF，AB=AE， EF=BC，EAF=BAC， （故正确）EAB+BAF=FAC+BAF，即EAB=FAC， （故正确）AC 与 AE 不是对应边，不能求出二者相等，也不能求出FAB=EAB，
9、故、错误.故选 B【点睛】本题考查的是全等三角形的性质，解题时要运用三角形全等的基本性质结合图形进行思考3B【解析】【分析】根据全等三角形的判定方法逐一验证即可.【详解】A.正确，符合判定 HL，故选项错误；B.错误，全等三角形的判定必须有边的参与，故选项正确；C.正确，符合判定 AAS，故选项错误；D.正确，符合判定 SAS，故选项错误.故选 B.【点睛】本题考查全等三角形的判定，熟练掌握各个全等三角形判定的方法是解此题的关键.4C【解析】【分析】过点 C 作 CDy 轴，垂直为 D，首先证明BOABCA，从而可求得 BC 的长，然后再求得DCB=30，接下来，依据在 RtBCD 中，求得
10、BD、DC 的长，从而可得到点 C 的坐标【详解】， ， ，=30 =90 = ， ，=2 =60过点 C 作 轴，垂直为 D，则 ， =30， ，=12=1 =32=3，( 3,3)故选 C【点睛】本题考查了全等三角形的性质和判定、含 30角的直角三角形的性质，正确添加辅助线、熟练掌握和灵活运用相关知识是解题的关键5D【解析】【分析】已知 AB=AC，A 是公共角，根据选项逐一进行分析即可得.【详解】A、添加B=C 可利用 ASA 证明ABEACD，故此选项不合题意；B、添加AEB=ADC 可利用 AAS 证明ABEACD，故此选项不合题意；C、添加 AE=AD 可利用 SAS 证明ABEA
11、CD，故此选项不合题意；D、添加 EB=DC 不能证明ABEACD，故此选项符合题意，故选 D【点睛】本题考查了全等三角形的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL注意：AAA、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角6C【解析】【分析】根据题意可知，ABC 和ABD 有公共边 AB，当 C、D 在 AB 的同侧时，画出图形，如图所示，可得ABCBAD；再画出 C、D 在 AB 的异侧的图形，即可确定答案.【详解】如图所示，ABCBADABDBAD，即点 D 的位置有且只有三种可能.【
12、点睛】本题重点考查了三角形全等的判定定理，正确画出 C、D 在 AB 同侧和异侧的图形是解答本题的关键7D【解析】【分析】想办法证明ADCBDF 即可一一判断.【详解】ABC 中，AD，BE 分别为 BC、AC 边上的高，ABC=45，AD=BD，DAC 和FBD 都是ACD 的余角，而ADB=ADC=90，BDFADC，BF=AC，故正确，FD=CD，FCD=CFD=45，故正确；若 BF=2EC，根据得 BF=AC，AC=2EC，即 E 为 AC 的中点，BE 为线段 AC 的垂直平分线，AF=CF，BA=BC，AB=BD+CD=AD+CD=AF+DF+CD=CF+DF+CD，即FDC 周
13、长等于 AB 的长，故正确FBD=30，BF=2，DF=1，BD=AD= ，3AF= 1，故正确，3故选：D【点睛】此题考查了全等三角形的性质与判定，也考查了线段的垂直平分线的性质与判定，也利用了三角形的周长公式解题，综合性比较强，对学生的能力要求比较高8C【解析】 【分析】、或、只能得到原三角形的一个角，没有边，因此确定不了；、虽然可以得到两个角，但没有边，因此确定不了；带、可以用“角边角”确定三角形；带、也可以用“角边角”确定三角形【详解】带、可以用“角边角”确定三角形，带、可以用“角边角”确定三角形，带、或、或、确定不了三角形，故选 C【点睛】本题考查了全等三角形判定的应用；确定一个三角
14、形的大小、形状，可以用全等三角形的几种判定方法，做题时要根据实际问题找条件9C【解析】【分析】根据角平分线的性质结合点到直线垂线段最短，即可得出 ，此题得解【详解】解： 平分 ， 于点 A， ， =3=3故选：C【点睛】本题考查了角平分线的性质以及垂线段最短，根据角平分线的性质结合垂线段最短，求出PQ 的最小值是解题的关键10B【解析】【分析】根据 SAS 可证得 ，可得出 ，继而可得出答案，再根据邻补角 =的定义求解.【详解】由题意得： ， ， ，=90 ，=1+2=180故选：B【点睛】本题考查全等图形的知识，比较简单，解答本题的关键是判断出 .11B【解析】 【分析】：根据平行线的性质得
15、出ABE=CDF，根据 SAS 推出ABECDF，AEDCFB，推出 BC=AD，根据 SSS 推出ABDCDB 即可【详解】因为 ABCD ，所以ABE=CDF，又因为 AB=CD， BE=DF，所以ABECDF（SAS）所以AEB=CFD,AE=CE所以，AED=CFB,由因为 BF=DE，所以AEDCFB(SAS)所以 BC=AD,由 AB=CD,BF=DE,所以ABDCDB（SSS）所以图中有 3 对全等三角形，是ABDCDB，ABECDF，ADECBF，故正确选项为：B【点睛】本题考查了全等三角形的性质和判定的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS;全等三角
16、形的对应边相等，对应角相等12B【解析】【分析】根据角平分线上的点到角的两边距离相等可得 AD=AE， BC=BE，利用角平分线的定义和平角的性质可得到 AOB 的度数，再利用“HL”证明 Rt AOD 和 Rt AOE 全等，根据全等三角形对应边相等可得 OD=OE，同理可得 OC=OE，然后求出 AOB=90，然后对各选项分析判断即可得解【详解】点 A， B 分别是 NOP， MOP 平分线上的点， AD=AE， BC=BE AB=AE+BE， AB=AD+BC，故 A 选项结论正确；与 CBO 互余的角有 COB， EOB， OAD， OAE 共 4 个，故 B 选项结论错误；点 A、
17、B 分别是 NOP、 MOP 平分线上的点， AOE= EOD， BOC= MOE， AOB=12 12( EOD+ MOE)= 180=90，故 C 选项结论正确；12 12在 Rt AOD 和 Rt AOE 中， ，Rt AODRt AOE（HL） ， OD=OE，同理可得= OC=OE， OC=OD=OE，点 O 是 CD 的中点，故 D 选项结论正确故选 B【点睛】本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，余角的定义，熟记各性质并准确识图是解题的关键13ASA 【解析】【分析】根据已知条件分析，题目中给出了三角形的边相等，两条垂线，可得一对角相等，加上图
18、形中的对顶角相等，条件满足了 ASA，答案可得【详解】ABBD，EDBD，ABD=EDC=90，在EDC 和ABC 中，= EDCABC（ASA） ，DE=AB，故答案为：ASA【点睛】本题考查了全等三角形的应用，熟练掌握全等三角形的判定与性质是解题的关键.145【解析】【分析】根据平行线的性质求得内错角相等，已知对顶角相等，又知 E 是 DF 的中点，所以根据 ASA得出ADECFE，从而得出 AD=CF，已知 AB，BD 的长，那么 CF 的长就不难求出【详解】 AB FC， ADE= EFC， E 是 DF 的中点， DE=EF，在 ADE 与 CFE 中，=， ADE CFE， AD=
19、CF， AB=8cm， BD=3cm， AD=ABBD=83=5cm， CF=AD=5cm，故答案为:5.【点睛】考查平行线的性质，全等三角形的判定与性质，掌握全等三角形的判定方法是解题的关键.154【解析】解：在 ABD 和 CDB 中， ， ABD CDB（SSS） ，= ADB= CBD， ABD= BDC在 ABC 和 CDA 中， ， ABC CDA（SSS ） ，= DAC= BCA， ACD= BAC在 AOB 和 COD 中， ， AOB COD（ASA） = 在 AOD 和 COB 中， ， AOD COB（ASA） 故答案为：4= 点睛：本题主要考查了全等三角形的判定与性质
20、，关键是判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL注意： AAA、 SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角1635【解析】【分析】由ABCADE，得D=B=50，故EAD=25，可得EAC=CAD+EAD =35.由ACB=105，得AEF=70，可求DEF=35.【详解】ABCADE，D=B=50.AED=105，EAD=25，EAC=CAD+EAD =35.ACB=105，AEF=70，DEF=35.故答案为：35【点睛】本题主要考查全等三角形的对应角相等及三角形的外角的性质.熟记相关性质是
21、关键.1760【解析】【分析】本题需先证出 BOC AOD，求出 C，再求出 DAC，最后根据三角形的内角和定理即可求出答案【详解】在 BOC 和 AOD 中， OA=OB， O= O， OC=OD， BOCAOD， C= D=35 DAC= O+ D=50+35=85， AEC=180 DAC C=1808535=60故答案为：60【点睛】本题主要考查了全等三角形的判定和性质，在解题时要注意和三角形的内角和定理相结合是本题的关键18全等，见解析.【解析】【分析】全等，因为1=2，所以DBC 为等腰三角形，则 BD=CD，又因为 AB=AC，ADAD，通过“边边边”即可证得两个三角形全等.【详
22、解】解：ABD 与ACD 全等，1=2，BD=CD，在ABD 与ACD 中， ，= ABDACD（SSS） 【点睛】本题考查全等三角形的证明，方法不唯一，可以通过证明三条边对应相等来证明，也可以通过两边及夹角对应相等来证明.19(1)见解析；（2）55 o【解析】【分析】（1）利用ABE+EBD+DBC=180，A+AEB+EBA=180，的关系， 求出BDCEBA，再利用 AAS 证明ABECDB.( 2 )利用ABECDB，得出 BE=DB,即BEDBDE，再利用ABE+EBD+BDC180之间的关系求出EBD 的度数.【详解】证明：（1）ABE+EBD+DBC=180，A+AEB+EBA
23、=180，EBD=A=DCB，EBA=DBC，在ABE 与CDB 中 ，ABECDB（AAS） ，（2）ABECDB，BE=DB，AEB=DBC，CDB=60，AEB=50，DBC=50，C=1806050=70，EBD=DCB=70，BDE= 【点睛】本题考查了三角形外角的性质和全等三角形的性质和判定的应用，主要考查了学生的推理能力.20见解析.【解析】【分析】（1）根据全等三角形的性质可得 EB=DC，再根据等式的性质可得 BD=CE；（2）根据全等三角形的性质可得B=C，AB=AC，在加上（1）中的结论可利用 SAS 证明ABDACE【详解】（1）ABEACD，EB=DC，EBDE=DC
24、DE，即 DB=EC；（2）ABEACD，B=C，AB=AC，在ABD 和ACE 中，= ABDACE（SAS） 【点睛】本题考查了全等三角形的判定与性质，关键是掌握全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具在判定三角形全等时，关键是选择恰当的判定方法21详见解析.【解析】【分析】根据等腰直角三角形的性质得出ACB=DCE=90，AC=BC，DC=EC，然后加上同一个角得出BCD=ACE，从而说明ACE 和BCD 全等，从而得出答案【详解】证明：ACB 和DCE 都是等腰直角三角形，ACB=DCE=90，AC=BC，DC=EC，ACB+ACD=DCE+ACD，BCD=AC
25、E，在ACE 与BCD 中，ACEBCD（SAS） ，AE=BD【点睛】本题主要考查的是三角形全等的证明，属于基础题型找出隐含的条件以及明确等腰直角三角形的性质是解题的关键22证明见解析.【解析】【分析】根据角平分线上的点到角的两边的距离相等可得 DE=DF，然后利用“HL”证明 RtAED 和RtAFD 全等，根据全等三角形对应边相等可得 AE=AF，再根据线段垂直平分线的判定即可得.【详解】AD 是ABC 的角平分线，DEAB，DFAC，DE=DF，AED=AFD=90，在 RtAED 和 RtAFD 中，= RtAEDRtAFD，AE=AF，DE=DF，A、D 为不同的点，直线 AD 是
26、 EF 的垂直平分线，AD 垂直平分 EF【点睛】本题考查了角平分线上的性质、全等三角形的判定与性质、线段垂直平分线的判定，熟练掌握到线段两个端点距离相等的点在这条线段的垂直平分线上是解题的关键.23 （1）猜想： EGF=90证明见解析；（2）证明见解析.【解析】【分析】（1）如图 2 所示，猜想： EGF=90；由结论（1）得 EGF= BEG+ GFD，根据 EG、 FG分别平分 BEF 和 EFD，得到 BEF=2 BEG， EFD=2 GFD，由于 BE CF 到 BEF+ EFD=180，于是得到 2 BEG+2 GFD=180，即可得到结论；（2）如图 3，过点 G1作 G1H
27、AB 由结论（1）可得 G2=1+3， EG1F= BEG1+ G1FD，得到3= G2FD，由于 FG2平分 EFD 求得4= G2FD，由于1=2，于是得到 G2=2+4，由于 EG1F= BEG1+ G1FD，得到 EG1F+ G2=2+4+ BEG1+ G1FD= BEF+ EFD，然后根据平行线的性质即可得到结论【详解】（1）猜想： EGF=90 证明： EG， FG 分别平分 BEF 和 EFD， BEF =2 BEG， EFD=2 GFD BE/CF， BEF + EFD=180 2 BEG+2 GFD=180 BEG+ GFD=90 由小冰的结论可得 EGF = BEG+ GFD， EGF=90 （2）证明：过点 G1作 G1H/AB， AB/CD， G1H/CD 3= G2FD 由小冰的结论可得 G2 =1+3， FG2平分 EFD，4= G2FD 1=2， G2=2+4 由小冰的结论可得 EG1F = BEG1+ G1FD， EG1F + G2 = BEG1+ G1FD+2+4= BEF+ EFD=180【点睛】本题考查了平行线的性质，角平分线的性质，熟练掌握平行线的性质定理是解题的关键平行线的性质：两直线平行同位角相等;两直线平行内错角相等;两直线平行同旁内角互补
