 2021-2022学年内蒙古乌兰察布市部分旗九年级上期末数学试卷(含答案详解)
2021-2022学年内蒙古乌兰察布市部分旗九年级上期末数学试卷(含答案详解)
《2021-2022学年内蒙古乌兰察布市部分旗九年级上期末数学试卷(含答案详解)》由会员分享,可在线阅读,更多相关《2021-2022学年内蒙古乌兰察布市部分旗九年级上期末数学试卷(含答案详解)(17页珍藏版)》请在七七文库上搜索。
1、2021-2022 学年内蒙古乌兰察布市部分旗九年级学年内蒙古乌兰察布市部分旗九年级上期末数学试卷上期末数学试卷 一、选择题(每题一、选择题(每题 3 分,共分,共 36 分)分) 1 (3 分)在如图所示标志中,既是轴对称图形,又是中心对称图形的是( ) A B C D 2 (3 分)下列方程中,一元二次方程有( ) 3x2+x20;2x23xy+40;x21; A2 个 B3 个 C4 个 D5 个 3 (3 分)关于 x 的一元二次方程(m1)x2+5x+m23m+20,常数项为 0,则 m 值等于( ) A1 B2 C1 或 2 D0 4 (3 分)三角形的两边长分别为 3 和 6,第
2、三边的长是方程 x26x+80 的一个根,则这个三角形的周长是( ) A9 B11 C13 D14 5 (3 分)下列说法中正确的是( ) A “打开电视,正在播放新闻联播 ”是必然事件 B某次抽奖活动中奖的概率为,说明每买 100 张奖券,一定有一次中奖 C想了解台州市城镇居民人均年收入水平,宜采用抽样调查 D我市未来三天内肯定下雪 6 (3 分)将抛物线 y3x2向左平移 2 个单位,再向下平移 1 个单位,所得抛物线为( ) Ay3(x2)21 By3(x2)2+1 Cy3(x+2)21 Dy3(x+2)2+1 7 (3 分)如图,如果从半径为 9cm 的圆形纸片剪去圆周的一个扇形,将留
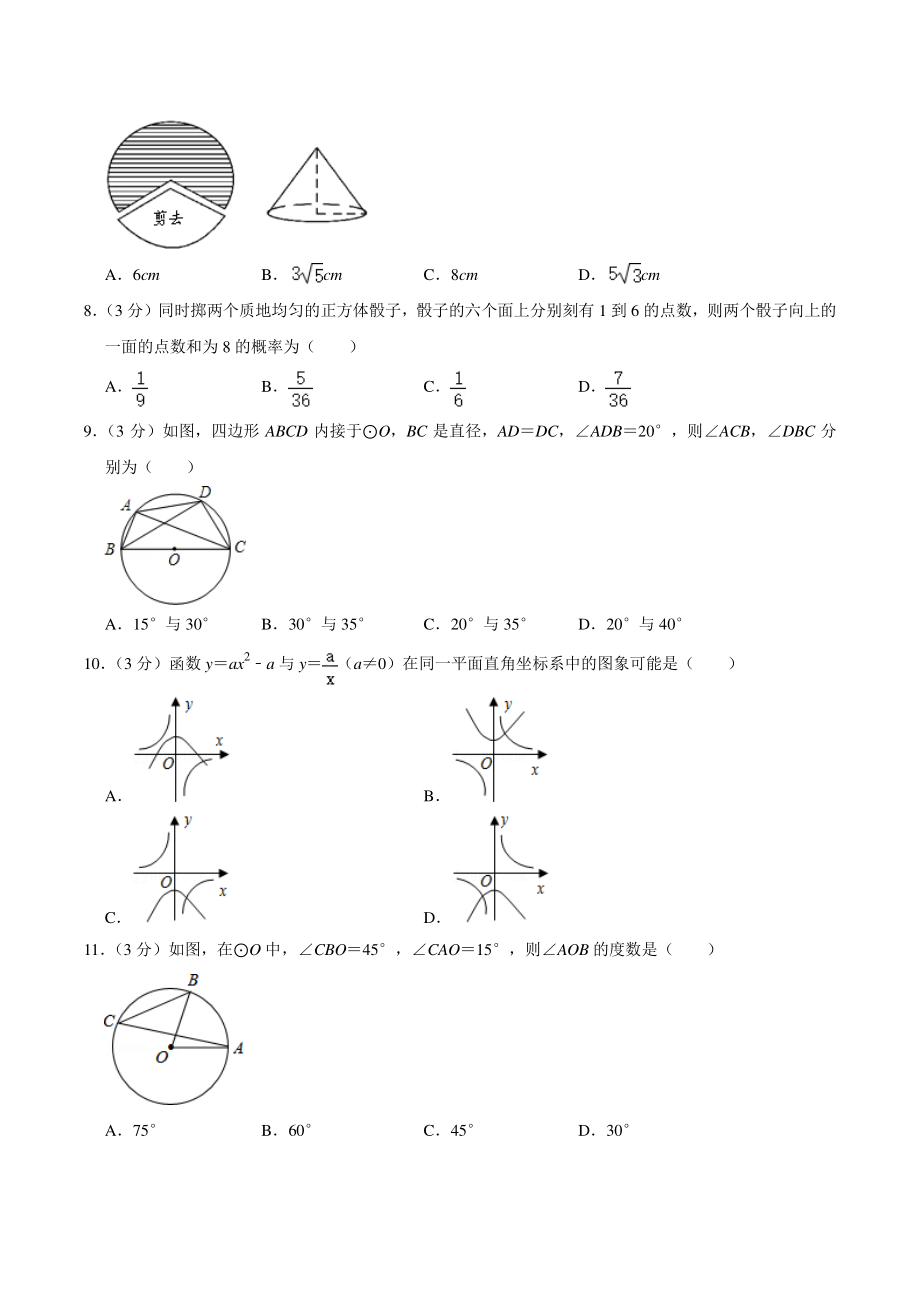
3、下的扇形围成一个圆锥(接缝处不重叠) ,那么这个圆锥的高为( ) A6cm Bcm C8cm Dcm 8 (3 分)同时掷两个质地均匀的正方体骰子,骰子的六个面上分别刻有 1 到 6 的点数,则两个骰子向上的一面的点数和为 8 的概率为( ) A B C D 9 (3 分)如图,四边形 ABCD 内接于O,BC 是直径,ADDC,ADB20,则ACB,DBC 分别为( ) A15与 30 B30与 35 C20与 35 D20与 40 10 (3 分)函数 yax2a 与 y(a0)在同一平面直角坐标系中的图象可能是( ) A B C D 11 (3 分)如图,在O 中,CBO45,CAO15
4、,则AOB 的度数是( ) A75 B60 C45 D30 12 (3 分)如图,二次函数 yax2+bx+c 的图象与 y 轴正半轴相交,其顶点的坐标为(,1) ,下列结论:c0;b24ac0;a+b0;4acb24a,其中错误的是( ) A B C D 二、填空题(每空二、填空题(每空 3 分,共分,共 24 分)分) 13 (3 分)如图,在 RtABC 中,ACB90,ABC30,将ABC 绕点 C 顺时针旋转至ABC,使得点 A恰好落在 AB 上,则旋转角度为 14 (3 分)关于 x 的方程 mx2+mx+10 有两个相等的实数根,那么 m 15 (3 分)一条弦把圆分为 2:3
5、两部分,那么这条弦所对的圆周角的度数为 16 (3 分)顶角为 120的等腰三角形腰长为 4cm,则它的外接圆的直径 cm 17 (3 分)在一元二次方程 ax2+bx+c0 中,若 a、b、c 满足关系式 ab+c0,则这个方程必有一个根为 18 (3 分)某小区 2012 年屋顶绿化面积为 2000 平方米,计划 2014 年屋顶绿化面积要达到 2880 平方米,如果每年屋顶绿化面积的增长率相同,那么这个增长率是 19 (6 分)如图,AB 是O 的直径,C 为圆上一点,A60,ODBC,D 为垂足,且 OD10,则AB ,BC 三、解答题(共三、解答题(共 60 分)分) 20 (10
6、分)解下列方程 (1) (x3) (x1)8; (2)2x2x10(用配方法解方程) 21 (10 分)如图,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘 A,B,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为 0 时,甲获胜;数字之和为 1 时,乙获胜如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止 (1)用画树状图或列表法求乙获胜的概率; (2)这个游戏规则对甲、乙双方公平吗?请判断并说明理由 22 (8 分)如图所示,PA、PB 是O 的切线,A、B 为切点,APB40,点 C 是O
7、上不同于 A、B的任意一点,求ACB 的度数 23 (8 分)如图,O 分别切ABC 的三条边 AB、BC、CA 于点 D、E、F、若 AB5,AC6,BC7,求 AD、BE、CF 的长 24 (12 分) 某商场销售一批名牌衬衫, 平均每天可售出 20 件, 每件盈利 40 元, 为了扩大销售, 增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价 1 元,商场平均每天可多售出 2 件求: (1)若商场平均每天要盈利 1200 元,每件衬衫应降价多少元? (2)每件衬衫降价多少元时,商场平均每天盈利最多? 25 (12 分)已知二次函数 yx22mx+m21 (
8、1)当二次函数的图象经过坐标原点 O(0,0)时,求二次函数的解析式; (2)如图,当 m2 时,该抛物线与 y 轴交于点 C,顶点为 D,求 C、D 两点的坐标; (3)在(2)的条件下,x 轴上是否存在一点 P,使得 PC+PD 最短?若 P 点存在,求出 P 点的坐标;若P 点不存在,请说明理由 参考答案与试题解析参考答案与试题解析 一、选择题(每题一、选择题(每题 3 分,共分,共 36 分)分) 1 (3 分)在如图所示标志中,既是轴对称图形,又是中心对称图形的是( ) A B C D 【解答】解:A是轴对称图形,不是中心对称图形,故此选项不合题意; B既是中心对称图形,也是轴对称图
9、形,符合题意; C是中心对称图形,不是轴对称图形,故此选项不合题意; D不是轴对称图形,也不是中心对称图形,故此选项不合题意 故选:B 2 (3 分)下列方程中,一元二次方程有( ) 3x2+x20;2x23xy+40;x21; A2 个 B3 个 C4 个 D5 个 【解答】解:符合一元二次方程定义,正确; 方程含有两个未知数,错误; 不是整式方程,错误; 符合一元二次方程定义,正确; 符合一元二次方程定义,正确 故选:B 3 (3 分)关于 x 的一元二次方程(m1)x2+5x+m23m+20,常数项为 0,则 m 值等于( ) A1 B2 C1 或 2 D0 【解答】解:关于 x 的一元
10、二次方程(m1)x2+5x+m23m+20,常数项为 0, , 解得:m2 故选:B 4 (3 分)三角形的两边长分别为 3 和 6,第三边的长是方程 x26x+80 的一个根,则这个三角形的周长是( ) A9 B11 C13 D14 【解答】解:解方程 x26x+80 得, x2 或 4, 第三边长为 2 或 4 当第三边为 2 时, 2+36, 边长为 2,3,6 不能构成三角形; 当第三边为 4 时, 3+46, 边长为 3,4,6 能构成三角形; 三角形的周长为 3+4+613, 故选:C 5 (3 分)下列说法中正确的是( ) A “打开电视,正在播放新闻联播 ”是必然事件 B某次抽
11、奖活动中奖的概率为,说明每买 100 张奖券,一定有一次中奖 C想了解台州市城镇居民人均年收入水平,宜采用抽样调查 D我市未来三天内肯定下雪 【解答】解:A、 “打开电视,正在播放新闻联播 ”是随机事件,故此选项错误; B、某次抽奖活动中奖的概率为,说明每买 100 张奖券,一定有一次中奖,错误; C、想了解台州市城镇居民人均年收入水平,宜采用抽样调查,正确; D、我市未来三天内肯定下雪,错误 故选:C 6 (3 分)将抛物线 y3x2向左平移 2 个单位,再向下平移 1 个单位,所得抛物线为( ) Ay3(x2)21 By3(x2)2+1 Cy3(x+2)21 Dy3(x+2)2+1 【解答
12、】 解: 抛物线 y3x2向左平移 2 个单位, 再向下平移 1 个单位后的抛物线顶点坐标为 (2, 1) , 所得抛物线为 y3(x+2)21 故选:C 7 (3 分)如图,如果从半径为 9cm 的圆形纸片剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠) ,那么这个圆锥的高为( ) A6cm Bcm C8cm Dcm 【解答】解:从半径为 9cm 的圆形纸片剪去圆周的一个扇形, 剩下的扇形的角度360240, 留下的扇形的弧长12, 圆锥的底面半径 r6cm, 圆锥的高3cm 故选:B 8 (3 分)同时掷两个质地均匀的正方体骰子,骰子的六个面上分别刻有 1 到 6 的点数,则两


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2021 2022 学年 内蒙古 乌兰察布 部分 九年级 上期 数学试卷 答案 详解
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-207479.html