1、高三数学试卷 第 1 页 共 4 页 浦东新区 2021 学年度第一学期期末教学质量检测 高三数学试卷 考生注意：1、本试卷共 21 道试题，满分 150 分，答题时间 120 分钟； 2、请在答题纸上规定的地方解答，否则一律不予评分 . 一、填空题 （本大题满分一、填空题 （本大题满分 54 分） 本大题共有分） 本大题共有 12 题，题，1-6 题每题题每题 4 分，分，7-12 题每题题每题 5 分考分考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分或分或5分，否则一律得分，否则一律得零分零分 1已知复数1 2zi （
2、i为虚数单位） ，则|z . 2函数( )1f xx的反函数为1( )fx，则1(3)f . 3已知3cos5 ，则cos2的值为 . 4已知集合 | 11Axx ， |02xBxx，则ABI= . 5底面半径长为 2，母线长为 3 的圆柱的体积为 . 6三阶行列式125143356中，元素 2 的代数余子式的值为 . 7数列na的通项公式为21 (110)12(11)nnnann，则limnna . 8方程22log (1)log (1)1xx的解为 . 9. 已知函数2( )23f xxxm ，若( )0f x 对任意的1,2x恒成立，则实数m的取值范围是 . 10某学校要从 6 名男生和
3、 4 名女生中选出 3 人担任进博会志愿者，则所选 3 人中男女生都有的概率为 .（用数字作答） 11 已 知(1, 0 )A 、(1,0)B、(1, 3)P， 点C是 圆221xy上 的 动 点 ， 则PC PBPC PAuuu r uuu ruuu r uu u r的取值范围是 . 12已知实数xy、满足| 14x xy y，则|24|xy的取值范围是 . 高三数学试卷 第 2 页 共 4 页 PCBAD 二、选择题（本大题满分二、选择题（本大题满分 20 分）本大题共有分）本大题共有 4 题，每题有且题，每题有且只只有一个正确有一个正确答案答案考生考生必必须须在答题纸的相应编号上，在答题
4、纸的相应编号上，将将代表答案的小方格涂黑，选对得代表答案的小方格涂黑，选对得 5 分，否则一律得零分分，否则一律得零分 13已知直线a在平面上，则“直线l a”是“直线l ”的 （ ） （A）充分非必要条件 （B）必要非充分条件 （C）充要条件 （D）既非充分又非必要条件 1410(1)x的二项展开式中第 4 项是 （ ） （A）3710C x （B）4610C x （C）3710C x （D）4610C x 15若方程2244xkyk表示双曲线，则此双曲线的虚轴长等于 （ ） （A）2 k （B）2k （C）k （D）k 16函数1( )sin2f xx， ,40 xt t零点的个数不可能是
5、 （ ） （A）12 个 （B）13 个 （C）14 个 （D）15 个 三、解答题（本大题满分三、解答题（本大题满分 76 分）本大题共有分）本大题共有 5 题，解答下列各题必须在答题纸相应编号题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤的规定区域内写出必要的步骤 17 （本题满分 （本题满分 14 分分）本题共有本题共有 2 个小题，第个小题，第 1 小题满分小题满分 6 分，第分，第 2 小题满分小题满分 8 分分. 已知三棱锥PABC中，PA、BA、CA两两互相垂直，且长度均为 1 （1）求三棱锥PABC的全面积； （2）若点D为BC的中点，求PD与平面PAC所成角的
6、大小 （结果用反三角函数值表示） 18 （本题满分 （本题满分 14 分分）本题共有本题共有 2 个小题，第个小题，第 1 小题满分小题满分 6 分，第分，第 2 小题满分小题满分 8 分分. 已知函数2( )1f xxax，aR （1）判断函数( )f x的奇偶性，并说明理由； （2）若函数( )( )(0)f xg xxx，写出函数( )g x的单调递增区间并用定义证明 高三数学试卷 第 3 页 共 4 页 OBAPxyBOFA 19 （本题满分 （本题满分 14 分分）本题共有本题共有 2 个小题，第个小题，第 1 小题满分小题满分 6 分，第分，第 2 小题满分小题满分 8 分分. 某
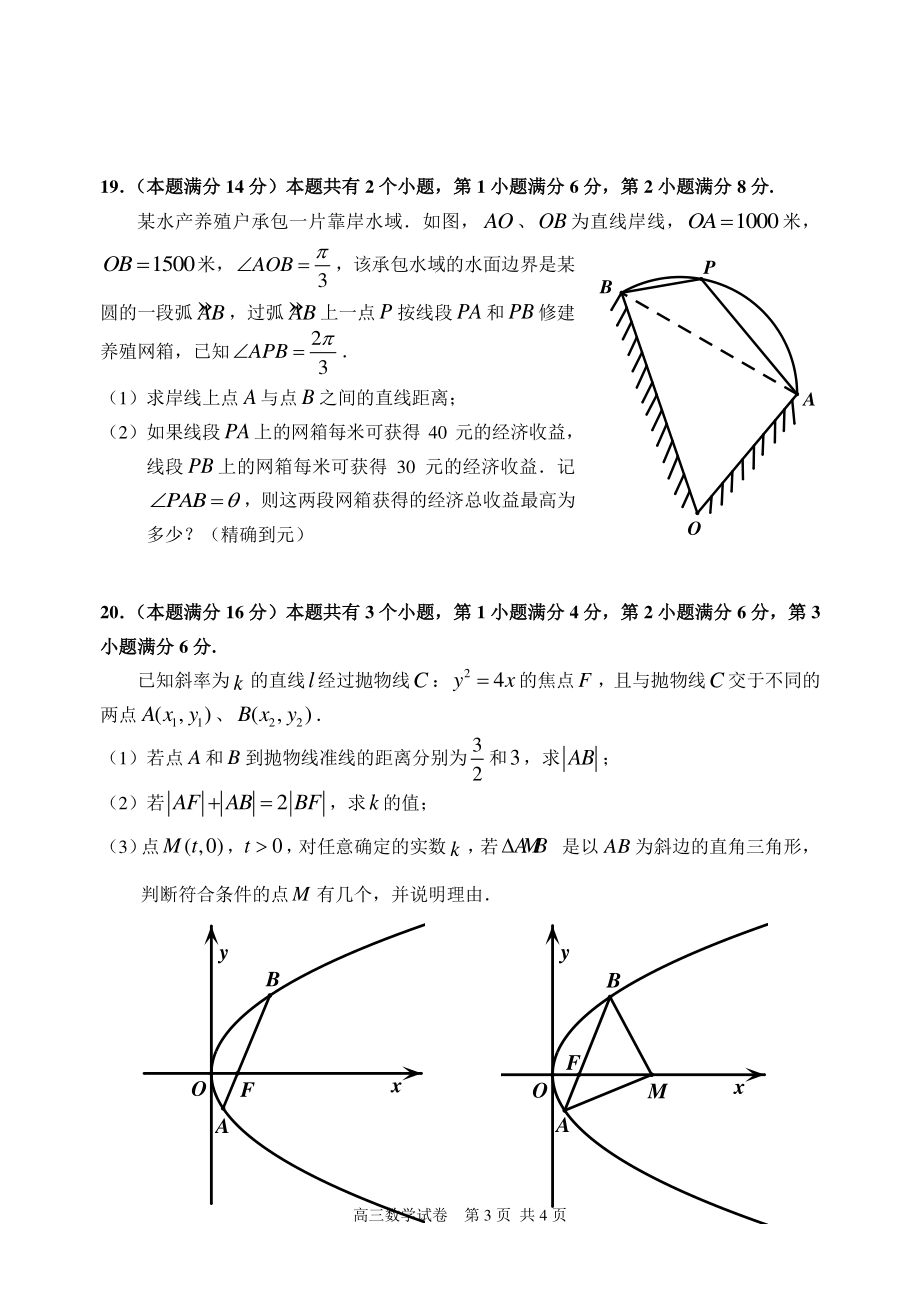
7、水产养殖户承包一片靠岸水域如图，AO、OB为直线岸线，1000OA米，1500OB米，3AOB，该承包水域的水面边界是某 圆的一段弧AB，过弧AB上一点P按线段PA和PB修建 养殖网箱，已知23APB （1）求岸线上点A与点B之间的直线距离； （2）如果线段PA上的网箱每米可获得 40 元的经济收益，线段PB上的网箱每米可获得 30 元的经济收益记PAB，则这两段网箱获得的经济总收益最高为多少？（精确到元） 20 （本题满分 （本题满分 16 分分）本题共有本题共有 3 个小题，第个小题，第 1 小题满分小题满分 4 分，第分，第 2 小题满分小题满分 6 分，第分，第 3小题满分小题满分 6
8、 分分. 已知斜率为k的直线l经过抛物线C：24yx的焦点F，且与抛物线C交于不同的两点11( ,)A x y、22(,)B xy （1）若点A和B到抛物线准线的距离分别为32和3，求AB； （2）若2AFABBF，求k的值； （3） 点( ,0)M t，0t ， 对任意确定的实数k， 若A M B是以AB为斜边的直角三角形，判断符合条件的点M有几个，并说明理由 xyBOFAM高三数学试卷 第 4 页 共 4 页 21 （本题满分 （本题满分 18 分分）本题共有本题共有 3 个小题，第个小题，第 1 小题满分小题满分 4 分，第分，第 2 小题满分小题满分 6 分，第分，第 3小题满分小题满
9、分 8 分分. 已知数列 na， 若存在A R使得数列naA-是递减数列， 则称数列 na是 “A型数列” （1）判断数列1,3 ,1,2p -是否为“0 型数列” ； （2）若等比数列 na的通项公式为nnaq=（*n N） ，0q，其前n项和为nS，且nS是“A型数列” ，求A的值和q的取值范围； （3）已知0k ，数列 na满足10a =，11nnak a+=-（*n N） 若存在A R，使得 na是“A型数列” ，求k的取值范围，并求出所有满足条件的A（用k表示） 高三数学高三数学答案答案 1 5 2 4 3 725 4 |01xx 5 12 6 3 72 8 3 9. 6,) 10
10、45 11 4,12 12 42 2,4) 13 B 14 C 15B 16 D 17解：解： （1）三棱锥PABC的全面积 133332242S .6 分 （2）取AC的中点，连接HD和HP， 因为PA 平面ABC，DH在平面ABC上， 所以PADH，又因为DHAC PCBAD高三数学试卷 第 5 页 共 4 页 所以DH 平面PAC， 所以DPH是PD与平面PAC所成角；.10 分 因为12DH ，52PH ， 所以5tan5DPH， 5arctan5DPH， 所以PD与平面PAC所成角的大小为5arctan514 分 18解： （1）当0a 时，2( )1f xx， 定义域为R， 任选x
11、R，都有2()1( )fxxf x ， 所以0a 时函数( )f x为偶函数；.3 分 当0a ，( 1)2,(1)2fa fa 则( 1)(1),( 1)(1)ffff ； 0a 时函数( )f x既非奇函数又非偶函数；.6 分 （2）函数( )g x的单调递增区间为1, 证明：( )1( )f xg xxaxx， 任取12,1,x x 且12xx .8 分 12121212121212121111()()()()(1)()()x xg xg xxaxaxxxxxxx xx x 10 分 由于12xx，则120 xx；由于12,1,x x ，则121210 x xx x； 高三数学试卷 第
12、6 页 共 4 页 所以1212121()()0 x xxxx x，即12( )()f xf x 12 分 函数( )g x的单调递增区间为1, .14 分 19 解：解： （1）222cos3ABOAOBOA OB 22150010002 1500 1000cos60500 7 ， 岸线上点A与点B之间的直线距离为500 7米.6 分 （2）PAB中，500 72sinsinsin()33PAPB， 1000 7sin()33PA，1000 7sin3PB， （03）8 分 设两段网箱获得的经济总收益为y元，则 40000 730000 74030sin()sin333yPAPB 10000
13、 710000 74sin()3sin (2 3cossin )333 10000 91sin(arctan2 3)3.12 分 当arctan2 32，即arctan2 3(0,)23时，.13 分 max10000 91550763y（元） 所以两段网箱获得的经济总收益最高约为 55076 元.14 分 20 解： （1）根据抛物线定义，3,32AFBF，92AB . 4 分. 高三数学试卷 第 7 页 共 4 页 （2）直线l的方程为1yk x， 21 ,14 .2yk xyx 2222240,3k xkxk， 0， 5 分 1221242,41.5xxkxx 6 分 12121,1,2
14、AFxBFxABxx， 2AFABBF， 11221221xxxx， 2121,6xx 8 分 221222458,33kkxxkk， 9 分 代入（5）得：2242224 58=178033kkkkkk ， 21k舍或28k ， 2 2k . 10 分 （3） AMB是以AB为斜边的直角三角形， MAMB，0MA MBuuu r uuu r， 11 分 1122,0 xtyxty, 12120 xtxty y, 即21 212120 x xt xxty y， 2121211y ykxx21 21214kx xxx， （或者221212124416,4y yxxy y ） ， 2241240t
15、tk，224230ttk， 14 分 2242120k ， 120t t ，方程仅有一个正实数解， 存在一个满足条件的点M. 16 分. 21解：解： （1）1312p ，因此是的4 分 （2）若1q=，nSAnA-=-，不存在A R使得数列nA-是递减数列， nS不是“A型数列” ； 若1q，(1)(1)11nnnqqq qSqq，因为nS为递增数列，对于任意A，存在N， 高三数学试卷 第 8 页 共 4 页 当nN时，nnSASA-=-，递增，不存在A， nS不是“A型数列” ； 若01q+-，从而12A -且1k ，矛盾.12 分 （ii）当01k，则4n. 假设nm=为使得0na 的最
16、小正整数，则10mmaa-?，故11110mmmakaak-= -?-，而12221110mmmkakaakk-= -，与m的最小性矛盾. 故0na （*n N） ，从而11nnaka+= -对一切*n N成立. 据此，可解得()111nnkak-=+. 故当11ka = -+时，11nnkaka-=+，即：naa-为递减数列. 于是 na为a型数列.16 分 再证明a是唯一解. 用反证法. 假设存在Aa使得 na是A型数列. 若Aa，则由22211mmkaka-=+得，当()()2log11kmAka轾-+犏臌时，21maA-. 故222212111mmmmkkaAAAaAkkaa-+-=-=-+，naA-不是递减数列， 从而 na不是A型数列. 同理可证Aa时 na也不是A型数列.18 分 综上，()0,1k ，相应的11Ak= -+.
