1、2019-2020 学年安徽省合肥市庐阳区九年级学年安徽省合肥市庐阳区九年级上期末数学试卷上期末数学试卷 一、选择题（本大题共 10 小题，每小题 4 分，满分 40 分） 1抛物线 y3（x2）2+5 的顶点坐标是（ ） A （2，5） B （2，5） C （2，5） D （2，5） 2下列图形中，是中心对称图形但不是轴对称图形的是（ ） A B C D 3若，则的值（ ） A B C D 4要将抛物线 yx2平移后得到抛物线 yx2+2x+3，下列平移方法正确的是（ ） A向左平移 1 个单位，再向上平移 2 个单位 B向左平移 1 个单位，再向下平移 2 个单位 C向右平移 1 个单位，
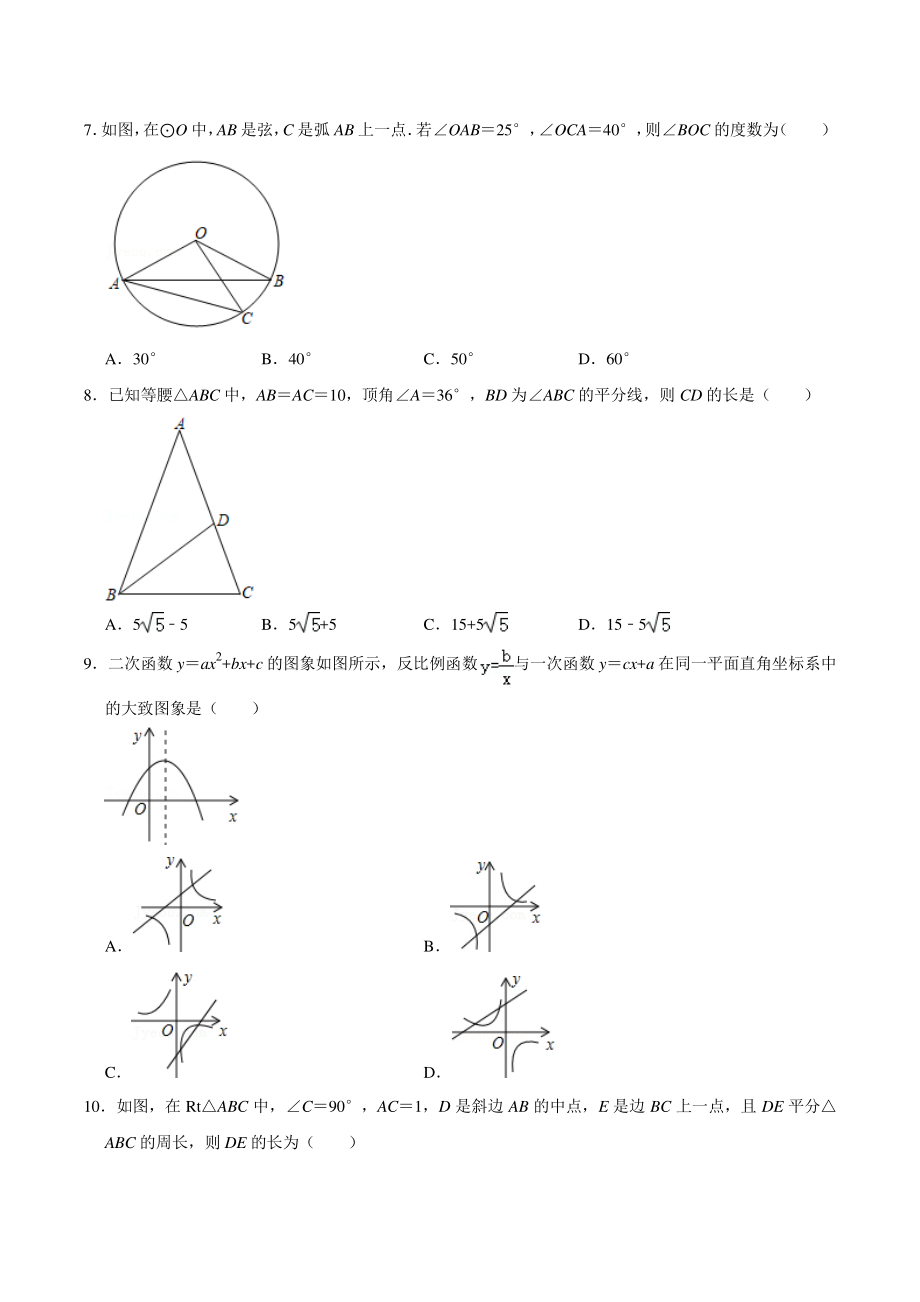
2、再向上平移 2 个单位 D向右平移 1 个单位，再向下平移 2 个单位 5如图，D、E 在ABC 的边上，如果 DEBC，AE：BE1：2，BC6，那么 DE 的长为（ ） A B2 C D3 6如图，已知一商场自动扶梯的长 l 为 13 米，高度 h 为 5 米，自动扶梯与地面所成的夹角为 ，则 tan的值等于（ ） A B C D 7 如图， 在O 中， AB 是弦， C 是弧 AB 上一点 若OAB25， OCA40， 则BOC 的度数为 （ ） A30 B40 C50 D60 8已知等腰ABC 中，ABAC10，顶角A36，BD 为ABC 的平分线，则 CD 的长是（ ） A55 B5
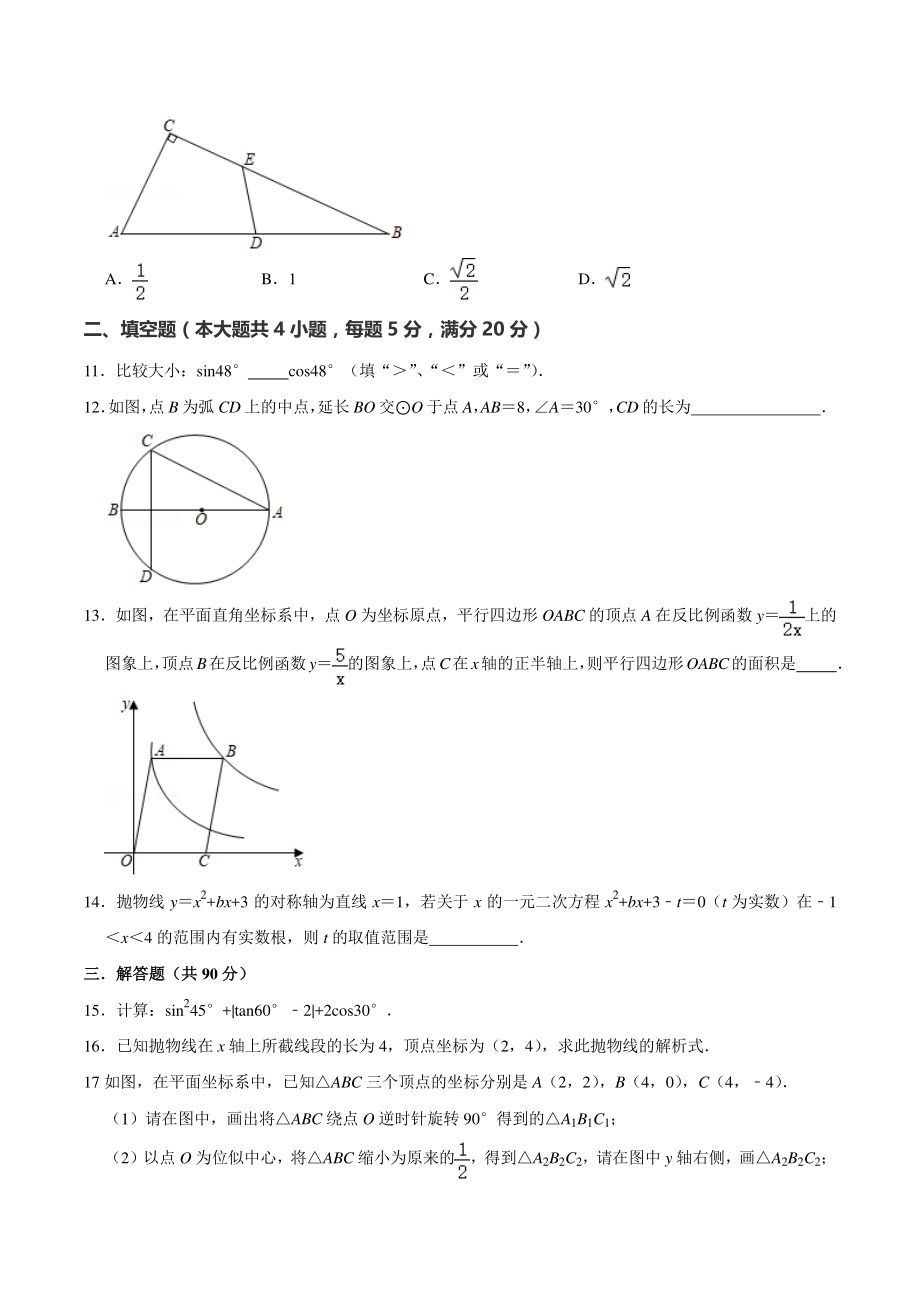
3、+5 C15+5 D155 9二次函数 yax2+bx+c 的图象如图所示，反比例函数与一次函数 ycx+a 在同一平面直角坐标系中的大致图象是（ ） A B C D 10如图，在 RtABC 中，C90，AC1，D 是斜边 AB 的中点，E 是边 BC 上一点，且 DE 平分ABC 的周长，则 DE 的长为（ ） A B1 C D 二、填空题（本大题共 4 小题，每题 5 分，满分 20 分） 11比较大小：sin48 cos48（填“” 、 “”或“” ） 12 如图， 点 B 为弧 CD 上的中点， 延长 BO 交O 于点 A， AB8， A30， CD 的长为 13如图，在平面直角坐标
4、系中，点 O 为坐标原点，平行四边形 OABC 的顶点 A 在反比例函数 y上的图象上， 顶点B在反比例函数y的图象上， 点C在x轴的正半轴上， 则平行四边形OABC的面积是 14抛物线 yx2+bx+3 的对称轴为直线 x1，若关于 x 的一元二次方程 x2+bx+3t0（t 为实数）在1x4 的范围内有实数根，则 t 的取值范围是 三解答题（共三解答题（共 90 分分） 15计算：sin245+|tan602|+2cos30 16已知抛物线在 x 轴上所截线段的长为 4，顶点坐标为（2，4） ，求此抛物线的解析式 17 如图，在平面坐标系中，已知ABC 三个顶点的坐标分别是 A（2，2）
5、，B（4，0） ，C（4，4） （1）请在图中，画出将ABC 绕点 O 逆时针旋转 90得到的A1B1C1； （2）以点 O 为位似中心，将ABC 缩小为原来的，得到A2B2C2，请在图中 y 轴右侧，画A2B2C2； （3）tanBAC 18 如图所示，巡逻船在 A 处测得灯塔 C 在北偏东 45方向上，距离 A 处 30km在灯塔 C 的正南方向 B 处有一渔船发出求救信号，巡逻船接到指示后立即前往施救已知 B 处在 A 处的北偏东 60方向上，这时巡逻船与渔船的距离是多少？ （精确到 0.01km参考数据：1.414，1.732，2.449） 19 如图，在 RtABC 中，BAC90，
6、ABAC2，D 是边 BC 上异于 B、C 的一个动点，过点 D 作ADE45，DE 交 AC 于点 E （1）求ABDDCE； （2）设 BDx，AEy，求 y 与 x 之间的函数关系式，并求 x 的取值范围 20 如图，点 A（1，6） ，B（3，m）是直线 AB 与反比例函数 y（x0）的图象的两个交点，ACx 轴，垂足为 C，已知 D（0，1） ，连接 AD，BD，BC （1）求直线 AB 的表达式； （2）ABC 和ABD 的面积分别为 S1，S2，求 S2S1 21 如图，在ABC 中，BC 是O 的直径，D 是弧 CE 的中点 （1）求证：ABBC； （2）若 AD3，AE2，求
7、 BC 的长 22 任意球是足球比赛的主要得分手段之一在某次足球赛中，甲球员站在点 O 处发出任意球，如图，把球看作点，其运行的高度 y（m）与运行的水平距离 x（m）满足关系式 ya（x12）2+h，已知防守队员组成的人墙与O点的水平距离为9m， 防守队员跃起后的高度为2.1m， 对方球门与O点的水平距离为18m，球门高是 2.43m （假定甲球员的任意球恰好能射正对方的球门） （1）当 h3 时，求 y 与 x 的关系式（不要求写出自变量 x 的取值范围） ； （2）当 h3 时，足球能否越过人墙？足球会不会踢飞（球从球门的上方飞过）？请说明理由 （3）若甲球员发出的任意球直接射进对方球门
8、得分，求 h 的取值范围 23 在ABC 中，CACB，ACB点 P 是平面内不与点 A，C 重合的任意一点连接 AP，将线段 AP绕点 P 逆时针旋转 得到线段 DP，连接 AD，BD，CP （1）观察猜想 如图 1，当 60时，的值是 ，直线 BD 与直线 CP 相交所成的较小角的度数是 （2）类比探究 如图 2，当 90时，请写出的值及直线 BD 与直线 CP 相交所成的较小角的度数，并就图 2 的情形说明理由 （3）解决问题 当 90时，若点 E，F 分别是 CA，CB 的中点，点 P 在直线 EF 上，请直接写出点 C，P，D 在同一直线上时的值 参考答案参考答案 一选择题（共一选择
9、题（共 10 小题）小题） 1 C 2 A 3 C 4 A 5 B 6 A 7 A 8 D 9 C 二填空题（共二填空题（共 4 小题）小题） 11 12 4 13 2 14 2t11 三解答题三解答题 15解：原式（）2+2+2 +2+ 16解：抛物线顶点坐标为（2，4） ，且在 x 轴上截得线段长为 4， 对称轴为直线 x2，与 x 轴两交点坐标为（0，0） ， （4，0） ， 设抛物线解析式为 ya（x2）2+4， 把 x0，y0 代入得：4a+40， 解得 a1 则抛物线解析式为 y（x2）2+4x2+4x 17 解： （1）如图，A1B1C1为所作； （2）如图，A2B2C2为所作；
10、 （3）作 BHAC 于 H，如图， BH，AB2， tanBAH， 即 tanBAC 故答案为 18 解：延长 CB 交过 A 点的正东方向于 D，如图所示： 则CDA90， 由题意得：AC30km，CAD904545，BAD906030， ADCDAC15，ADBD， BD5， AB10102.44924.49（km） ； 答：巡逻船与渔船的距离约为 24.49km 19 （1）证明：由图知和已知条件： ADBDAC+CDAC+45， DECDAC+ADEDAC+45， ADBDEC； BC， ABDDCE （2）解：BAC90，ABAC2， BC2， 由ABDDCE， ， AB2，BDx
11、，DC2x，CE2y， 代入得， 42y2xx2， yx2x+2 （0 x） 20 解： （1）由点 A（1，6） ，B（3，m）在反比例函数 y（x0）的图象上， n166， 反比例函数的解析式为 y（x0） ， 将点 B（3，m）代入 y（x0）得 m2， B（3，2） ， 设直线 AB 的表达式为 ykx+b， ，解得， 直线 AB 的表达式为 y2x+8； （2）由点 A，B 坐标得 AC6，点 B 到 AC 的距离为 312， S1613， 设 AB 与 y 轴的交点为 E，可得 E（0，6） ，如图： 由直线 y2x+8 可知，E（0，8） ， D（0，1） ， DE817， S2
12、SBDESAED7317， S2S1734 21 （1）证明：连接 BD， BC 是O 的直径， BDC90， ADBBDC90， A+ABD90，C+CBD90， D 是弧 CE 的中点， ， ABDCBD， AC， ABBC； （2）解：ABBC，BDAC，AD3， CDAD3， 连接 DE， 四边形 BCDE 是O 的内接四边形， ADEB， AA， ADEABC， ， AE2，ADCD3， ， AB9， ABBC， BC9 22 解： （1）当 h3 时，ya（x12）2+3， 抛物线 ya（x12）2+3 经过点（0，0） ， 0a（012）2+3， 解得：a， y 与 x 的关系式
13、 y（x12）2+3； （2）当 h3 时，足球能越过人墙，足球会不会踢飞，理由如下： 当 h3 时，由（1）得 y（x12）2+3， 当 x9 时，y+32.812.1， 足球能过人墙， 当 x18 时，y2.252.43， 足球能直接射进球门； （3）由题设知 ya（x12）2+h，函数图象过点（0，0） ， 得 0a（012）2+h，即 144a+h0， 由足球能越过人墙，得 9a+h2.1， 由足球能直接射进球门，得 036a+h2.43， 由得 a， 把代入得 9（）+h2.1， 解得 h2.24， 把代入得 036（）+h2.43， 解得 0h3.24， h 的取值范围是 2.24
14、h3.24 23 解： （1）如图 1 中，延长 CP 交 BD 的延长线于 E，设 AB 交 EC 于点 O PADCAB60， CAPBAD， CABA，PADA， CAPBAD（SAS） ， PCBD，ACPABD， AOCBOE， BEOCAO60， 1，直线 BD 与直线 CP 相交所成的较小角的度数是 60， 故答案为 1，60 （2）如图 2 中，设 BD 交 AC 于点 O，BD 交 PC 于点 E PADCAB45， PACDAB， ， DABPAC， PCADBA， EOCAOB， CEOOAB45， 直线 BD 与直线 CP 相交所成的较小角的度数为 45 （3）如图 3
15、1 中，当点 D 在线段 PC 上时，延长 AD 交 BC 的延长线于 H CEEA，CFFB， EFAB， EFCABC45， PAO45， PAOOFH， POAFOH， HAPO， APC90，EAEC， PEEAEC， EPAEAPBAH， HBAH， BHBA， ADPBDC45， ADB90， BDAH， DBADBC22.5， ADBACB90， A，D，C，B 四点共圆， DACDBC22.5，DCAABD22.5， DACDCA22.5， DADC，设 ADa，则 DCADa，PDa， 2 解法二：在 RtPAD 中，E 是 AC 的中点， PEEAEC， EPCECP， CEF45EPC+ECP， EPCECP22.5， PDA45ACD+DAC， DAC22.5， ADDC， 设 PDa，则 ADDCa， 2 如图 32 中，当点 P 在线段 CD 上时，同法可证：DADC，设 ADa，则 CDADa，PDa， PCaa， 2+
