1、首 页 末 页 第一部分第一部分 数与代数数与代数 第三章第三章 方程与方程组方程与方程组 考考 点点 管管 理理 中中 考考 再再 现现 课课 时时 作作 业业 归归 类类 探探 究究 第第9 9课时课时 一元二次方程一元二次方程 首 页 末 页 考考 点点 管管 理理 1一元二次方程的概念一元二次方程的概念 定义：定义：只含有只含有 个未知数，并且未知数的最高次数是个未知数，并且未知数的最高次数是 的整式方程，叫做的整式方程，叫做一元二次方程，其一般形式为一元二次方程，其一般形式为 2一元二次方程的解法一元二次方程的解法 直接开平方法：直接开平方法：它适合于形式为它适合于形式为(xa)2b
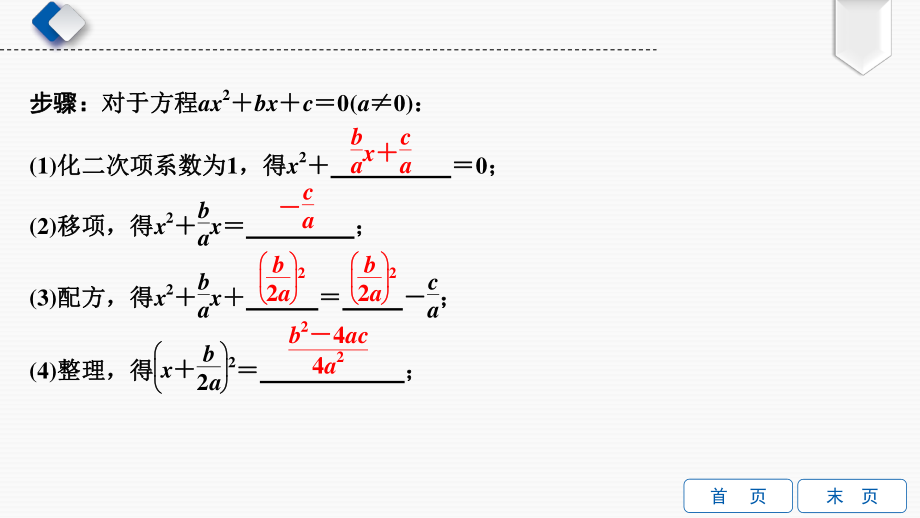
2、(b0)或或(axb)2(cxd)2的方程的方程 配方法：配方法：通过配成完全平方形式解一元二次方程的方法，叫做配方法通过配成完全平方形式解一元二次方程的方法，叫做配方法 2 ax2bxc0(a0) 1 首 页 末 页 步骤：步骤：对于方程对于方程ax2bxc0(a0)： (1)化二次项系数为化二次项系数为1，得，得x2 0； (2)移项，得移项，得x2bax ； (3)配方，得配方，得x2bax ca； (4)整理整理，得得 xb2a2 ； baxca ca b2a2 b2a2 b24ac4a2 首 页 末 页 (5)直接开平方，得直接开平方，得xb2a ； (6)移项，得移项，得x . 注
3、意：注意：配方的关键是在方程两边都加上一次项系数的一半的平方配方的关键是在方程两边都加上一次项系数的一半的平方 公式法：公式法：当当b24ac0时，方程时，方程ax2bxc0(a0)的求根公式是的求根公式是 _. b24ac2a b b24ac2a xb b24ac2a 首 页 末 页 步骤：步骤：(1)将方程化成将方程化成ax2bxc0(a0)的形式；的形式； (2)确定确定a，b，c的值；的值； (3)求出求出b24ac的值；的值； (4)若若b24ac0，则可用求根公式求解；若，则可用求根公式求解；若b24ac0方程方程 的实数根；的实数根； (2)b24ac0方程方程 的实数根；的实数
4、根； (3)b24ac0， 方程方程2x23x50有两个不相等的实数根故选有两个不相等的实数根故选B. 首 页 末 页 32019 衡阳衡阳国家实施国家实施“精准扶贫精准扶贫”政策以来，很多贫困人口走向了致富的道政策以来，很多贫困人口走向了致富的道路，某地区截至路，某地区截至2016年年底，有贫困人口年年底，有贫困人口9万人，通过社会各界的努力，截至万人，通过社会各界的努力，截至2018年年底，该地区的贫困人口减少至年年底，该地区的贫困人口减少至1万人设万人设2016年年底至年年底至2018年年底该地年年底该地区贫困人口的年平均下降率为区贫困人口的年平均下降率为x，根据题意列方程得，根据题意列
5、方程得( ) A9(12x)1 B.9(1x)21 C9(12x)1 D.9(1x)21 B 首 页 末 页 42019 娄底娄底已知方程已知方程x2bx30的一根为的一根为 5 2，则方程的另一根为，则方程的另一根为 _. 5 2 【解析】【解析】 设原方程的另一个根为设原方程的另一个根为x1，则由一元二次方程的根与系数的关系，则由一元二次方程的根与系数的关系x1x2ca，得，得x1 5 23， x135 23 5 2 5 2 5 2 5 2. 首 页 末 页 52019 邵阳邵阳关于关于x的一元二次方程的一元二次方程x22xm0有两个不相等的实数根，则有两个不相等的实数根，则m的最小整数值
6、是的最小整数值是 . 0 【解析】【解析】 一元二次方程一元二次方程x22xm0有两个不相等的实数根，有两个不相等的实数根， 44m0，m1. 故故m的最小整数值为的最小整数值为0. 首 页 末 页 62019 常德常德解方程：解方程：x23x20. 解：解：x23x20. a1，b3，c2， b24ac17， x13 172，x23 172. 首 页 末 页 归归 类类 探探 究究 类型之一类型之一 一元二次方程及其解的概念一元二次方程及其解的概念 2019 遂宁遂宁已知关于已知关于x的一元二次方程的一元二次方程(a1)x22xa210有一个根为有一个根为x0，则，则a的值为的值为 ( )
7、A0 B. 1 C1 D.1 D 首 页 末 页 【解析】【解析】 当当x0时，时，a210，a 1. 原方程是一元二次方程，原方程是一元二次方程，a1，a1.故选故选D. 【点悟】【点悟】 (1)含一个未知数，并且未知数的最高次数为含一个未知数，并且未知数的最高次数为2的整式方程叫做一元二的整式方程叫做一元二次方程，其一般式为次方程，其一般式为ax2bxc0(a0) (2)本题考查的是方程根的含义，若已知方程的根，求方程中的其他字母的值，可本题考查的是方程根的含义，若已知方程的根，求方程中的其他字母的值，可以直接将这个根代入方程以直接将这个根代入方程 首 页 末 页 12018 长沙长沙已知
8、关于已知关于x的方程的方程x23xa0有一个根为有一个根为1，则方程的另一个根为，则方程的另一个根为 . 2 【解析】【解析】 方法一：把方法一：把x1代入方程代入方程x23xa0，得，得13a0.解得解得a2. 把把a2代入原方程，得代入原方程，得x23x20. 解得解得x11，x22. 方程的另一个根为方程的另一个根为2. 首 页 末 页 方法二：设方程的两根为方法二：设方程的两根为x1，x2， 由一元二次方程的根与系数的关系可知，由一元二次方程的根与系数的关系可知， x1x2313， x11，x22. 首 页 末 页 类型之二类型之二 一元二次方程的解法一元二次方程的解法 解方程：解方程
9、：3x22x20.(用配方法和公式法两种方法用配方法和公式法两种方法) 解：解：(解法一解法一)移项，得移项，得3x22x2. 配方，得配方，得3 x13273. 解得解得x11 73，x21 73. 首 页 末 页 (解法二解法二)a3，b2，c2， (2)243(2)42428. x2 2 723.x11 73，x21 73. 首 页 末 页 22019 齐齐哈尔齐齐哈尔解方程：解方程：x26x7. 解：解：配方，得配方，得x26x979， 因此因此(x3)22， 由此得由此得x3 2， 解得解得x13 2，x23 2. 【点悟】【点悟】 解一元二次方程的方法有直接开方法、因式分解法、配方
10、法、公式法解一元二次方程的方法有直接开方法、因式分解法、配方法、公式法等一般地，在不能直接用因式分解法时，可选择配方法或公式法来解等一般地，在不能直接用因式分解法时，可选择配方法或公式法来解 首 页 末 页 类型之三类型之三 一元二次方程根的判别式一元二次方程根的判别式 2019 聊城聊城若关于若关于x的一元二次方程的一元二次方程(k2)x22kxk6有实数根，则有实数根，则k的的取值范围为取值范围为( ) Ak0 B.k0且且k2 Ck32 D.k32且且k2 D 首 页 末 页 【解析】【解析】 原方程是一元二次方程，原方程是一元二次方程， k20，k2. 其有实数根，其有实数根，(2k)
11、24(k2)(k6)0， 解得解得k32，k的取值范围为的取值范围为k32且且k2.故选故选D. 首 页 末 页 32019 陇南陇南关于关于x的一元二次方程的一元二次方程x2m x10有两个相等的实数根，则有两个相等的实数根，则m的取值为的取值为 . 4 【解析】【解析】 关于关于x的一元二次方程的一元二次方程x2 mx10有两个相等的实数根，有两个相等的实数根， ( m)24110，解得，解得m4. 首 页 末 页 42019 泰安泰安已知关于已知关于x的一元二次方程的一元二次方程x2(2k1)xk230有两个不相等的有两个不相等的 实数根，则实数实数根，则实数k的取值范围是的取值范围是
12、. k0， 解得解得k0， a3. a为正整数，为正整数， a1,2. 首 页 末 页 (2)x1x22(a1)，x1x2a2a2， 又又x21x22x1x216， 则则(x1x2)23x1x216， 2(a1)23(a2a2)16， 解得解得a11，a26. a0， 解得解得k34. (2)由根与系数的关系可知由根与系数的关系可知x1x2ba2k1， 2k13，解得，解得k134(符合题意符合题意) 把把k1代入原方程，得代入原方程，得x23x20， 解得解得x11，x22. 首 页 末 页 【点悟】【点悟】 (1)用一元二次方程的根与系数的关系求字母的值时，要代入用一元二次方程的根与系数的
13、关系求字母的值时，要代入b24ac检验是否满足检验是否满足b24ac0； (2)一元二次方程的根与系数的关系常用于求有关的代数式的值，体现了整体思一元二次方程的根与系数的关系常用于求有关的代数式的值，体现了整体思想想 首 页 末 页 类型之五类型之五 一元二次方程的应用一元二次方程的应用 2019 长沙长沙近日，长沙市教育局出台长沙市中小学教师志愿辅导工作实近日，长沙市教育局出台长沙市中小学教师志愿辅导工作实施意见鼓励教师参与施意见鼓励教师参与志愿辅导，某区率先示范，推出名师公益大课堂，为学生志愿辅导，某区率先示范，推出名师公益大课堂，为学生提供线上线下免费辅导，据统计，第一批公益课受益学生达
14、提供线上线下免费辅导，据统计，第一批公益课受益学生达2万人次，第三批公万人次，第三批公益课受益学生达益课受益学生达2.42万人次万人次 (1)如果第二批、第三批公益课受益学生人次的增长率相同，求这个增长率；如果第二批、第三批公益课受益学生人次的增长率相同，求这个增长率； (2)按照这个增长率，预计第四批公益课受益学生将达到多少万人次？按照这个增长率，预计第四批公益课受益学生将达到多少万人次？ 首 页 末 页 解：解：(1)设增长率为设增长率为x，根据题意，得，根据题意，得 2(1x)22.42， 解得解得x12.1(舍去舍去)，x20.110%. 答：增长率为答：增长率为10%. (2)2.4
15、2(110%)2.662(万人次万人次) 答：第四批公益课受益学生将答：第四批公益课受益学生将达到达到2.662万人次万人次 首 页 末 页 课课 时时 作作 业业 (70分分) 一、选择题一、选择题(每题每题4分，共分，共24分分) 12019 滨州滨州用配方法解一元二次方程用配方法解一元二次方程x24x10时，下列变形正确的是时，下列变形正确的是( ) A(x2)21 B.(x2)25 C(x2)23 D.(x2)23 D 首 页 末 页 【解析】【解析】 x24x10，移项，得，移项，得x24x1，两边配方，得，两边配方，得x24x414，即，即(x2)23.故选故选D. 首 页 末 页
16、 22019 盐城盐城关于关于x的一元二次方程的一元二次方程x2kx20(k为实数为实数)根的情况是根的情况是( ) A有两个不相等的实数根有两个不相等的实数根 B有两个相等的实数根有两个相等的实数根 C没有实数根没有实数根 D不能确定不能确定 A 首 页 末 页 【解析】【解析】 a1，bk，c2， b24ack241(2)k280， 方程有两个不相等的实数根故选方程有两个不相等的实数根故选A. 首 页 末 页 32019 兰州兰州x1是关于是关于x的一元二次方程的一元二次方程x2ax2b0的解，则的解，则2a4b( ) A2 B.3 C4 D.6 【解析】【解析】 将将x1代入代入原方程得
17、原方程得1a2b0，a2b1.2a4b2.故选故选A. A 首 页 末 页 42019 新疆新疆若关于若关于x的一元二次方程的一元二次方程(k1)x2x10有两个实数根，则有两个实数根，则k的的取值范围是取值范围是( ) Ak54 B.k54 Ck4 200. 答：答：2019年该贫困户的家庭年人均纯收入能达到年该贫困户的家庭年人均纯收入能达到4 200元元 首 页 末 页 13(10分分)2019 东营东营为加快新旧动能转换，提高公司经济效益，某公司决定对为加快新旧动能转换，提高公司经济效益，某公司决定对近期研发出的一种电子产品进行降价促销，使生产的电子产品能够及时售出，根近期研发出的一种电
18、子产品进行降价促销，使生产的电子产品能够及时售出，根据市场调查：这种电子产品销售单价定为据市场调查：这种电子产品销售单价定为200元时，每天可售出元时，每天可售出300个；若销售单个；若销售单价每降低价每降低1元，每天可多售出元，每天可多售出5个已知每个已知每个电子产品的固定成本为个电子产品的固定成本为100元，问这元，问这种电子产品降价后的销售单价为多少元时，公司每天可获利种电子产品降价后的销售单价为多少元时，公司每天可获利32 000元？元？ 首 页 末 页 解：解：设降价后的销售单价为设降价后的销售单价为x元，则降价后每天可售出元，则降价后每天可售出3005(200 x)个，个， 依题意
19、，得依题意，得(x100)3005(200 x)32 000， 整理，得整理，得x2360 x32 4000， 解得解得x1x2180. 1001800，解得，解得a13且且a0. a13且且a0 首 页 末 页 16(10分分)2019 衡阳衡阳关于关于x的一元二次方程的一元二次方程x23xk0有实数根有实数根 (1)求求k的取值范围；的取值范围； (2)如果如果k是符合条件的最大整数，且关于是符合条件的最大整数，且关于x的一元二次方程的一元二次方程(m1)x2xm30与方程与方程x23xk0有一个相同的根，求此时有一个相同的根，求此时m的值的值 首 页 末 页 解：解：(1)由一元二次方程
20、由一元二次方程x23xk0有实数根，得判别式有实数根，得判别式94k0， k94. (2)k的最大整数值为的最大整数值为2， 方程方程x23x20的根为的根为1和和2. 首 页 末 页 方程方程x23xk0与一元二次方程与一元二次方程(m1)x2xm30有一个相同根，有一个相同根， 当当x1时，有时，有(m1)1m30， 解得解得m32； 当当x2时，有时，有(m1)222m30， 解得解得m1(不合题意不合题意)， 故故m32. 首 页 末 页 (10分分) 17(10分分)2019 南充南充已知关于已知关于x的一元二次方程的一元二次方程x2(2m1)xm230有实数有实数根根 (1)求实数求实数m的取值范围；的取值范围； (2)当当m2时，方程的根为时，方程的根为x1，x2，求代数式，求代数式(x212x1)(x224x22)的值的值 首 页 末 页 解：解：(1)由题意由题意0， (2m1)24(m23)0， m134. (2)当当m2时，方程为时，方程为x23x10， x1x23，x1x21， (x212x1)(x224x22)(x213x1x1)(x223x2x22)(1x1)(1x22)(1x1)(x21)x2x1x21x1(x1x2)x1x21(3)111.
