1、2021-2022 学年辽宁省沈阳市大东区七年级（上）期中数学试卷学年辽宁省沈阳市大东区七年级（上）期中数学试卷 一、选择题（下列各题的备选答案中，只有一个答案是正确的。每小题一、选择题（下列各题的备选答案中，只有一个答案是正确的。每小题 2 分，共分，共 20 分）分） 1. 7 的相反数是（ ） A. 7 B. 17 C. 7 D. 1 2. 中国幅员辽阔，陆地面积约为 960 万平方公里，960 万用科学记数法表示为（ ） A. 0.96 107 B. 9.6 106 C. 96 105 D. 9.6 102 3. 下列各图中，经过折叠能围成一个正方体的是( ) A. B. C. D.
2、4. 实数 a，b，c，d在数轴上的对应点的位置如图所示，则正确的结论是（ ） A. a4 B. bd0 C. |a|d| D. b+c0 5. 在0.1428中用数字 3替换其中的一个非 0 数码后，使所得的数最大，则被替换的字是（ ） A. 1 B. 2 C. 4 D. 8 6. 下列说法正确的是（ ） A. 12不是整式 B. 2x2y与 y2x是同类项 C. y是单项式 D. 3x2y的次数是 4 7. 当 x2 时，代数式 ax3+bx+1的值为 6，那么当 x2 时，这个代数式的值是（ ） A. 1 B. 4 C. 6 D. 5 8. 如图，下列说法错误是( ) A. ECA是一个
3、平角 B. ADE也可以表示为D C. BCA也可以表示为1 D. ABC也可以表示为B 9. 已知AOB=30 ，BOC=45 ，则AOC 等于（ ） A. 15 B. 75 C. 15或 75 D. 不能确定 10. 下列说法正确的有（ ） n棱柱有 2n 个顶点，2n条棱， （n+2）个面（n 为不小于 3的正整数） ； 点动成线，线动成面，面动成体； 圆锥的侧面展开图是一个圆； 用平面去截一个正方体，截面的形状可以是三角形、四边形、五边形、六边形 A. 1个 B. 2个 C. 3个 D. 4个 二、填空题（每小题二、填空题（每小题 3 分，共分，共 18 分）分） 11. 在我校第 8
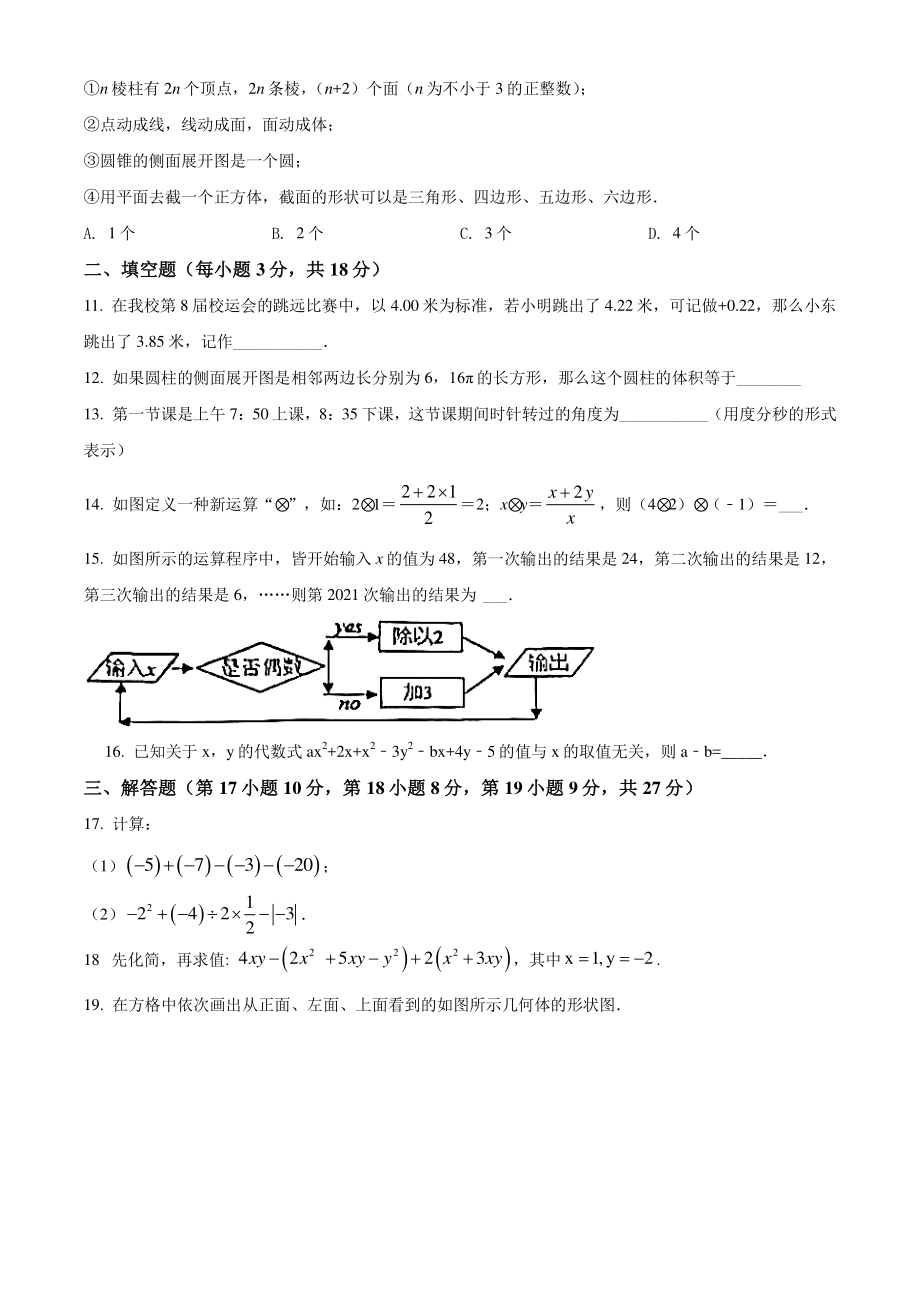
4、 届校运会的跳远比赛中，以 4.00 米为标准，若小明跳出了 4.22米，可记做+0.22，那么小东跳出了 3.85 米，记作_ 12. 如果圆柱的侧面展开图是相邻两边长分别为 6，16的长方形，那么这个圆柱的体积等于_ 13. 第一节课是上午 7：50上课，8：35下课，这节课期间时针转过的角度为_（用度分秒的形式表示） 14. 如图定义一种新运算“ ”，如：2 122 12 2；x y2xyx，则（4 2） （1）_ 15. 如图所示的运算程序中，皆开始输入 x的值为 48，第一次输出的结果是 24，第二次输出的结果是 12，第三次输出的结果是 6，则第 2021 次输出的结果为 _ 16
5、. 已知关于 x，y的代数式 ax2+2x+x23y2bx+4y5的值与 x 的取值无关，则 ab=_ 三、解答题（第三、解答题（第 17 小题小题 10 分，第分，第 18 小题小题 8 分，第分，第 19 小题小题 9 分，共分，共 27 分）分） 17. 计算： （1） 57320 ； （2）2124232 18 先化简，再求值: 22242 523xyxxyyxxy，其中x1,y2 . 19. 在方格中依次画出从正面、左面、上面看到的如图所示几何体的形状图 四、 （第四、 （第 20 小题小题 7分，第分，第 21 小题小题 12 分，共分，共 19 分）分） 20. 如图，已知四点
6、A，B，C，D，请用直尺按要求完成作图 （1）作射线 AD； （2）作直线 BC； （3）连接 BD，请在 BD上确定点 P，使 AP+CP的值最小，并说明理由 21 一辆货车从货场A出发，向东走 2千米到达批发部B，继续向东走 1.5千米到达商场C，又向西走 5.5千米到达超市D，最后回到货场 （1）以货场为原点，以东为正方向，用一个单位长度表示 1千米，你能在数轴上分别表示出货场A，批发部B，商场C，超市D的位置吗？ （2）超市D距离货场A多远？ （3）此货车每千米耗油 0.1 升，每升汽油 6.20元，请计算此货车一共需要多少汽油费？ 五五.（本题（本题 8 分）分） 22. 将 7张相
7、同的小长方形纸片（如图 1所示）按图 2所示的方式不重叠的放在长方形 ABCD 内，未被覆盖的部分恰好被分割为两个长方形，面积分别为 S1，S2，已知小长方形纸片的长为 a，宽为 b，且 ab （1）当 a9，b2，AD30时，请求： 长方形 ABCD面积； S2S1的值 （2）当 AD30 时，请用含 a，b 的式子表示 S2S1的值 六、 （本题六、 （本题 6 分）分） 23. 观察下列等式，探究其中的规律并解答问题： 112 2+3+432 3+4+5+6+752 4+5+6+7+8+9+10k2 （1）第 4 个等式中，k ； （2）写出第 s个等式： ； （3）写出第 n 个等式：
8、 （其中 n 为正整数） 七、 （本题七、 （本题 10 分）分） 24. 如图 1，直线 DE 上有一点 O，过点 O 在直线 DE 上方作射线 OC，将一直角三角板 AOB（其中OAB30）的直角顶点放在点 O 处，一条直角边 OA在射线 OD上，另一边 OB在直线 DE上方，将直角三角板绕着点 O按每秒 10的速度逆时针旋转一周，设旋转时间为 t秒 （1）当直角三角板旋转到如图 2 的位置时，OA 恰好平分COD，此时，BOC与BOE之间有何数量关系 ； （2）若射线 OC 的位值保持不变，且COE140 在旋转的过程中，是否存在某个时刻，使得射线 OA，OC，OD 中的某一条射线是另两
9、条射线所夹角的角平分线？若存在，请直接写出所有满足题意 t的取值 ，若不存在，请说明理由； 在旋转的过程中，当边 AB 与射线 OE 相交时，如图 3，请直接写出AOCBOE的值 八、 （本题八、 （本题 12 分）分） 25. 点 O为数轴的原点，点 A、B 在数轴上的位置如图所示，点 A 表示的数为 5，线段 AB的长为线段 OA长的 1.2倍.点 C在数轴上，M为线段 OC的中点 （1）点 B 表示数为_ （2）若线段 BM 的长为 4.5，则线段 AC 的长为_ （3）若线段 AC的长为 x，求线段 BM的长（用含 x 的式子表示） 2021-2022 学年辽宁省沈阳市大东区七年级（上
10、）期中数学试卷学年辽宁省沈阳市大东区七年级（上）期中数学试卷 一、选择题（下列各题的备选答案中，只有一个答案是正确的。每小题一、选择题（下列各题的备选答案中，只有一个答案是正确的。每小题 2 分，共分，共 20 分）分） 1. 7 的相反数是（ ） A 7 B. 17 C. 7 D. 1 【答案】C 【解析】 【分析】根据相反数的定义，只有符号不同的两个数，则这两数互为相反数，即可求解 【详解】解：7的相反数是 7 故选：C 【点睛】本题主要考查了相反数的定义，熟练掌握相反数的定义是解题的关键 2. 中国幅员辽阔，陆地面积约为 960 万平方公里，960 万用科学记数法表示为（ ） A. 0.
11、96 107 B. 9.6 106 C. 96 105 D. 9.6 102 【答案】B 【解析】 【详解】试题分析：960 万用科学记数法表示为 9.6 106，故选 B 考点：科学记数法表示较大的数 3. 下列各图中，经过折叠能围成一个正方体的是( ) A. B. C. D. 【答案】A 【解析】 【详解】由平面图形的折叠及正方体的展开图解题，注意只要有田、凹字格的展开图都不是正方体的表面展开图 A、可以折叠成一个正方体； B、是凹字格，故不能折叠成一个正方体； C、折叠后有两个面重合，缺少一个底面，所以也不能折叠成一个正方体； D、是田字格，故不能折叠成一个正方体 故选 A 4. 实数
12、a，b，c，d在数轴上的对应点的位置如图所示，则正确的结论是（ ） A. a4 B. bd0 C. |a|d| D. b+c0 【答案】C 【解析】 【分析】根据数轴上点的位置关系，可得 a，b，c，d的大小，根据有理数的运算，绝对值的性质，可得答案 【详解】解：由数轴上点的位置，得 a4b0c1d A、a4，故 A不符合题意； B、bd0，故 B不符合题意； C、|a|4=|d|，故 C符合题意； D、b+c0，故 D不符合题意； 故选：C 【点睛】本题考查了实数与数轴以及绝对值，观察数轴，能根据点的位置判断点对应的数的大小是解题关键 5. 在0.1428中用数字 3替换其中的一个非 0 数
13、码后，使所得的数最大，则被替换的字是（ ） A. 1 B. 2 C. 4 D. 8 【答案】C 【解析】 【详解】解：逐个代替后这四个数分别为-0.3428，-0.1328，-0.1438，-0.1423 -0.1328 的绝对值最小，只有 C 符合故选 C 6. 下列说法正确的是（ ） A. 12不是整式 B. 2x2y与 y2x是同类项 C. y是单项式 D. 3x2y的次数是 4 【答案】C 【解析】 【分析】根据整式、同类项、单项式及其次数的概念分别判断解答即可 【详解】解：A、12是整式，此选项错误； B、2x2y与 y2x 相同字母的指数不同，不是同类项，此选项错误； C、y 是单
14、项式，此选项正确； D、3x2y 的次数是 2+1=3，此选项错误， 故选：C 【点睛】本题考查整式、同类项的、单项式及其次数，理解相关概念是解答的关键 7. 当 x2 时，代数式 ax3+bx+1的值为 6，那么当 x2 时，这个代数式的值是（ ） A. 1 B. 4 C. 6 D. 5 【答案】B 【解析】 【分析】根据题意可得825ab，再将 x2 代入代数式，即可求解 【详解】解：当 x2时，代数式 ax3+bx+1 的值为 6， 8216ab ， 825ab， 当 x2时，318218215 14axbxabab 故选：B 【点睛】本题主要考查了求代数的值，利用整体代入思想解答是解题
15、的关键 8. 如图，下列说法错误的是( ) A. ECA是一个平角 B. ADE也可以表示为D C. BCA也可以表示为1 D. ABC也可以表示为B 【答案】D 【解析】 【分析】根据平角的定义以及角的表示方法即可得出答案. 【详解】A：ECA是一个平角，故 A 正确； B：ADE也可以表示为D，故 B正确； C：BCA也可以表示为1，故 C 正确； D：点 B处不止一个角，所以ABC不能表示为B，故 D错误； 故答案选择 D 【点睛】本题考查的是平角的定义以及角的表示方法，比较简单，需要熟练掌握角的三种表示方法. 9. 已知AOB=30 ，BOC=45 ，则AOC 等于（ ） A. 15
16、B. 75 C. 15或 75 D. 不能确定 【答案】C 【解析】 【分析】根据题意，由于没有图形，所以位置不确定，应分两种情况讨论：AOB 在BOC 的内部AOB在BOC 的外部，求解即可. 【详解】如图： 当AOB 在BOC 的内部时，AOC=BOCAOB=45 30 =15 ； 当AOB 在BOC 的外部时，AOC=BOC+AOB=45+30=75.故选 C 【点睛】此题主要考查了角的运算与比较，关键是要明确题意，分情况画图解题. 10. 下列说法正确的有（ ） n棱柱有 2n 个顶点，2n条棱， （n+2）个面（n 为不小于 3的正整数） ； 点动成线，线动成面，面动成体； 圆锥的侧
17、面展开图是一个圆； 用平面去截一个正方体，截面的形状可以是三角形、四边形、五边形、六边形 A. 1 个 B. 2 个 C. 3 个 D. 4 个 【答案】B 【解析】 【分析】根据立体图形的特征，点、线、面、体，圆锥的特征，截一个几何体的方法判断即可 【详解】n棱柱有 2n 个顶点，3n条棱， （n+2）个面（n 为不小于 3的正整数） ，原来的说法错误； 点动成线，线动成面，面动成体是正确的； 圆锥的侧面展开图是一个扇形，原来的说法错误； 用平面去截一个正方体，截面的形状可以是三角形、四边形、五边形、六边形是正确的 故说法正确的有 2个 故选：B 【点睛】此题主要考查立体图形的特征，熟练掌握
18、，即可解题. 二、填空题（每小题二、填空题（每小题 3 分，共分，共 18 分）分） 11. 在我校第 8 届校运会跳远比赛中，以 4.00米为标准，若小明跳出了 4.22米，可记做+0.22，那么小东跳出了 3.85 米，记作_ 【答案】0 05 米 【解析】 【分析】首先审清题意，明确正和负所表示的意义以 4.00 米为标准，因为超过 4.00 米记为正数，所以低于 4.00 米记为负数，解答即可 【详解】解：小东跳出了 3.85米，记作0.05米 故答案为0.05 米 考点：正数和负数 12. 如果圆柱的侧面展开图是相邻两边长分别为 6，16的长方形，那么这个圆柱的体积等于_ 【答案】1
19、44 或 384 【解析】 【分析】 分两种情况： 底面周长为 6 高为 16； 底面周长为 16高为 6； 先根据底面周长得到底面半径，再根据圆柱的体积公式计算即可求解 【详解】底面周长为 6高为 16， （62）216=2916=144； 底面周长为 16高为 6， （162）26=646=384 答：这个圆柱的体积可以是 144 或 384 考点：几何体的展开图 13. 第一节课是上午 7：50上课，8：35下课，这节课期间时针转过的角度为_（用度分秒的形式表示） 【答案】22 30 【解析】 【分析】钟表表盘共 360，被分成 12大格，每一个大格是 36012=30，据此即可得到答案
20、. 【详解】上午 7：50 上课，8：35下课，这节课用了 45 分钟， 时针旋转的速度为 36012=30（度/小时） 故时针旋转的角度为 306045=22.5=22 30 故答案为22 30. 【点睛】本题考察额是钟表表盘与角度相关的特征，钟表表盘被分成 12大格，每一大格又被分成 5小格，故表盘共被分成 60 小格，每一小格所对角的度数是 6. 14. 如图定义一种新运算“ ”，如：2 122 12 2；x y2xyx，则（4 2） （1）_ 【答案】0 【解析】 【分析】根据新运算法则进行计算即可 【详解】解：根据题意，4 2=4224=2， （4 2） （1）=2 （1）=22 (
21、 1)2 =0， 故答案为：0 【点睛】本题考查有理数的混合运算，理解新运算法则是解答的关键 15. 如图所示的运算程序中，皆开始输入 x的值为 48，第一次输出的结果是 24，第二次输出的结果是 12，第三次输出的结果是 6，则第 2021 次输出的结果为 _ 【答案】6 【解析】 【分析】根据运算程序计算发现，从第三次开始输出结果有如下规律：奇数次输出 6，偶数次输出 3，以此规律解答即可 【详解】解：根据运算程序，第一次输出的结果是 24，第二次输出的结果是 12，第三次输出的结果是 6，第四次输出的结果是 3，第五次输出的结果是 6，第六次输出的结果是 3， 从第三次开始输出结果有如下
22、规律：奇数次输出 6，偶数次输出 3， 第 2021 次输出的结果为 6， 故答案为：6 【点睛】本题考查数字类规律探究、有理数的乘除法运算，理解题意，正确发现输出结果的变化规律是解答的关键 16. 已知关于 x，y的代数式 ax2+2x+x23y2bx+4y5的值与 x 的取值无关，则 ab=_ 【答案】-3 【解析】 【分析】直接利用多项式与 x无关, 进而得出关于 x的同类项系数和为零, 进而得出答案. 【 详 解 】 解 ： 关 于 ,y 的 代 数 株 式 ax2+2x+x2 3y2 bx+4y 5 的 值 与 x 的 取 值 无 关 , 可 得22(1)(2)345axb xyy的
23、值与 x的取值无关, a+1=0,2-b=0, 解得:a=-1,b=2, 故 a-b=-1-2=-3. 故答案为: -3. 【点睛】本题主要考查合并同类项，注意与 x 无关的条件. 三、解答题（第三、解答题（第 17 小题小题 10 分，第分，第 18 小题小题 8 分，第分，第 19 小题小题 9 分，共分，共 27 分）分） 17. 计算： （1） 57320 ； （2）2124232 【答案】 （1）11； （2）8 【解析】 【分析】 （1）先写成省略括号和的形式，再同号相加，最后计算异号两数相加即可； （2）先计算乘方，除法化为乘法和绝对值化简，再计算乘法，最后简算加法即可； 【详解
24、】 （1）解：原式12 3 201223 11 （2）解：原式114434 1 3822 【点睛】本题考查有理数的混合计算问题，掌握有理数混合运算法则，特别是乘方的计算要看清底数有没有负号是解题关键 18. 先化简，再求值: 22242 523xyxxyyxxy，其中x1,y2 . 【答案】 （1） 25xyy；6. 【解析】 【分析】先化简，再代入求值即可. 【详解】解: （1） 原式=222425 26xyxxyyxxy 25xyy 当1, 2xy 时， 原式= 25 122 6 . 【点睛】本题考查了整式的化简求值问题，注意求值时底数是负数代入时要加上括号. 19. 在方格中依次画出从正
25、面、左面、上面看到如图所示几何体的形状图 【答案】见解析 【解析】 【分析】根据从三个方向看简单组合体的画法解答即可 【详解】解：该几何体的形状图如图所示： 【点睛】本题考查从三个方向看几何体，熟练掌握从三个方向看简单组合体的画法是解答的关键 四、 （第四、 （第 20 小题小题 7分，第分，第 21 小题小题 12 分，共分，共 19 分）分） 20. 如图，已知四点 A，B，C，D，请用直尺按要求完成作图 （1）作射线 AD； （2）作直线 BC； （3）连接 BD，请在 BD上确定点 P，使 AP+CP的值最小，并说明理由 【答案】 （1）见解析； （2）见解析； （3）见解析，理由：两
26、点之间线段最短 【解析】 【分析】 （1）根据射线的定义画出图形即可； （2）根据直线的定义画出图形即可； （3）根据两点之间线段最短，连接AC，交BD于点P 【详解】 （1）作射线AD如图所示； （2）作直线 BC如图所示； （3）连接AC，交BD于点P，这时AP CP最小， 理由：两点之间线段最短 【点睛】本题考查直线、射线、线段的定义作图，掌握两点之间线段最短是解题的关键 21. 一辆货车从货场A出发，向东走 2 千米到达批发部B，继续向东走 1.5 千米到达商场C，又向西走 5.5千米到达超市D，最后回到货场 （1）以货场为原点，以东为正方向，用一个单位长度表示 1千米，你能在数轴上分
27、别表示出货场A，批发部B，商场C，超市D的位置吗？ （2）超市D距离货场A多远？ （3）此货车每千米耗油 0.1 升，每升汽油 6.20元，请计算此货车一共需要多少汽油费？ 【答案】 （1）见解析； （2）超市D距离货场A2千米； （3）一共需要 6.82元 【解析】 【分析】 （1）根据题意画出数轴，如图所示； （2）找出 A与 D之间的距离即可； （3）根据题意列出算式，计算即可. 【详解】解： （1）根据题意画出数轴，如图所示： （2）02 1.5 5.52 AD=2=2 答;超市D距离货场A的距离是 2千米 （3）2 1.55.5211（千米） 11 0.1 6.26.82（元） 答：
28、一共需要 6.82元 故答案为（1）见解析； （2）超市D距离货场A2千米； （3）一共需要 6.82元 【点睛】本题考查了数轴及正数与负数. 关键是正确利用数轴表示出各点的位置. 五五.（本题（本题 8 分）分） 22. 将 7张相同的小长方形纸片（如图 1所示）按图 2所示的方式不重叠的放在长方形 ABCD 内，未被覆盖的部分恰好被分割为两个长方形，面积分别为 S1，S2，已知小长方形纸片的长为 a，宽为 b，且 ab （1）当 a9，b2，AD30时，请求： 长方形 ABCD的面积； S2S1的值 （2）当 AD30 时，请用含 a，b 的式子表示 S2S1的值 【答案】 （1）长方形
29、ABCD 的面积为 510；S2-S148； （2）S2-S1ab+30a120b 【解析】 【分析】 （1）由题意可得 AB=a+4b=17，再利用长方形的面积公式求解即可； 由题图可得面积为 S2的长方形长为 303b，宽为 a；面积为 S1的长方形长为 30a，宽为 4b；然后利用长方形的面积公式进行求解即可； （2）由（1）可得 S1，S2与 a，b的关系，然后求差整理即可得解. 【详解】解： （1）长方形 ABCD 的面积为 ADABAD（a+4b）30 （4 2+9）510； 由题意可得：S2=（303b） a=（303 2） 9=216， S1（30a）4b=（309） 4 2=
30、168， S2-S1216-16848； （2）当 AD30 时， S2S1a（303b）4b（30a）30a3ab120b+4abab+30a120b 【点睛】本题主要考查代数式的应用，解此题的关键在于准确理解图形，通过图形利用代数式表示其面积. 六、 （本题六、 （本题 6 分）分） 23. 观察下列等式，探究其中的规律并解答问题： 112 2+3+432 3+4+5+6+752 4+5+6+7+8+9+10k2 （1）第 4 个等式中，k ； （2）写出第 s个等式： ； （3）写出第 n 个等式： （其中 n 为正整数） 【答案】 （1）7； （2）s+(s+1)+（s+2）+（3s2
31、）=(2s1)2； （3）n+(n+1)+（n+2）+（3n2）=(2n1)2 【解析】 【分析】 （1）根据前三个式子得出规律：结果是奇数的平方即可解答； （2） 根据前三个式子的规律： 每一行的第一个数是行数， 后面是奇数个连续整数的和， 右边是奇数的平方，据此即可写出结果； （3）根据（2）中规律直接写出结果即可 【详解】解： （1）由前三个等式知，第 4 个等式为：4+5+6+7+8+9+1072， k=7， 故答案为：7； （2）由所给等式可知， 第 s 个等式为：s+(s+1)+（s+2）+（3s2）=(2s1)2， 故答案为：s+(s+1)+（s+2）+（3s2）=(2s1)2；
32、 （3）由（2）知，第 n个等式为:n+(n+1)+（n+2）+（3n2）=(2n1)2, 故答案为：n个等式为:n+(n+1)+（n+2）+（3n2）=(2n1)2 【点睛】本题考查数字类规律探究，理解题意，找到等式的规律是解答的关键 七、 （本题七、 （本题 10 分）分） 24. 如图 1，直线 DE 上有一点 O，过点 O 在直线 DE 上方作射线 OC，将一直角三角板 AOB（其中OAB30）的直角顶点放在点 O 处，一条直角边 OA在射线 OD上，另一边 OB在直线 DE上方，将直角三角板绕着点 O按每秒 10的速度逆时针旋转一周，设旋转时间为 t秒 （1）当直角三角板旋转到如图
33、2 的位置时，OA 恰好平分COD，此时，BOC与BOE之间有何数量关系 ； （2）若射线 OC 的位值保持不变，且COE140 在旋转的过程中，是否存在某个时刻，使得射线 OA，OC，OD 中的某一条射线是另两条射线所夹角的角平分线？若存在，请直接写出所有满足题意 t的取值 ，若不存在，请说明理由； 在旋转的过程中，当边 AB 与射线 OE 相交时，如图 3，请直接写出AOCBOE的值 【答案】 （1）BOC=BOE； （2）2、8 和 32；50 【解析】 【分析】 （1）根据角平分线的定义得出AOD=AOC，再根据等角的余角相等即可得出结论； （2）分 OA 平分COD、OC 平分AOD
34、、OD平分AOC三种情况分别列出关于 t在方程，然后解方程即可； 由角的和与差得出AOC=140 AOE、BOE=90 AOE 即可解答 【详解】解： （1）OA平分COD， AOD=AOC， AOB=90 ， BOE+AOD =90 ，BOC+AOC =90 ， BOC=BOE， 故答案为：BOC=BOE； （2）存在， COE=140 ， COD=40 ， 当 OA平分COD时，AOD=AOC=20 ，则 10t=20 ，t=2； 当 OC平分AOD时，AOC=DOC，则 10t40 =40 ，t=8； 当 OD平分AOC时，AOD=DOC，则 360 10t=40 ，t=32， 综上，所
35、有满足题意的 t的取值为 2、8 和 32， 故答案为：2、8和 32； COE=140 ， AOC=COEAOE=140 AOE， AOB=90 ， BOE=90 AOE， AOCBOE=（140 AOE）（90 AOE）=50 ， 故答案为：50 【点睛】本题考查角平分线的性质、余角性质、角度的运算，熟练掌握角平分线的性质，分类讨论的思想运用是解答的关键 八、 （本题八、 （本题 12 分）分） 25. 点 O为数轴的原点，点 A、B 在数轴上的位置如图所示，点 A 表示的数为 5，线段 AB的长为线段 OA长的 1.2倍.点 C在数轴上，M为线段 OC的中点 （1）点 B 表示的数为_
36、（2）若线段 BM 的长为 4.5，则线段 AC 的长为_ （3）若线段 AC的长为 x，求线段 BM的长（用含 x 的式子表示） 【答案】 （1）-1； （2）2或 16； （3）512x或512x. 【解析】 【分析】 （1）首先根据 OA的长求出 AB的长，即可得出 OB的长，然后根据点 B 的位置，即可得出点 B表示的数； （2）需分两种情况进行求解：点 C 在点 B 的左侧和右侧，求出 OM和 OC的长，即可得出 AC 的长； （3）需分两种情况进行求解：点 C 在点 B 的左侧和右侧，求出 OM和 OC的长，即可得出 BM的长. 【详解】 （1）根据题意，得 线段 OA的长为 5，线段 AB的长为 6 故线段 OB的长为 6-5=1 点 B 在原点左侧，点 B表示的数为-1 （2）若点 C在点 B 的左侧，则 OM的长为 5.5，OC的长为 11，AC 的长为 16； 若点 C在点 B的右侧，则 OM的长为 3.5，OC的长为 7，AC的长为 2； 故线段 AC的长为 2 或 16. （3）若点 C在点 B 的左侧，则 OC的长为5x，OM 的长为52x，BM 的长为512x； 若点 C在点 B的右侧，则 OC 的长为5x，OM的长为52x ，BM的长为512x； 故线段 BM 的长为512x或512x. 【点睛】此题主要考查数轴的相关知识，熟练掌握，即可解题.
