1、2022年中考数学一轮复习 04 分式 考点考点 课标要求课标要求 考查角度考查角度 1 分式的分式的 概念概念 了解分式的概念，明确分式与整式的区别，了解分式的概念，明确分式与整式的区别，会确定使分式有意义的字母的取值范围；会确定使分式有意义的字母的取值范围； 会求分式值为零时会求分式值为零时x的值的值 考查分式的意义和分式考查分式的意义和分式值为零的情况常以选值为零的情况常以选择、填空题为主择、填空题为主 2 分式的分式的 运算运算 掌握分式的基本性质，会进行分式的约分、掌握分式的基本性质，会进行分式的约分、通分；能熟练地进行分式的加、减、乘、通分；能熟练地进行分式的加、减、乘、除运算及混
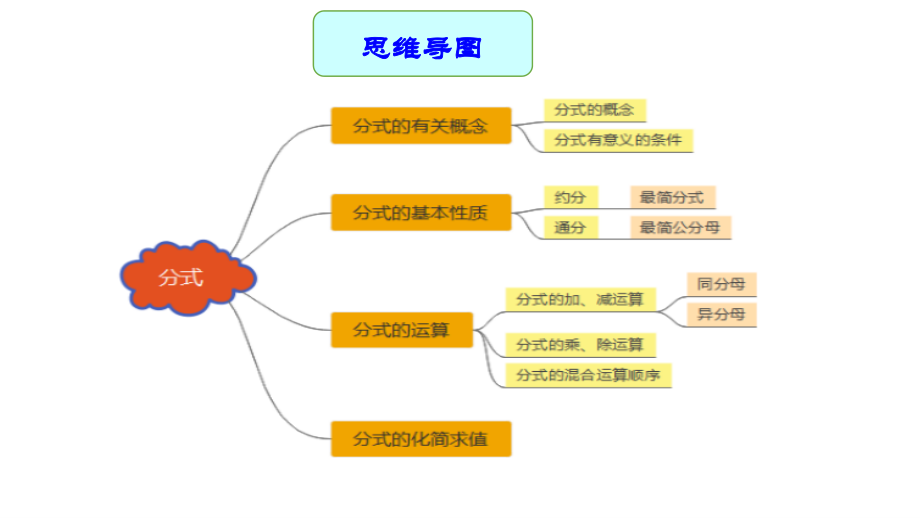
2、合运算，并能解决相关的化简求除运算及混合运算，并能解决相关的化简求值问题值问题 考查分式的基本性质和考查分式的基本性质和分式的运算分式的运算 常以选择、填空题、解常以选择、填空题、解答题的形式命题答题的形式命题 中考命题说明中考命题说明 思维导图思维导图 知识点知识点1 1 ：分式的相关概念分式的相关概念 知识点梳理知识点梳理 1. 分式：分式：如果如果A，B表示两个整式，并且表示两个整式，并且B中含有字母，那么式中含有字母，那么式子子 叫做分式分叫做分式分式式 中，中，A叫做分子，叫做分子，B叫做分母叫做分母 三个条件缺一不可：是形如三个条件缺一不可：是形如 的式子；的式子；A，B为整式；分
3、母为整式；分母B中含有字母中含有字母 特别说明：特别说明： 也可以表示为也可以表示为(a-1)(a+1)，但，但(a-1)(a+1)不是分式，因为它不符合不是分式，因为它不符合 的形式的形式 判断一个式子是不是分式，不能把原式化简后再判断，而只需看原式的本来判断一个式子是不是分式，不能把原式化简后再判断，而只需看原式的本来“面目面目”是否符合分式的定义，与分子中的字母无关比如，是否符合分式的定义，与分子中的字母无关比如， 就是分式就是分式 AB11aa4aaABABAB知识点知识点1 1 ：分式的相关概念分式的相关概念 知识点梳理知识点梳理 2. 有意义的条件：有意义的条件： 分母分母B的值不
4、为的值不为 零零 (B0) . 3. 分式的值为零的条件：分式的值为零的条件： 当分子为当分子为 零零 ，且分母不为零时，分式的值为零，且分母不为零时，分式的值为零(A=0且且B0) 典型例题典型例题 【例【例1】下列式子是分式的是（】下列式子是分式的是（ ） A B C D 【考点】分式的定义【考点】分式的定义 【分析】根据分式的定义逐项判断即可【分析】根据分式的定义逐项判断即可. 【答案】【答案】B . 知识点知识点1 1 ：分式的相关概念分式的相关概念 2x1xx 3x2xy典型例题典型例题 【例【例2】 （3分）（分）（2021河南河南11/23）若代数式）若代数式 有意义，则实数有意
5、义，则实数x的取值范围的取值范围是是 【考点考点】分式有意义的条件分式有意义的条件 【分析分析】分式有意义时分式有意义时，分母分母x- -10，据此求得据此求得x的取值范围的取值范围 【解答解答】解：依题意得：解：依题意得：x- -10， 解得解得x1， 故答案为：故答案为：x1 【点评点评】本题考查了分式有意义的条件本题考查了分式有意义的条件（1）分式有意义的条件是分母不等于零分式有意义的条件是分母不等于零（2）分式无意义的条件是分母等于零分式无意义的条件是分母等于零 知识点知识点1 1 ：分式的相关概念分式的相关概念 11x 典型例题典型例题 【例【例3】（3分）分）（2019北京市北京市
6、9/28）分式）分式 的值为的值为0，则，则x的值是的值是 知识点知识点1 1 ：分式的相关概念分式的相关概念 1xx【考点】分式的值为零的条件【考点】分式的值为零的条件 【分析】根据分式的值为零的条件得到【分析】根据分式的值为零的条件得到x10且且x0，易得，易得x1 【解答】解：【解答】解：分式分式 的值为的值为0， x10且且x0， x1 故答案为故答案为1 【点评】本题考查了分式的值为零的条件：当分式的分母不为零，分子为零时，分式【点评】本题考查了分式的值为零的条件：当分式的分母不为零，分子为零时，分式的值为零的值为零 1xx知识点知识点2 2 ：分式的基本性质分式的基本性质 知识点梳
7、理知识点梳理 1分式的基本性质：分式的基本性质： ， (M为不等于零的整式为不等于零的整式) 2约分：约分：把一个分式的分子与分母的公因式约去，叫做分式的约分把一个分式的分子与分母的公因式约去，叫做分式的约分 3最简分式：最简分式：分子与分母没有分子与分母没有 公因式公因式 的分式叫做最简分式的分式叫做最简分式 AAMBBMAAMBBM知识点知识点2 2 ：分式的基本性质分式的基本性质 知识点梳理知识点梳理 4通分：通分：根据分式的基本性质，把几个异分母的分式分别化成与原来的分式根据分式的基本性质，把几个异分母的分式分别化成与原来的分式 相等相等 的同分母的分式，叫做分式的通分的同分母的分式，
8、叫做分式的通分 5. 最简公分母：最简公分母：几个分式中，各分母的所有因式的最高次幂的积几个分式中，各分母的所有因式的最高次幂的积 6. 变号法则：变号法则： AAAABBBB 知识点知识点2 2 ：分式的基本性质分式的基本性质 典型例题典型例题 【例例4】（3分分）（2020河北河北7/26）若若ab，则下列分式化简正确的是则下列分式化简正确的是（ ） A B C D 22aabb1212aabb22aabb22aabb【考点考点】分式的基本性质分式的基本性质 【分析分析】根据根据ab，可以判断各个选项中的式子是否正确可以判断各个选项中的式子是否正确，从而可以解答本题从而可以解答本题 【解答
9、解答】解：解：ab， ，故选项故选项A错误；错误； ，故选项故选项B错误；错误； ，故选项，故选项C错误；错误； ，故选项，故选项D正确；正确； 故选：故选：D 1212aabb22aabb22aabb22aabb知识点知识点2 2 ：分式的基本性质分式的基本性质 典型例题典型例题 【例【例5】若把分式若把分式 （x，y均不为均不为0）中的）中的x和和y都扩大都扩大3倍，则原分式的值是（倍，则原分式的值是（ ） A扩大扩大3倍倍 B缩小至原来的缩小至原来的 C不变不变 D缩小至原来的缩小至原来的 13163xyxy【分析】若把分式【分析】若把分式 （x，y均不为均不为0）中的）中的x和和y都扩
10、大都扩大3倍，则分子扩大了倍，则分子扩大了339倍，分母的倍，分母的x和和y均扩大均扩大3倍，可用提取公因数法将倍，可用提取公因数法将3提到前面，提到前面，933，故原分式的值扩大了故原分式的值扩大了3倍故选倍故选A 【答案】【答案】A 3xyxy知识点知识点2 2 ：分式的基本性质分式的基本性质 典型例题典型例题 【例【例6】下列分式变形中，正确的是（】下列分式变形中，正确的是（ ） A B C D 22ababab【分析】【分析】A、无法约分，此项不符合题意；、无法约分，此项不符合题意； B、无法约分，此项不符合题意；、无法约分，此项不符合题意； C、当、当m=0是，此时不成立，此项不符合
11、题意；是，此时不成立，此项不符合题意； D、 ，此项符合题意，此项符合题意. 故答案为：故答案为：D. 【答案】【答案】D. 3322()()()()nmnmnmmnnm1xyxy aambbm32()()nmnmmn知识点知识点2 2 ：分式的基本性质分式的基本性质 典型例题典型例题 【例【例7】约分：】约分： =（ ） A B C D 2332415a ba b85ba85ba285ba283ab【分析】【分析】 = = .故答案为故答案为B. 【答案】【答案】B. 2332415a ba b2223 83 5a b ba ab285ba知识点知识点2 2 ：分式的基本性质分式的基本性质
12、典型例题典型例题 【例【例8】已知两个分式：】已知两个分式： ， ，其中，其中x2，则，则A与与B的关的关系是系是（ ） A相等相等 B互为倒数互为倒数 C互为相反数互为相反数 DA大于大于B 244Ax1122Bxx【分析】【分析】 ， ， 故故A-B. 【答案】【答案】C 244(2)(2)4Axxx11112242222(2)(2)(2)(2)xxBxxxxxxxx知识点知识点3 3 ：分式的运算分式的运算 知识点梳理知识点梳理 1分式的乘除法：分式的乘除法： （1）乘法法则：）乘法法则： （2）除法法则：）除法法则： (0)a cacbdb dbdg；(0)aca dadbcdbdb
13、cbcg知识点知识点3 3 ：分式的运算分式的运算 知识点梳理知识点梳理 2分式的加减法：分式的加减法： （1）同分母分式相加减：）同分母分式相加减： （2）异分母分式相加减：）异分母分式相加减： (0)ababcccc；(0)acadbcbdbdbd；知识点知识点3 3 ：分式的运算分式的运算 知识点梳理知识点梳理 3. 分式的乘方：分式的乘方： (n为整数，为整数，b0) 4. 分式的混合运算：分式的混合运算： 在分式的混合运算中，应先算乘方，再将除法化为乘法，进行约分化简，最后在分式的混合运算中，应先算乘方，再将除法化为乘法，进行约分化简，最后进行加减运算，如果有括号，先算括号里面的进行
14、加减运算，如果有括号，先算括号里面的 实数的各种运算律也适用于分式的运算；实数的各种运算律也适用于分式的运算； 分式运算的结果要化成最简分式或整式分式运算的结果要化成最简分式或整式 nnnaabb典型例题典型例题 【例例9】（3分分）（2021江西江西3/23）计算计算 的结果为的结果为（ ） A 1 B - -1 C D 知识点知识点3 3 ：分式的运算分式的运算 11aaa2aa2aa【考点考点】分式的加减法分式的加减法 【分析分析】根据分式的加减运算法则即可求出答案根据分式的加减运算法则即可求出答案 【解答解答】解：原式解：原式= 故选：故选：A 【点评点评】本题考查分式的加减运算本题考
15、查分式的加减运算，解题的关键是熟练运用分式的运算法则解题的关键是熟练运用分式的运算法则，本本题属于基础题型题属于基础题型 1 1=1aaaa 典型例题典型例题 【例【例10】 （3分）（分）（2021包头包头14/26）化简：）化简： 知识点知识点3 3 ：分式的运算分式的运算 2211()422mmmm【考点考点】分式的混合运算分式的混合运算 【分析分析】先把括号内通分先把括号内通分，再把除法运算化为乘法运算再把除法运算化为乘法运算，然后约分即可然后约分即可 【解答解答】解：原式解：原式 故答案为故答案为1 【点评点评】本题考查了分式的混合运算：分式的混合运算本题考查了分式的混合运算：分式的
16、混合运算，要注意运算顺序要注意运算顺序，式与数式与数有相同的混合运算顺序；先乘方有相同的混合运算顺序；先乘方，再乘除再乘除，然后加减然后加减，有括号的先算括号里面的有括号的先算括号里面的 2(2)(2)(2)(2)mmmmm2=12mm典型例题典型例题 【例【例11】 （5分）（分）（2021重庆重庆B卷卷19（2）/26）计算：）计算： 知识点知识点3 3 ：分式的运算分式的运算 22293()211xxxxxx【分析分析】先将被除式分子先将被除式分子、分母因式分解分母因式分解，同时计算括号内分式的加法同时计算括号内分式的加法，再将除法再将除法转化为乘法转化为乘法，继而约分即可继而约分即可
17、【解答】解：原式【解答】解：原式 【点评】本题主要考查分式的混合运算，解题的关键是掌握分式的混合运算顺序及【点评】本题主要考查分式的混合运算，解题的关键是掌握分式的混合运算顺序及其运算法则其运算法则 222(3)(3)3()(1)11xxxxxxxx2(3)(3)3(1)1xxxxx2(3)(3)1(1)3xxxxx31xx典型例题典型例题 【例例12】（6分分）（2020安徽安徽17/23）观察以下等式：观察以下等式： 第第1个等式：个等式： 第第2个等式：个等式： 第第3个等式：个等式： 第第4个等式：个等式： 第第5个等式：个等式： 按照以上规律，解决下列问题：按照以上规律，解决下列问题
18、： （1）写出第）写出第6个等式：个等式： ； （2）写出你猜想的第）写出你猜想的第n个等式：个等式： （用含（用含n的等式表示），并证明的等式表示），并证明 知识点知识点3 3 ：分式的运算分式的运算 121(1)2311321(1)2422521(1)2533721(1)2644921(1)2755典型例题典型例题 【分析】（【分析】（1）根据题目中前）根据题目中前5个等式，可以发现式子的变化特点，从而可以写出个等式，可以发现式子的变化特点，从而可以写出第第6个等式；个等式； （2）把上面发现的规律用字母）把上面发现的规律用字母n表示出来，并运用分式的混合运算法则计算等号表示出来，并运用分
19、式的混合运算法则计算等号的右边的值，进而得到左右相等便可的右边的值，进而得到左右相等便可 【解答】解：（【解答】解：（1）第）第6个等式：个等式： （2）猜想的第）猜想的第n个等式：个等式： 证明：证明：左边左边 右边，右边， 等式成立等式成立 知识点知识点3 3 ：分式的运算分式的运算 1121(1)28662121(1)22nnnn21221122nnnnnnn知识点知识点4 4 ：分式的化简求值分式的化简求值 知识点梳理知识点梳理 1. 分式的化简求值：分式的化简求值：分式通过化简后，代入适当的值解决问题，注意代入的值分式通过化简后，代入适当的值解决问题，注意代入的值要使分式的分母不为要
20、使分式的分母不为0灵活应用分式的基本性质，对分式进行通分和约分，灵活应用分式的基本性质，对分式进行通分和约分，一般要先分解因式化简求值时，一要注意整体思想，二要注意解题技巧，三一般要先分解因式化简求值时，一要注意整体思想，二要注意解题技巧，三要注意代入的值要使分式有意义要注意代入的值要使分式有意义 2. 分式的自选代值：分式的自选代值：分式的化简求值题型中，自选代值多会设分式的化简求值题型中，自选代值多会设“陷阱陷阱”，因此，因此代值时要注意：当分式运算中不含除法运算时，自选字母的值要使原分式的分代值时要注意：当分式运算中不含除法运算时，自选字母的值要使原分式的分母不为母不为0；当分式运算中含
21、有除法运算时，自选字母的值不仅要使原分式的分；当分式运算中含有除法运算时，自选字母的值不仅要使原分式的分母不为母不为0，还要使除式不为，还要使除式不为0 典型例题典型例题 【例【例13】（6分）（分）（2021通辽通辽19/26）先化简，再求值：）先化简，再求值： ，其中其中x满足满足x2- -x- -2=0 知识点知识点4 4 ：分式的化简求值分式的化简求值 2212(1)121xxxxxx【分析分析】根据分式的混合运算法则把原式化简根据分式的混合运算法则把原式化简，利用因式分解法解出方程利用因式分解法解出方程，根据分式有意义的条件确定根据分式有意义的条件确定x的值的值，代入计算即可代入计算
22、即可 【解答解答】解：原式解：原式 =x (x+1) = x2+x， 解方程解方程x2-x-2=0，得得x1=2，x2=-1， x+10，x-1， 当当x=2时时，原式原式=22+2=6 22211 (1)12xxxxx 2(2) (1)12x xxxx典型例题典型例题 【例【例14】（4分）（分）（2021福建福建15/25）已知非零实数）已知非零实数x，y满足满足 ， 则则 的值等于的值等于 知识点知识点4 4 ：分式的化简求值分式的化简求值 1xyx3xyxyxy【解答解答】解：由解：由 得：得：xy+y=x， x-y=xy， 原式原式 =4 故答案为：故答案为：4 【点评点评】本题考查
23、了分式的值本题考查了分式的值，对条件进行化简对条件进行化简，得到得到x-y=xy，把把x-y看作整看作整体体，代入到代数式求值是解题的关键代入到代数式求值是解题的关键 1xyx3xyxyxy4xyxy典型例题典型例题 【例【例15】（4分）（分）（2021鄂尔多斯鄂尔多斯17（2）/24）先化简：）先化简： ，再从再从- -2，0，1，2中选取一个合适的中选取一个合适的x的值代入求值的值代入求值 知识点知识点4 4 ：分式的化简求值分式的化简求值 222444(2)2xxxxxxx【解答解答】解：解：原式原式 x0，2，-2， 当当x=1时，原式时，原式 【点评】本题考查分式化简，重点是分式化
24、简求值时，要注意选取使分式有意义的值【点评】本题考查分式化简，重点是分式化简求值时，要注意选取使分式有意义的值代入计算代入计算 222(2)24=()(2)xxxx xxx224xxxx2(2)(2)xxxxxg12x 13 典型例题典型例题 【例【例16】（3分）分）（2019河北省河北省13/26）如图，若）如图，若x为正整数，则表示为正整数，则表示 的值的点落在（的值的点落在（ ） A段段 B段段 C段段 D段段 知识点知识点4 4 ：分式的化简求值分式的化简求值 22(2)1+441xxxx典型例题典型例题 【分析】将所给分式的分母配方化简，再利用分式加减法化简，根据【分析】将所给分式的分母配方化简，再利用分式加减法化简，根据x为正整为正整数，从所给图中可得正确答案数，从所给图中可得正确答案 【解答】解：【解答】解： 又又x为正整数，为正整数， 故表示故表示 的值的点落在的值的点落在 故选：故选：B 知识点知识点4 4 ：分式的化简求值分式的化简求值 2222(2)1(2)111+441(2)111xxxxxxxxxx 1121xx 22(2)1+441xxxx
