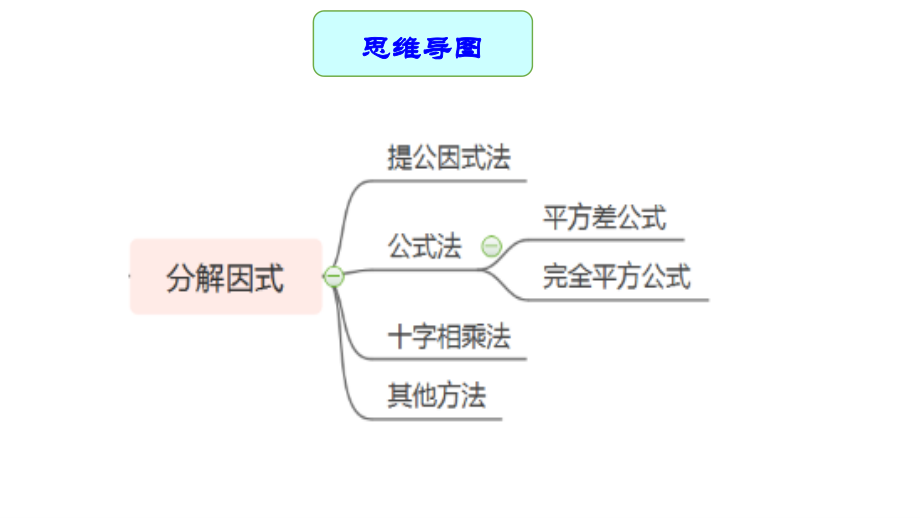
1、2022年中考数学一轮复习 03 因式分解 考点考点 课标要求课标要求 考查角度考查角度 因式因式 分解分解 理解因式分解的概念；理解因式分解的概念； 会用提公因式法、公式法会用提公因式法、公式法等方法进行因式分解等方法进行因式分解 考查因式分解的两种方法考查因式分解的两种方法 以选择题、填空题为主以选择题、填空题为主 中考命题说明中考命题说明 思维导图思维导图 知识点知识点1 1 ：因式分解的因式分解的概念概念 知识点梳理知识点梳理 1. 因式分解的定义：因式分解的定义：把一个多项式化成几个整式的把一个多项式化成几个整式的 乘积乘积 的形式，这的形式，这样的变形叫做把这个多项式样的变形叫做把
2、这个多项式因式分解因式分解也叫做把这个多项式也叫做把这个多项式分解因式分解因式 2. 辨析：辨析：因式分解与整式乘法是相反方向的变形，即互逆运算，二者是一因式分解与整式乘法是相反方向的变形，即互逆运算，二者是一个式子的不同表现形式因式分解的右边是两个或几个因式积的形式，整个式子的不同表现形式因式分解的右边是两个或几个因式积的形式，整式乘法的右边是多项式的形式式乘法的右边是多项式的形式 典型例题典型例题 【例例1】（3分分）（2021呼伦贝尔呼伦贝尔兴安盟兴安盟2/26）下列等式从左到右变形下列等式从左到右变形，属于因属于因式分解的是式分解的是（ ） A(a+b)(a-b)=a2-b2 Bx2-
3、2x+1=(x-1)2 C Dx2+6x+8=x(x+6)+8 知识点知识点1 1 ：因式分解的因式分解的概念概念 121(2)aaa 典型例题典型例题 知识点知识点1 1 ：因式分解的因式分解的概念概念 【解答】解：【解答】解：A、(a+b)(a-b)=a2-b2，原变形是整式乘法，不是因式分解，故此选项，原变形是整式乘法，不是因式分解，故此选项不符合题意；不符合题意； B、x2-2x+1=(x-1)2，把一个多项式化为几个整式的积的形式，原变形是因式分解，把一个多项式化为几个整式的积的形式，原变形是因式分解，故此选项符合题意；故此选项符合题意； C、 ，等式的右边不是几个整式的积的形式，不
4、是因式分解，故，等式的右边不是几个整式的积的形式，不是因式分解，故此选项不符合题意；此选项不符合题意； D、x2+6x+8=x(x+6)+8，等式的右边不是几个整式的积的形式，不是因式分解，故，等式的右边不是几个整式的积的形式，不是因式分解，故此选项不符合题意；此选项不符合题意； 故选：故选：B 121(2)aaa 典型例题典型例题 【例【例2】（】（2020河北河北3/26）对于）对于x-3xy = x(1-3y)，(x+3)(x-1) = x2+2x-3，从左，从左到右的变形，表述正确的是（到右的变形，表述正确的是（ ） A都是因式分解都是因式分解 B都是乘法运算都是乘法运算 C是因式分解
5、，是乘法运算是因式分解，是乘法运算 D是乘法运算，是因式分解是乘法运算，是因式分解 知识点知识点1 1 ：因式分解的因式分解的概念概念 典型例题典型例题 x-3xy = x(1-3y)，(x+3)(x-1) = x2+2x-3， 知识点知识点1 1 ：因式分解的因式分解的概念概念 【考点】因式分解【考点】因式分解提公因式法；因式分解的意义；多项式乘多项式提公因式法；因式分解的意义；多项式乘多项式 【分析】根据因式分解的定义（把一个多项式化成几个整式积的形式，叫因式分【分析】根据因式分解的定义（把一个多项式化成几个整式积的形式，叫因式分解，也叫分解因式）判断即可解，也叫分解因式）判断即可 【解答
6、】解：【解答】解：x-3xy = x(1-3y)，从左到右的变形是因式分解；，从左到右的变形是因式分解； (x+3)(x-1) = x2+2x-3，从左到右的变形是整式的乘法，不是因式分解；，从左到右的变形是整式的乘法，不是因式分解； 所以是因式分解，是乘法运算所以是因式分解，是乘法运算 故选：故选：C 【点评】此题考查了因式分解解题的关键是掌握因式分解的定义：把一个多项【点评】此题考查了因式分解解题的关键是掌握因式分解的定义：把一个多项式化为几个整式的积的形式，这种变形叫做把这个多项式因式分解式化为几个整式的积的形式，这种变形叫做把这个多项式因式分解 知识点知识点2 2 ：因式分解的方法与步
7、骤因式分解的方法与步骤 知识点梳理知识点梳理 1. 一般方法：一般方法： （1）提公因式法：）提公因式法： 如果多项式的各项有公因式，可以把这个公因式提取出来，将多项式写成公因式如果多项式的各项有公因式，可以把这个公因式提取出来，将多项式写成公因式与另一个因式的乘积的形式，这种分解因式的方法叫做与另一个因式的乘积的形式，这种分解因式的方法叫做提公因式法提公因式法 用字母表示：用字母表示：mambmcm(abc) 公因式的确定：公因式的确定：取各项系数的最大公约数，取各项相同的因式及其最低次幂取各项系数的最大公约数，取各项相同的因式及其最低次幂 定系数：公因式的系数是多项式各项系数的最大公约数定
8、系数：公因式的系数是多项式各项系数的最大公约数. 定字母：字母取多项式各项中都含有的相同的字母定字母：字母取多项式各项中都含有的相同的字母. 定指数：相同字母的指数取各项中最小的一个，即字母的最低次数定指数：相同字母的指数取各项中最小的一个，即字母的最低次数. 知识点知识点2 2 ：因式分解的方法与步骤因式分解的方法与步骤 知识点梳理知识点梳理 （2）运用公式法：）运用公式法： 利用公式把某些具有特殊形式（如平方差式，完全平方式等）的多项式分解因式，利用公式把某些具有特殊形式（如平方差式，完全平方式等）的多项式分解因式，这种分解因式的方法叫做公式法这种分解因式的方法叫做公式法. a2b2 (a
9、b)(ab) ； a22abb2 (ab)2 （3）十字相乘法：）十字相乘法：x2+(p+q)x+pq=(x+p)(x+q) （4）分组分解法：）分组分解法：先分组，再提公因式或运用公式先分组，再提公因式或运用公式 知识点知识点2 2 ：因式分解的方法与步骤因式分解的方法与步骤 知识点梳理知识点梳理 2. 一般步骤：一般步骤： 一提一提（提公因式）；（提公因式）；二套二套（套公式）；（套公式）；三验三验（检验是否分解彻底）（检验是否分解彻底） 方法总结：方法总结：分解因式前应先分析多项式的特点，一般先提公因式，再套用公分解因式前应先分析多项式的特点，一般先提公因式，再套用公式注意分解因式必须进
10、行到每一个多项式都不能再分解因式为止式注意分解因式必须进行到每一个多项式都不能再分解因式为止 典型例题典型例题 【例例3】（2020海南海南13/22）因式分解：因式分解：x2- -2x = 【考点考点】因式分解因式分解提公因式法提公因式法 【分析分析】原式提取原式提取x即可得到结果即可得到结果 【解答】解：原式【解答】解：原式= x(x- -2)， 故答案为：故答案为：x(x- -2) 【点评点评】此题考查了因式分解此题考查了因式分解提公因式法提公因式法，熟练掌握提取公因式的方法是解本熟练掌握提取公因式的方法是解本题的关键题的关键 知识点知识点2 2 ：因式分解的方法与步骤因式分解的方法与步
11、骤 利用提公因式法分解因式利用提公因式法分解因式 典型例题典型例题 【例【例4】把】把6x3y23x2y2+8x2y3因式分解时，应提的公因式是（因式分解时，应提的公因式是（ ） A3x2y2 B2x2y2 C6x2y2 Dx2y2 【分析】【分析】6x3y23x2y2+8x2y3x2y2（6x+38y） 故把故把6x3y23x2y2+8x2y3因式分解时，应提的公因式是：因式分解时，应提的公因式是：x2y2 故选故选D 【答案】【答案】D 知识点知识点2 2 ：因式分解的方法与步骤因式分解的方法与步骤 利用提公因式法分解因式利用提公因式法分解因式 典型例题典型例题 【例【例5】（3分）（分）
12、（2021江西江西8/23）因式分解：）因式分解：x24y2 【考点】因式分解【考点】因式分解运用公式法运用公式法 【分析】直接运用平方差公式进行因式分解【分析】直接运用平方差公式进行因式分解 【解答】解：【解答】解：x24y2（x+2y）（）（x2y） 【点评】本题考查了平方差公式分解因式，熟记公式结构是解题的关键平方差【点评】本题考查了平方差公式分解因式，熟记公式结构是解题的关键平方差公式：公式：a2b2（a+b）（）（ab） 知识点知识点2 2 ：因式分解的方法与步骤因式分解的方法与步骤 利用平方差公式分解因式利用平方差公式分解因式 典型例题典型例题 【例【例6】下列各式能用完全平方公式
13、进行分解因式的是（】下列各式能用完全平方公式进行分解因式的是（ ） Ax2 1 Bx22x1 Cx2x1 Dx24x4 【分析】【分析】A不符合完全平方公式的结构，不能用完全平方公式分解因式；不符合完全平方公式的结构，不能用完全平方公式分解因式； B不符合完全平方公式的结构，不能用完全平方公式分解因式；不符合完全平方公式的结构，不能用完全平方公式分解因式； C不符合完全平方公式的结构，不能完全平方公式分解因式；不符合完全平方公式的结构，不能完全平方公式分解因式； D符合完全平方公式的结构，能用完全平方公式分解因式；符合完全平方公式的结构，能用完全平方公式分解因式；故选故选D 【答案】【答案】D
14、 知识点知识点2 2 ：因式分解的方法与步骤因式分解的方法与步骤 利用完全平方公式分解因式利用完全平方公式分解因式 典型例题典型例题 【例【例7】已知二次三项式】已知二次三项式x2+bx+c分解因式为（分解因式为（x3）（）（x+1），则），则b+c的值为（的值为（ ） A1 B1 C5 D5 【分析】【分析】二次三项式二次三项式x2+bx+c分解因式为（分解因式为（x3）（）（x+1），）， x2+bx+c（x3）（）（x+1）x22x3，b2，c3，故，故b+c5故选故选C 【答案】【答案】C 知识点知识点2 2 ：因式分解的方法与步骤因式分解的方法与步骤 利用十字相乘法分解因式利用十字相
15、乘法分解因式 典型例题典型例题 【例【例8】分解因式：】分解因式：x22x24= 【分析】【分析】 x22x24 （x6）（）（x+4） 【答案】（【答案】（x6）（）（x+4） 知识点知识点2 2 ：因式分解的方法与步骤因式分解的方法与步骤 利用十字相乘法分解因式利用十字相乘法分解因式 典型例题典型例题 【例【例9】因式分解：】因式分解：x2 y2 2x+2y 【分析】利用分组分解法分解，先分别分解前两项和后两项，再提取公因式【分析】利用分组分解法分解，先分别分解前两项和后两项，再提取公因式xy即可即可. 【答案】【答案】x2 y22x+2y = (x2 y2 )( 2x2y ) = ( x
16、+y ) ( x y ) 2 ( xy ) = ( xy ) ( x+y2 ) 知识点知识点2 2 ：因式分解的方法与步骤因式分解的方法与步骤 利用分组分解法分解因式利用分组分解法分解因式 典型例题典型例题 【例例10】 （3分分）（2021呼和浩特呼和浩特11/24）因式分解：因式分解：x3y- -4xy= 【考点考点】提公因式法与公式法的综合运用提公因式法与公式法的综合运用 【分析分析】先提取公因式先提取公因式xy，再利用平方差公式对因式再利用平方差公式对因式x2-4进行分解进行分解 【解答解答】解：解：x3y-4xy= xy(x2-4)= xy(x+2)(x-2) 【点评点评】本题是考查
17、学生对分解因式的掌握情况本题是考查学生对分解因式的掌握情况因式分解有两步因式分解有两步，第一步提取公第一步提取公因式因式xy，第二步再利用平方差公式对因式第二步再利用平方差公式对因式x2-4进行分解进行分解，得到结果得到结果xy(x+2)(x-2)，在在作答试题时作答试题时，许多学生分解不到位许多学生分解不到位，提取公因式不完全提取公因式不完全，或者只提取了公因式或者只提取了公因式 知识点知识点2 2 ：因式分解的方法与步骤因式分解的方法与步骤 几种方法的综合运用几种方法的综合运用 典型例题典型例题 【例例11】（2分分）（2021北京北京10/28）分解因式：分解因式：5x25y2 【考点】提公因式法与公式法的综合运用【考点】提公因式法与公式法的综合运用 【分析】提公因式后再利用平方差公式即可【分析】提公因式后再利用平方差公式即可 【解答】解：原式【解答】解：原式5（x2y2）5（x+y）（）（xy），）， 故答案为：故答案为：5（x+y）（）（xy） 【点评】本题考查提公因式法、公式法分解因式，掌握平方差公式的结构特征是【点评】本题考查提公因式法、公式法分解因式，掌握平方差公式的结构特征是正确应用的前提正确应用的前提 知识点知识点2 2 ：因式分解的方法与步骤因式分解的方法与步骤 几种方法的综合运用几种方法的综合运用
