1、考题4：一元一次方程综合一、单选题1（2021·江苏泗阳·七年级期末）某种商品每件的标价是270元，按标价的八折销售时，仍可获利20%，则这种商品每件的进价为（）A180元B200元C225元D259.2元2（2021·江苏·江阴市周庄中学七年级期末）某车间有26名工人，每人每天可以生产800个螺钉或1000个螺母，1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配套设安排x名工人生产螺钉，则下面所列方程正确的是（ ）A2×1000（26x）=800xB1000（13x）=800xC1000（26x）=2×800xD1000（26
2、x）=800x3（2021·江苏医药高新技术产业开发区·七年级期末）若是关于x的方程的解，则m的值为( )ABCD04（2021·江苏海安·七年级期末）小明在某月的日历中圈出了三个数，算出它们的和是14，那么这三个数的位置可能是（ ）ABCD5（2021·江苏东台·七年级期末）某品牌服装店一次同时售出两件上衣，每件售价都是150元，若按成本计算，其中一件盈利25%，另一件亏损25%，则这家商店在这次销售过程中（ ）A盈利为0B盈利为20元C亏损为18元D亏损为20元6（2021·江苏·盐城市初级中学七年级期末）一个
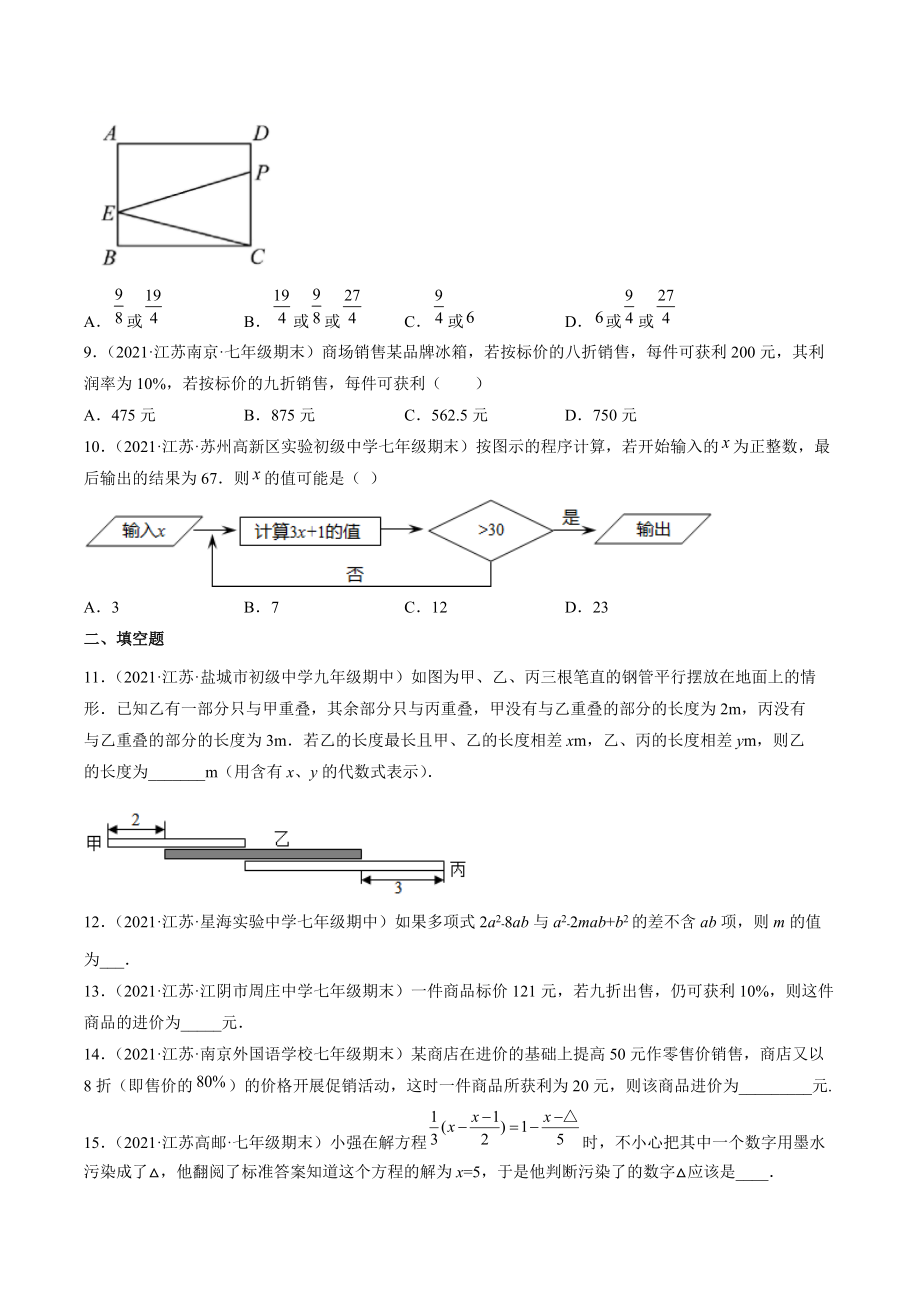
3、长方形的周长为26cm，若这个长方形的长减少3cm，就可成为一个正方形，设这个长方形的长为，可列方程（ ）ABCD7（2021·江苏昆山·七年级期末）若关于的方程的解是，则代数式的值为（ ）ABCD8（2021·江苏昆山·七年级期末）如图，在长方形中，点是上的点，且点从点出发，以的速度沿点匀速运动，最终到达点设点运动时间为，若三角形的面积为，则的值为（ ）A或B或或C或D或或9（2021·江苏南京·七年级期末）商场销售某品牌冰箱，若按标价的八折销售，每件可获利200元，其利润率为10%，若按标价的九折销售，每件可获利（）A475元B8
4、75元C562.5元D750元10（2021·江苏·苏州高新区实验初级中学七年级期末）按图示的程序计算，若开始输入的为正整数，最后输出的结果为67则的值可能是（ ）A3B7C12D23二、填空题11（2021·江苏·盐城市初级中学九年级期中）如图为甲、乙、丙三根笔直的钢管平行摆放在地面上的情形已知乙有一部分只与甲重叠，其余部分只与丙重叠，甲没有与乙重叠的部分的长度为2m，丙没有与乙重叠的部分的长度为3m若乙的长度最长且甲、乙的长度相差xm，乙、丙的长度相差ym，则乙的长度为_m（用含有x、y的代数式表示）12（2021·江苏·星海实验
5、中学七年级期中）如果多项式2a28ab与a22mab+b2的差不含ab项，则m的值为_13（2021·江苏·江阴市周庄中学七年级期末）一件商品标价121元，若九折出售，仍可获利10%，则这件商品的进价为_元14（2021·江苏·南京外国语学校七年级期末）某商店在进价的基础上提高50元作零售价销售，商店又以8折（即售价的）的价格开展促销活动，这时一件商品所获利为20元，则该商品进价为_元.15（2021·江苏高邮·七年级期末）小强在解方程时，不小心把其中一个数字用墨水污染成了，他翻阅了标准答案知道这个方程的解为x=5，于是他判断污染了的
6、数字应该是_16（2021·江苏昆山·七年级期末）在数的学习中，我们会对其中一些具有某种特质的数进行研究，如学习自然数时，我们研究了奇数、偶数、质数、合数等现在我们来研究一种特殊的数巧数定义：若一个两位数恰等于它的各位数字之和的4倍，则这个两位数称为巧数若一个巧数的个位数字比十位数字大，则这个巧数是_17（2021·江苏淮安·七年级期末）一件衣服售价为 200元，现六折销售，仍可获利20%，则这件衣服的进价是_元18（2021·江苏射阳·七年级期末）如果是关于的方程的解，那么的值是_19（2021·江苏东台·七年级
7、期末）我们知道，无限循环小数都可以转化为分数例如：将转化为分数时，可设，由，可知，即，解方程得，即仿此方法，将化成分数是_20（2021·江苏东台·七年级期末）若与是同类项，则的值为_三、解答题21（2021·江苏洪泽·七年级期末）中国古代入民很早就在生产生活中发现了许多有趣的数学问题，其中孙子算经中有个问题，原文：今有三人共车，二车空；二人共车，九人步，问人与车各几何？译文为：今有若干人乘车，每3人共乘一车，最终剩余2辆车，若每2人共乘一车，最终剩余9个人无车可乘，问共有多少人，多少辆车？22（2021·江苏高邮·七年级期末）学习了
8、数学实验手册七（上）钟面上的数学后，小明制作了一个如图所示的模拟钟面，点O为模拟钟面的圆心，钟面上有一条水平线MON，指针OA每秒钟转动24°，指针OB每秒钟转动6°设转动的时间为t秒（t0），AOBn°（0n180），请试着解决下列问题：（1）若指针OA、OB同时从OM开始顺时针旋转当t2秒时，n ；当指针OA从OM旋转到ON的过程中，t 时，指针OB与OA互相垂直；（2）若指针OA从OM开始顺时针转动，同时指针OB从ON开始逆时针转动在OA与OB第二次重合前，求t为何值时n60；在OA与OB第一次重合后、第四次重合前，当t 时，直线MN平分AOB23（2021
9、·江苏·苏州高新区实验初级中学七年级期末）（探索新知）如图1，点将线段分成和两部分，若，则称点是线段的圆周率点，线段、称作互为圆周率伴侣线段（1）若，求的值（用含的代数式表示）；（2）若点也是图1中线段的圆周率点（不同于点），求与的数量关系（深入研究）如图2，现有一个直径为1个单位长度的圆片，将圆片上的某点与数轴上表示1的点重合，并把圆片沿数轴向右无滑动地滚动1周，该点到达点的位置（3）若点、均为线段的圆周率点，求线段的长度；（4）在图2中，点、分别从点、位置同时出发，分别以每秒2个单位长度、每秒1个单位长度的速度向右匀速运动，运动时间为秒点追上点时，停止运动，当、三点中某
10、一点为其余两点所构成线段的圆周率点时，请求出的值24（2021·江苏·仪征市实验初中七年级月考）（阅读理解）我们知道，有理数包括整数、有限小数和无限循环小数，事实上，所有的有理数都 可以化为分数形式（整数可看作分母为1的分数），运用方程思想可以将无限循环小数表 示为分数形式请看以下示例：例1、将 化为分数形式由于，设 则 得，解得 ，于是得 = 例2、将 化为分数形式由于，设 则 得，解得 ，于是得= 根据以上阅读，回答下列问题：（以下计算结果均用最简分数表示）（尝试运用）（1）= ，= ；（思维延伸）写作，像这样的循环小数称为纯循环小数又如、，它们可分别写作、，像这样的循
11、环小数称为混循环小数我们在对混循环小数研究时发现，所有混循环小数都可以先化为纯循环小数，然后再化为分数例如：，请把混循环小数化为分数（视野拓宽）（2）若已知 =，则 = 25（2021·江苏江阴·七年级期中）数轴上有A、B、C三个小球，分别对应的数是a、b、c，且满足a是绝对值最小的正整数，B球在原点的左侧且到原点的距离是5，C球在A球的右侧，且到B球的距离是到A球距离的4倍，三个球都在数轴上同时开始运动，A球向左运动，运动速度为每秒2个单位长度，B、C两球向右运动，运动速度分别为每秒4个单位长度和1个单位长度.（1）a= ；b= ；c= （2）小球A碰到B后按原来的速度立
12、刻返回，B球仍按原速原方向继续前行，请问：小球A在何时何地遇到小球B；当B追上C时停止运动，此时A球所在的位置在哪里？（要有解答过程）（3）在（2）的条件下，整个运动过程中何时三个球中的一个球到另外两个球的距离相等 （直接写出结果）26（2021·江苏南京·七年级期末）以下是两张不同类型火车的车票（“次”表示动车，“次”表示高铁）：（1）根据车票中的信息填空：该列动车和高铁是_向而行（填“相”或“同”）（2）已知该列动车和高铁的平均速度分别为、，两列火车的长度不计经过测算，如果两列火车直达终点（即中途都不停靠任何站点），高铁比动车将早到，求、两地之间的距离在中测算的数据基础
13、上，已知、两地途中依次设有个站点、，且，动车每个站点都停靠，高铁只停靠、两个站点，两列火车在每个停靠站点都停留求该列高铁追上动车的时刻考题4：一元一次方程综合一、单选题1（2021·江苏泗阳·七年级期末）某种商品每件的标价是270元，按标价的八折销售时，仍可获利20%，则这种商品每件的进价为（）A180元B200元C225元D259.2元【标准答案】A【思路点拨】设这种商品每件进价为x元，根据题中的等量关系列方程求解.【精准解析】设这种商品每件进价为x元，则根据题意可列方程270×0.8x0.2x，解得x180.故选A.【名师指路】本题主要考查一元一次方程的应用，
14、解题的关键是确定未知数，根据题中的等量关系列出正确的方程.2（2021·江苏·江阴市周庄中学七年级期末）某车间有26名工人，每人每天可以生产800个螺钉或1000个螺母，1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配套设安排x名工人生产螺钉，则下面所列方程正确的是（ ）A2×1000（26x）=800xB1000（13x）=800xC1000（26x）=2×800xD1000（26x）=800x【标准答案】C【思路点拨】试题思路点拨：此题等量关系为：2×螺钉总数=螺母总数.据此设未知数列出方程即可【精准解析】.故选C.解：设安排x名工人
15、生产螺钉，则（26-x）人生产螺母，由题意得1000（26-x）=2×800x，故C标准答案正确，考点：一元一次方程.3（2021·江苏医药高新技术产业开发区·七年级期末）若是关于x的方程的解，则m的值为( )ABCD0【标准答案】A【思路点拨】把x=5代入方程计算即可求出m的值【精准解析】把x=5代入方程得：10+3m-1=0，解得：m=-3，故选A.【名师指路】本题考查了一元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值4（2021·江苏海安·七年级期末）小明在某月的日历中圈出了三个数，算出它们的和是14，那么这三个数的位置可能
16、是（ ）ABCD【标准答案】B【思路点拨】日历中的每个数都是整数且上下相邻是7，左右相邻相差是1根据题意可列方程求解【精准解析】解：A、设最小的数是xx+x+7+x+7+1=14x=故本选项错误；B、设最小的数是xx+x+1+x+7=14，x=2故本选项正确C、设最小的数是xx+x+1+x+8=14，x=，故本选项错误D、设最小的数是xx+x+6+x+7=14，x=，故本选项错误故选：B【名师指路】本题考查一元一次方程的应用，需要学生具备理解题意能力，关键知道日历中的每个数都是整数且上下相邻是7，左右相邻相差是15（2021·江苏东台·七年级期末）某品牌服装店一次同时售出两
17、件上衣，每件售价都是150元，若按成本计算，其中一件盈利25%，另一件亏损25%，则这家商店在这次销售过程中（ ）A盈利为0B盈利为20元C亏损为18元D亏损为20元【标准答案】D【思路点拨】设盈利的那件上衣的成本价为x元，亏损的那件上衣的成本为y元，根据利润售价成本价，即可得出关于x（y）的一元一次方程，解之即可得出x（y）的值，再将其代入（150x）（150y）中，即可求出结论【精准解析】设盈利的那件上衣的成本价为x元，亏损的那件上衣的成本为y元，依题意，得：150x25%x，150y25%y，解得：x120，y200，（150x）（150y）（150120）（150200）-20（元）故
18、选：D【名师指路】本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键6（2021·江苏·盐城市初级中学七年级期末）一个长方形的周长为26cm，若这个长方形的长减少3cm，就可成为一个正方形，设这个长方形的长为，可列方程（ ）ABCD【标准答案】A【思路点拨】设这个长方形的长为，则正方形的边长为（x-3）cm，则长方形的宽是（13-x）cm，依据正方形的边长相等列得方程【精准解析】设这个长方形的长为，则正方形的边长为（x-3）cm，则长方形的宽是（13-x）cm，则x-3=13-x故选：A【名师指路】此题考查一元一次方程的实际应用，正方形的性质，正确
19、理解题中长方形和正方形的边长关系是解题的关键7（2021·江苏昆山·七年级期末）若关于的方程的解是，则代数式的值为（ ）ABCD【标准答案】A【思路点拨】将方程的解代回方程得，再整体代入代数式求值即可【精准解析】解：把代入原方程得，即，则故选：A【名师指路】本题考查代数式求值和方程解的定义，解题的关键是掌握方程解的定义，以及利用整体代入的思想求值8（2021·江苏昆山·七年级期末）如图，在长方形中，点是上的点，且点从点出发，以的速度沿点匀速运动，最终到达点设点运动时间为，若三角形的面积为，则的值为（ ）A或B或或C或D或或【标准答案】C【思路点拨】分为三
20、种情况讨论，当点P在CD上，即0t3时，根据三角形的面积公式建立方程求出其解即可；当点P在AD上，即3t7时，由SPCES四边形ABCD SCDPSAPESBCE建立方程求出其解即可；当点P在AE上，即7t9时，由SPCEPEBC18建立方程求出其解即可【精准解析】解：设点P运动的时间为ts，AE=4cm，BE=2cm如图，当0t3时，SPCE×2t×818，解得t（s）；如图，当3t7时，SPCE40SCDPSAPESBCE48×6×（2t-6）×4×（14-2t）×8×2=18解之得：t6（s）；如图，当7t9
21、时，SPCE×8×（182t）18，解得t（s）7，t应舍去综上，当ts或6s时，PCE的面积等于18cm2故选C【名师指路】本题考查了一元一次方程的应用，解题的关键是熟知矩形的性质的运用，三角形的面积公式的运用，根据题意找到数量关系列方程求解9（2021·江苏南京·七年级期末）商场销售某品牌冰箱，若按标价的八折销售，每件可获利200元，其利润率为10%，若按标价的九折销售，每件可获利（）A475元B875元C562.5元D750元【标准答案】A【思路点拨】利用进价利润÷利润率可求出该品牌冰箱的进价，设该品牌冰箱的标价为x元，根据“若按标价的八
22、折销售，每件可获利200元”，即可得出关于x的一元一次方程，解之即可求出x的值，再将其代入（90%x2000）中即可求出结论【精准解析】解：该品牌冰箱的进价为200÷10%2000（元）设该品牌冰箱的标价为x元，依题意得：80%x2000200，解得：x2750，90%x200090%×27502000475（元）故选：A【名师指路】本题考查了一元一次方程的运用，找准等量关系，正确列出一元一次方程是解题的关键10（2021·江苏·苏州高新区实验初级中学七年级期末）按图示的程序计算，若开始输入的为正整数，最后输出的结果为67则的值可能是（ ）A3B7C12
23、D23【标准答案】B【思路点拨】根据运算程序列出方程求得相应的x值，直到x不是正整数为止，然后对比选项即可得出标准答案【精准解析】解：最后输出的结果为67，3x+1=67，解得：x=22；当3x+1=22时，解得：x=7；当3x+1=7时，解得：x=2；当3x+1=2时，解得：x=，开始输入的x为正整数，x=不合题意x的值可能为：2或7或22，故选：B【名师指路】本题考查了代数式求值，读懂题意并正确列出方程是解题的关键二、填空题11（2021·江苏·盐城市初级中学九年级期中）如图为甲、乙、丙三根笔直的钢管平行摆放在地面上的情形已知乙有一部分只与甲重叠，其余部分只与丙重叠，甲
24、没有与乙重叠的部分的长度为2m，丙没有与乙重叠的部分的长度为3m若乙的长度最长且甲、乙的长度相差xm，乙、丙的长度相差ym，则乙的长度为_m（用含有x、y的代数式表示）【标准答案】【思路点拨】设乙的长度为米，则甲的长度为：米；丙的长度为：米，甲与乙重叠的部分长度为：米；乙与丙重叠的部分长度为：米，由图可知：甲与乙重叠的部分长度乙与丙重叠的部分长度乙的长度，列出方程，即可解答【精准解析】解：设乙的长度为米，乙的长度最长且甲、乙的长度相差米，乙、丙的长度相差米，甲的长度为：米；丙的长度为：米，甲与乙重叠的部分长度为：米；乙与丙重叠的部分长度为：米，由图可知：甲与乙重叠的部分长度乙与丙重叠的部分长度
25、乙的长度，乙的长度为：米，故标准答案为：【名师指路】本题考查了考查了列代数式，解决本题的关键是根据图形表示出长度，找到等量关系，列方程12（2021·江苏·星海实验中学七年级期中）如果多项式2a28ab与a22mab+b2的差不含ab项，则m的值为_【标准答案】4【思路点拨】先根据整式加减法则进行化简，再根据“差不含项”可得一个关于的一元一次方程，解方程即可得【精准解析】解：，因为与的差不含项，所以，解得，故标准答案为：4【名师指路】本题考查了整式的加减以及无关型问题、一元一次方程的应用，熟练掌握运算法则是解题关键13（2021·江苏·江阴市周庄中学七年
26、级期末）一件商品标价121元，若九折出售，仍可获利10%，则这件商品的进价为_元【标准答案】99【思路点拨】此题的等量关系：实际售价=标价的九折=进价×（1+利润率），设未知数，列方程求解即可【精准解析】解：设这件商品的进价为x元，根据题意得（1+10%）x=121×0.9，解得x=99则这件商品的进价为99元故标准答案为99【名师指路】本题考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解14（2021·江苏·南京外国语学校七年级期末）某商店在进价的基础上提高50元作零售价销售，商店又以8折（即
27、售价的）的价格开展促销活动，这时一件商品所获利为20元，则该商品进价为_元.【标准答案】100【思路点拨】设该商品进价为x元，则售价为(x+50)×80%，进一步利用售价-进价=利润列出方程解答即可.【精准解析】设该商品进价为x元，由题意得(x+50)×80%-x=20解得：x=100，即该商品进价为100元，故标准答案为100【名师指路】本题考查了一元一次方程的实际运用，掌握销售问题中基本数量关系是解决问题的关键15（2021·江苏高邮·七年级期末）小强在解方程时，不小心把其中一个数字用墨水污染成了，他翻阅了标准答案知道这个方程的解为x=5，于是他判断
28、污染了的数字应该是_【标准答案】5【思路点拨】用a表示，把x=5代入方程得到一个关于a的一元一次方程，解方程求得a的值【精准解析】解：用a表示，把x=5代入方程得，解得：a=5故标准答案为：5【名师指路】本题主要考查一元一次方程的求解，属于基础题，熟练掌握一元一次方程的计算方法是解题的关键16（2021·江苏昆山·七年级期末）在数的学习中，我们会对其中一些具有某种特质的数进行研究，如学习自然数时，我们研究了奇数、偶数、质数、合数等现在我们来研究一种特殊的数巧数定义：若一个两位数恰等于它的各位数字之和的4倍，则这个两位数称为巧数若一个巧数的个位数字比十位数字大，则这个巧数是_
29、【标准答案】【思路点拨】根据题意，设十位数字为x，则个位上为（x+3），根据巧数的定义列出方程，解方程即可【精准解析】解：根据题意，设十位数字为x，则个位上为（x+3），则，解得：，十位上的数字是3，个位上的数字是3+3=6，这个巧数是36；故标准答案为：36【名师指路】本题考查了一元一次方程，以及巧数的定义，解题的关键是熟练掌握题意，正确列出方程进行解题17（2021·江苏淮安·七年级期末）一件衣服售价为 200元，现六折销售，仍可获利20%，则这件衣服的进价是_元【标准答案】100【思路点拨】设这件衣服的进价是x元，由题意得（1+20%）x=200，求解即可【精准解析】
30、解：设这件衣服的进价是x元，由题意得（1+20%）x=200，解得x=100故标准答案为：100【名师指路】此题考查一元一次方程的实际应用，正确理解题意是解题的关键18（2021·江苏射阳·七年级期末）如果是关于的方程的解，那么的值是_【标准答案】4【思路点拨】把x=-2代入方程得到关于m的方程，求得m的值即可【精准解析】解：把x=-2代入方程得-1+m=3，解得：m=4故标准答案为：4【名师指路】本题考查了一元一次方程的解，方程的解就是能使方程左右两边相等的未知数的值，理解定义是关键19（2021·江苏东台·七年级期末）我们知道，无限循环小数都可以转化
31、为分数例如：将转化为分数时，可设，由，可知，即，解方程得，即仿此方法，将化成分数是_【标准答案】【思路点拨】设，表示出，然后相减解得出关于的一元一次方程，再求解即可【精准解析】解：设，则，即，解方程得，即故标准答案为：【名师指路】本题考查了解一元一次方程，读懂题目信息，理解无限循环小数转化为分数的方法是解题的关键20（2021·江苏东台·七年级期末）若与是同类项，则的值为_【标准答案】-8【思路点拨】根据同类项定义得到2m+7=3，2n-1=5，解方程求出m及n的值代入计算即可【精准解析】解：由题意得2m+7=3，2n-1=5，解得：m=-2，n=3，故标准答案为：-8【名
32、师指路】此题考查同类项的定义，解一元一次方程，有理数的乘方运算，正确掌握同类项的定义列得方程是解题的关键三、解答题21（2021·江苏洪泽·七年级期末）中国古代入民很早就在生产生活中发现了许多有趣的数学问题，其中孙子算经中有个问题，原文：今有三人共车，二车空；二人共车，九人步，问人与车各几何？译文为：今有若干人乘车，每3人共乘一车，最终剩余2辆车，若每2人共乘一车，最终剩余9个人无车可乘，问共有多少人，多少辆车？【标准答案】共有39人，15辆车【思路点拨】设共有x人，根据题意列出方程，求出方程的解即可得到结果【精准解析】解：设共有x人，根据题意得： ，去分母得：2x+123
33、x27，解得：x39， ，则共有39人，15辆车【名师指路】此题考查了一元一次方程的应用，弄清题意是解本题的关键22（2021·江苏高邮·七年级期末）学习了数学实验手册七（上）钟面上的数学后，小明制作了一个如图所示的模拟钟面，点O为模拟钟面的圆心，钟面上有一条水平线MON，指针OA每秒钟转动24°，指针OB每秒钟转动6°设转动的时间为t秒（t0），AOBn°（0n180），请试着解决下列问题：（1）若指针OA、OB同时从OM开始顺时针旋转当t2秒时，n ；当指针OA从OM旋转到ON的过程中，t 时，指针OB与OA互相垂直；（2）若指针OA从OM
34、开始顺时针转动，同时指针OB从ON开始逆时针转动在OA与OB第二次重合前，求t为何值时n60；在OA与OB第一次重合后、第四次重合前，当t 时，直线MN平分AOB【标准答案】（1）36；5；（2）t的值为4或8或16；10【思路点拨】（1）根据路程速度×时间，可分别算出OA和OB运动的角度，再作差即可根据题意，画出图形，找到等量关系，建立等式，再求解，即可（2）根据题意思路点拨，需要分类讨论，第一次相重合；第一次重合后且OA在OB的右侧；第二次相遇前且OA在OB的左侧先分别算出第一次重合，第二次重合，第三次重合，第四次重合的时间和位置，再根据题意，画出图形，进行思路点拨，列等式，进行
35、求解【精准解析】解：（1）当t2时，AOM2×24°48°，BOM2×6°12°，AOBAOMBOM36°即n36故标准答案为：36如图1，由题意可知，AOM24°t，BOM6°t，OAOB，AOB90°，AOBAOMBOM90°，即24t6t90，解得t5（2）由题意可知，AOM24°t，BON6°t，（）第一次重合前，如图2，可得，AOM+60°+BON180°，即24t+60+6t180，解得t4；（）第一次重合后，且OA在OB的右侧时，如
36、图3，可得，AOM60°+BON180°，即24t60+6t180，解得t8；（）第一次重合后，第二次重合前，且OA在OB的左侧时，如图4，可得，AOM+60°+BON180°，即24t360+60+6t180，解得t16；综上，在OA与OB第二次重合前，n60时，t的值为4或8或16分别算出第一次重合，第二次重合，第三次重合，第四次重合的时间和位置，如图5所示，第一次重合时t6，A1ON36°，第二次重合时t18，A2ON108°，第三次重合时t30，OM，OA，OB重合，第四次重合时t42，A3OM72°（）第一次重合后
37、，第二次重合前，如图6所示，此时BONAON，即6°t24°t180°，解得t10；（）当第二次重合后，第三次重合前，从第二次重合后，记时间为t1，如图7所示，此时，BOMAOM，即180°6°t1108°180°（24°t1108°），解得t112，则t12+1830，此时，OA和OB与OM重合，不符合题意，舍去；（）第三次重合后，第四次重合前，记时间为t2，此时BOM6°t2，AOM24°t2，不存在t2使BOMAOM故标准答案为：10【名师指路】本题主要考查一元一次方程的应用，在
38、“钟面”的背景下考查追及，相遇问题；根据题意，进行准确的分类讨论是解题关键23（2021·江苏·苏州高新区实验初级中学七年级期末）（探索新知）如图1，点将线段分成和两部分，若，则称点是线段的圆周率点，线段、称作互为圆周率伴侣线段（1）若，求的值（用含的代数式表示）；（2）若点也是图1中线段的圆周率点（不同于点），求与的数量关系（深入研究）如图2，现有一个直径为1个单位长度的圆片，将圆片上的某点与数轴上表示1的点重合，并把圆片沿数轴向右无滑动地滚动1周，该点到达点的位置（3）若点、均为线段的圆周率点，求线段的长度；（4）在图2中，点、分别从点、位置同时出发，分别以每秒2个单位
39、长度、每秒1个单位长度的速度向右匀速运动，运动时间为秒点追上点时，停止运动，当、三点中某一点为其余两点所构成线段的圆周率点时，请求出的值【标准答案】（1）AB的值为；（2）；（3）线段MN的长度为；（4）或或或【思路点拨】(1)根据线段之间的数量关系代入解答即可；(2)根据线段的圆周率点的定义及相关线段的大小比较即可解题；(3)由题意可知，点C表示的数是+1，设M点离O点近，且OM=x，根据题意可得关于x的一元一次方程，求解即可；(4)根据题意分类讨论计算即可：点P在点C左侧，PC=CQ；点P在点C左侧，PC=CQ；点P在点C、点Q之间，且PC=PQ；点P在点C、点Q之间，且PC=PQ【精准解
40、析】解：（1），；（2）如图，当BD=AC时，BC=AD，即点也是图1中线段的圆周率点，与的数量关系是相等；（3）由题意可知，点C表示的数是+ 1，若点M、N均为线段OC的圆周率点，不妨设M点离O点近，且OM= x，则x + x = + 1解得：x= 1，MN = = + 1 - 1 - 1 = 1；（4）由题意可知，点P、C、Q所表示的数分别为：2t、 + 1、 + 1 +t，当P、C、Q三点中某一点为其余两点所构成线段的圆周率点时，有以下四种情况：如图，点P在点C左侧，PC= CQ，；如图，点P在点C左侧，PC = CQ，；如图，点P在点C、点Q之间，PC= PQ，；如图，点P在点C、点Q
41、之间，PC =PQ，符合题意的有或或或【名师指路】本题考查了一元一次方程在新定义类动点问题中的应用，有一定综合性，通过数形结合并分类讨论，是解题的关键24（2021·江苏·仪征市实验初中七年级月考）（阅读理解）我们知道，有理数包括整数、有限小数和无限循环小数，事实上，所有的有理数都 可以化为分数形式（整数可看作分母为1的分数），运用方程思想可以将无限循环小数表 示为分数形式请看以下示例：例1、将 化为分数形式由于，设 则 得，解得 ，于是得 = 例2、将 化为分数形式由于，设 则 得，解得 ，于是得= 根据以上阅读，回答下列问题：（以下计算结果均用最简分数表示）（尝试运用）
42、（1）= ，= ；（思维延伸）写作，像这样的循环小数称为纯循环小数又如、，它们可分别写作、，像这样的循环小数称为混循环小数我们在对混循环小数研究时发现，所有混循环小数都可以先化为纯循环小数，然后再化为分数例如：，请把混循环小数化为分数（视野拓宽）（2）若已知 =，则 = 【标准答案】（1）；（2）【思路点拨】（1）根据阅读材料设0.=x，方程两边都乘10，转化为10x=3+x，求出其解即可；设0.=y，方程两边都乘100，转化为100y=23+y，求出其解即可；（2）由，得到，再由，计算即可求解【精准解析】解：（1）设0.=x，即x=0.333，将方程两边都×10，得10x=3.33
43、3，即10x=3+0.333，又因为x=0.333，10x=3+x，9x=3，即x=，0.=；设0.=y， 同理：100y=23+y，解得y=；故标准答案为：；（2），故标准答案为：【名师指路】本题考查了解一元一次方程；理解题意，将无限循环小数转化分数的过程，转化为一元一次方程求解是解题的关键25（2021·江苏江阴·七年级期中）数轴上有A、B、C三个小球，分别对应的数是a、b、c，且满足a是绝对值最小的正整数，B球在原点的左侧且到原点的距离是5，C球在A球的右侧，且到B球的距离是到A球距离的4倍，三个球都在数轴上同时开始运动，A球向左运动，运动速度为每秒2个单位长度，B、
44、C两球向右运动，运动速度分别为每秒4个单位长度和1个单位长度.（1）a= ；b= ；c= （2）小球A碰到B后按原来的速度立刻返回，B球仍按原速原方向继续前行，请问：小球A在何时何地遇到小球B；当B追上C时停止运动，此时A球所在的位置在哪里？（要有解答过程）（3）在（2）的条件下，整个运动过程中何时三个球中的一个球到另外两个球的距离相等 （直接写出结果）【标准答案】（1）1， -5， 3； （2）小球A在1秒后在数轴上表示的点遇到小球B；当B追上C时，A球所在的位置在单位长度处；（3），【思路点拨】（1）根据绝对值的应用，数轴上的点的位置确定的值；（2）根据题意，先求得相遇的时间，进而根据速度
45、乘以时间等于路程确定点的位置；（3）设运动时间为，根据题意结合数轴思路点拨三点的运动情况，分类讨论，时，相遇前，当在中间时，当时，相遇，到的距离相等，当时，相遇后，由于的速度比的速度快，当在中间时，当相遇时，到的距离相等，当相遇时，到的距离相等，根据各情况列方程，解方程求解即可【精准解析】（1）a是绝对值最小的正整数， B球在原点的左侧且到原点的距离是5， C球在A球的右侧，且到B球的距离是到A球距离的4倍，解得故标准答案为：（2）A、B相遇时间：（秒）A、B相遇点：，小球A在1秒后在数轴上表示的点遇到小球BB追上C时间：（秒） A的位置：-1+2×（-1）=当B追上C时，A球所在的位置在数轴上表示单位长度处；（3）设运动时间为，时，相遇前，当在中间时，解得当时，相遇，到的距离相等，当时，相遇后，由于的速度比的速度快，当在中间时，解得当相遇时，到的距离相等，解得当相遇时，到的距离相等即解
