 浙江省宁波市鄞州区2021-2022学年七年级上数学期中模拟试卷(含答案)
浙江省宁波市鄞州区2021-2022学年七年级上数学期中模拟试卷(含答案)
《浙江省宁波市鄞州区2021-2022学年七年级上数学期中模拟试卷(含答案)》由会员分享,可在线阅读,更多相关《浙江省宁波市鄞州区2021-2022学年七年级上数学期中模拟试卷(含答案)(12页珍藏版)》请在七七文库上搜索。
1、2021年宁波市鄞州区七年级上期中模拟卷一选择题(共10小题)1若表示一个数的相反数,则这个数是ABC2D2在,四个数中,属于无理数的是ABCD3随着我国金融科技不断发展,网络消费、网上购物已成为人们生活不可或缺的一部分,今年“双十一”天猫成交额高达2684亿元将数据“2684亿”用科学记数法表示ABCD4下列计算正确的是ABCD5下列说法中正确的是A的平方根是B的平方根是C的立方根是D的算术平方根是46若,且,则ABCD37解方程有下列四个步骤,其中变形错误的一步是ABCD8数轴上表示1,的点分别为,点是的中点,则点所表示的数是ABCD9当时,多项式的值为2,则当时,多项式的值为A0BCD1
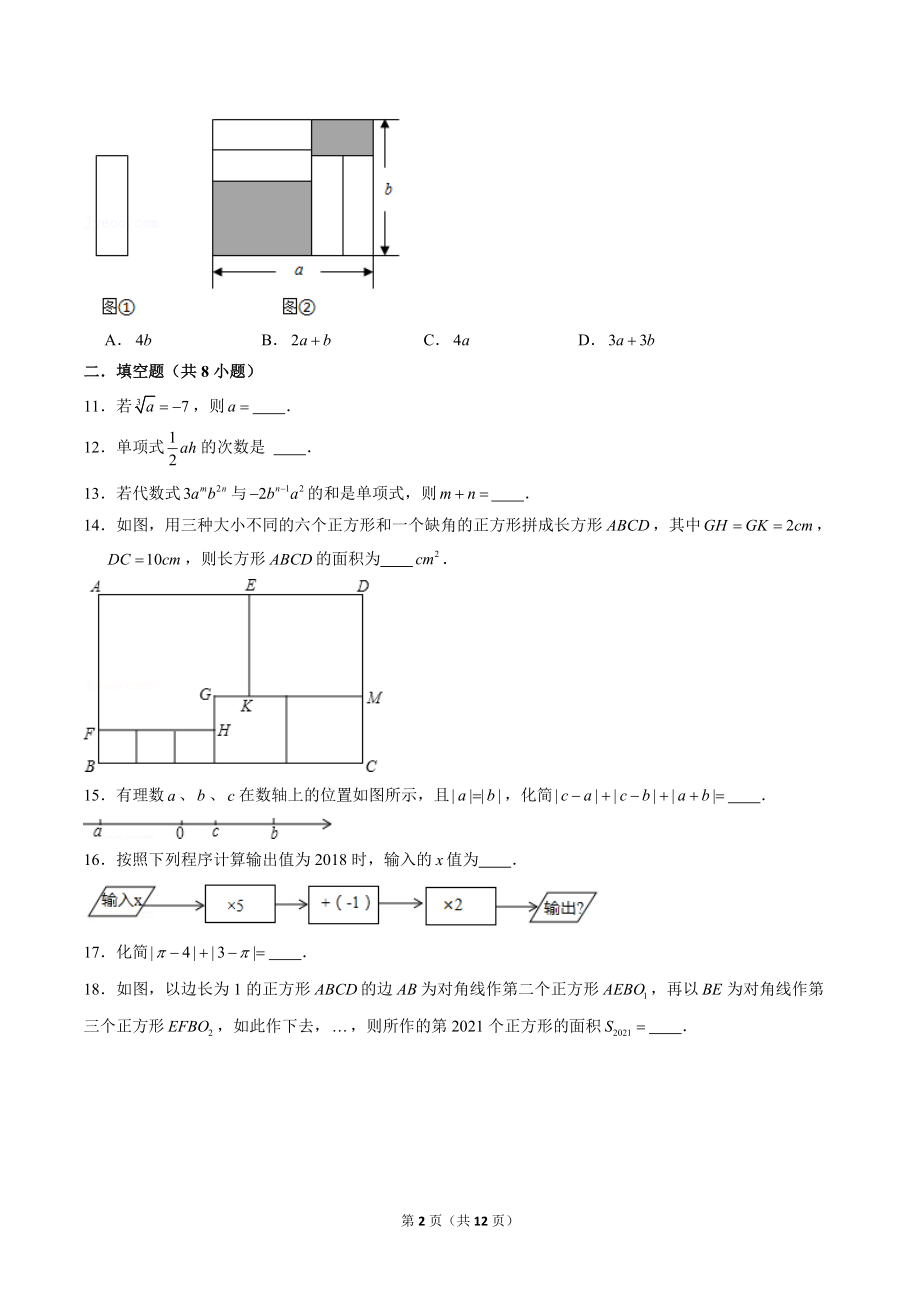
2、0把四张形状大小完全相同的小长方形卡片(如图,卡片长为,宽为,不重叠地放在一个底面为长方形(宽为的盒子底部(如图,盒底面未被卡片覆盖的部分用阴影表示则图中两块阴影部分周长和是(用只含的代数式表示)ABCD二填空题(共8小题)11若,则12单项式的次数是 13若代数式与的和是单项式,则14如图,用三种大小不同的六个正方形和一个缺角的正方形拼成长方形,其中,则长方形的面积为15有理数、在数轴上的位置如图所示,且,化简16按照下列程序计算输出值为2018时,输入的值为17化简18如图,以边长为1的正方形的边为对角线作第二个正方形,再以为对角线作第三个正方形,如此作下去,则所作的第2021个正方形的面
3、积三解答题(共6小题)19计算:(1)(2)20解方程:(1)(2)21先化简,再求值:,其中、满足22如图,某校有一块长为,宽为的长方形场地,学校计划把它的各边长都扩大,作为健身场地(1)用含、的代数式表示扩大部分场地(即阴影部分)的面积;(2)求出当,时阴影部分的面积23先阅读,后探究相关的问题【阅读】表示5与2差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离;可以看作,表示5与的差的绝对值,也可理解为5与两数在数轴上所对应的两点之间的距离(1)如图,先在数轴上画出表示点2.5的相反数的点,再把点向左移动1.5个单位,得到点,则点和点表示的数分别为 和 ,两点间的距离是 ;(
4、2)数轴上表示和的两点和之间的距离表示为 ;如果,那么为 ;(3)若点表示的整数为,则当为 时,与的值相等;(4)要使代数式取最小值时,相应的的取值范围是 24对于实数,我们规定:用符号表示不大于的最大整数,称为的根整数,例如:,(1)仿照以上方法计算:;(2)若,写出满足题意的的整数值如果我们对连续求根整数,直到结果为1为止例如:对10连续求根整数2次,这时候结果为1(3)对120连续求根整数,次之后结果为1(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是参考答案与试题解析一选择题(共10小题)1若表示一个数的相反数,则这个数是ABC2D【解答】解:,2的相反数是:故选:
5、2在,四个数中,属于无理数的是ABCD【解答】解:、是循环小数,属于有理数,故本选项不合题意;、,是整数,属于有理数,故本选项不合题意;、是整数,属于有理数,故本选项不合题意;、是无理数,故本选项符合题意故选:3随着我国金融科技不断发展,网络消费、网上购物已成为人们生活不可或缺的一部分,今年“双十一”天猫成交额高达2684亿元将数据“2684亿”用科学记数法表示ABCD【解答】解:将2684亿用科学记数法表示为:故选:4下列计算正确的是ABCD【解答】解:与不是同类项,所以不能合并,故本选项不合题意;,故本选项不合题意;,正确;,故本选项不合题意故选:5下列说法中正确的是A的平方根是B的平方根


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 浙江省 宁波市 鄞州区 2021 2022 学年 年级 数学 期中 模拟 试卷 答案
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-196851.html