1、2021 年山东省淄博市临淄区中考数学一模试卷年山东省淄博市临淄区中考数学一模试卷 一、选择题（本题共一、选择题（本题共 12 小题，在每小题所给出的四个选项中，只有一个是正确的，请把正确的选项填在下小题，在每小题所给出的四个选项中，只有一个是正确的，请把正确的选项填在下 面的表中每小题面的表中每小题 5 分，满分分，满分 60 分，错选、不选或选出的答案超过一个，均记分，错选、不选或选出的答案超过一个，均记 0 分）分） 18 的倒数是（ ） A B8 C8 D 2 2020 年 6 月 23 日， 北斗三号最后一颗全球组网卫星在西昌卫星发射中心成功发射并顺利进入预定轨道， 它的稳定运行标志
2、着全球四大卫星导航系统之一的中国北斗卫星导航系统全面建成该卫星距离地面约 36000 千米，将数据 36000 用科学记数法表示为（ ） A3.6103 B3.6104 C3.6105 D36104 3下列运算错误的是（ ） A B C D 4已知 3m4，32m4n2若 9nx，则 x 的值为（ ） A8 B4 C2 D 5最近一周，小然每天销售某种装饰品的个数为：11，10，11，13，11，13，15关于这组数据，她得出 如下结果，其中错误的是（ ） A众数是 11 B平均数是 12 C方差是 D中位数是 13 6如图，甲、乙、丙三个图形都是由大小相同的小正方体搭成的几何体的俯视图，小正
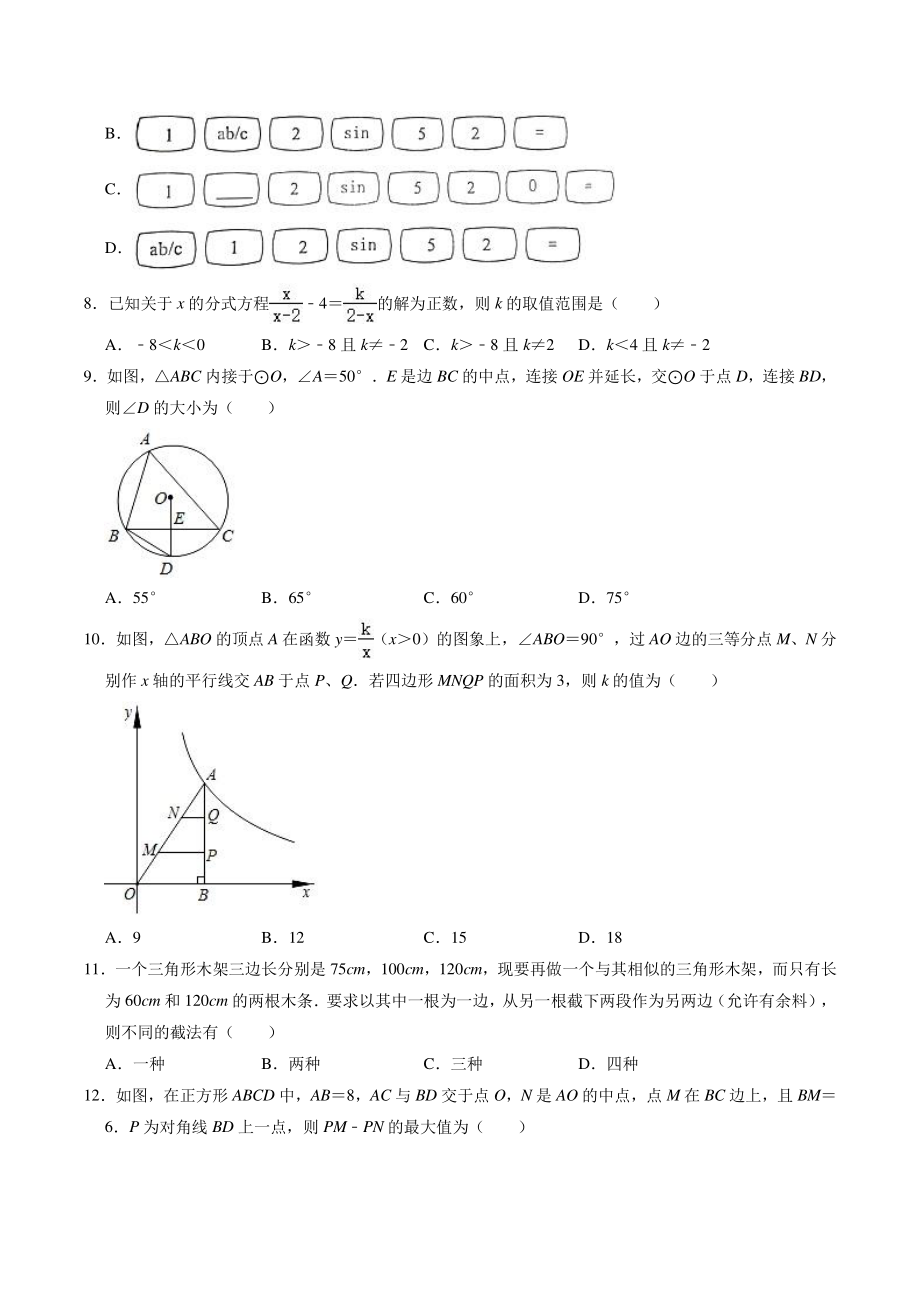
3、方形中的数字表示 该位置小正方体的个数其中主视图相同的是（ ） A仅有甲和乙相同 B仅有甲和丙相同 C仅有乙和丙相同 D甲、乙、丙都相同 7利用我们数学课本上的计算器计算sin52，正确的按键顺序是（ ） A B C D 8已知关于 x 的分式方程4的解为正数，则 k 的取值范围是（ ） A8k0 Bk8 且 k2 Ck8 且 k2 Dk4 且 k2 9如图，ABC 内接于O，A50E 是边 BC 的中点，连接 OE 并延长，交O 于点 D，连接 BD， 则D 的大小为（ ） A55 B65 C60 D75 10如图，ABO 的顶点 A 在函数 y（x0）的图象上，ABO90，过 AO 边的三
4、等分点 M、N 分 别作 x 轴的平行线交 AB 于点 P、Q若四边形 MNQP 的面积为 3，则 k 的值为（ ） A9 B12 C15 D18 11一个三角形木架三边长分别是 75cm，100cm，120cm，现要再做一个与其相似的三角形木架，而只有长 为 60cm 和 120cm 的两根木条要求以其中一根为一边，从另一根截下两段作为另两边（允许有余料）， 则不同的截法有（ ） A一种 B两种 C三种 D四种 12如图，在正方形 ABCD 中，AB8，AC 与 BD 交于点 O，N 是 AO 的中点，点 M 在 BC 边上，且 BM 6P 为对角线 BD 上一点，则 PMPN 的最大值为（
5、 ） A2 B3 C D 二、填空题（每小题二、填空题（每小题 4 分，共分，共 20 分）分） 13已知 a73b，则代数式 a2+6ab+9b2的值为 14若|x2|+0，则xy 15在ABC 中，已知ABC90，BAC30，BC1如图所示，将ABC 绕点 A 按逆时针方向 旋转 90后得到ABC则图中阴影部分的面积为 16甲、乙是两个不透明的纸箱，甲中有三张标有数字，1 的卡片，乙中有三张标有数字 1，2，3 的 卡片，卡片除所标数字外无其他差别，现制定一个游戏规则：从甲中任取一张卡片，将其数字记为 a， 从乙中任取一张卡片，将其数字记为 b若 a，b 能使关于 x 的一元二次方程 ax
6、2+bx+10 有两个不相等 的实数根，则甲获胜；否则乙获胜则乙获胜的概率为 17如图图形都是由同样大小的菱形按照一定规律所组成的，其中第个图形中一共有 3 个菱形，第个 图形中一共有 7 个菱形，第个图形中一共有 13 个菱形，按此规律排列下去，第个图形中菱形的 个数为 三、解答题（第三、解答题（第 18，19 题每题题每题 8 分；第分；第 20，21，22 题每题题每题 10 分，第分，第 23，24 题每题题每题 12 分；满分分；满分 70 分）分） 解答要写出必要的文字说明、证明过程或演算步骤解答要写出必要的文字说明、证明过程或演算步骤. 18解不等式组并写出它的所有整数解 19如
7、图，在ABC 中，M，N 分别是 AB 和 AC 的中点，连接 MN，点 E 是 CN 的中点，连接 ME 并延长， 交 BC 的延长线于点 D若 BC4，则 CD 的长是多少？ 20为了提高学生体质，战胜疫情，某中学组织全校学生宅家一分钟跳绳比赛，全校跳绳平均成绩是每分 钟 99 次，某班班长统计了全班 50 名学生一分钟跳绳成绩，列出的频数分布直方图如图所示，（每个小 组包括左端点，不包括右端点） 求：（1）该班一分钟跳绳的平均次数至少是多少，是否超过全校的平均次数； （2）该班的一个学生说：“我的跳绳成绩是我班的中位数”请你给出该生跳绳成绩的所在范围； （3）从该班中任选一人，其跳绳次数
8、超过全校平均数的概率是多少 21某公司经营甲、乙两种特产，其中甲特产每吨成本价为 10 万元，销售价为 10.5 万元；乙特产每吨成本 价为 1 万元，销售价为 1.2 万元由于受有关条件限制，该公司每月这两种特产的销售量之和都是 100 吨，且甲特产的销售量都不超过 20 吨 （1）若该公司某月销售甲、乙两种特产的总成本为 235 万元，问这个月该公司分别销售甲、乙两种特产 各多少吨？ （2）求该公司一个月销售这两种特产所能获得的最大总利润 22如图，在ABC 的边 BC 上取一点 O，以 O 为圆心，OC 为半径画O，O 与边 AB 相切于点 D，AC AD，连接 OA 交O 于点 E，连
9、接 CE，并延长交线段 AB 于点 F （1）求证：AC 是O 的切线； （2）若 AB10，tanB，求O 的半径； （3）若 F 是 AB 的中点，试探究 BD+CE 与 AF 的数量关系并说明理由 23如图 1，已知四边形 ABCD 是矩形，点 E 在 BA 的延长线上，AEADEC 与 BD 相交于点 G，与 AD 相交于点 F，AFAB （1）求证：BDEC； （2）若 AB1，求 AE 的长； （3）如图 2，连接 AG，求证：EGDGAG 24如图，在直角坐标系中有 RtAOB，O 为坐标原点，OB1，tanABO3，将此三角形绕原点 O 顺时 针旋转 90，得到 RtCOD，二
10、次函数 yx2+bx+c 的图象刚好经过 A，B，C 三点 （1）求二次函数的解析式及顶点 P 的坐标； （2）过定点 Q（1，3）的直线 l：ykxk+3 与二次函数的图象相交于 M，N 两点 若 SPMN2，求 k 的值； 证明：无论 k 为何值，PMN 恒为直角三角形； 当直线 l 绕着定点 Q 旋转时，PMN 外接圆圆心在一条抛物线上运动，直接写出抛物线的表达式 参考答案参考答案 一、选择题（本题共一、选择题（本题共 12 小题，在每小题所给出的四个选项中，只有一个是正确的，请把正确的选项填在下小题，在每小题所给出的四个选项中，只有一个是正确的，请把正确的选项填在下 面的表中每小题面的
11、表中每小题 5 分，满分分，满分 60 分，错选、不选或选出的答案超过一个，均记分，错选、不选或选出的答案超过一个，均记 0 分）分） 18 的倒数是（ ） A B8 C8 D 【分析】根据乘积为 1 的两个数互为倒数，可求一个数的倒数 解：8 的倒数是， 故选：A 2 2020 年 6 月 23 日， 北斗三号最后一颗全球组网卫星在西昌卫星发射中心成功发射并顺利进入预定轨道， 它的稳定运行标志着全球四大卫星导航系统之一的中国北斗卫星导航系统全面建成该卫星距离地面约 36000 千米，将数据 36000 用科学记数法表示为（ ） A3.6103 B3.6104 C3.6105 D36104 【
12、分析】科学记数法的表示形式为 a10n的形式，其中 1|a|10，n 为整数确定 n 的值时，要看把 原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同当原数绝对值10 时，n 是正数；当原数的绝对值1 时，n 是负数 解：360003.6104， 故选：B 3下列运算错误的是（ ） A B C D 【分析】根据分式的基本性质作答，分子分母同时扩大或缩小相同的倍数，分式的值不变，即可得出答 案 解：A、1，故本运算正确； B、 1，故本运算正确； C、 ，故本运算正确； D、 ，故本运算错误； 故选：D 4已知 3m4，32m4n2若 9nx，则 x 的值为（ ） A8
13、B4 C2 D 【分析】根据幂的乘方以及同底数幂的除法法则计算即可求出 n 的值，再根据算术平方根的定义即可求 出 x 的值 解：3m4，32m4n（3m）2（3n）42 42（3n）42， （3n）44228， 又9n32nx， （3n）4（32n）2x2， x28， x 故选：C 5最近一周，小然每天销售某种装饰品的个数为：11，10，11，13，11，13，15关于这组数据，她得出 如下结果，其中错误的是（ ） A众数是 11 B平均数是 12 C方差是 D中位数是 13 【分析】将数据从小到大重新排列，再根据众数、中位数、平均数及方差的定义计算即可 解：将这组数据重新排列为 10，11
14、，11，11，13，13，15， 所以这组数据的众数为 11，中位数为 11，平均数为12， 方差为（1012）2+3（1112）2+2（1312）2+（1512）2， 故选：D 6如图，甲、乙、丙三个图形都是由大小相同的小正方体搭成的几何体的俯视图，小正方形中的数字表示 该位置小正方体的个数其中主视图相同的是（ ） A仅有甲和乙相同 B仅有甲和丙相同 C仅有乙和丙相同 D甲、乙、丙都相同 【分析】由已知条件可知，甲的主视图有 2 列，每列小正方数形数目分别为 2，2；乙的主视图有 2 列， 每列小正方数形数目分别为 2，1；丙的主视图有 2 列，每列小正方数形数目分别为 2，2据此可即可求
15、解 解：根据分析可知，甲的主视图有 2 列，每列小正方数形数目分别为 2，2；乙的主视图有 2 列，每列小 正方数形数目分别为 2，1；丙的主视图有 2 列，每列小正方数形数目分别为 2，2； 则主视图相同的是甲和丙 故选：B 7利用我们数学课本上的计算器计算sin52，正确的按键顺序是（ ） A B C D 【分析】根据计算器的使用方法，可得答案 解：利用该型号计算器计sin52，按键顺序正确的是： ， 故选：B 8已知关于 x 的分式方程4的解为正数，则 k 的取值范围是（ ） A8k0 Bk8 且 k2 Ck8 且 k2 Dk4 且 k2 【分析】表示出分式方程的解，根据解为正数确定出
16、k 的范围即可 解：分式方程4， 去分母得：x4（x2）k， 去括号得：x4x+8k， 解得：x， 由分式方程的解为正数，得到0，且2， 解得：k8 且 k2 故选：B 9如图，ABC 内接于O，A50E 是边 BC 的中点，连接 OE 并延长，交O 于点 D，连接 BD， 则D 的大小为（ ） A55 B65 C60 D75 【分析】连接 CD，根据圆内接四边形的性质得到CDB180A130，根据垂径定理得到 OD BC，求得 BDCD，根据等腰三角形的性质即可得到结论 解：连接 CD， A50， CDB180A130， E 是边 BC 的中点， ODBC， BDCD， ODBODCBDC6
17、5， 故选：B 10如图，ABO 的顶点 A 在函数 y（x0）的图象上，ABO90，过 AO 边的三等分点 M、N 分 别作 x 轴的平行线交 AB 于点 P、Q若四边形 MNQP 的面积为 3，则 k 的值为（ ） A9 B12 C15 D18 【分析】易证ANQAMPAOB，由相似三角形的性质：面积比等于相似比的平方可求出ANQ 的面积，进而可求出AOB 的面积，则 k 的值也可求出 解： NQMPOB， ANQAMPAOB， M、N 是 OA 的三等分点， ， ， 四边形 MNQP 的面积为 3， ， SANQ1， （）2， SAOB9， k2SAOB18， 故选：D 11一个三角形木
18、架三边长分别是 75cm，100cm，120cm，现要再做一个与其相似的三角形木架，而只有长 为 60cm 和 120cm 的两根木条要求以其中一根为一边，从另一根截下两段作为另两边（允许有余料）， 则不同的截法有（ ） A一种 B两种 C三种 D四种 【分析】分类讨论：长 120cm 的木条与三角形木架的最长边相等，则长 120cm 的木条不能作为一边，设 从 120cm 的一根上截下的两段长分别为 xcm，ycm（x+y120），易得长 60cm 的木条不能与 75cm 的一 边对应，所以当长 60cm 的木条与 100cm 的一边对应时有；当长 60cm 的木条与 120cm 的一边对应
19、时有，然后分别利用比例的性质计算出两种情况下得 x 和 y 的值 解：长 120cm 的木条与三角形木架的最长边相等，要满足两边之和大于第三边，则长 120cm 的木条不能 作为一边， 设从 120cm 的木条上截下两段长分别为 xcm，ycm（x+y120）， 由于长 60cm 的木条不能与 75cm 的一边对应，否则 x+y120cm， 当长 60cm 的木条与 100cm 的一边对应，则， 解得：x45，y72； 当长 60cm 的木条与 120cm 的一边对应，则， 解得：x37.5，y50 有两种不同的截法：把 120cm 的木条截成 45cm、72cm 两段或把 120cm 的木条
20、截成 37.5cm、50cm 两 段 故选：B 12如图，在正方形 ABCD 中，AB8，AC 与 BD 交于点 O，N 是 AO 的中点，点 M 在 BC 边上，且 BM 6P 为对角线 BD 上一点，则 PMPN 的最大值为（ ） A2 B3 C D 【分析】以 BD 为对称轴作 N 的对称点 N，连接 MN并延长交 BD 于 P，连 NP，依据 PMPNPM PNMN，可得当 P，M，N三点共线时，取“”，再求得，即可得出 PMABCD， CMN90，再根据NCM 为等腰直角三角形，即可得到 CMMN2 解：如图所示，以 BD 为对称轴作 N 的对称点 N，连接 MN并延长交 BD 于
21、P，连 NP， 根据轴对称性质可知，PNPN， PMPNPMPNMN， 当 P，M，N三点共线时，取“”， 正方形边长为 8， ACAB8， O 为 AC 中点， AOOC4， N 为 OA 中点， ON2， ONCN2， AN6， BM6， CMABBM862， ， PMABCD，CMN90， NCM45， NCM 为等腰直角三角形， CMMN2， 即 PMPN 的最大值为 2， 故选：A 二、填空题（每小题二、填空题（每小题 4 分，共分，共 20 分）分） 13已知 a73b，则代数式 a2+6ab+9b2的值为 49 【分析】先根据完全平方公式变形，再代入，即可求出答案 解：a73b，
22、 a+3b7， a2+6ab+9b2 （a+3b）2 72 49， 故答案为：49 14若|x2|+0，则xy 2 【分析】根据非负数的性质进行解答即可 解：|x2|+0， x20，x+y0， x2，y2， ， 故答案为 2 15在ABC 中，已知ABC90，BAC30，BC1如图所示，将ABC 绕点 A 按逆时针方向 旋转 90后得到ABC则图中阴影部分的面积为 【分析】解直角三角形得到 ABBC，AC2BC2，然后根据扇形的面积公式即可得到结论 解：ABC90，BAC30，BC1， ABBC，AC2BC2， 图中阴影部分面积S 扇形ACCS扇形ADBSABC1 ， 故答案为：； 16甲、乙
23、是两个不透明的纸箱，甲中有三张标有数字，1 的卡片，乙中有三张标有数字 1，2，3 的 卡片，卡片除所标数字外无其他差别，现制定一个游戏规则：从甲中任取一张卡片，将其数字记为 a， 从乙中任取一张卡片，将其数字记为 b若 a，b 能使关于 x 的一元二次方程 ax2+bx+10 有两个不相等 的实数根，则甲获胜；否则乙获胜则乙获胜的概率为 【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果，利用一元二次方程根的判别 式，即可判定各种情况下根的情况，然后利用概率公式求解即可求得乙同学获胜的概率 解：画树状图如下： 由图可知，共有 9 种等可能的结果，其中能使乙同学获胜的有 4 种结
24、果数， 乙同学获胜的概率为， 故答案为： 17如图图形都是由同样大小的菱形按照一定规律所组成的，其中第个图形中一共有 3 个菱形，第个 图形中一共有 7 个菱形，第个图形中一共有 13 个菱形，按此规律排列下去，第个图形中菱形的 个数为 57 【分析】根据图形的变化规律即可得第个图形中菱形的个数 解：第个图形中一共有 3 个菱形，即 2+113； 第个图形中一共有 7 个菱形，即 3+227； 第个图形中一共有 13 个菱形，即 4+3313； ， 按此规律排列下去， 所以第个图形中菱形的个数为：8+7757 故答案为：57 三、解答题（第三、解答题（第 18，19 题每题题每题 8 分；第分
25、；第 20，21，22 题每题题每题 10 分，第分，第 23，24 题每题题每题 12 分；满分分；满分 70 分）分） 解答要写出必要的文字说明、证明过程或演算步骤解答要写出必要的文字说明、证明过程或演算步骤. 18解不等式组并写出它的所有整数解 【分析】分别求出各不等式的解集，再求出其公共解集即可得 解：， 解不等式，x3， 解不等式，得 x， 原不等式组的解集为x3， 它的所有整数解为 0，1，2 19如图，在ABC 中，M，N 分别是 AB 和 AC 的中点，连接 MN，点 E 是 CN 的中点，连接 ME 并延长， 交 BC 的延长线于点 D若 BC4，则 CD 的长是多少？ 【分
26、析】根据三角形中位线定理求出 MN，证明MNEDCE，根据全等三角形的性质解答即可 解：M，N 分别是 AB 和 AC 的中点， MN 是ABC 的中位线， MNBC2，MNBC， NMED，MNEDCE， 点 E 是 CN 的中点， NECE， 在MNE 和DCE 中， ， MNEDCE（AAS）， CDMN2 20为了提高学生体质，战胜疫情，某中学组织全校学生宅家一分钟跳绳比赛，全校跳绳平均成绩是每分 钟 99 次，某班班长统计了全班 50 名学生一分钟跳绳成绩，列出的频数分布直方图如图所示，（每个小 组包括左端点，不包括右端点） 求：（1）该班一分钟跳绳的平均次数至少是多少，是否超过全校
27、的平均次数； （2）该班的一个学生说：“我的跳绳成绩是我班的中位数”请你给出该生跳绳成绩的所在范围； （3）从该班中任选一人，其跳绳次数超过全校平均数的概率是多少 【分析】（1）观察直方图，根据平均数公式计算平均次数后，比较得答案； （2）根据中位数意义，确定中位数的范围； （3）根据频率的计算方法，可得跳绳成绩达到或超过校平均次数的概率为 0.66 解：（1）该班一分钟跳绳的平均次数至少是： 100.8， 100.899， 超过全校的平均次数； （2）这个学生的跳绳成绩在该班是中位数，因为 4+13+1936，所以中位数一定在 100120 范围内； （3）该班一分钟跳绳成绩大于或等于 10
28、0 次的有：19+7+5+233（人）， 故从该班中任选一人，其跳绳次数超过全校平均数的概率是 21某公司经营甲、乙两种特产，其中甲特产每吨成本价为 10 万元，销售价为 10.5 万元；乙特产每吨成本 价为 1 万元，销售价为 1.2 万元由于受有关条件限制，该公司每月这两种特产的销售量之和都是 100 吨，且甲特产的销售量都不超过 20 吨 （1）若该公司某月销售甲、乙两种特产的总成本为 235 万元，问这个月该公司分别销售甲、乙两种特产 各多少吨？ （2）求该公司一个月销售这两种特产所能获得的最大总利润 【分析】（1）根据题意，可以列出相应的一元一次方程，从而可以求得这个月该公司销售甲、
29、乙两种特 产分别为多少吨； （2）根据题意，可以得到利润与甲种特产数量的函数关系式，再根据甲种特产的取值范围和一次函数的 性质，可以得到利润的最大值 解：（1）设销售甲种特产 x 吨，则销售乙种特产（100 x）吨， 10 x+（100 x）1235， 解得，x15， 100 x85， 答：这个月该公司销售甲、乙两种特产分别为 15 吨，85 吨； （2）设利润为 w 万元，销售甲种特产 a 吨， w（10.510）a+（1.21）（100a）0.3a+20， 0a20， 当 a20 时，w 取得最大值，此时 w26， 答：该公司一个月销售这两种特产所能获得的最大总利润是 26 万元 22如图
30、，在ABC 的边 BC 上取一点 O，以 O 为圆心，OC 为半径画O，O 与边 AB 相切于点 D，AC AD，连接 OA 交O 于点 E，连接 CE，并延长交线段 AB 于点 F （1）求证：AC 是O 的切线； （2）若 AB10，tanB，求O 的半径； （3）若 F 是 AB 的中点，试探究 BD+CE 与 AF 的数量关系并说明理由 【分析】（1）连接 OD，由切线的性质可得ADO90，由“SSS”可证ACOADO，可得ADO ACO90，可得结论； （2）由锐角三角函数可设 AC4x，BC3x，由勾股定理可求 BC6，再由勾股定理可求解； （3）连接 OD，DE，由“SAS”可知
31、COEDOE，可得OCEOED，由三角形内角和定理可得 DEF180OECOED1802OCE，DFE180BCFCBF1802 OCE，可得DEFDFE，可证 DEDFCE，可得结论 解：（1）如图，连接 OD， O 与边 AB 相切于点 D， ODAB，即ADO90， AOAO，ACAD，OCOD， ACOADO（SSS）， ADOACO90， ODAB， 又OC 是半径， AC 是O 的切线； （2）tanB， 设 AC4x，BC3x， AC2+BC2AB2， 16x2+9x2100， x2， BC6， ACAD8，AB10， BD2， OB2OD2+BD2， （6OC）2OC2+4，
32、OC， 故O 的半径为； （3）AFCE+BD，理由如下： 连接 OD，DE， 由（1）可知：ACOADO， ACOADO90，AOCAOD， 又CODO，OEOE， COEDOE（SAS）， OCEODE， OCOEOD， OCEOECOEDODE， DEF180OECOED1802OCE， 点 F 是 AB 中点，ACB90， CFBFAF， FCBFBC， DFE180BCFCBF1802OCE， DEFDFE， DEDFCE， AFBFDF+BDCE+BD 23如图 1，已知四边形 ABCD 是矩形，点 E 在 BA 的延长线上，AEADEC 与 BD 相交于点 G，与 AD 相交于点
33、 F，AFAB （1）求证：BDEC； （2）若 AB1，求 AE 的长； （3）如图 2，连接 AG，求证：EGDGAG 【分析】（1）证明AEFADB（SAS），得出AEFADB，证得EGB90，则结论得出； （2）证明AEFDCF，得出，即 AEDFAFDC，设 AEADa（a0），则有 a（a 1）1，化简得 a2a10，解方程即可得出答案； （3） 在线段 EG 上取点 P， 使得 EPDG， 证明AEPADG （SAS） ， 得出 APAG， EAPDAG， 证得PAG 为等腰直角三角形，可得出结论 【解答】（1）证明：四边形 ABCD 是矩形，点 E 在 BA 的延长线上， EA
34、FDAB90， 又AEAD，AFAB， AEFADB（SAS）， AEFADB， GEB+GBEADB+ABD90， 即EGB90， 故 BDEC， （2）解：四边形 ABCD 是矩形， AECD， AEFDCF，EAFCDF， AEFDCF， ， 即 AEDFAFDC， 设 AEADa（a0），则有 a（a1）1，化简得 a2a10， 解得或（舍去）， AE （3）证明：如图，在线段 EG 上取点 P，使得 EPDG， 在AEP 与ADG 中，AEAD，AEPADG，EPDG， AEPADG（SAS）， APAG，EAPDAG， PAGPAD+DAGPAD+EAPDAE90， PAG 为等腰
35、直角三角形， EGDGEGEPPGAG 24如图，在直角坐标系中有 RtAOB，O 为坐标原点，OB1，tanABO3，将此三角形绕原点 O 顺时 针旋转 90，得到 RtCOD，二次函数 yx2+bx+c 的图象刚好经过 A，B，C 三点 （1）求二次函数的解析式及顶点 P 的坐标； （2）过定点 Q（1，3）的直线 l：ykxk+3 与二次函数的图象相交于 M，N 两点 若 SPMN2，求 k 的值； 证明：无论 k 为何值，PMN 恒为直角三角形； 当直线 l 绕着定点 Q 旋转时，PMN 外接圆圆心在一条抛物线上运动，直接写出抛物线的表达式 【分析】（1）根据正切的定义求出 OA，根据
36、旋转变换的性质求出 OC，利用待定系数法求出二次函数 的解析式，利用配方法把一般式化为顶点式，求出顶点 P 的坐标； （2）根据题意求出 PQ1，根据三角形的面积公式得到 x2x14，根据一元二次方程根与系数的关 系解答即可； 根据正切的定义得到 tanPME1x1，tanFPN，进而证明PMEFPN，证明结论； 用 k 表示出 MN 的中点坐标，计算即可 【解答】（1）解：OB1，tanABO3， OAOBtanABO3， A（0，3）， 根据旋转的性质可得：OCOA3， C（3，0）， 根据题意可得：， 解得：， 二次函数的解析式为 yx2+2x+3， yx2+2x+3（x1）2+4， 顶
37、点坐标为 P（1，4）； （2）解：设 M（x1，y1），N（x2，y2）， 直线 l：ykxk+3 过定点 Q（1，3），抛物线的顶点坐标为 P（1，4）， PQ1， SPMNPQ（x2x1）2， x2x14， 联立 yx2+2x+3 与 ykxk+3 可得 x2+（k2）xk0， x1+x22k，x1x2k， （x2x1）2（x1+x2）24x1x2k2+416， k； 证明：过点 P 作 PGx 轴，垂足为 G，分别过点 M，N 作 PG 的垂线，垂足分别为 E、F， 设 M（x1，y1），N（x2，y2） M，N 在二次函数 yx2+2x+3 图象上， y1x12+2x1+3，y2x22+2x2+3 P（1，4）， PE4y14+x122x13（x11）2，ME1x1，PF4y24+x222x23（x21）2，NF x21， tanPME1x1， tanFPN， 由可知 x1+x22k，x1x2k， x1+x22+x1x2， （1x1）（x21）1， 1x1， tanPMEtanFPN， PMEFPN， PME+MPE90， FPN+MPE90，即MPN90， 无论 k 为何值，PMN 恒为直角三角形； 解：设线段 MN 的中点（x，y）， 由可得 MN 的中点为（，）， ， 化简，得 y2x2+4x+1， 抛物线的表达式为 y2x2+4x+1
