 2022年中考数学复习试题:四边形(含答案解析)
2022年中考数学复习试题:四边形(含答案解析)
《2022年中考数学复习试题:四边形(含答案解析)》由会员分享,可在线阅读,更多相关《2022年中考数学复习试题:四边形(含答案解析)(34页珍藏版)》请在七七文库上搜索。
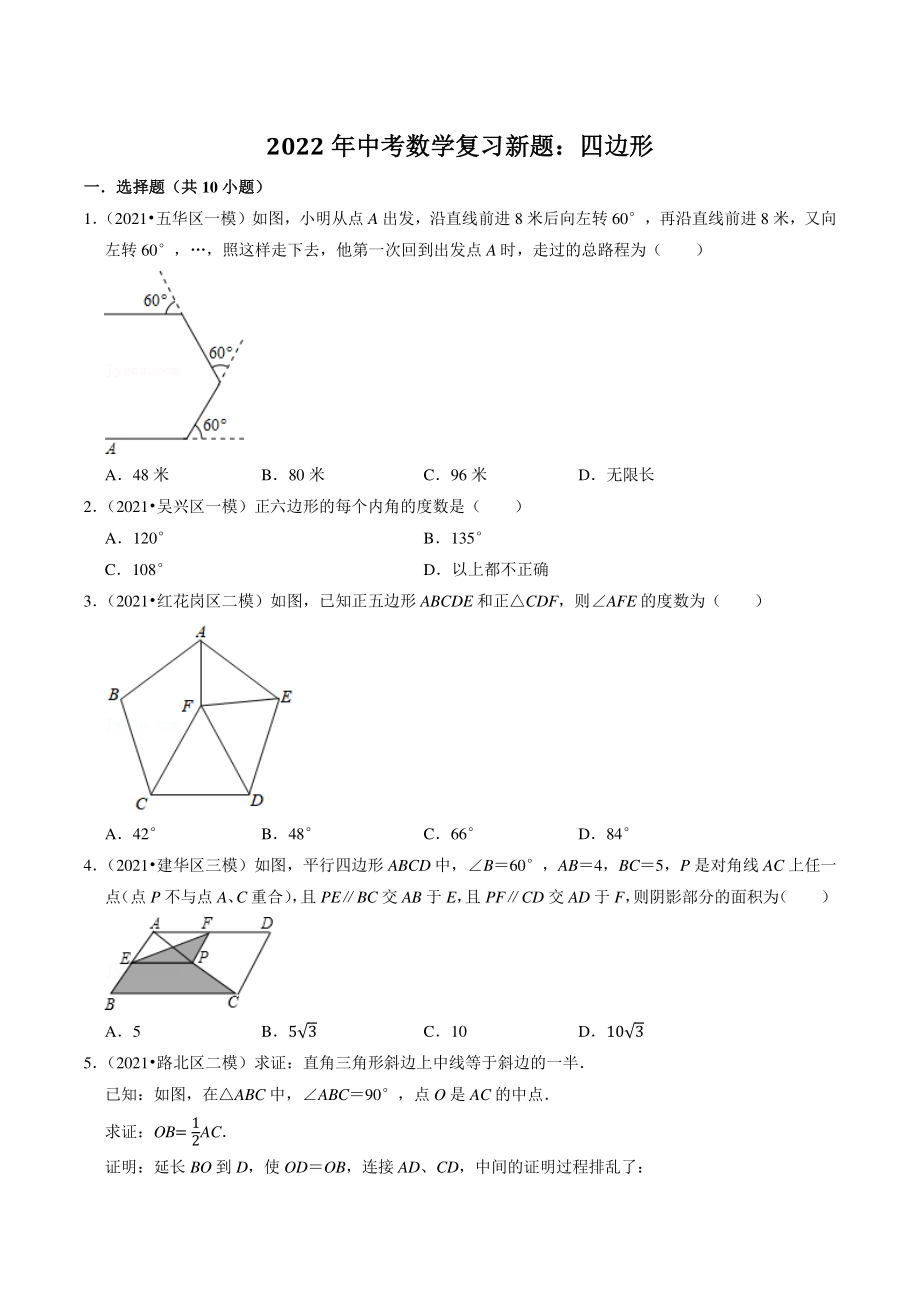
1、 2022 年中考数学复习新题:年中考数学复习新题:四边形四边形 一选择题(共一选择题(共 10 小题)小题) 1 (2021五华区一模)如图,小明从点 A 出发,沿直线前进 8 米后向左转 60,再沿直线前进 8 米,又向 左转 60,照这样走下去,他第一次回到出发点 A 时,走过的总路程为( ) A48 米 B80 米 C96 米 D无限长 2 (2021吴兴区一模)正六边形的每个内角的度数是( ) A120 B135 C108 D以上都不正确 3 (2021红花岗区二模)如图,已知正五边形 ABCDE 和正CDF,则AFE 的度数为( ) A42 B48 C66 D84 4 (2021建
2、华区三模)如图,平行四边形 ABCD 中,B60,AB4,BC5,P 是对角线 AC 上任一 点 (点 P 不与点 A、 C 重合) , 且 PEBC 交 AB 于 E, 且 PFCD 交 AD 于 F, 则阴影部分的面积为 ( ) A5 B53 C10 D103 5 (2021路北区二模)求证:直角三角形斜边上中线等于斜边的一半 已知:如图,在ABC 中,ABC90,点 O 是 AC 的中点 求证:OB= 1 2AC 证明:延长 BO 到 D,使 ODOB,连接 AD、CD,中间的证明过程排乱了: ABC90; ODOB,OAOC; 四边形 ABCD 是平行四边形; 四边形 ABCD 是矩形
3、 ACBD,OB= 1 2BD= 1 2AC 则中间证明过程正确的顺序是( ) A B C D 6 (2021台儿庄区模拟) 如图, 面积为 S 的菱形 ABCD 中, 点 O 为对角线的交点, 点 E 是线段 BC 的中点, 过点 E 作 EFBD 于 F,EGAC 于 G,则四边形 EFOG 的面积为( ) A1 4S B1 8S C 1 12S D 1 16S 7 (2021利辛县二模)如图,RtADG 的斜边和矩形 ABCD 的边 AD 重合,AG、DG 分别交 BC 于点 E、 F,若 AD5,DG3,AE3,则 AB 的长为( ) A1.6 B1.8 C2 D2.4 8 (2021
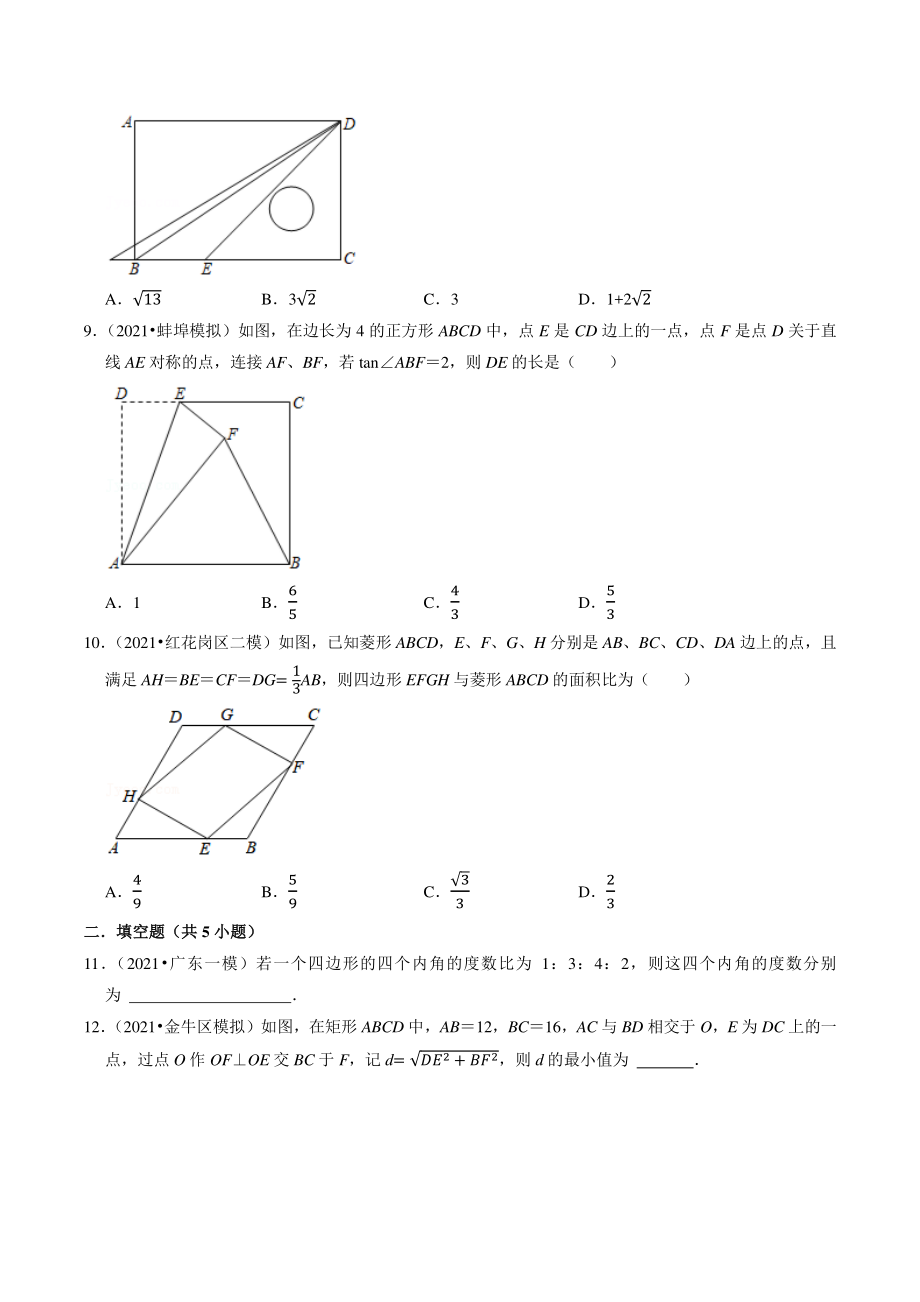
4、延平区模拟)如图,在矩形纸片 ABCD 中,摆放一副三角板,两直角边分别与 BC、CD 重合,若 BE1,ED22,则 BD 的长为( ) A13 B32 C3 D1+22 9 (2021蚌埠模拟)如图,在边长为 4 的正方形 ABCD 中,点 E 是 CD 边上的一点,点 F 是点 D 关于直 线 AE 对称的点,连接 AF、BF,若 tanABF2,则 DE 的长是( ) A1 B6 5 C4 3 D5 3 10 (2021红花岗区二模)如图,已知菱形 ABCD,E、F、G、H 分别是 AB、BC、CD、DA 边上的点,且 满足 AHBECFDG= 1 3AB,则四边形 EFGH 与菱形
5、ABCD 的面积比为( ) A4 9 B5 9 C 3 3 D2 3 二填空题(共二填空题(共 5 小题)小题) 11 (2021广东一模)若一个四边形的四个内角的度数比为 1:3:4:2,则这四个内角的度数分别 为 12 (2021金牛区模拟)如图,在矩形 ABCD 中,AB12,BC16,AC 与 BD 相交于 O,E 为 DC 上的一 点,过点 O 作 OFOE 交 BC 于 F,记 d= 2+ 2,则 d 的最小值为 13 (2021蚌埠二模)如图,在矩形 ABCD 中,AD2AB,点 E 在边 BC 上,连接 AE,DAE 的平分线 AG 与 CD 边交于点 G,与 BC 的延长线交
6、于点 F设 =(0) (1)若 AB2,1,则 CF 的长为 ; (2)连接 EG,若 EGAF,则 的值为 14 (2021嘉鱼县模拟)如图,以矩形 ABCD 的顶点 A 为圆心,AD 长为半径画弧交 BC 于点 F,分别以点 D、F 为圆心,大于1 2DF 长为半径画弧,两弧交于点 P,连接 AP 交 DC 于点 E,连接 EF,若 AE55, 且 tanEFC= 4 3,则 AB 15 (2021太原一模)如图,在ABCD 中,AD6,对角线 BDCD,BAD30,BAD 与CDB 的 平分线交于点 E,延长 DB 到点 F,使 DFAD,连接 EF,则 EF 的长为 三解答题(共三解答
7、题(共 5 小题)小题) 16 (2021交城县二模)综合与实践 问题背景 在综合实践课上,同学们以“图形的平移与旋转”为主题开展数学活动,如图(1) ,先将一张等边三角 形纸片 ABC 对折后剪开,得到两个互相重合的ABD 和EFD,点 E 与点 A 重合,点 B 与点 F 重合, 然后将EFD 绕点 D 顺时针旋转,使点 F 落在边 AB 上,如图(2) ,连接 EC 操作发现 (1)判断四边形 BFEC 的形状,并说明理由; 实践探究 (2)聪聪提出疑问:若等边三角形的边长为 8,将图(2)中的EFD 沿射线 BC 的方向平移 a 个单位 长度,得到EFD,连接 BF,CE,若四边形 B
8、FEC 为菱形,如图(3) ,则 a 的值为多 少?请你帮聪聪解决这个问题,求出 a 的值; (3)如果将(2)中聪聪所提问题的平移方向改为:沿射线 CB 的方向平移 a 个单位长度,其余条件都 不变,则是否还存在四边形 BFEC 为菱形?若存在,直接写出平移距离 a 的值,若不存在,请说明 理由; (4)老师提出问题:请参照聪聪的思路,若等边三角形的边长为 8,将图(2)中的EFD 在平面内进 行一次平移,得到EFD,请在图(4)中画出平移后构造出的新图形,标明字母,说明平移及构 图方法,写出你发现的一个结论,不必证明 17 (2021洪洞县三模)综合与实践 背景阅读: “旋转”即物体绕一个
9、点或一个轴做圆周运动在中国古典专著百喻经口诵乘船法而不解用喻中记 载: “船盘回旋转,不能前进 ”而图形旋转即:在平面内,将一个图形绕一点按某个方向转动一个角度, 这样的运动叫做图形的旋转,这个定点叫做旋转中心,转动的角叫做旋转角综合实践课上, “睿智”小 组专门探究了正方形的旋转,情况如下:在正方形 ABCD 中,点 O 是线段 BC 上的一个动点,将正方形 ABCD 绕点 O 顺时针旋转得到正方形 ABCD(点 A,B,C,D分别是点 A,B,C,D 的对应点) 设 旋转角为 (0180) 操作猜想: (1)如图 1,若点 O 是 BC 中点,在正方形 ABCD 绕点旋转过程中,连接 AA
10、,BB,DD,则线段 AA 与 DD的数量关系是 ;线段 AA与 BB的数量关系是 探究验证: (2)如图 2,在(1)的条件下,在正方形 ABCD 绕点 O 旋转过程中,顺次连接点 B,B,C,C,B判 断四边形 BBCC的形状,并说明理由 拓展延伸: (3) 如图 3, 若 BO2CO, 在正方形 ABCD 绕点 O 顺时针旋转的过程中, 设直线 BB交线段 AA于点 P 连 接OP , 并 过 点O作OQ BB 于 点Q 请 你 补 全 图 形 , 并 直 接 写 出 的 值 18 (2021万柏林区模拟)阅读与思考: 三等分角 古希腊有三大几何问题:立方倍积、三等分角和画圆为方下面是三
11、等分角的作法之一: 如图 1,任意锐角 ABC 可被取作矩形 BCAD 的对角线 BA 与边 BC 的夹角,以 B 为端点的射线交 CA 于 点 E,交 DA 的延长线于点 F,若 EF2AB,则射线 BF 是ABC 的一条三等分线 证明:如图 2,取 EF 的中点 G,连接 AG 四边形 BCAD 是矩形, DAC90,ADBC 在 RtAEF 中,点 G 是 EF 的中点 AG= 1 2EF(依据 1) EF2AB, ABAG ABGAGB(依据 2) 任务一:上面证明过程中的“依据 1” , “依据 2”分别指什么? 依据 1: ; 依据 2: 任务二:完成材料证明中的剩余部分; 任务三
12、:如图 3,矩形 ABCD 中,AB2,对角线 BD 与外角DCF 的平分线交于点 E,若 CE= 1 2BD, 则 CE 的长为 19 (2021万柏林区模拟)主题背景 在课外小组活动中, “创新小组”对“正方形旋转”问题进行了探究 如图 1, 正方形 ABCD 的顶点 A 在正方形 EFGH 的对角线 EG 上, 正方形 EFGH 的顶点 E 是正方形 ABCD 对角线的交点AD 与 EF 相交于点 P,AB 与 EH 相交于点 Q,连接 BF 和 CH 猜想证明 (1)猜想线段 BF 和 CH 有怎样的数量关系和位置关系?并说明理由; 深入探究 (2)如图 2,正方形 EFGH 固定不动
13、,将正方形 ABCD 绕点 E 顺时针方向旋转角 (045) ,延 长 FE,HE 分别交 BC,CD 于点 M,N,连接 MN,NP,PQ,QM,求证:四边形 MNPQ 是正方形; 拓展延伸 (3)已知,正方形 ABCD 的边长为 2,正方形 EFGH 的边长为 3,在正方形 ABCD 旋转过程中,若 BA 的延长线恰好经过点 F,请你直接写出 AP 的长 20 (2021山西模拟)综合与实践 在综合实践活动课上,老师让同学们以“等腰直角三角形的旋转”为主题开展数学活动 问题情境 如图 1,在ABC 中,BAC90,ABAC4,D 为 BC 上一点(0CD 1 2BC) ,将ACD 绕点 A
14、 按顺时针方向旋转,使 AC 与 AB 重合,得到的ABE,过点 E 作 EFBC,交 AB 于点 F过点 F 作 FG BC 于点 G 猜想验证 (1)证明:四边形 BEFG 是正方形; (2)如图 2,延长 EF 交 AC 与点 H,连接 DH,判断四边形 DGFH 的形状,并说明理由; (3)如图 3,AD 与 HF 相交于点 N,若四边形 DGFH 是正方形,请直接写出 FN 的值 2022 年中考数学复习新题速递之四边形(年中考数学复习新题速递之四边形(中考新题汇编中考新题汇编) 参考答案与试题解析参考答案与试题解析 一一选择题(共选择题(共 10 小题)小题) 1 (2021五华区
15、一模)如图,小明从点 A 出发,沿直线前进 8 米后向左转 60,再沿直线前进 8 米,又向 左转 60,照这样走下去,他第一次回到出发点 A 时,走过的总路程为( ) 【解答】解:360606, 8648(米) , 故选:A 2 (2021吴兴区一模)正六边形的每个内角的度数是( ) A120 B135 C108 D以上都不正确 【解答】解:由题意得(62)1806120, 故正六边形的每一个内角度数为 120, 故选:A 3 (2021红花岗区二模)如图,已知正五边形 ABCDE 和正CDF,则AFE 的度数为( ) A42 B48 C66 D84 【解答】解:五边形 ABCDE 是正五边
16、形, EABAEDCDE= (52)180 5 =108,CDDE, CDF 是等边三角形, CDDF, CDF60,DEDF,EAF= 1 2EAB54, EDF1086048, DEF(18048)266, AEF1086642, AFE180AEFEAF180425484, 故选:D 4 (2021建华区三模)如图,平行四边形 ABCD 中,B60,AB4,BC5,P 是对角线 AC 上任一 点 (点 P 不与点 A、 C 重合) , 且 PEBC 交 AB 于 E, 且 PFCD 交 AD 于 F, 则阴影部分的面积为 ( ) A5 B53 C10 D103 【解答】解:四边形 ABC
17、D 是平行四边形, ABCD,ADBC PEBC, PEAD PFCD, PFAB, 四边形 AEPF 为平行四边形, 设AEPF 的对角线 AP、EF 相交于 O,则 AOPO,EOFO,AOEPOF, POFAOE(SAS) , 图中阴影部分的面积等于ABC 的面积, 过 A 作 AMBC 交 BC 于 M, B60,AB4, AM23, SABC= 1 2 523 =53, 即阴影部分的面积等于 53 故选:B 5 (2021路北区二模)求证:直角三角形斜边上中线等于斜边的一半 已知:如图,在ABC 中,ABC90,点 O 是 AC 的中点 求证:OB= 1 2AC 证明:延长 BO 到
18、 D,使 ODOB,连接 AD、CD,中间的证明过程排乱了: ABC90; ODOB,OAOC; 四边形 ABCD 是平行四边形; 四边形 ABCD 是矩形 ACBD,OB= 1 2BD= 1 2AC 则中间证明过程正确的顺序是( ) A B C D 【解答】证明:延长 BO 至点 D,使 ODOB,连接 AD、CD, ODOB,OAOC, 四边形 ABCD 是平行四边形, ABC90, 四边形 ABCD 是矩形, ACBD, OB= 1 2ACBD= 1 2AC, 证明过程正确的顺序是; 故选:D 6 (2021台儿庄区模拟) 如图, 面积为 S 的菱形 ABCD 中, 点 O 为对角线的交
19、点, 点 E 是线段 BC 的中点, 过点 E 作 EFBD 于 F,EGAC 于 G,则四边形 EFOG 的面积为( ) A1 4S B1 8S C 1 12S D 1 16S 【解答】解:四边形 ABCD 是菱形, OAOC,OBOD,ACBD,S= 1 2ACBD, EFBD 于 F,EGAC 于 G, 四边形 EFOG 是矩形,EFOC,EGOB, 点 E 是线段 BC 的中点, EF、EG 都是OBC 的中位线, EF= 1 2OC= 1 4AC,EG= 1 2OB= 1 4BD, 矩形 EFOG 的面积EFEG= 1 4AC 1 4BD= 1 8S; 故选:B 7 (2021利辛县
20、二模)如图,RtADG 的斜边和矩形 ABCD 的边 AD 重合,AG、DG 分别交 BC 于点 E、 F,若 AD5,DG3,AE3,则 AB 的长为( ) A1.6 B1.8 C2 D2.4 【解答】解:在 RtAGD 与 RtEBA 中, ADBF, DAGAEB, BG90, AGDEBA, = , 即 3 = 3 5, AB= 9 5 = 1.8, 故选:B 8 (2021延平区模拟)如图,在矩形纸片 ABCD 中,摆放一副三角板,两直角边分别与 BC、CD 重合,若 BE1,ED22,则 BD 的长为( ) A13 B32 C3 D1+22 【解答】解:由图可知,ECDC, ED2
21、2, ECDC2, BCBE+EC2+13, BD= 2+ 2= 32+ 22= 13, 故选:A 9 (2021蚌埠模拟)如图,在边长为 4 的正方形 ABCD 中,点 E 是 CD 边上的一点,点 F 是点 D 关于直 线 AE 对称的点,连接 AF、BF,若 tanABF2,则 DE 的长是( ) A1 B6 5 C4 3 D5 3 【解答】解:过点 F 作 FNAB 于点 N,并延长 NF 交 CD 于点 M, ABCD, MNCD, FME90, tanABF2, =2, 设 BNx,则 FN2x, AN4x, 点 F 是点 D 关于直线 AE 对称的点, DEEF,DAAF4, A
22、EAE, ADEAFE(SSS) , DAFE90, AN2+NF2AF2, (4x)2+(2x)242, x10(舍) ,x2= 8 5, AN4x4 8 5 = 12 5 ,MF42x4 16 5 = 4 5, EFM+AFNAFN+FAN90, EFMFAN, cosEFMcosFAN, = ,即 4 5 = 12 5 4 , EF= 4 3, DEEF= 4 3 故选:C 10 (2021红花岗区二模)如图,已知菱形 ABCD,E、F、G、H 分别是 AB、BC、CD、DA 边上的点,且 满足 AHBECFDG= 1 3AB,则四边形 EFGH 与菱形 ABCD 的面积比为( ) A4
23、 9 B5 9 C 3 3 D2 3 【解答】解:过点 F 作 MNCD 于点 M,交 AB 的延长线于点 N,如图所示. 四边形 ABCD 是菱形, ABBCCDDA,ABCD,AC,DABC, DMN+ANM180, ANM180DMN1809090, MNAB; 设菱形的边长为 a,则 AHBECFDG= 1 3a,AEBFCGDH= 2 3a, 在AEH 和CGF 中, = = = , AEHCGF(SAS) , SAEHSCGF 同理可证:SBEFSDGH ABCD, = = 1 2, 设 FMh,则 FN2h,MN3h, SBEF= 1 2EBFN= 1 2 1 3a2h= 1 3
24、ah;SCGF= 1 2CGFM= 1 2 2 3ah= 1 3ah, SAEHSBEFSCGFSDGH= 1 3ah, 菱形 ABCD 的面积 S1ABMNa3h3ah, 四边形 EFGH 的面积 S2S14SBEF3ah4 1 3ah= 5 3ah, 2 1 = 5 3 3 = 5 9 故选:B 二填空题(共二填空题(共 5 小题)小题) 11(2021广东一模) 若一个四边形的四个内角的度数比为 1: 3: 4: 2, 则这四个内角的度数分别为 36, 108,144,72 【解答】解:设四边形 4 个内角的度数分别是 x,3x,4x,2x x+3x+4x+2x360, 解得 x36 所

- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2022 年中 数学 复习 试题 四边形 答案 解析
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-195471.html