1、 2022 年中考数学复习新题：年中考数学复习新题：图形的旋转图形的旋转 一选择题（共一选择题（共 10 小题）小题） 1 （2021垦利区一模）随着人们健康生活理念的提高，环保意识也不断增强，以下是回收、绿色包装、节 水、低碳四个标志，其中是中心对称图形的是（ ） ABCD 2 （2021河北模拟）如图是由边长均相等的两个正方形和六个等边三角形组成的图案，现有两个正方形和 一个等边三角形被涂黑，若再有 n 个等边三角形被涂黑，使所有涂黑的新图案既是中心对称图形又是轴 对称图形，则 n 的值是（ ） A4 或 5 B3 或 5 C2 或 3 D1 或 3 3 （2021通城县模拟）在平面直角坐
2、标系中，将点 P（1，2）向右平移 3 个单位长度得到点 P1，则点 P1关于原点的对称点 P2的坐标为（ ） A （2，2） B （2，2） C （2，2） D （3，2） 4（2021春聊城期末） 如图， 在ABC中， BAC138， 将ABC绕点A按逆时针方向旋转得到ABC 若 点 B刚好落在 BC 边上，且 ABCB，则C 的度数为（ ） A13 B14 C15 D16 5 （2021 春万山区期末）如图所示，将AOB 绕点 O 按逆时针方向旋转 45后得到AOB，若AOB 15，那么AOB的度数是（ ） A15 B30 C45 D60 6 （2021福建模拟）已知ABC 是以 AB
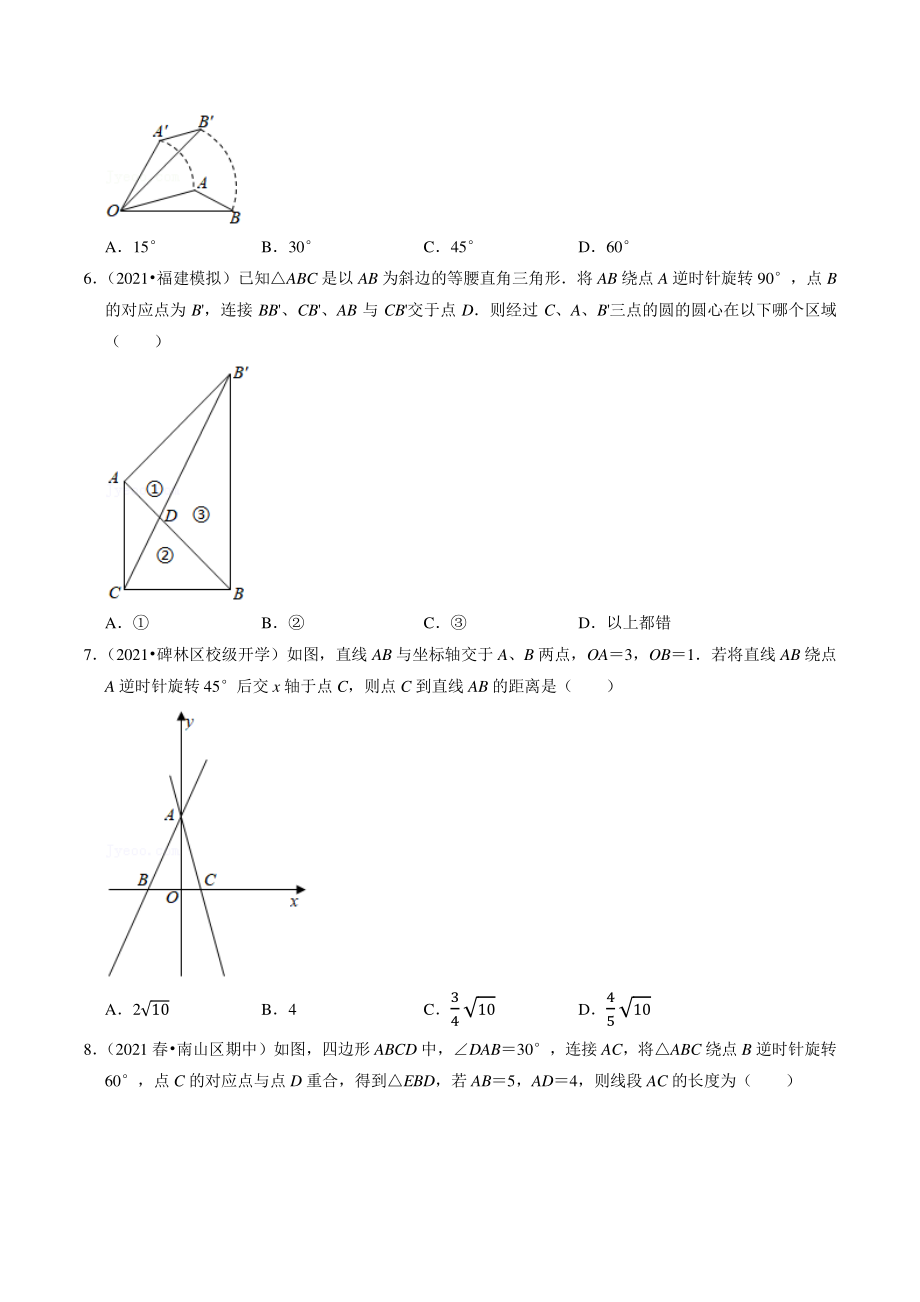
3、为斜边的等腰直角三角形将 AB 绕点 A 逆时针旋转 90，点 B 的对应点为 B，连接 BB、CB、AB 与 CB交于点 D则经过 C、A、B三点的圆的圆心在以下哪个区域 （ ） A B C D以上都错 7 （2021碑林区校级开学）如图，直线 AB 与坐标轴交于 A、B 两点，OA3，OB1若将直线 AB 绕点 A 逆时针旋转 45后交 x 轴于点 C，则点 C 到直线 AB 的距离是（ ） A210 B4 C3 4 10 D4 5 10 8 （2021 春南山区期中）如图，四边形 ABCD 中，DAB30，连接 AC，将ABC 绕点 B 逆时针旋转 60，点 C 的对应点与点 D 重合，
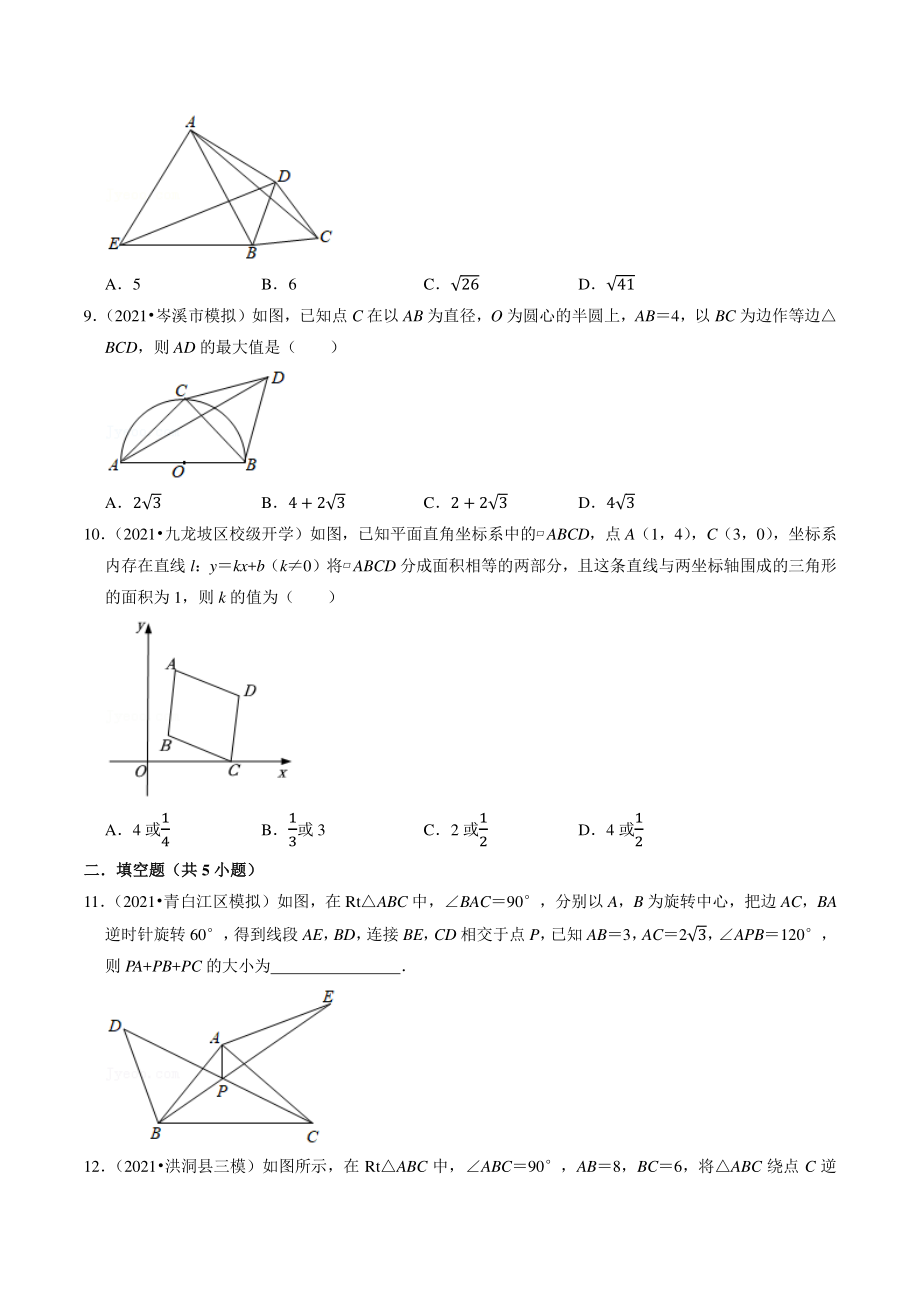
4、得到EBD，若 AB5，AD4，则线段 AC 的长度为（ ） A5 B6 C26 D41 9 （2021岑溪市模拟）如图，已知点 C 在以 AB 为直径，O 为圆心的半圆上，AB4，以 BC 为边作等边 BCD，则 AD 的最大值是（ ） A23 B4 + 23 C2 + 23 D43 10 （2021九龙坡区校级开学）如图，已知平面直角坐标系中的ABCD，点 A（1，4） ，C（3，0） ，坐标系 内存在直线 l：ykx+b（k0）将ABCD 分成面积相等的两部分，且这条直线与两坐标轴围成的三角形 的面积为 1，则 k 的值为（ ） A4 或1 4 B1 3或 3 C2 或1 2 D4 或1
5、 2 二填空题（共二填空题（共 5 小题）小题） 11 （2021青白江区模拟）如图，在 RtABC 中，BAC90，分别以 A，B 为旋转中心，把边 AC，BA 逆时针旋转 60， 得到线段 AE， BD， 连接 BE， CD 相交于点 P， 已知 AB3， AC23， APB120， 则 PA+PB+PC 的大小为 12 （2021洪洞县三模）如图所示，在 RtABC 中，ABC90，AB8，BC6，将ABC 绕点 C 逆 时针旋转 90得到ABC，连接 AA，BB，并延长 BB交 AA于点 D，则 BD 的长为 13 （2021宣州区校级开学）四边形 ABCD 是正方形，点 E 是对角线
6、 AC 上一点，EFDC，垂足为 F （1）如图，连接 BE、DE，若 EF4，BE5，求 AB （2） 如图， 将 RtCEF 绕点 C 顺时针旋转 45， 顶点 E 恰好落在 BC 上， 连接 AE， 取 AE 边中点 G， 连接 GF、DF，则 = 14 （2021沙坪坝区校级开学）如图 1，一副直角三角板ABC 和DEF，BACEDF90，B 45，F30，点 B、D、C、F 在同一直线上，点 A 在 DE 上如图 2，ABC 固定不动，将EDF 绕点 D 逆时针旋转 （0135）得EDF，当直线 EF与直线 AC、BC 所围成的三角形为 等腰三角形时， 的大小为 15 （2021芜湖
7、模拟）如图 1，含 30和 45角的两块直角三角板 ABC 和 DEF 叠合在一起，边 BC 与 EF 重合，BCEF12cm （1）阴影部分的周长为 cm（结果保留根号） ； （2）如图 2，点 P 为边 EF（BC）的中点，现将直角三角板 ABC 绕点 P 按逆时针方向旋转角度 ，设边 AB 与 EF 相 交 于 点 Q ， 则 在 0 90 的 变 化 过 程 中 ， 点 Q 移 动 的 路 径 长 度 为 cm（结果保留根号） 三解答题（共三解答题（共 5 小题）小题） 16 （2021太原二模）综合与实践 问题背景 数学小组在一次课外学习交流时，组内一同学提出如下问题：在ABC 中，
8、ACB90，D 为 BC 边 上一点， 但不与点 B， 点 C 重合， 过点 D 作 DEAB 于点 E 连接 AD， M 为 AD 的中点， 连接 EM， CM 观察发现 （1）如图 1，EM 与 CM 之间的数量关系是 ； 思考分享 （2）如图 2，将BDE 绕点 B 顺时针旋转，其他条件不变，则（1）中的结论还成立，请证明 小明是这样思考的：延长 DE 至点 D，使得 EDDE，连接 AD运用三角形中位线定理，按照他 的思路或采用其他方法证明； 探究计算 （3）若ABC30，AC4，DE2，在BDE 绕点 B 旋转一周的过程中，当直线 DE 经过点 A 时， 线段 AD 的长为 17 （
9、2021碑林区校级开学）在菱形 ABCD 中，BAD120，E 是对角线 BD 上的一点，连接 AE （1）当 E 在 AB 的中垂线上时，把射线 EA 绕点 E 顺时针旋转 90后交 CD 于 F，连接 BF如图， 若 AB4，求 EF 的长； （2）在（1）的条件下，连接 BF，把BEF 绕点 B 顺时针旋转得到BHK，如图，连接 CH，点 N 为 CH 的中点，连接 AN，求 AN 的最大值 18 （2021太原一模）综合与探究 问题情境 在 RtABC 中，BAC90，ABAC，点 D 是射线 BC 上一动点，连接 AD，将线段 AD 绕点 A 逆时 针旋转 90至 AE，连接 DE，
10、CE 探究发现： （1）如图 1，BDCE，BDCE，请证明； 探究猜想 （2）如图 2，当 BD2DC 时，猜想 AD 与 BC 之间的数量关系，并说明理由； 探究拓广 （3）当点 D 在 BC 的延长线上时，探究并直接写出线段 BD，DC，AD 之间的数量关系 19 （2021碑林区校级开学）如图 1，在ABC 中，A120，ABAC，点 D、E 分别在边 AB、AC 上， ADAE，连接 BE，点 M、N、P 分别为 DE、BE、BC 的中点，连接 NM、NP （1）图 1 中，线段 NM、NP 的数量关系是 ，MNP 的度数为 ； （2）将ADE 绕点 A 顺时针旋转到如图 2 所示的
11、位置，连接 MP，你认为NMP 是什么特殊三角形， 请写出你的猜想并证明你的结论； （3）把ADE 绕点 A 在平面内旋转，若 AD3，AB5，请写出MNP 面积的最大值 20 （2021沙坪坝区校级开学）如图，ABC 和MBN 均为等腰直角三角形，ABCMBN90，AB BC，MBNB现将MBN 绕点 B 旋转 （1）如图 1，若 A、M、N 三点共线，AM= 10，求点 C 到直线 BN 的距离； （2）如图 2，连接 AN、CM，点 H 为线段 CM 的中点，连接 BH求证：ANBH； （3）如图 3，若点 P 在线段 AC 上，且 AB82，AP14，在ABP 内部有一点 O，请直接写
12、出 1 2OB+OA+ 5 2 OP 的最小值 2022 年中考数学复习新题速递之图形的旋转（年中考数学复习新题速递之图形的旋转（中考新题汇编中考新题汇编） 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 10 小题）小题） 1 （2021垦利区一模）随着人们健康生活理念的提高，环保意识也不断增强，以下是回收、绿色包装、节 水、低碳四个标志，其中是中心对称图形的是（ ） A B C D 【解答】解：选项 A、C、D 不能找到这样的一个点，使这些图形绕某一点旋转 180后与原来的图形重 合，所以它们不是中心对称图形； 选项 B 能找到这样的一个点，使这个图形绕某一点旋转 180后
13、与原来的图形重合，所以它是中心对称 图形； 故选：B 2 （2021河北模拟）如图是由边长均相等的两个正方形和六个等边三角形组成的图案，现有两个正方形和 一个等边三角形被涂黑，若再有 n 个等边三角形被涂黑，使所有涂黑的新图案既是中心对称图形又是轴 对称图形，则 n 的值是（ ） A4 或 5 B3 或 5 C2 或 3 D1 或 3 【解答】解：如图所示，再涂黑 1、2、3 号正三角形，或涂黑 1、2、3、4、5 号正三角形都可使它们和 原来涂黑的小正三角形组成新的图案后既是轴对称图形，又是中心对称图形， 故选：B 3 （2021通城县模拟）在平面直角坐标系中，将点 P（1，2）向右平移 3
14、 个单位长度得到点 P1，则点 P1关于原点的对称点 P2的坐标为（ ） A （2，2） B （2，2） C （2，2） D （3，2） 【解答】解：将点 P（1，2）向右平移 3 个单位长度得到点 P1， 点 P1的坐标为： （2，2） ， 点 P1关于原点的对称点 P2的坐标为（2，2） 故选：B 4（2021春聊城期末） 如图， 在ABC中， BAC138， 将ABC绕点A按逆时针方向旋转得到ABC 若 点 B刚好落在 BC 边上，且 ABCB，则C 的度数为（ ） A13 B14 C15 D16 【解答】解：ABCB， CCAB， ABBC+CAB2C， 将ABC 绕点 A 按逆时针方
15、向旋转得到ABC， CC，ABAB， BABB2C， B+C+CAB180， 3C180138， C14， 故选：B 5 （2021 春万山区期末）如图所示，将AOB 绕点 O 按逆时针方向旋转 45后得到AOB，若AOB 15，那么AOB的度数是（ ） A15 B30 C45 D60 【解答】解：将AOB 绕点 O 按逆时针方向旋转 45后得到AOB， AOA45，AOBAOB15， AOBAOAAOB451530， 故选：B 6 （2021福建模拟）已知ABC 是以 AB 为斜边的等腰直角三角形将 AB 绕点 A 逆时针旋转 90，点 B 的对应点为 B，连接 BB、CB、AB 与 CB交
16、于点 D则经过 C、A、B三点的圆的圆心在以下哪个区域 （ ） A B C D以上都错 【解答】解：如图，分别画出 AC，AB的垂直平分线，交点为 O， 根据垂直平分线上的点到线段两端的距离相等， OAOCOB， 则点 O 即为经过 C、A、B三点的圆的圆心， 故选：D 7 （2021碑林区校级开学）如图，直线 AB 与坐标轴交于 A、B 两点，OA3，OB1若将直线 AB 绕点 A 逆时针旋转 45后交 x 轴于点 C，则点 C 到直线 AB 的距离是（ ） A210 B4 C3 4 10 D4 5 10 【解答】解：过点 B 作 BDAB，交 AC 于点 D，过点 D 作 DEx 轴于 E
17、， BAC45，故ABD 为等腰直角三角形，则 ABBD， ABC+BAO90，ABC+DBE90， BAODBE， 在AOB 与BED 中， = = = 90 = ， AOBBED（AAS） ， OABE3，OBDE1， OE312， 点 D 的坐标为（2，1） ， 设直线 AC 的表达式为 ykx+3， 把点 D 的坐标代入得 2k+31，解得 k2， 直线 AC 的表达式为 y2x+3， 令 y0，则2x+30，解得 x= 3 2， C（3 2，0） ， BC= 5 2， AB= 2+ 2= 32+ 12= 10， 设 C 点到直线 AB 的距离为 h， 1 2ABh= 1 2BCOA，
18、 h= = 5 23 10 = 310 4 ， 故选：C 8 （2021 春南山区期中）如图，四边形 ABCD 中，DAB30，连接 AC，将ABC 绕点 B 逆时针旋转 60，点 C 的对应点与点 D 重合，得到EBD，若 AB5，AD4，则线段 AC 的长度为（ ） A5 B6 C26 D41 【解答】解：EBD 是由ABC 旋转得到， EBDABC， BABE，ABE60，ACDE， ABE 是等边三角形， EAB60， BAD30， EAD90， AEAB5，AD4， DE= 2+ 2= 52+ 42= 41， ACDE= 41， 故选：D 9 （2021岑溪市模拟）如图，已知点 C
19、在以 AB 为直径，O 为圆心的半圆上，AB4，以 BC 为边作等边 BCD，则 AD 的最大值是（ ） A23 B4 + 23 C2 + 23 D43 【解答】解：如图，将ABD 绕点 B 逆时针旋转 60得CBE， ADCE，ABBE，ABE60， ABE 是等边三角形， 连接 EO 并延长交半圆于点 C，此时 EC 最大， O 为 AB 的中点， EOAB， 在 RtAOE 中，EO= 2 2= 42 22= 23， EC 的最大值为：EO+OC23 +2， AD 的最大值为 23 +2， 故选：C 10 （2021九龙坡区校级开学）如图，已知平面直角坐标系中的ABCD，点 A（1，4）
20、 ，C（3，0） ，坐标系 内存在直线 l：ykx+b（k0）将ABCD 分成面积相等的两部分，且这条直线与两坐标轴围成的三角形 的面积为 1，则 k 的值为（ ） A4 或1 4 B1 3或 3 C2 或1 2 D4 或1 2 【解答】解：直线 l：ykx+b（k0） ， 令 x0，yb，令 y0，x= ， 与两坐标轴围成的三角形的面积为 1， 所以1 2 |b| |1， 化简得，b22|k|， 因为点 A（1，4） ，C（3，0）的中点 O（2，2） ， 直线 l：ykx+b（k0）将ABCD 分成面积相等的两部分， 所以直线 l：ykx+b 过点 O（2，2） ， 所以 2k+b2， 所
21、以 b22k， b22|k|， （22k）22|k|， （22k）22k， 解得 k2 或 k= 1 2， 或（22k）22k， 解得此方程无解， 则 k 的值为 2 或1 2， 故选：C 二填空题（共二填空题（共 5 小题）小题） 11 （2021青白江区模拟）如图，在 RtABC 中，BAC90，分别以 A，B 为旋转中心，把边 AC，BA 逆时针旋转 60， 得到线段 AE， BD， 连接 BE， CD 相交于点 P， 已知 AB3， AC23， APB120， 则 PA+PB+PC 的大小为 39 【解答】解：连接 AD，CE， 以 A，B 为旋转中心，把边 AC，BA 逆时针旋转 6
22、0，得到线段 AE，BD， ADAB，ACAE，ABDCAE60， ABD 和ACE 为等边三角形， BADCAE60， DACBAE， 在ADC 和ABE 中， = = = ， ADCABE（SAS） ， AEBACD， 在 PE 上截取 PHPA，连接 HA，则PAH 为等边三角形， HAPA，PAH60， PACHAE， 在CPA 和EHA 中， = = = ， CPAEHA（AAS） ， PCEH， PB+PC+PAPB+EH+PHBE 过点 E 作 EGBA，交 BA 的延长线于点 G， BAC90，CAE60， EAG30， EG= 1 2AE= 3， AG3， BG6， BE=
23、2+ 2= 39 PA+PB+PC= 39 故答案为39 12 （2021洪洞县三模）如图所示，在 RtABC 中，ABC90，AB8，BC6，将ABC 绕点 C 逆 时针旋转 90得到ABC，连接 AA，BB，并延长 BB交 AA于点 D，则 BD 的长为 2 【解答】解：如图，由ABC90，以 B 为坐标原点，建立平面直角坐标系， AB8，BC6， A（0，8）B（0，0） ，C（6，0） ， 由旋转可知：ABAB8，BCBC6，ABCABC90， A（14，6） ，B（6，6） ， 设直线 AA的解析式为：yk1x+b1， 1 = 8 141+ 1= 6， 解得1 = 1 7 1= 8
24、， 直线 AA的解析式为：y= 1 7x+8； 设直线 BB的解析式为：yk2x， 6k26， 解得 k21， 直线 BB的解析式为：yx， = 1 7 + 8 = ， 解得 = 7 = 7 ， D（7，7） ， BD= 72+ 72=72，BB= 62+ 62=62， BDBDBB= 2 故答案为：2 13 （2021宣州区校级开学）四边形 ABCD 是正方形，点 E 是对角线 AC 上一点，EFDC，垂足为 F （1）如图，连接 BE、DE，若 EF4，BE5，求 AB 7 （2） 如图， 将 RtCEF 绕点 C 顺时针旋转 45， 顶点 E 恰好落在 BC 上， 连接 AE， 取 AE
25、 边中点 G， 连接 GF、DF，则 = 2 【解答】解： （1）如图所示：过点 E 作 EGBC 于 E 四边形 ABCD 为正方形， AC 平分DCB EFDC，EGBC， EFGE 又EFCFCGEGC90， 四边形 EFCG 为正方形， CGEGEF4 在 RtBEG 中，依据勾股定理得：BG= 2 2= 52 42=3， ABBC4+37； （2）如图，连接 BG、BF， AC 是正方形 ABCD 的对角线， ABAD，DACBAC， AFAF， AFDAFB（SAS） ， DFBF， 四边形 ABCD 是正方形， ABC90， 将 RtCEF 绕点 C 顺时针旋转 45， AFE9
26、0， ABCAFE90， 点 G 是 AE 中点， AGFG，AGBG， GAFAFG，BAGABG， EGFGAF+AFG2GAF， BGEBAG+ABG2BAG， BGF2BAC， BAC45， BGF2BAC90， 在 RtABE 中，BG= 1 2AE， 在 RtAFE 中，FG= 1 2AE， BGFG， BGF90， BGF 为等腰直角三角形， BF= 2FG， DFBF， DF= 2FG， =2， 故答案为：2 14 （2021沙坪坝区校级开学）如图 1，一副直角三角板ABC 和DEF，BACEDF90，B 45，F30，点 B、D、C、F 在同一直线上，点 A 在 DE 上如图
27、 2，ABC 固定不动，将EDF 绕点 D 逆时针旋转 （0135）得EDF，当直线 EF与直线 AC、BC 所围成的三角形为 等腰三角形时， 的大小为 7.5或 75或 97.5或 120 【解答】解：设直线 EF与直线 AC、BC 分别交于点 P、Q， CPQ 为等腰三角形， PCQ 为顶角或CPQ 为顶角或CQP 为顶角， 当PCQ 为顶角时，CPQCQP，如图 1， BACEDF90，B45，F30， EDF90，ACB45，EFD30， CPQ+CQPACB45， CQP22.5， EFDCQP+FDQ， FDQEFDCQP3022.57.5， 7.5； 如图 2，CPQ 为等腰三角
28、形中，PCQ 为顶角， CPQCQP67.5， EDF90，F30， E60， EDQCQPE67.5607.5， EDE90+7.597.5； 当CPQ 为顶角时，CQPPCQ45， CPQ90，如图 3， DEFCQP+QDE， QDEDEFCQP604515， 901575； 如图 4，当CQP 为顶角时，CPQPCQ45， CQP90， QDF90DFE60， QDEEDFQDF30， EDEEDQ+QDE90+30120； 综上所述， 的大小为 7.5或 75或 97.5或 120 故答案为：7.5或 75或 97.5或 120 15 （2021芜湖模拟）如图 1，含 30和 45角
29、的两块直角三角板 ABC 和 DEF 叠合在一起，边 BC 与 EF 重合，BCEF12cm （1）阴影部分的周长为 （6 + 63 + 122） cm（结果保留根号） ； （2）如图 2，点 P 为边 EF（BC）的中点，现将直角三角板 ABC 绕点 P 按逆时针方向旋转角度 ，设边 AB 与 EF 相交于点 Q，则在 090的变化过程中，点 Q 移动的路径长度为 23 cm（结果保 留根号） 【解答】解： （1）在 RtABC 中，ABC30，BC12cm， AC6cm，ABtan60AC63（cm） ， 在 RtDEF 中，DEF45，EF12cm， DEDFsin45EF= 2 2 1
30、262（cm） ， 阴影部分的周长为：BD+AB+DF+AC62 +63 +62 +66+63 +122（cm） ； 故答案为： （6+63 +122） ； （2）当 060时，点 Q 从 E 开始向 F 运动，且当 60时，此时 ABEF， 在 RtBQP 中，B30，BP6cm， PQ= 1 2BP3cm， EQ3cm， 当 6090时，点 Q 向点 E 作回头运动，当 90时，点 Q 停止运动， 在 RtBQP 中，B30，BP6cm， PQtan30BP23（cm） ， EQEPPQ623（cm） ， 点 Q 返回运动的路径长为 3（623）23 3（cm） ， 点 Q 的运动路径为
31、3+23 323（cm） ， 故答案为：23 三解答题（共三解答题（共 5 小题）小题） 16 （2021太原二模）综合与实践 问题背景 数学小组在一次课外学习交流时，组内一同学提出如下问题：在ABC 中，ACB90，D 为 BC 边 上一点， 但不与点 B， 点 C 重合， 过点 D 作 DEAB 于点 E 连接 AD， M 为 AD 的中点， 连接 EM， CM 观察发现 （1）如图 1，EM 与 CM 之间的数量关系是 EMCM ； 思考分享 （2）如图 2，将BDE 绕点 B 顺时针旋转，其他条件不变，则（1）中的结论还成立，请证明 小明是这样思考的：延长 DE 至点 D，使得 EDD
32、E，连接 AD运用三角形中位线定理，按照他 的思路或采用其他方法证明； 探究计算 （3）若ABC30，AC4，DE2，在BDE 绕点 B 旋转一周的过程中，当直线 DE 经过点 A 时， 线段 AD 的长为 2132 或 213 +2 【解答】解： （1）在ABC 中，ACB90，M 为 AD 的中点， CMMD， DEAB， AED 是直角三角形， EMMD， CMEM， 故答案为 CMEM； （2）成立，理由如下： 如图 1，延长 DE 到点 D，使得 DEDE，延长 AC 到点 A，使得 ACAC，分别连接 DA，DB，AB、 AD， DEBE， BE 为 DD的垂直平分线， BDBD，
33、 DBD2DBE， 同理可得，BABA，ABA2ABC， DBEABC， DBDABA DBD+ABDABA+ABD， DBADBA， 在DBA 和DBA 中， = = = ， DBADBA（SAS） ， DADA， DEDE，AMDM，ACAC， ME、MC 分别是DDA 和ADA的中位线， EM= 1 2DA，CM= 1 2DA， EMCM； （3）如图 2，当旋转角小于 180时， ABC30，AC4，ED2， AB8，BC43，BD4，BE23， BEED， ABE 是直角三角形， AE2AB2BE2，即 AE2641252， AE213， AD213 +2； 如图 3，当旋转角大于
34、180时， BEED， ABE 为直角三角形， AE2AB2BE2，即 AE2641252， AE213， AD213 2； 综上所述，AD 的长为 213 2 或 213 +2， 故答案为 213 2 或 213 +2 17 （2021碑林区校级开学）在菱形 ABCD 中，BAD120，E 是对角线 BD 上的一点，连接 AE （1）当 E 在 AB 的中垂线上时，把射线 EA 绕点 E 顺时针旋转 90后交 CD 于 F，连接 BF如图， 若 AB4，求 EF 的长； （2）在（1）的条件下，连接 BF，把BEF 绕点 B 顺时针旋转得到BHK，如图，连接 CH，点 N 为 CH 的中点，
35、连接 AN，求 AN 的最大值 【解答】解： （1）如图，连接 AC 交 BD 于 O， 菱形 ABCD 中，BAD120，AB4， AOB90，OBOD，ADBCAB4，BAODAO60， ABOADB30， 在 RtABO 中，OBABsinBAO4sin6023， BD2OB43， E 在 AB 的中垂线上， EAEB， BAEABO30， DAEBADBAE90， DE= = 4 30 = 83 3 ， 射线 EA 绕点 E 顺时针旋转 90后交 CD 于 F， AED+DEF90， AED90ADE60， DEF30， DBCABD30， DEFDBC， EFBC， = ，即 4 =
36、 83 3 43 ， EF= 8 3； （2）如图，过点 A 作 AGBC 于 G，连接 AC，GN， 四边形 ABCD 是菱形，BAD120， ABC60，ABBC， ABC 是等边三角形， AGBC， BGCG2， AG= 2 2= 42 22=23， 由旋转得：BHBEBDDE43 83 3 = 43 3 ， 点 G，N 分别是 BC，CH 的中点， GN= 1 2BH= 1 2 43 3 = 23 3 ， ANAG+GN23 + 23 3 = 83 3 ； AN 的最大值为83 3 18 （2021太原一模）综合与探究 问题情境 在 RtABC 中，BAC90，ABAC，点 D 是射线
37、 BC 上一动点，连接 AD，将线段 AD 绕点 A 逆时 针旋转 90至 AE，连接 DE，CE 探究发现： （1）如图 1，BDCE，BDCE，请证明； 探究猜想 （2）如图 2，当 BD2DC 时，猜想 AD 与 BC 之间的数量关系，并说明理由； 探究拓广 （3）当点 D 在 BC 的延长线上时，探究并直接写出线段 BD，DC，AD 之间的数量关系 【解答】 （1）证明：在 RtABC 中，ABAC， BACB45， 由旋转知，ADAE，DAE90， BAC90， BACDAE， BADCAE， ABAC， BADCAE（SAS） ， BDCE，BACE45， BCEACB+ACE90
38、， BCE90， BDCE； （2） = 10 6 ，理由： 设 DCx， BD2DC， DC2x， BCBD+DC3x， x= 1 3BC， 由（1）知，CEBD2x，BCE90， 在 RtDCE 中，根据勾股定理得，DE= 2+ 2= 2+ (2)2= 5x 在 RtADE 中，ADAE， AD= 2 2 DE= 10 2 x= 10 2 1 3BC= 10 6 BC， = 10 6 ； （3）2AD2DC2+BD2.理由：如备用图， 在 RtABC 中，ABAC， BACB45， 由旋转知，ADAE，DAE90， BAC90， BACDAE， BADCAE， ABAC， BADCAE（S
39、AS） ， BDCE，BACE45， BCEACB+ACE90， BCE90， DCE90，根据勾股定理得，DE2DC2+CE2， DE2DC2+BD2， 在 RtADE 中，ADAE， DE22AD2， 2AD2DC2+BD2 19 （2021碑林区校级开学）如图 1，在ABC 中，A120，ABAC，点 D、E 分别在边 AB、AC 上， ADAE，连接 BE，点 M、N、P 分别为 DE、BE、BC 的中点，连接 NM、NP （1）图 1 中，线段 NM、NP 的数量关系是 MNNP ，MNP 的度数为 60 ； （2）将ADE 绕点 A 顺时针旋转到如图 2 所示的位置，连接 MP，你
40、认为NMP 是什么特殊三角形， 请写出你的猜想并证明你的结论； （3）把ADE 绕点 A 在平面内旋转，若 AD3，AB5，请写出MNP 面积的最大值 【解答】解： （1）ABAC，ADAE， BDCE， 点 M、N、P 分别为 DE、BE、BC 的中点， MN= 1 2 ，PN= 1 2CE，MNAB，PNAC， MNPN，ENMEBA，ENPAEB， MNE+ENPABE+AEB， ABE+AEB180BAE60， MNP60， 故答案为：MNNP，MNP60 （2）MNP 是等边三角形，理由如下： 由旋转得：BADCAE， 又ABAC，ADAE， ABDACE（SAS） ， BDCE，A
41、BDACE， 点 M、N、P 分别为 DE、BE、BC 的中点， MN= 1 2 ，PN= 1 2CE，MNBD，PNCE， MNPN，ENMEBD，BPNBCE， ENPNBP+NPBNBP+ECB， EBDABD+ABEACE+ABE， MNPMNE+ENPACE+ABE+EBC+EBCECB180BAC60， MNP 是等边三角形； （3）由三角形三边关系可知：BDAB+AD， 即 BD8， BD 的最大值为 8， 由（2）知：MNP 是等边三角形，MN= 1 2BD， MN4 时，SMNP最大， SMNP最大为： 3 4 4 4 =43 20 （2021沙坪坝区校级开学）如图，ABC
42、和MBN 均为等腰直角三角形，ABCMBN90，AB BC，MBNB现将MBN 绕点 B 旋转 （1）如图 1，若 A、M、N 三点共线，AM= 10，求点 C 到直线 BN 的距离； （2）如图 2，连接 AN、CM，点 H 为线段 CM 的中点，连接 BH求证：ANBH； （3）如图 3，若点 P 在线段 AC 上，且 AB82，AP14，在ABP 内部有一点 O，请直接写出 1 2OB+OA+ 5 2 OP 的最小值 【解答】解： （1）如图 1，设 AN 交 BC 于点 K，作 CFBN，交 BN 的延长线于点 F，则F90， 由旋转得，CNAM= 10，BCNBAM， ABC90，C
43、KNAKB， BCN+CKNBAM+AKB90， ANC90； MBNB，MBN90， BNMBMN45， FNCFCN45， CFNF， CF2+NF2CN2， 2CF2（10）2， CF= 5， 点 C 到直线 BN 的距离是5 （2）证明：如图 2，设 AN 交 BH 于点 I，延长 BH 到点 D，使 DHBH，连接 DC， CHMH，CHDMHB， CHDMHB（SAS） ， CDMBNB，DHBM， CDBM， BCD+CBM180， ABN+CBMMBN+ABM+CBMMBN+ABC180， BCDABN， BCAB， BCDABN（SAS） ， CBDBAN， BAN+ABDC
44、BD+ABDABC90， AIB90， ANBH （3）如图 3，在直线 BC 下方作 PQOP，PGAP，使 PQ2PO，PG2PA，连接 OQ、QG、BG， OPQAPG90， QPGOPA90APQ， = =2， PQGPOA， = =2， QG2OA； OQ= 2+ 2= 2+ (2)2= 5PO， 1 2OB+OA+ 5 2 OP= 1 2（OB+2OA+5OP）= 1 2（OB+QG+OQ） ， OB+QG+OQBG， 当 OB+QG+OQBG 时，OB+QG+OQ 的值最小，此时1 2OB+OA+ 5 2 OP 的值最小； 则点 O、点 Q 落在 BG 上，如图 4，设 BG 交
45、 AC 于点 L，作 BRAC 于点 R， AC2AB2+BC22AB2，AB82， AC22（82）2， AC16， ARCR= 1 2AC8， BR= 1 2AC8， AP14， PR1486，GP2AP21428， GPBR， GPLBRL， = = 28 8 = 7 2， RL= 2 9PR= 2 9 6= 4 3，PL= 7 9PR= 7 9 6= 14 3 ， BRLGPL90， BL= 2+ 2=82+ (4 3) 2 = 437 3 ，GL= 2+ 2=282+ (14 3 )2= 1437 3 ， BGBL+GL= 437 3 + 1437 3 = 637， OB+QG+OQ 的最小值为637， 此时，1 2OB+OA+ 5 2 OP= 1 2（OB+QG+OQ）= 1 2 637 = 337， 1 2OB+OA+ 5 2 OP 的最小值为337
