1、 2022 年中考数学复习新题：年中考数学复习新题：图形的相似图形的相似 一选择题（共一选择题（共 10 小题）小题） 1 （2021安徽模拟）如图，在ABC 中，B60，C45，AB4，E 为 AC 中点，D 为 AB 上一 点，连接 DE，当AED60时，AD 的长为（ ） A23 B6 C3 D15 4 2 （2021福建模拟） 在平面直角坐标系中， 已知抛物线 y1mx2， y2nx2， 直线 yp， 且 mn0， p0 该 直线与两条抛物线的交点的横坐标从左到右分别为 n1、m1、m2、n2下列说法中正确的是（ ） 这两条抛物线为关于原点的位似图形； m1+m2n1+n2； 当 m9
2、n 时，m2m1m1n1 A B C D 3 （2021蚌埠二模）如图，在ABC 中，点 D 是 AB 上一点，且ABCD，SADC：SBDC5：4，CD 4，则 AC 长为（ ） A5 B6 C9 D8 5 5 4 （2021沙坪坝区校级开学）平行四边形 ABCD 如图所示，E 为 AB 上的一点，F、G 分别为 AC 与 DE、 DB 的交点若 AB：AE3：2，则四边形 BGFE 与ABCD 的面积之比为（ ） A7：60 B8：70 C5：43 D3：26 5 （2021安徽模拟）如图，在ABC 中，ACB90，D 点在 BC 边上， = 2 5，P 为 AB 边上一点， 当 PCPD
3、 时， 的值为（ ） A5 9 B5 8 C4 7 D3 5 6 （2021安徽模拟）在ABC 中，ABAC，D 为边 AB 上任意一点，下列命题为真命题的是（ ） A若 ADCDBC，则A36 B若A36，则 = 5;1 2 C若 = 5;1 2 ，且 D 为 AB 的黄金分割点，则 CD 平分ACB D若 CD 平分ACB，则 AD2ABBD 7 （2021 春济宁期末）线段 AB8，P 是 AB 的黄金分割点，且 APBP，则 BP 的长度为（ ） A45 4 B85 +8 C85 8 D45 +4 8 （2021禹城市模拟）在平面直角坐标系中，正方形 ABCD 的位置如图所示，点 A
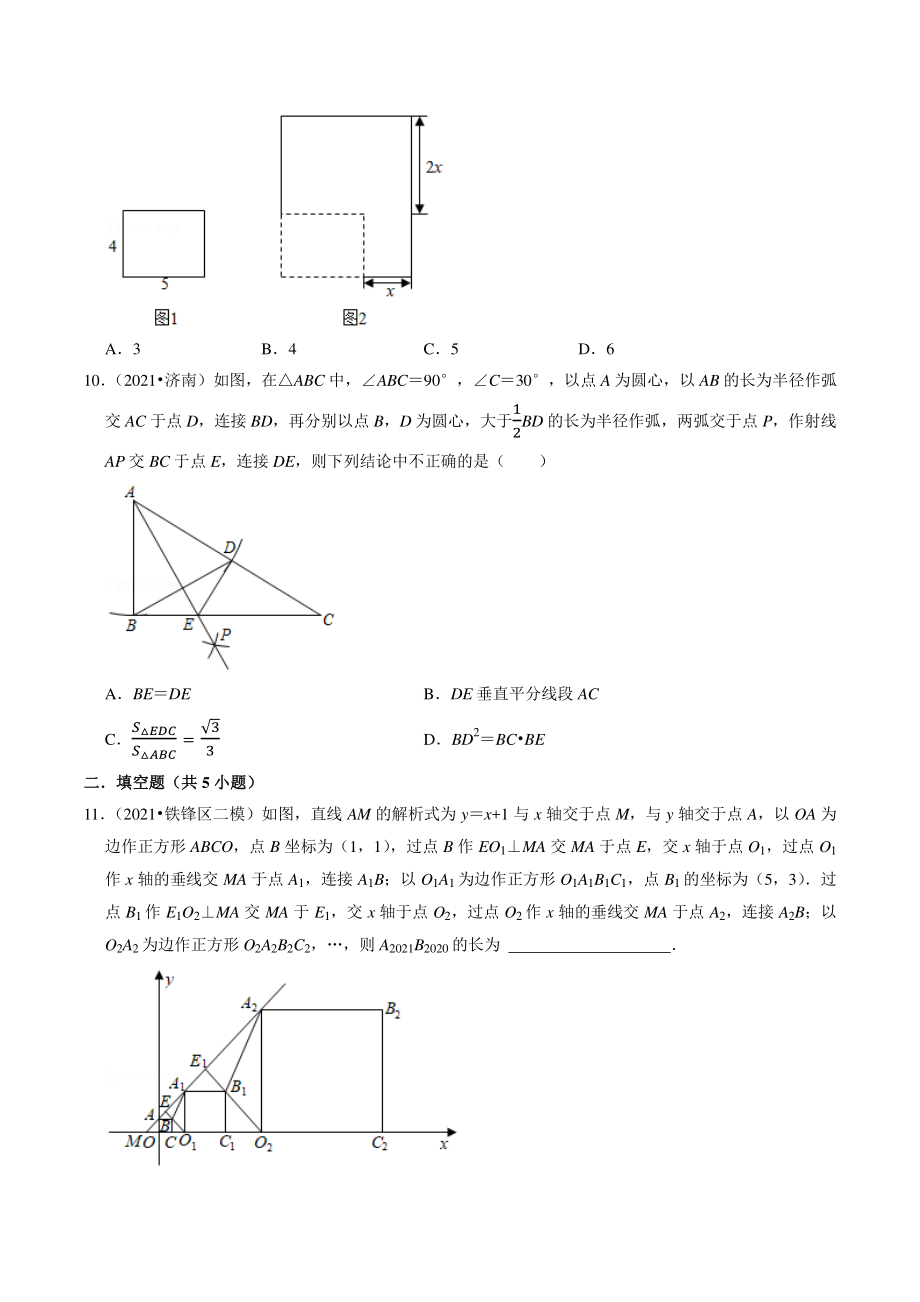
4、的坐标为（1，0） ，点 D 的坐标为（0，2） ，延长 CB 交 x 轴于点 A1，作正方形 A1B1C1C；延长 C1B1交 x 轴于点 A2，作正方形 A2B2C2C1按这样的规律进行下去，正方形 A2021B2021C2021C2020的面积为（ ） A5 (3 2) 2021 B5 (9 4) 2020 C5 (9 4) 4040 D5 (3 2) 4042 9 （2021河北模拟）如图 2 中的矩形边长分别是将图 1 中的矩形边长 4 拉长 2x，边长 5 拉长 x 得到的，若 两个矩形相似（不全等） ，则 x 的值是（ ） A3 B4 C5 D6 10 （2021济南）如图，在A
5、BC 中，ABC90，C30，以点 A 为圆心，以 AB 的长为半径作弧 交 AC 于点 D，连接 BD，再分别以点 B，D 为圆心，大于1 2BD 的长为半径作弧，两弧交于点 P，作射线 AP 交 BC 于点 E，连接 DE，则下列结论中不正确的是（ ） ABEDE BDE 垂直平分线段 AC C = 3 3 DBD2BCBE 二填空题（共二填空题（共 5 小题）小题） 11 （2021铁锋区二模）如图，直线 AM 的解析式为 yx+1 与 x 轴交于点 M，与 y 轴交于点 A，以 OA 为 边作正方形 ABCO，点 B 坐标为（1，1） ，过点 B 作 EO1MA 交 MA 于点 E，交
6、 x 轴于点 O1，过点 O1 作 x 轴的垂线交 MA 于点 A1，连接 A1B；以 O1A1为边作正方形 O1A1B1C1，点 B1的坐标为（5，3） 过 点 B1作 E1O2MA 交 MA 于 E1，交 x 轴于点 O2，过点 O2作 x 轴的垂线交 MA 于点 A2，连接 A2B；以 O2A2为边作正方形 O2A2B2C2，则 A2021B2020的长为 12 （2021诸城市二模）如图，在平面直角坐标系中，矩形 OABC 与反比例函数 y= （x0）的图象交于 D，E 两点，矩形顶点 A，C 在坐标轴上，OD：DE10：21，ODE90，若点 D 的坐标为（2，5） ， 则下列结论正
7、确的是 ASOEC10 BSDBE= 441 20 C = 21 4 D点 E 的坐标为（25 2 ，4 5） 13 （2021芜湖模拟）如图，在 RtABC 中，C90，AB10，BC6，点 D 是边 AC 上的动点，过 点 D 作 DEAB 于 E 点请探究下列问题： （1）若 DE4，则 CD ； （2）若 CD3，设点 F 是边 BC 上的动点，连接 FD、FE，以 FD、FE 为邻边作平行四边形 FDGE，且 使得顶点 G 恰好落在 AC 边上，则 CF 14 （2021禹城市模拟）如图，点 O 为正方形 ABCD 的中心，BE 平分DBC 交 DC 于点 E，延长 BC 到点 F，
8、使 FCEC，连接 DF 交 BE 的延长线于点 H，连接 OH 交 DC 于点 G，连接 HC则以下五个结论中 OH= 1 2BF； CHF45； BC （2+22） GH； DH 2HEHB； GFGD， 正确结论为 15 （2021潍坊一模）如图，AB 是O 的直径，D，E 是半圆上任意两点，连接 AD，DE，AE 与 BD 相交 于点 C，若添加一个条件使ADC 与ABD 相似，则可添加下列条件中的 A = BADDE CABDE DAD2BDCD 三解答题（共三解答题（共 5 小题）小题） 16 （2021安徽模拟）如图 1，RtABC 中，ABC90，AB2BC，D 为 AC 边上
9、一点，BEBD，BE 2BD，连接 DE 交 AB 于 F 点 （1）求证：CBDABE； （2）若DBC30，求 的值； （ 3 ） 如 图 2 ， 若 D 在 射 线 AC 上 ， 且 CD 1 ， 当 F 点 为 BE 中 点 时 ， 求 AB 的 值 17 （2021利辛县二模）如图 1，在正方形 ABCD 中，E 为 BC 延长线上一点，且 BC3CE，F 为 CD 的中 点，EF 的延长线交 AD 于点 G，连接 BG （1）求 的值； （2）求证：BGEG； （3）如图 2，M 为 AB 的中点，DM 交 BG 于点 N，连接 CN，求证：CNGE 18 （2021青白江区模拟）
10、如图 1，在ABC 中，BD 为ABC 的平分线，点 D 在 AC 上 （1）求证： = ； （2）如图 2，BAC90，已知 AE 为 BC 边的中线，且 AEBE在射线 BD 上取一点 A使 AEA E，AE 交 AC 于点 F，过点 A作 AB 的垂线，交 BA 的延长线于点 G，连接 EG 交 BD 于点 H，连接 CH 求证：四边形 AGAF 为矩形； 若 tanC= 3 4，BGH 的面积为 S，请求出CEH 的面积（用含 S 的代数式表示） 19 （2021安徽模拟）如图 1，在矩形 ABCD 中，BGAC 交 AC 于点 G，E 为 AB 的中点，EG 的延长线交 AD 于点
11、F，连接 CF （1）若 AFFD，求ABG 的大小 （2）如图 2，若EFC90，M 为 CD 的中点，连接 BF，FM 求证：BFFM 试求 2 2的值 20 （2021安徽模拟）如图 1，在正方形 ABCD 中，点 E 在直线 BC 上，CE= 1 2BC，过 B 作 BGDE 于 G， 交 DC 的延长线于 H （1）求证：BHDE； （2）连接 AG 交 DC 的延长线于 F，求证： = 3 2； （3）如图 2，若点 E 在 BC 的延长线上，连接 AG 交 DC 于 F 点，求 的值 2022 年中考数学复习新题速递之图形的相似（年中考数学复习新题速递之图形的相似（2021 年年
12、 9 月）月） 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 10 小题）小题） 1 （2021安徽模拟）如图，在ABC 中，B60，C45，AB4，E 为 AC 中点，D 为 AB 上一 点，连接 DE，当AED60时，AD 的长为（ ） A23 B6 C3 D15 4 【解答】解：如图，过点 A 作 AHBC 于 H， B60，AHBC， BAH30， BH= 1 2AB2，AH= 3BH23， sinC= ，C45， 2 2 = 23 ， AC26， 点 E 是 AC 的中点， AEEC= 6， AED60B，BACDAE， DAECAB， = ， 6 4 = 26，
13、AD3， 故选：C 2 （2021福建模拟） 在平面直角坐标系中， 已知抛物线 y1mx2， y2nx2， 直线 yp， 且 mn0， p0 该 直线与两条抛物线的交点的横坐标从左到右分别为 n1、m1、m2、n2下列说法中正确的是（ ） 这两条抛物线为关于原点的位似图形； m1+m2n1+n2； 当 m9n 时，m2m1m1n1 A B C D 【解答】解：mn0 可知这两条抛物线开口大小不同，即形状不同， 这两条抛物线不可能位似图形，故错误， y1mx2，y2nx2的对称轴均为直线 x0， 1:2 2 = 0，1:2 2 =0， m1+m2n1+n2，故正确， 当 m9n 时， 令 y1p
14、，则 mx29nx2p， 解得：x= 1 3 或 1 3 ， m1= 1 3 、m2= 1 3 ， m2m1= 2 3 ， 令 y2p，则 nx2p， 解得：x= 或 ， n1= ， m1n1= 2 3 ， m2m1m1n1，故正确 故选：C 3 （2021蚌埠二模）如图，在ABC 中，点 D 是 AB 上一点，且ABCD，SADC：SBDC5：4，CD 4，则 AC 长为（ ） A5 B6 C9 D8 5 5 【解答】解：SADC：SBDC5：4， SBCD：SABC4：9， ABCD，ABCCBD， ABCCBD， =（ ） 2=4 9， 4 = 2 3， AC6， 故选：B 4 （202
15、1沙坪坝区校级开学）平行四边形 ABCD 如图所示，E 为 AB 上的一点，F、G 分别为 AC 与 DE、 DB 的交点若 AB：AE3：2，则四边形 BGFE 与ABCD 的面积之比为（ ） A7：60 B8：70 C5：43 D3：26 【解答】解：AB：AE3：2， BE：AB1：3， SDBE= 1 3SABD= 1 6SABCD， 四边形 ABCD 是平行四边形， ABCD，AGGC， AEFCDF， = = 2 3， 设 AF2a，CF3a， AC5a， AGCG= 5 2a， FG= 1 2a， AG5FG， SDFG= 1 5SADG= 1 20SABCD， S四边形BGFE
16、SDBESDFG= 7 60SABCD， 四边形 BGFE 与ABCD 的面积之比为 7：60， 故选：A 5 （2021安徽模拟）如图，在ABC 中，ACB90，D 点在 BC 边上， = 2 5，P 为 AB 边上一点， 当 PCPD 时， 的值为（ ） A5 9 B5 8 C4 7 D3 5 【解答】解：过 P 作 PEAC 于 E，PFBC 于 F， 四边形 PECF 为矩形，PECF， PFBC， CFDF， APEABC， = = = 5 14， = ; = 5 14;5 = 5 9， 故选：A 6 （2021安徽模拟）在ABC 中，ABAC，D 为边 AB 上任意一点，下列命题为
17、真命题的是（ ） A若 ADCDBC，则A36 B若A36，则 = 5;1 2 C若 = 5;1 2 ，且 D 为 AB 的黄金分割点，则 CD 平分ACB D若 CD 平分ACB，则 AD2ABBD 【解答】解：A、ABAC，ADCDBC， AACD，BACBCDB， 设Ax，则ACDAx， BACBCDBA+ACD2x A+B+ACB180， x+2x+2x180， x36， A36正确，故本选项不符合题意 B、如图 1 中，作 CT 平分ACB，则ACTBCT36， BB，ABCT36， BCTBAC， = ， BC2BTBA， AACT36，BCTB72， ATTC，CBCT， ATC
18、TBC， 设 BCCTATx，ABy， 则有 x2（yx） y， x2+xyy20， x= 1+5 2 y 或;1;5 2 y（舍弃） ， = 5;1 2 ， 即 = 5;1 2 ，正确，本选项不符合题意 C、若 = 5;1 2 ，且 D 为 AB 的黄金分割点，点 D 有两个位置，这个结论错误本选项不符合题意 D、若 CD 平分ACB，AD2ABBD 不一定成立，错误，本选项不符合题意 故选：B 7 （2021 春济宁期末）线段 AB8，P 是 AB 的黄金分割点，且 APBP，则 BP 的长度为（ ） A45 4 B85 +8 C85 8 D45 +4 【解答】解：线段 AB8，P 是 A
19、B 的黄金分割点，且 APBP， BP= 51 2 AB= 51 2 845 4 故选：A 8 （2021禹城市模拟）在平面直角坐标系中，正方形 ABCD 的位置如图所示，点 A 的坐标为（1，0） ，点 D 的坐标为（0，2） ，延长 CB 交 x 轴于点 A1，作正方形 A1B1C1C；延长 C1B1交 x 轴于点 A2，作正方形 A2B2C2C1按这样的规律进行下去，正方形 A2021B2021C2021C2020的面积为（ ） A5 (3 2) 2021 B5 (9 4) 2020 C5 (9 4) 4040 D5 (3 2) 4042 【解答】解：正方形 ABCD 的点 A 的坐标为
20、（1，0） ，点 D 的坐标为（0，2） ， OA1，OD2，AD= 5， = 1 2， 延长 CB 交 x 轴与点 A1，作正方形 A1B1C1C， AA1BDAO， 1 = 1 2， ADAB= 5， A1B= 5 2 ， 第 1 个正方形的面积为：S1A1C25 （3 2） 2， 同理可得，A2c2（3 2 5 + 1 2 3 2 5）2， 第二个正方形面积为：S25 （3 2）4， . 第 n 个正方形面积为：Sn5 （3 2） 2n， 第 2021 个正方形的面积为：S20215 （3 2） 4042， 故选：D 9 （2021河北模拟）如图 2 中的矩形边长分别是将图 1 中的矩形
21、边长 4 拉长 2x，边长 5 拉长 x 得到的，若 两个矩形相似（不全等） ，则 x 的值是（ ） A3 B4 C5 D6 【解答】解：由题意，两个矩形相似， 4 5: = 5 4:2或 4 4:2 = 5 5:， 解得 x3 或 0（0 不符合题意舍弃） ， 故选：A 10 （2021济南）如图，在ABC 中，ABC90，C30，以点 A 为圆心，以 AB 的长为半径作弧 交 AC 于点 D，连接 BD，再分别以点 B，D 为圆心，大于1 2BD 的长为半径作弧，两弧交于点 P，作射线 AP 交 BC 于点 E，连接 DE，则下列结论中不正确的是（ ） ABEDE BDE 垂直平分线段 A
22、C C = 3 3 DBD2BCBE 【解答】解：由题意可得ABC90，C30，ABAD，AP 为 BD 的垂直平分线， BEDE， BAEDAE30， AEC 是等腰三角形， ABAD，AC2AB， 点 D 为 AC 的中点， DE 垂直平分线段 AC， 故选项 A，B 正确，不符合题意； 在ABC 和EDC 中，CC，ABCEDC90， ABCEDC， = = ， = 30 = 3 2 ，DC= 1 2 ， =3， = (3)2= 3， = 1 3，故选项 C 错误，符合题意； 在ABD 中，ABAD，BAD60， ABD 是等边三角形， ABDADB60， DBEBDE30， 在BED
23、和BDC 中，DBCEBD30，BDEC30， BEDBDC， = ， BD2BCBE，故选项 D 正确，不符合题意 故选：C 二填空题（共二填空题（共 5 小题）小题） 11 （2021铁锋区二模）如图，直线 AM 的解析式为 yx+1 与 x 轴交于点 M，与 y 轴交于点 A，以 OA 为 边作正方形 ABCO，点 B 坐标为（1，1） ，过点 B 作 EO1MA 交 MA 于点 E，交 x 轴于点 O1，过点 O1 作 x 轴的垂线交 MA 于点 A1，连接 A1B；以 O1A1为边作正方形 O1A1B1C1，点 B1的坐标为（5，3） 过 点 B1作 E1O2MA 交 MA 于 E1
24、，交 x 轴于点 O2，过点 O2作 x 轴的垂线交 MA 于点 A2，连接 A2B；以 O2A2为边作正方形 O2A2B2C2，则 A2021B2020的长为 320205 【解答】解：直线 AM 的解析式为 yx+1 与 x 轴交于点 M，与 y 轴交于点 A， 当 x0 时，y1， 当 y0 时，x1， 则 M 点坐标为（1，0） ，A 点坐标为（0，1） ，即 OMOA1， AMO45， EO1MA， MEO1是等腰直角三角形，BCO1是等腰直角三角形， MO11+1+13， EO1EA1= 32 2 ，BO1= 2，EB= 2 2 ， A1B= 1 2 + 2= 5， 点 B1的坐标
25、为（5，3） ，可知第二个正方形的边长是 3，MO29， 同理 E1O2E1A2= 92 2 ，B1O232，E1B1= 32 2 ， A2B135， 同理第三个正方形的边长是 9，MO227，E2O3E2A3= 272 2 ，B2O392，E2B2= 92 2 ，A3B295， . 依次类推，An+1Bn= 35， 故答案为：320205 12 （2021诸城市二模）如图，在平面直角坐标系中，矩形 OABC 与反比例函数 y= （x0）的图象交于 D，E 两点，矩形顶点 A，C 在坐标轴上，OD：DE10：21，ODE90，若点 D 的坐标为（2，5） ， 则下列结论正确的是 BCD ASO
26、EC10 BSDBE= 441 20 C = 21 4 D点 E 的坐标为（25 2 ，4 5） 【解答】解：四边形 OABC 为矩形，D（2，5） ， OA5，AD2，OD= 2+ 2= 29， 又OD：DE10：21， DE= 21 1029， ODE90， ODA+BDE90， 又ODA+AOD90， BDEAOD， OADDBE90， OADDBE， = = ，即 5 = 2 = 10 21， BD= 21 2 ，BE= 21 5 ， OCAD+BD2+ 21 2 = 25 2 ，ECBCBE5 21 5 = 4 5， SOEC= 1 2OCCE= 1 2 25 2 4 5 =5， 故
27、 A 错误； 不符合题意； SDEB= 1 2BDBE= 1 2 21 2 21 5 = 441 20 ， 故 B 正确， 符合题意； = 21 5 4 5 = 21 5 ， 故 C 正确， 符合题意； CO= 25 2 ，EC= 4 5，则点 E 的坐标为（ 25 2 ，4 5） ， 故 D 正确， 符合题意， 故正确答案为：BCD 13 （2021芜湖模拟）如图，在 RtABC 中，C90，AB10，BC6，点 D 是边 AC 上的动点，过 点 D 作 DEAB 于 E 点请探究下列问题： （1）若 DE4，则 CD 4 3 ； （2）若 CD3，设点 F 是边 BC 上的动点，连接 FD
28、、FE，以 FD、FE 为邻边作平行四边形 FDGE，且 使得顶点 G 恰好落在 AC 边上，则 CF 12 5 【解答】解： （1）C90，AB10，BC6， AC= 2 2=8， sinA= 3 5，cosA= 4 5，tanA= 3 4， DEAB， sinA= = 3 5，DE4， AD= 20 3 ， CDACAD= 4 3， 故答案为：4 3； （2）如图所示，四边形 FDGE 是平行四边形， EFDG， BEFA，EFBC90， CD3， AD5， cosA= = 4 5， AE4，BEABAE6， sinBEFsinA= 3 5， = 3 5， BF= 18 5 ，CFBCBF
29、= 12 5 ， 故答案为：12 5 14 （2021禹城市模拟）如图，点 O 为正方形 ABCD 的中心，BE 平分DBC 交 DC 于点 E，延长 BC 到点 F，使 FCEC，连接 DF 交 BE 的延长线于点 H，连接 OH 交 DC 于点 G，连接 HC则以下五个结论中 OH= 1 2BF；CHF45；BC（2+22）GH；DH 2HEHB；GFGD，正确结论为 【解答】解：在正方形 ABCD 中，BCEDCF，BCDC， ECCF，BCEDCF，BCDC， BCEDCF（SAS） ， CBECDF， CBE+BEC90，BECDEH， DEH+CDF90， BHDBHF90， BE
30、 平分DBC， HBDHBF， BHBH， BHDHBF（ASA） ， DHHF， ODOB， OH 是DBF 的中位线， OH= 1 2BF， 故正确； 四边形 ABCD 是正方形，BE 是DBC 的平分线， BCCD，BCDDCF，EBC22.5， CECF， RtBCERtDCF（SAS） ， EBCCDF22.5， BFH90CDF9022.567.5， OH 是DBF 的中位线，CDAF， OH 是 CD 的垂直平分线， DHCH， CDFDCH22.5， HCF90DCH9022.567.5， CHF180HCFBFH18067.567.545， 故正确； OH 是DBF 的中位线
31、， OHBF，OH= 1 2BF，OG= 1 2BC， OHBHBF， BE 是DBF 的平分线， DBHHBF， OHBHBO， OHBO， 设正方形的边长为 2a，则 BC2a，OGa，BD22a， OBOH= 2a， GHOHOG= 2aa（2 1）a， = 2 (2;1) =2+22， BC（2+2）GH， 故成立； DBF45，BE 是DBF 的平分线， DBH22.5， 由知HBCCDF22.5， DBHCDF， BHDBHD， DHEBHD， = ， DH2HEHB， 故成立； OH 是DBF 的中位线， G 是 DC 的中点， DGGC， 在 RtCGF 中 GFGC，即 GF
32、DG， 故不成立， 故答案为： 15 （2021潍坊一模）如图，AB 是O 的直径，D，E 是半圆上任意两点，连接 AD，DE，AE 与 BD 相交 于点 C，若添加一个条件使ADC 与ABD 相似，则可添加下列条件中的 B，D A = BADDE CABDE DAD2BDCD 【解答】解：在ADC 和ADB 中，当 ADDE 时，ADCBDA， ADCBDC， ADCBDA， 另外当 AD2BDCD 时，则有 = ， ADCADB， ADCBDA， 故答案为：B，D 三解答题（共三解答题（共 5 小题）小题） 16 （2021安徽模拟）如图 1，RtABC 中，ABC90，AB2BC，D 为
33、 AC 边上一点，BEBD，BE 2BD，连接 DE 交 AB 于 F 点 （1）求证：CBDABE； （2）若DBC30，求 的值； （3）如图 2，若 D 在射线 AC 上，且 CD1，当 F 点为 BE 中点时，求 AB 的值 【解答】解： （1）BEBD， DBE90ABC， CBDABE， AB2BC，BE2BD， = 2 = ， CBDABE； （2）如图 1，过点 D 作 DHBC 于 H， ABC90，AB2BC， AC= 2+ 2 = 5BC， CBDABE， = = 1 2，AEBBDC， AE2CD， DHBC， ABCDHC90， 又CC， ABCDHC， = = ，
34、CH= 5 5 CD，DH= 25 5 CD， DBC30， BD2DH= 45 5 CD， AEBBDC，BDC+ADB180， AEB+ADB180， 点 A，点 E，点 B，点 D 四点共圆， AEDABD，BAEBDE， AEFDBF， = ， = 5 2 ； （3）如图 2，过点 A 作 ANBE 于 N， F 点为 BE 中点，BE2BD， BFEF= 1 2BEBD， 又EBD90， BFDBDF45， CBDABE， AE2CD2，AEBADB45， 又BFDAFE45， AEFAFE， FAE90，AEAF2， EF22， ANBE， ANENFN= 2， EFBF22， B
35、N32， AB= 2+ 2 = 2 + 18 =25 17 （2021利辛县二模）如图 1，在正方形 ABCD 中，E 为 BC 延长线上一点，且 BC3CE，F 为 CD 的中 点，EF 的延长线交 AD 于点 G，连接 BG （1）求 的值； （2）求证：BGEG； （3）如图 2，M 为 AB 的中点，DM 交 BG 于点 N，连接 CN，求证：CNGE 【解答】解： （1）F 为 CD 的中点， DFCF， 四边形 ABCD 为正方形， ADBC， GDFECF90 又DFGCFE GDFECF（ASA） ， DGCE BC3CE， CE= 1 3BCDG， AGADDGBCCEBC
36、1 3BC= 2 3BC， = 2 3 1 3 =2； （2）过点 G 作 GHBC 于 H， CHDGCE= 1 3BC， EHCH+CE= 2 3BC， 在ABG 和HGE 中， = = 2 3 = = 90 = ， ABGHGE（SAS） ， BGEG； （3）过点 M 作 MTAD 交 BG 于 T， M 为 AB 的中点， MT= 1 2AGDG， ADMT， NMTNDG， 在MNT 和DNG 中， = = = ， MNTDNG（AAS） ， NTNG， BG4NG， = 3 4， BC3CE， = 3 4， = ， CBNEBG， CBNEBG， BCNBEG， CNEG 18
37、（2021青白江区模拟）如图 1，在ABC 中，BD 为ABC 的平分线，点 D 在 AC 上 （1）求证： = ； （2）如图 2，BAC90，已知 AE 为 BC 边的中线，且 AEBE在射线 BD 上取一点 A使 AEA E，AE 交 AC 于点 F，过点 A作 AB 的垂线，交 BA 的延长线于点 G，连接 EG 交 BD 于点 H，连接 CH 求证：四边形 AGAF 为矩形； 若tanC = 3 4 ， BGH的 面 积 为S ， 请 求 出 CEH的 面 积 （ 用 含S的 代 数 式 表 示） 【思路】 （1）过点 D 作 DMAB 交 BC 于点 M，证明ABCDMC，利用相似
38、三角形的性质可得对应 边成比例，利用角平分线的定义和平行线的性质，可推出BDMDBM，利用等角对等边，可证得 DMBM，由此可得结论； （2）利用等腰三角形的性质可得EBABAE，可证得 AGAC，再证明 AEAB，可证得四 边形 AGAF 为平行四边形；然后根据有一个角是直角的平行四边形是矩形，可证得结论； 在 RtABC 中，可设 AB3t，AC4t，可得到 BC5t，用含 t 的代数式表示出 EF，AG 的长，利用 （1 ）可得到 EH 和 GH 的比值；利用三角形的中线和面积公式可得到 SCEHSBEH，即可求出CEH 的面积 【解答】 （1）证明：过点 D 作 DMAB 交 BC 于
39、点 M， ABCDMC，ABDBDM， = ， = ， DMAB = ， BD 为ABC 的平分线， ABDDBM， BDMDBM， DMBM， = ； （2）解：证明：BAC90， ACAB， AGAB， AGAC， AEAE， BEAE， EBABAE， 又ABDDBE， ABDBAE， AEAB， 四边形 AGAF 为平行四边形， AGAB， 四边形 AGAF 为矩形； 解：由题意，在 RtABC 中，tanC= 3 4，设 AB3t，AC4t，则 BC5t， E 为 BC 边的中点，AEAB， EF 是ABC 的中线， EF= 3 2t，AEAE= 1 2BC= 5 2t， AGAF=
40、 5 2t 3 2tt， 在BEG 中由（1）可得： = = 5 3 3: = 5 8， AE 为 BC 边的中线， 5 8S CEHSBEH， = = = 5 8， SCEH= 5 8SBGH= 5 8S 19 （2021安徽模拟）如图 1，在矩形 ABCD 中，BGAC 交 AC 于点 G，E 为 AB 的中点，EG 的延长线交 AD 于点 F，连接 CF （1）若 AFFD，求ABG 的大小 （2）如图 2，若EFC90，M 为 CD 的中点，连接 BF，FM 求证：BFFM 试求 2 2的值 【思路】 （1）根据相似三角形的判定和性质得出EAFABC，进而利用三角函数解答即可； （2）
41、根据相似三角形的判定和性质得出AEFDFC，进而利用垂直的判定解答即可； 设 AEx，AFy，求出 AB2，AD2（用 a 表示） ，即可解决问题 【解答】证明： （1）F 是 AD 中点， AFFD， E 是 AB 中点， AEEB= 1 2AB， = 1 2， = = 1 2， EAFABC90， EAFABC， AEFBAC， AGEG， BGAC， EG= 1 2ABAEBE， AGAEBE= 1 2AB， = 1 2， sinABG= 1 2， ABG30； （2）EFC90， AFE+DFC90， AFEAEF90， DFCAEF， EAFD90， AEFDFC， = ， AE=
42、1 2AB，DC2DM， 1 2 = 2， = ， ABFDFM， AFMDMF， DMF+DFM90， AFB+DFM90， BFM90， BFFM； 设 AEx，AFy， 在 RtABG 中，AEBE， EAEG， EAGEGAFGC， 又EAFEFC90， FACFCA， FAFC， EAFEFCFDC90， EAFFDC， = ， = 22 ， 在 RtDFC 中，DF2+DC2FC2AF2， 4 4 2 + 42= 2， 2 2 = 2;1 2 ， 2 2 = 42 (:2 2 )2 = 42 2+42+44 2 = 4 2 21+4+ 4(21) 2 = 2 1 20 （2021安
43、徽模拟）如图 1，在正方形 ABCD 中，点 E 在直线 BC 上，CE= 1 2BC，过 B 作 BGDE 于 G， 交 DC 的延长线于 H （1）求证：BHDE； （2）连接 AG 交 DC 的延长线于 F，求证： = 3 2； （3）如图 2，若点 E 在 BC 的延长线上，连接 AG 交 DC 于 F 点，求 的值 【思路】 （1）证明DCEBCH（ASA） ，考点 BHDE （2）如图 1 中，设 BEECm，则 BCCD2m，想办法用 m 表示 DF，CF，即可解决问题 （3）如图 2 中，设 CECHn，则 BCCDAB2n，想办法用 n 表示 DF，CF，即可解决问题 【解答
44、】 （1）证明：四边形 ABCD 是正方形， BCDBCH90，CDCB， BGDG， BGEDCE90， BEGCED， CDECBH， DCEBCH（ASA） ， BHDE （2）证明；如图 1 中，设 BEECm，则 BCCD2m， CDECBH， tanCBHtanCDE= 1 2， = 1 2， EG= 5 5 m，BG= 25 5 m，DE= 2+ 2= 5m， CHECm， DHDC+CH3m，DGDE+EG= 65 5 m， GH= 2 2=(3)2 (6 5 5 )2= 35 5 m， ABFH， FHGABG， = ， 2 = 35 5 25 5 ， FH3m， DF6m，CF4m， = 6 4 = 3 2 （3）解：如图 2 中，同法可证，DCEBCH， ECCH， 设 CECHn，则 BCCDAB2n， CDECBH， tanCBHtanCDE= 1 2， = 1 2， GH= 5 5 n，BH= 2+ 2= 5n， GBGH+BH= 65 5 n， FHAB， GFHGAB， = ， 2 = 5 5 65 5 ， FH= 1 3n， DFDHFHn 1 3n= 2 3n，CFCH+FHn+ 1 3n= 4 3n = 2 3 4 3 = 1 2
